1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 83, № 5, 2019

Известия РАН. Серия физическая, 2019, T. 83, № 5, стр. 709-711

Метод устранения суточных вариаций потоков мюонов для матричных наблюдений годоскопа УРАГАН

Р. В. Сидоров 1, *, И. И. Астапов 2, Н. С. Барбашина 2, А. Д. Гвишиани 1, В. Г. Гетманов 1, А. Н. Дмитриева 2, М. Н. Добровольский 1, Д. В. Перегудов 1, А. А. Соловьёв 1, В. Е. Чинкин 1, В. В. Шутенко 2, И. И. Яшин 2

1 Федеральное государственное бюджетное учреждение науки Геофизический центр Российской академии наук
Москва, Россия

2 Федеральное государственное автономное образовательное учреждение высшего образования “Национальный исследовательский ядерный университет “МИФИ”
Москва, Россия

* E-mail: r.sidorov@gcras.ru

Поступила в редакцию 15.09.2018
После доработки 06.11.2018
Принята к публикации 28.01.2019

Полный текст (PDF)

Аннотация

Предложен метод устранения суточных вариаций потоков мюонов для матричных наблюдений годоскопа УРАГАН (НИЯУ МИФИ) на основе матричного цифрового двумерного низкочастотного фильтра. Разработана его структура, основанная на операциях матричных поэлементных умножениях. Реализовано устранение суточных вариаций потоков мюонов для последовательности матриц наблюдений годоскопа УРАГАН.

ВВЕДЕНИЕ И ПОСТАНОВКА ЗАДАЧИ

Потоки мюонов (ПМ), падающие на Землю, подвержены временным и пространственным вариациям, которые можно подразделить на периодические – солнечные 11- и 22-летние и 27‑дневные и суточные от вращения Земли [1] – и на апериодические – от возможных затуханий форбуш-эффекта [2] и воздействий атмосферы [3, 4]. В ряде случаев-вариации могут искажать полезную информацию, содержащуюсяв ПМ. Настоящая статья посвящена разработке метода устранения суточных вариаций ПП для матричных наблюдений мюонного годоскопа (МГ) УРАГАН [5]. В МГ измеряются функции распределения интенсивности ПМ на основе подсчета зарегистрированных мюонов для дискретных телесных углов в течение заданного времени. Измеренные функции распределения размещаются в МГ-матрицах и обозначаются как $Y(i,j,Tn),$ где i = $\overline {1,{{N}_{1}}} ,$ j =  $\overline {1,{{N}_{2}}} ,$ $T$ – шаг по времени, $n = $$\overline {0,{{N}_{f}} - 1} .$ Индексам $i,j$ соответствуют азимутальные и зенитные углы с заданными дискретностями и диапазонами.

Ввиду вращения Земли содержимое МГ-матриц подвержено суточным вариациям с частотой ${{\Omega }_{0}} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}},$ ${{T}_{0}}$ – длительность суток. Здесь определим функцию суммарной интенсивности ПМ $S = S(Tn),\,{\text{м ю о н }} \cdot {{{\text{c}}}^{{ - 1}}},$ в которой устранены атмосферные вариации [6]; вычислим ее дисретное преобразование Фурье (ДПФ) $C(k)$

(1)
$\begin{gathered} S(Tn) = \frac{1}{{{{N}_{1}}{{N}_{2}}}}\sum\limits_{i = 1}^{{{N}_{1}}} {\sum\limits_{j = 1}^{{{N}_{2}}} {Y(i,j,Tn)} } , \\ C(k) = ({1 \mathord{\left/ {\vphantom {1 N}} \right. \kern-0em} N})\sum\limits_{n = 0}^{N - 1} {S(Tn)\exp ({{ - 2\pi nk} \mathord{\left/ {\vphantom {{ - 2\pi nk} N}} \right. \kern-0em} N})} , \\ k = \overline {0,N - 1} . \\ \end{gathered} $

Логарифмический ДПФ-спектр $LC(\Delta Fk)$ = = 20 lg$(C{\text{*}}(k)C(k))$ позволяет оценить амплитуды спектральных составляющих для $S(Tn).$

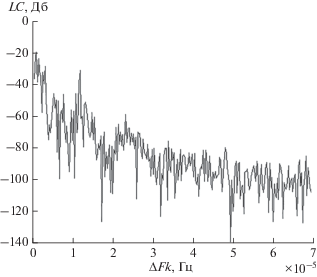
Были рассмотрены наблюдения МГ-матриц, произведенные в течение июня–июля 2015 г., $T = 3600\,с ,$ ${{N}_{f}} = 1451.$ На рис. 1. помещен график $LC,\,\,{\text{Д б }}$ в зависимости от частоты $\Delta Fk,\,\,{\text{Г ц }},$ где $\Delta F = {1 \mathord{\left/ {\vphantom {1 {NT}}} \right. \kern-0em} {NT}}$ – разрешающая способность ДПФ, $N = 1024,$ $\Delta F = 2.7126\,\,{\text{Г ц ,}}$ $k = 0,1,...,260.$ Видны два спектральных пика 1-суточных, 0.5-суточных составляющих с частотами 1.1574 ⋅ 10–5 Гц, 2.3118 ⋅ 10–5 Гц.

Рис. 1.

ДПФ-спектр функции суммарной интенсивности мюонных потоков.

Ставится задача устранения суточных вариаций ПМ для матричных наблюдений $Y(i,j,Tn)$ иформированииматричных последовательностей ${{Y}_{{\text{Ф }}}}(i,j,Tn),$ в которых отсутствовали бы указанные составляющие.

Необходимость устранения вариационных (модуляционных) составляющих в матричных наблюдениях встречается во многих задачах экспериментальной физики, связанных с требованиями разделения разномасштабных по времени процессов; например, при анализе вековых и сезонных процессов льдообразований в полярных областях, при рассмотрении влияния циклической солнечной активности на динамику медленных климатических изменений заданных регионов земной поверхности и т.д.

ДВУХЭТАПНАЯ ДВУМЕРНАЯ НИЗКОЧАСТОТНАЯ ФИЛЬТРАЦИЯ

Для устранения вариаций используем полосовые фильтры. Применим к выходным функциям МГ $Y(i,j,Tn)$ стандартные цифровые одномерные низкочастотные полосовые фильтры с весами ${{b}_{r}}(i,j),\,\,r = 1,...,{{r}_{0}},$ ${{a}_{s}}(i,j),\,\,s = 1,...,{{s}_{0}},$ ${{r}_{0}},{{s}_{0}}$ задают порядок фильтров. Частоты среза фильтров ${{\omega }_{c}}(i,j)$ должны удовлетворять условию ${{\omega }_{c}}(i,j) < {{\Omega }_{0}}.$ Вид фильтра можно взять из комплекса Matlab [9]; запишем его разностное уравнение

(2)
$\begin{gathered} {{Y}_{{\text{ф }}}}(i,j,Tn) = - \sum\limits_{r = 1}^{{{r}_{0}}} {{{b}_{r}}(i,j){{Y}_{{\text{ф }}}}(i,j,T(n - r))} + \\ + \,\,\sum\limits_{s = 0}^{{{s}_{0}}} {{{a}_{s}}(i,j)Y(i,j,T(n - s))} . \\ \end{gathered} $

Использование (2)для поставленной задачи связано с двумя проблемами: 1. Обеспечением малых временных затрат для выполнения ${{N}_{1}}{{N}_{2}}$-операций одномерной фильтрации по (2); 2. Устранением возникающих фазовых сдвигов, которые образуются в ${{Y}_{{\text{Ф }}}}(i,j,Tn)$ в результате фильтрации. Реализуем двухэтапную фильтрацию.

1. Определим матрицы ${{B}_{1}},...,{{B}_{m}},$ ${{A}_{0}},...,{{A}_{k}},$ состоящие из весов (2). На основе (2) сформируем разностное уравнение двумерного фильтра в матричной форме

(3)
$\begin{gathered} {{Y}_{{1{\text{ф }}}}}(Tт ) = - \sum\limits_{r = 1}^{{{r}_{0}}} {{{B}_{r}} \circ {{Y}_{{1{\text{ф }}}}}(T(т - r))} + \\ + \,\,\sum\limits_{s = 0}^{{{s}_{0}}} {{{A}_{s}} \circ Y(T(т - s))} , \\ \end{gathered} $
где “$ \circ $” обозначает операцию поэлементного умножения матриц. С использованием [9] реализуется быстрое поэлементное умножение.

2. Произведем устранение фазовых сдвигов. Введем по аналогии с (1) функцию суммарной интенсивности ${{S}_{{1{\text{ф }}}}}(Tn)$ для ${{Y}_{{1{\text{ф }}}}}(i,j,Tn).$ Сформируем функционал $F(S,{{S}_{{\text{ф }}}},{{n}_{d}}),$ найдем оптимальный фазовый сдвиг $n_{d}^{ \circ }$

(4)
$\begin{gathered} {{S}_{{1{\text{ф }}}}}(Tn) = \frac{1}{{{{N}_{1}}{{N}_{2}}}}\sum\limits_{i = 1}^{{{N}_{1}}} {\sum\limits_{j = 1}^{{{N}_{2}}} {{{Y}_{{1{\text{ф }}}}}(i,j,Tn)} } , \\ F(S,{{S}_{{1{\text{ф }}}}},{{n}_{d}}) = \sum\limits_{n = {{n}_{1}}}^{{{n}_{2}}} {(S(Tn) - {{S}_{{1{\text{ф }}}}}{{{(T(n - {{n}_{d}}))}}^{2}}} , \\ n_{d}^{ \circ } = \arg \left\{ {\mathop {\min }\limits_{1 \leqslant {{n}_{d}} \leqslant {{n}_{{d0}}}} F(S,{{S}_{{1{\text{ф }}}}},{{n}_{d}})} \right\}. \\ \end{gathered} $

Результат фильтрации определим как Yф(i, j, Tn) = = ${{Y}_{{1{\text{ф }}}}}\left( {i,j,T\left( {n - n_{d}^{ \circ }} \right)} \right).$

УСТРАНЕНИЕ СУТОЧНЫХ ВАРИАЦИЙ В МЮОННЫХ ПОТОКАХ ДЛЯ НАБЛЮДЕНИЙ ГОДОСКОПА УРАГАН

1. Были вычислены МГ-матрицы ${{Y}_{{1{\text{ф }}}}}(Tn)$ с помощью одномерных фильтров Баттерворта порядка ${{N}_{{\text{B}}}} = 8;$ на их основе были сформированы функции ${{Y}_{{1{\text{ф }}}}}(i,j,Tn)$ с фазовыми сдвигами. На рис. 2 кривая 1 соответствует функции cуммарной интенсивности $S = S(Tn)$ для МГ в зависимости от времени $Tn,с ,$ ${{\bar {n}}_{1}} \leqslant n \leqslant {{\bar {n}}_{2}},$ ${{\bar {n}}_{1}} = 200,$ ${{\bar {n}}_{2}} = 1451;$ видны суточные вариации с амплитудой ≈0.0015, среднее значение интенсивности ≈0.2; кривая 2 представляет собой график с фазовым сдвигом. В кривой 2 отсутствуют суточные вариации. С применением оптимизации $F(S,{{S}_{{\text{Ф }}}},{{n}_{d}})$ была найдена оценка фазового сдвига $n_{d}^{ \circ } = 39.$

Рис. 2.

Результаты работы двумерного матричного фильтра для устранения суточных вариаций мюонных потоков.

2. Проведенные вычислительные эксперименты позволили установить, что временные затраты предложенного метода двумерной фильтрации в среднем на порядок меньше временных затрат, которые реализуются для фильтрации на основе одномерных фильтров; погрешности оценки фазовых сдвигов составляют величины порядка 1°‒2°; амплитуды модельных синусоидальных вариаций снижаются в $ \approx {\kern 1pt} 10{\kern 1pt} - {\kern 1pt} 20$ раз.

Разработанная в статье матричная фильтрация по сравнению с традиционной [7, 8] является более эффективной в части временных затрат и устранения фазовых сдвигов.

ЗАКЛЮЧЕНИЕ

1. Предложенный метод устранения суточных вариаций потоков мюонов для матричных наблюдений годоскопа УРАГАН на основе матричного цифрового двумерного низкочастотного фильтра оказался работоспособным.

2. Установлено на основе вычислительных экспериментов, что временные затраты предложенного метода фильтрации в среднем на порядок меньше временных затрат, которые реализуются для фильтрации на основе одномерных фильтров; погрешности оценивания фазовых сдвигов составляют величины порядка $1^\circ {\kern 1pt} - {\kern 1pt} 2^\circ ;$ амплитуды модельных синусоидальных вариаций снижаются в $ \approx {\kern 1pt} 10{\kern 1pt} - {\kern 1pt} 20$ раз.

3. Предложенный метод может быть применен для многих задач экспериментальной физики, связанных с устранением в последовательностях матричных данных составляющих периодических вариаций (модуляций).

Работа выполнена при поддержке гранта Российского научного фонда № 17-17-01215.

Список литературы

  1. Poirier J., Catanach T. // 32-nd Intern. Cosmic Ray Conf. Beuiing. 2011. V. 11. P. 173.

  2. Braun I., Engler J., Horandel J.R. et al. // Adv. Space Res. 2009. V. 43. P. 480.

  3. Karapetyan G.G. // Phys. Rev. D. 2014. V. 89. Art. no. 093005.

  4. Dmitrieva A.N., Kokoulin R.P., Petrukhin A.A. et al. // Astropart. Phys. 2011. V. 34. P. 401.

  5. Yashin I.I., Astapov I.I., Barbashina N.S. et al. // Adv. Space Res. 2015. V. 56. № 12. P. 2693.

  6. Dmitrieva A., Anpilogov N., Astapov I. et al. // J. Phys. Conf. Ser. 2015. V. 632. Art. no. 012054.

  7. Two-dimensional Signal Analysis. Ed. R. Garello. J. Wiley-ISTE. 2013. 352 p.

  8. Дьяконов В.П., Абраменкова И.В. Matlab. Обработка сигналов и изображений. СПб.: Питер, 2002. 608 с.

  9. http://matlab.exponenta.ru/imageprocess.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал