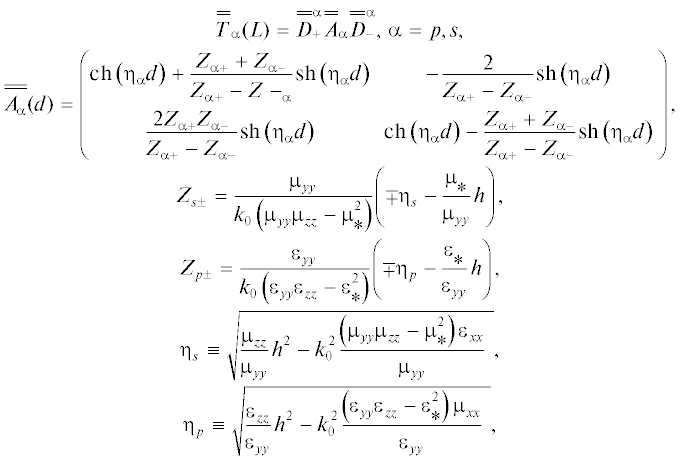Известия РАН. Серия физическая, 2019, T. 83, № 6, стр. 769-772

Постоянно растущие требования к миниатюризации оптоэлектронных устройств стимулируют неснижающийся интерес к изучению эффектов незеркального отражения и прохождения – отклонений в структуре волнового поля (по отношению к предсказываемым геометрической оптикой для монохроматической плоской волны), возникающих при падении квазиплоской волны ТМ- или ТЕ-типа на слоистую оптически прозрачную структуру. Подобные отклонения возникают уже в условиях полного внутреннего отражения (ПВО) для остронаправленного волнового пучка, падающего из оптически более плотной среды на уединенную границу раздела оптически прозрачных диэлектриков [1]. Для волны ТМ- или ТЕ-типа такое отклонение представляет собой продольное смещение отраженного пучка вдоль линии пересечения плоскости падения и плоскости границы раздела сред (пространственный эффект Гуса–Хенхен [2, 3]). Если же падение квазиплоской волны в условиях ПВО происходит на поверхность не полупространства, а оптически прозрачного слоя, то, вследствие неполного отражения (нарушенное ПВО), пространственный эффект Гуса–Хенхен может иметь место не только для отраженной, но также и для прошедшей через слой квазиплоской волны. Одновременно с этим, в плоскости падения пучка направление оси как отраженной, так и прошедшей через слой квазиплоской волны, по сравнению с геометрической оптикой также может изменять свое направление (на величину, обратно пропорциональную квадрату ширины падающего на слой гауссова волнового пучка), что отвечает угловому эффекту Гуса–Хенхен [1]. Анализ подобных оптических аномалий безусловно представляет не только чисто академический, но и несомненный практический интерес. При этом, несмотря на интенсивные исследования, в подавляющем числе работ, связанных с этой темой, традиционно рассматривается исключительно случай наклонного падения пучка. Однако в работе [4] теоретически была продемонстрирована принципиальная возможность формирования в условиях ПВО пространственного эффекта Гуса–Хенхен для случая нормального падения пучка объемных волн ТЕ-типа на уединенную поверхность оптически прозрачной среды при условии, что она обладает гиротропией (собственной или вынужденной). В качестве примера была рассмотрена двухподрешеточная модель легкоосного одноосного антиферромагнетика в случае, когда равновесное направление вектора магнитной индукции ${{\vec {B}}_{0}}$ одновременно ортогонально как сагиттальной плоскости, так и легкой магнитной оси, лежащей в плоскости падения (геометрия Фогта). В этом случае удобно, представить френелевские коэффициенты прохождения ${{W}_{\alpha }}$ и отражения ${{R}_{\alpha }}$ соответственно как ${{W}_{\alpha }} = \exp \left[ {\ln {{W}_{\alpha }}} \right]$ и ${{R}_{\alpha }} = \exp \left[ {\ln {{R}_{\alpha }}} \right]$ и, следуя стандартной процедуре расчета, разложить показатель экспоненты в ряд по $h,$ ограничиваясь степенями не выше первой ($h$ – поперечное волновое число, $\omega $ – частота). В результате в условиях нормального падения квазиплоской волны ТМ-или ТЕ-типа на поверхность слоя в рамках метода стационарной фазы получается следующая связь для ${{\Delta }_{{r\alpha }}},$ ${{s}_{{r\alpha }}}$(эффекты незеркальности первого порядка при отражении) и ${{R}_{\alpha }} = \left| {{{R}_{\alpha }}} \right|\exp \left[ {i{{\varphi }_{\alpha }}} \right]$ на входной поверхности слоя

В этих же условиях аналогичный расчет приводит к следующим соотношениям между ${{\Delta }_{{t\alpha }}},$ ${{s}_{{t\alpha }}}$ (эффекты незеркальности первого порядка при прохождении (туннелировании)) и ${{W}_{\alpha }} = \left| {{{W}_{\alpha }}} \right|\exp \left[ {i{{\psi }_{\alpha }}} \right]$ на выходной поверхности слоя

Из (1), (2), в частности, следует, что в случае нормального падения из вакуума на слой оптически прозрачного изотропного диэлектрика ($h = 0$) квазиплоской волны с $\alpha = p,s$ и пространственный и угловой эффекты Гуса–Хенхен отсутствуют как для отраженной (${{\Delta }_{{r\alpha }}} = {{s}_{{r\alpha }}} = 0$), так и для прошедшей через слой квазиплоской волны (${{\Delta }_{{t\alpha }}} = {{s}_{{t\alpha }}} = 0$) и ТМ-, и ТЕ-типа. Однако, как следует из [4], при $\left. {{{{\vec {B}}}_{0}}\,} \right\|\vec {a}$ ($\vec {a}$ – нормаль к плоскости падения) одновременно ${{\Delta }_{{r\alpha }}} \ne 0,{{s}_{{r\alpha }}} = 0$ и ${{\Delta }_{{t\alpha }}} = {{s}_{{t\alpha }}} = 0$ при $\alpha = p,s$ [4]. В [5] было показано, что полученные в [4] результаты остаются справедливыми и в случае нормального падения квазиплоской волны ТЕ-типа на касательно намагниченный слой ферромагнетика в геометрии Фогта. При этом расчеты, выполненные в [4, 5], содержали существенное с точки зрения целей нашей работы ограничение: среда, спектр нормальных объемных магнитных поляритонов слоя не зависел от инверсии знака направления распространения волны в плоскости слоя ($h \to - h$).

В данной работе с помощью метода стационарной фазы показано, что в геометрии Фогта невзаимность спектра нормальных магнитных поляритонов неограниченного одномерного магнитного фотонного крнсталла (1D МФК) относительно инверсии направления распространения в плоскости слоев может приводить к незеркальным эффектам первого порядка (пространственному и угловому эффектам Гуса–Хенхен ) как при отражении, так и прохождении (туннелировании ) квазиплоской воны ТМ- (ТЕ-)типа, нормально падающей на поверхность конечного оптически прозрачного 1D МФК, находящегося в вакууме.

В дальнейшем ограничимся случаем, когда уравнения связи всех рассматриваемых сред, формирующих 1D МФК, для выбранной геометрии распространения без учета граничных условий допускают при заданных значениях частоты $\omega $ и продольного волнового числа $h$ независимое распространение волн ТМ- и ТЕ-типа. Волновые свойства контактирующих сред будем характеризовать с помощью соотношений

Здесь, согласно [6], введены поверхностный волновой импеданс ${\text{ }}Z_{p}^{{}}$ (в случае волны ТМ-типа) и поверхностная волновая проводимость $Z_{s}^{{}}$ (для волны ТЕ-типа). Вектор $\vec {b}$ лежит вдоль линии пересечения плоскости границы раздела сред и сагиттальной плоскости ($\vec {a} = \left[ {\vec {b}\vec {q}} \right],$ $\vec {q}$ – нормаль к поверхности 1D МФК). В частности для вакуума ${{\tilde {Z}}_{p}}{\text{ }} = {{\sqrt {\tilde {\varepsilon }k_{{\text{0}}}^{{\text{2}}} - h_{{}}^{{\text{2}}}} } \mathord{\left/ {\vphantom {{\sqrt {\tilde {\varepsilon }k_{{\text{0}}}^{{\text{2}}} - h_{{}}^{{\text{2}}}} } {\left( {\tilde {\varepsilon }k_{{\text{0}}}^{{}}} \right)}}} \right. \kern-0em} {\left( {\tilde {\varepsilon }k_{{\text{0}}}^{{}}} \right)}},$ ${{\tilde {Z}}_{s}}{\text{ }} = {{\sqrt {\tilde {\varepsilon }k_{{\text{0}}}^{{\text{2}}} - h_{{}}^{{\text{2}}}} } \mathord{\left/ {\vphantom {{\sqrt {\tilde {\varepsilon }k_{{\text{0}}}^{{\text{2}}} - h_{{}}^{{\text{2}}}} } {k_{{\text{0}}}^{{}}}}} \right. \kern-0em} {k_{{\text{0}}}^{{}}}}$ (${{k}_{0}} \equiv {\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0em} c},$ $c$ – скорость света). Для рассматриваемого в данной работе случая независимого распространения в выбранной сагиттальной плоскости волн ТМ- и ТЕ-типа трансфер-матрица ${{\overline{\overline T} }_{\alpha }}\left( {\omega ,h} \right),$ связывающая значения касательных к границе раздела слоев компонент векторов магнитного и электрического поля, в зависимости от поляризации волны $\alpha = p$ или $\alpha = s$ для находящегося в вакууме конечного одномерного фотонного кристалла (1D МФК), состоящего из $N$ элементарных периодов, может быть представлена в виде:

В дальнейшем ограничимся анализом случая 1D МФК, элементарный период которого образован касательно намагниченным ферромагнитным (геометрия Фогта) слоем толщиной $d$ и матрицей перехода ${{\overline{\overline A} }_{\alpha }}\left( {\omega ,h} \right),$ разделяющим два окружающих его негиротропных, оптически изотропных, неидентичных слоя с матрицами перехода $\overline{\overline D} _{ + }^{\alpha }$ и $\overline{\overline D} _{ - }^{\alpha }$ и толщинами ${{d}_{ + }}$ и $d,$, соответственно. В этом случае трансфер-матрица ${{\overline{\overline T} }_{\alpha }}\left( {\omega ,h} \right)$ в (4) определяется как

где ${{Z}_{{\alpha + }}}$ и ${{Z}_{{\alpha - }}}$ – поверхностные импедансы (адмиттансы) нормальной поляритонной волны поляризации $\alpha = p$ и $\alpha = s$ соответственно на верхней (“+”) и нижней (“–”) границе гиротропного слоя, $\eta _{{\alpha \nu }}^{{}}$ – обратная глубина проникновения волны в диэлектрик $\nu $ ($\nu = \pm $), $Z_{{\alpha \nu }}^{{}}$ – поверхностный импеданс немагнитной диэлектрической среды $\nu .$

В результате, с учетом максвелловских граничных условий, структура френелевских коэффициентов отражения ${{R}_{\alpha }}$ и прохождения ${{W}_{\alpha }}$ в случае конечного 1D МФК из $N$ элементарных периодов с учетом (4)–(6) имеет следующую структуру

Как показано в [7], спектр нормальных магнитных поляритонов как ТМ-, так и ТЕ-типа такого неограниченного 1D МФК является невзаимным относительно инверсии знака волнового вектора в плоскости границы раздела ($h \to - h$) слоев: ${{\chi }_{\alpha }}(h) \ne {{\chi }_{\alpha }}( - h).$ С учетом (1) и (2) и (4)–(7) это приводит к тому, что при прохождении через слой такого 1D МФК остронаправленного пучка волн ТМ- или ТЕ-типа формируются незеркальные эффекты первого порядка не только в случае наклонного, но уже и в случае нормально падающего волнового пучка. В частности это выражается в появлении, в отличие от [4, 5], углового эффекта Гуса–Хенхен как для отраженной, так и для прошедшей через ограниченный 1D МФК квазиплоской электромагнитной волны ТМ- или ТЕ-типа, а также пространственного эффекта Гуса–Хенхен для остронаправленного волнового пучка, прошедшего через слой. Их формирование связано с возбуждением в слое вытекающей объемной или эванесцентной волны соответствующей поляризации с равным нулю продольным волновым числом $h$ и отличным от нуля интегральным потоком энергии вдоль плоскости слоя. При этом величина и знак указанных эффектов тесно связаны с асимметрией поляритонного спектра и в частности с гиротропными свойствами ферромагнитного слоя. Это дает возможность управления не только величиной, но и знаком указанных незеркальных эффектов прохождения с помощью изменения не только величины и направления приложенного внешнего магнитного поля (${{\vec {B}}_{0}}||\vec {a}$), но и за счет изменения толщины и относительного расположения магнитных и немагнитных слоев, образующих элементарный период рассматриваемого 1D МФК. При этом во всех отмеченных выше магнитооптических конфигурациях, отвечающих (4)–(6), в условиях наклонного падения (h = k₀sin θ)

Отметим, что для геометрии Фогта одновременное отличие от нуля ${{\Delta }_{{t\alpha }}}(h = 0),$ ${{s}_{{r\alpha }}}(h = 0)$ и ${{s}_{{t\alpha }}}(h = 0)$ возможно также и при нормальном падении квазиплоской волны ТМ- или ТЕ-типа на негиротропный одномерный ФК с касательно намагниченным гиротропным дефектным слоем, асимметрично расположенным относительно срединной плоскости такой одномерной сверхрешетки (например, на поверхности конечного негиротропного 1D ФК). Если такая структура находится в вакууме, то с учетом (4)–(6)

а значит, при P₁ ≠ P₂ одновременно Δ_tα(h = 0), ${{\Delta }_{{r\alpha }}}(h = 0) \ne 0$ и ${{s}_{{t\alpha }}}(h = 0),$ ${{s}_{{r\alpha }}}(h = 0) \ne 0.$

Таким образом, для геометрии Фогта становится возможным одновременное формирование не только пространственного эффект Гуса–Хенхен при прохождении, но также углового эффекта Гуса–Хенхен (как при отражении, так и при прохождении) для квазиплоской волны ТМ- или ТЕ-типа, нормально падающей извне на поверхность ограниченного 1D МФК, поляритонный спектр которого является невзаимным вследствие одновременного нарушения в такой слоистой структуре как зеркальной симметрии, так и пространственно-временной инверсии. Подчеркнем, что наличие элементарной ячейки в виде гиротропного слоя в асимметричном окружении не является необходимым условием для формирования указанных незеркальных эффектов первого порядка для квазиплоской волны ТМ- или ТЕ-типа, нормально падающей на ограниченный 1D МФК. В частности, аналогичные эффекты могут быть реализованы и в негиротропном 1D МФК типа “немагнитный диэлектрик–магнетик с антисимметричным магнитоэлектрическим взаимодействием”, а также в двухкомпонентном 1D МФК на основе гиротропных слоев (геометрия Фогта).