Известия РАН. Серия физическая, 2019, T. 83, № 9, стр. 1273-1276
Многочастичные взаимодействия в ядерной материи
Е. Г. Друкарев 1, М. Г. Рыскин 1, В. А. Садовникова 1, *
1 Федеральное государственное бюджетное учреждение “Петербургский институт ядерной физики
имени Б.П. Константинова Национального исследовательского центра “Курчатовский институт”
Гатчина, Россия
* E-mail: sadovnik@thd.pnpi.spb.ru
Поступила в редакцию 12.11.2018
После доработки 08.04.2019
Принята к публикации 27.05.2019
Аннотация
Исследовано влияние трехнуклонных и четырехнуклонных сил на характеристики нуклона в симметричной ядерной материи с использованием метода правил сумм при конечной плотности. Подход, в рамках которого материя рассматривается как система нуклонов в “пионных шубах” (т.е. однопионные и итерированные однопионные обмены включаются в описание одночастичных состояний), позволяет получить строгую иерархию многочастичных сил.
ВВЕДЕНИЕ
В этой работе мы продолжаем изложение наших результатов по исследованию многочастичных взаимодействий в ядерной материи. Используется метод правил сумм квантовой хромодинамики (КХД) при конечной плотности, основы которого описаны в обзоре [1] (о правилах сумм КХД в вакууме см. книгу [2]). В нашей предыдущей работе [3] мы приводим основные формулы, используемые при вычислениях. Напомним только, что метод основан на дисперсионных соотношениях для поляризационного оператора, описывающего распространение системы с квантовыми числами протона. В правой части дисперсионных соотношений мы выделяем нуклонный (протонный) полюс, соответствующий пробному нуклону, а высшие реальные состояния описываем континуумом с эффективным порогом $W_{m}^{2}.$ Параметры нуклона в материи: эффективная масса $m{\text{*}}$ и векторная собственная энергия ${{\Sigma }_{V}}$ являются решением системы уравнений.
(1)
$\frac{{{{\mathcal{L}}^{I}}({{M}^{2}},W_{m}^{2})}}{{{{\mathcal{L}}^{q}}({{M}^{2}},W_{m}^{2})}} = m*;\,\,\,\,\frac{{{{\mathcal{L}}^{P}}({{M}^{2}},W_{m}^{2})}}{{{{\mathcal{L}}^{q}}({{M}^{2}},W_{m}^{2})}} = - \frac{{{{\Sigma }_{V}}}}{m},$Функции ${{\mathcal{L}}^{i}}$ зависят от средних значений операторов КХД в ядерной материи, называемых конденсатами. Зная зависимость параметров конденсата от плотности среды $\rho ,$ мы можем, таким образом, найти зависимость от плотности характеристик пробного нуклона. Как и в случае вакуума, предполагается, что роль конденсатов уменьшается с увеличением их размерности. Поэтому наиболее важны векторный и скалярный конденсаты ${\nu }({\rho }) = \left\langle {M\left| {\sum\nolimits_i {{{{\bar {q}}}^{i}}} {{{\gamma }}_{0}}{{q}^{i}}} \right|M} \right\rangle $ и ${\kappa }({\rho }) = \left\langle {M\left| {\sum\nolimits_i {{{{\bar {q}}}^{i}}} {{q}^{i}}} \right|M} \right\rangle .$ Здесь ${{q}^{i}}$ – кварковые операторы, индекс i соответствует u и d кваркам, $\left| M \right\rangle $ – основное состояние материи. Векторный конденсат записан в системе покоя материи.
Пока мы ограничиваемся конденсатами с d = 3, структуры ${{\mathcal{L}}^{q}}$ и ${{\mathcal{L}}^{P}}$ зависят от векторного конденсата и не зависят от ${\kappa }(\rho ).$ В свою очередь ${{\mathcal{L}}^{I}}$ зависит только от скалярного конденсата. Если пренебречь малым отличием величины порога $W_{m}^{2}$ от вакуумного значения $W_{0}^{2}$ [4], то два уравнения (1) становятся независимыми. В этом приближении векторная собственная энергия ${{\Sigma }_{V}}$ не зависит от скалярного конденсата ${\kappa }(\rho ).$ Поэтому в точном решении мы ожидаем слабой зависимости ${{\Sigma }_{V}}$ от скалярного конденсата, в то время как эффективная масса $m{\text{*}}$ почти полностью им определяется.
Векторный конденсат легко вычисляется: ν(q) = = ${{n}_{{\text{v}}}}{\rho ,}$ где ${{n}_{{\text{v}}}}$ – число валентных кварков в нуклоне (${{n}_{{\text{v}}}}$ = 3). Однако нахождение скалярного конденсата требует модельных представлений для $\left| M \right\rangle .$ Построению такой модели и посвящена настоящая работа.
1. НУКЛОНЫ В “ПИОННЫХ ШУБАХ”
В качестве первого шага состояние $\left| M \right\rangle $ обычно представляют как систему нерелятивистских невзаимодействующих нуклонов (газовое приближение). В этом случае отличие скалярного конденсата от вакуумного значения ${\kappa }(0)$ определяется суммой вкладов отдельных нуклонов ${{{\kappa }}_{N}} = \left\langle {N\left| {\sum\nolimits_i {{{{\bar {q}}}^{i}}} {{q}^{i}}} \right|N} \right\rangle ,$ где $\left| N \right\rangle $ – вектор состояния свободного покоящегося нуклона. Этот матричный элемент просто выражается через нуклонный сигма-член ${{{\sigma }}_{N}},$ связанный с наблюдаемыми. Таким образом,
(2)
$\begin{gathered} {\kappa }({\rho }) = {\kappa }(0) + {{{\kappa }}_{N}}{\rho }; \\ {{{\kappa }}_{N}} = \left\langle {N\left| {\sum\limits_i {\bar {q}} q} \right|N} \right\rangle = \frac{{2{{{\sigma }}_{N}}}}{{{{m}_{u}} + {{m}_{d}}}}, \\ \end{gathered} $На следующем этапе мы учитываем взаимодействие нуклонов в состоянии $\left| M \right\rangle ,$ предполагая, что оно происходит путем обмена мезонами. Нам нужно учесть вклад общего мезонного облака в конденсат ${\kappa }({\rho })$. Основная часть вклада определяется пионами [1]. Это связано с тем, что при разумных предположениях о виде кварковой волновой функции матричный элемент $\left\langle {h\left| {\sum\nolimits_i {\bar {q}} q} \right|h} \right\rangle $ представляет собой суммарное число кварков и антикварков ${{n}_{{\bar {q}q}}}$ в адроне h. Поэтому для мезонов следует ожидать ${{n}_{{\bar {q}q}}}$ = 2, в то время как для пионов ${{n}_{{\bar {q}q}}} = {{{{m}_{{\pi }}}} \mathord{\left/ {\vphantom {{{{m}_{{\pi }}}} {({{m}_{u}} + {{m}_{d}})}}} \right. \kern-0em} {({{m}_{u}} + {{m}_{d}})}} \approx 12,$ что объясняется большим числом “морских” кварк-антикварковых пар.
Таким образом, нужно учесть вклад пионных взаимодействий в вектор состояния $\left| M \right\rangle .$ Учету двухчастичных взаимодействий будет соответствовать учет трехчастичных взаимодействий в характеристиках пробного нуклона $m{\text{*}}$ и ${{\Sigma }_{V}}.$ Включение трехчастичных взаимодействий в состоянии $\left| M \right\rangle $ приведет к учету четырехчастичных взаимодействий в характеристиках нуклонов, и т.д. Вклады однопионного и двухпионных взаимодействий в скалярный конденсат вычислены в [5] c использованием киральной теории возмущений.
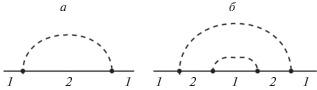
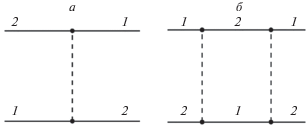
Заметим, что интерпретация однопионного взаимодействия не является однозначной. Обмен пионами между нуклонами среды с трехмерными импульсами ${{p}_{1}}$ и ${{p}_{2}}$ выражается фейнмановской диаграммой, изображенной на рис. 1а. Только обменный (фоковский) член дает ненулевой вклад. Прямой (хартриевский) член равен нулю, так как пион-нуклонная вершина пропорциональна импульсу, передаваемому пионом. Обычно этот вклад включается в двухчастичное взаимодействие. Однако он может быть представлен как собственная энергия нуклона в среде (см. рис. 2а). Диаграмма, изображенная на рис. 2а с интегрированием по трехмерному импульсу промежуточного нуклона ${{p}_{2}}$ от 0 до ∞, уже учтена в одночастичной функции нуклона с импульсом ${{p}_{1}}$. Однако в среде состояния с импульсами ${{p}_{2}} < {{p}_{F}},$ где ${{p}_{F}}$ $ - $ импульс Ферми, заняты, и этот вклад необходимо вычесть. Интеграл по энергиям может быть выражен через вычет в полюсе нуклонного пропагатора, и вклад диаграммы рис. 2б соответствует диаграмме рис. 1а, просуммированной по всем импульсам ${{p}_{2}} < {{p}_{F}}.$ То же относится к итерированному однопионному обмену, описываемому диаграммой рис. 1б [6]. Ему соответствует диаграмма собственной энергии, изображенная на рис. 2б.
Рис. 1.
Фейнмановские диаграммы, описывающие однопионный (а) и итерированный однопионный (б) обмены между нуклонами материи 1 и 2. Сплошные линии соответствуют нуклонам, пунктирные $ - $ пионам.
Если пренебречь всеми взаимодействиями, кроме однопионного и итерированного однопионного обменов, то получится система невзаимодействующих нуклонов, каждый из которых обладает своей “пионной шубой” (“квазисвободные нуклоны”). Для такой системы можно написать аналог формулы (2)
где(4)
${\hat {\kappa }(\rho )} = {{{\kappa }}_{{\text{N}}}}{\rho } + {{{\kappa }}^{{{\text{(1)}}}}};\,\,\,\,{{{\kappa }}^{{(1)}}} = \left\langle {{\pi }\left| {\sum\limits_i {\bar {q}} q} \right|{\pi }} \right\rangle {{f}^{{(1)}}}({\rho }).$Среднее значение по пиону обычно записывают как $\left\langle {{\pi }\left| {\sum\nolimits_i { \bar {q}q} } \right|{\pi }} \right\rangle $ = ${{2{{m}_{{\pi }}}{{m}_{{\pi }}}} \mathord{\left/ {\vphantom {{2{{m}_{{\pi }}}{{m}_{{\pi }}}} {({{m}_{u}} + {{m}_{d}}),}}} \right. \kern-0em} {({{m}_{u}} + {{m}_{d}}),}}$ где ${{m}_{{\pi }}}$ – масса пиона. Множитель $2{{m}_{{\pi }}}$ получается в результате выделения нормировочных факторов ${{\left( {2{{m}_{{\pi }}}} \right)}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ в векторах состояний пионов. Функция ${{f}^{{(1)}}}({\rho })$ может быть найдена как производная по $m_{{\pi }}^{2}$ суммы плотностей энергий однопионного и итерированного однопионного обменов [5]. Последнее утверждение иллюстрируется диаграммой рис. 3. Более строгое доказательство основано на теореме Гельмана–Фейнмана (Hellman–Feynman).
Появление “пионной шубы” заметно меняет величину ${{{\kappa }}_{N}}({\rho }).$ Так, при ${{{\sigma }}_{N}}$ = 45 МэВ находим ${{{\kappa }}_{N}} = 8.2.$ Записав 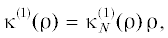 при феноменологическом значении равновесной плотности ${{{\rho }}_{0}} = 0.17 {\text{ф}}{{{\text{м}}}^{{ - 3}}}$ получаем
при феноменологическом значении равновесной плотности ${{{\rho }}_{0}} = 0.17 {\text{ф}}{{{\text{м}}}^{{ - 3}}}$ получаем 
Рис. 3.
Фейнмановская диаграмма, иллюстрирующая на примере однопионного обмена формулу (4). Жирные линии обозначают оператор $\bar {q}q.$ Остальные обозначения такие же, как на рис. 1, 2.

Скалярный конденсат с учетом двухчастичных (2N) взаимодействий в состоянии $\left| M \right\rangle $ в нашем представлении
(5)
$\begin{gathered} {\hat {\kappa }}({\rho }) = {{{\kappa }}_{N}}{\rho } + {{{\kappa }}^{{(1)}}} + {{{\kappa }}^{{(2)}}}; \\ {{{\kappa }}^{{(2)}}} = \left\langle {{\pi }\left| {\sum\limits_i {\bar {q}} q} \right|{\pi }} \right\rangle {{f}^{{(2)}}}({\rho }), \\ \end{gathered} $Правила сумм с таким конденсатом определяют характеристики пробного нуклона с учетом 4N сил.
Отметим, что в обычном (стандартном) представлении при учете многочастичных сил несколько механизмов дают большие, частично компенсирующиеся вклады в скалярный конденсат. В нашем представлении можно выделить один ведущий вклад $ - $ двухпионный обмен, содержащий $\Delta $ – изобару в промежуточном состоянии.
2. РЕЗУЛЬТАТЫ
Записав ${\kappa }({\rho }) = {\kappa }(0)$ + $(\kappa _{N}^{{(1)}}({\rho })$ + $\kappa _{N}^{{(2)}}({\rho })$ + + $\kappa _{N}^{{(3)}}({\rho })) {\rho ,}$ где второе и третье слагаемые в скобках соответствуют учету 2N и 3N взаимодействий в состоянии $\left| M \right\rangle ,$ найдем, что $\kappa _{N}^{{(1)}}({\rho }) > \kappa _{N}^{{(2)}}({\rho }) > \kappa _{N}^{{(3)}}({\rho }).$ Так как эффективная масса определяется в основном скалярным конденсатом, ожидаем получить строгую иерархию вкладов многочастичных сил в $m{\text{*}}.$ Векторная собственная энергия определяется в основном векторным конденсатом. Вклад в многочастичные силы дают также конфигурации четырехкварковых конденсатов (d = 6), в которых две пары кварковых операторов действуют на два разных нуклона среды. При этом скалярно-скалярный конденсат, пропорциональный ${{{\hat {\kappa }}}^{2}},$ дает вклад в структуру ${{\mathcal{L}}^{q}},$ непосредственно влияя на величину ${{\Sigma }_{V}}.$ Таким образом, мы предполагаем получить строгую иерархию и для вкладов в ${{\Sigma }_{V}}.$
Непосредственный расчет подтверждает эти оценки. Для ${\rho } = {{{\rho }}_{0}}$ мы получаем $m{\text{*}}$ = 433 МэВ при учете только 2N сил. Таким образом, ΣS = = $m{\text{*}} - m \approx - 500$ МэВ, отличаясь почти на 150 МэВ от величины, получаемой в обычном представлении. Трехчастичные силы прибавляют к этой величине 174 МэВ, а 4N силы – еще 24 МэВ. Векторная собственная энергия ${{\Sigma }_{V}}$ = 207 МэВ при учете только 2N сил. Учет 3N сил уменьшает векторную собственную энергию на 24 МэВ, а включение 4N сил увеличивает на 11 МэВ.
На рис. 4 приведена зависимость от плотности нуклонных параметров. Здесь же показана одночастичная потенциальная энергия $U = {{\Sigma }_{S}} + {{\Sigma }_{V}}$ = = $m{\text{*}} + {{\Sigma }_{V}} - m.$ Более детально вблизи равновесной плотности ${{{\rho }}_{0}}$ эта зависимость приведена в табл. 1.
Рис. 4.
Зависимость от плотности эффективной нуклонной массы $m*,$ векторной собственной энергии ${{\Sigma }_{V}}$ и одночастичного потенцияла U. На горизонтальной оси отложено отношение плотности материи ${\rho }$ к равновесной плотности ${{{\rho }}_{0}}.$ Точечные кривые $ - $ расчет с учетом двухчастичных взаимодействий нуклонов материи; штриховые кривые $ - $ с учетом 2N и 3N взаимодействий; сплошные кривые $ - $ с учетом 2N, 3N и 4N взаимодействий.
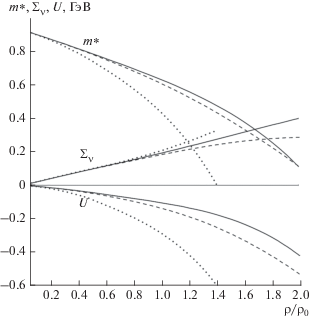
Таблица 1.
Зависимость нуклонных характеристик от плотности. Для каждого значения ${{\rho } \mathord{\left/ {\vphantom {{\rho } {{{{\rho }}_{0}}}}} \right. \kern-0em} {{{{\rho }}_{0}}}}$ верхняя строка показывает параметры пробного нуклона в системе нуклонов, одетых “пионными шубами” с учетом только 2N сил. Вторая и третья строка соответствуют учету 3N и 4N сил
| ${{\rho } \mathord{\left/ {\vphantom {{\rho } {{{{\rho }}_{0}}}}} \right. \kern-0em} {{{{\rho }}_{0}}}}$ | $m*,$ МэВ | ${{\Sigma }_{V}},$ МэВ | U, МэВ |
|---|---|---|---|
| 0.90 | 509 | 182 | —237 |
| 646 | 167 | —116 | |
| 664 | 173 | —92 | |
| 0.95 | 472 | 195 | —262 |
| 627 | 175 | —127 | |
| 648 | 182 | —98 | |
| 1.00 | 433 | 207 | —288 |
| 607 | 183 | —138 | |
| 631 | 192 | —105 | |
| 1.05 | 392 | 221 | —316 |
| 587 | 191 | —150 | |
| 613 | 202 | —112 | |
| 1.10 | 347 | 235 | —347 |
| 567 | 199 | —162 | |
| 595 | 212 | —129 |
Список литературы
Drukarev E.G., Ryskin M.G., Sadovnikova V.A. // ЯФ. 2011. T. 74. C. 1; Drukarev E.G., Ryskin M.G., Sadovnikova V.A. // Phys. Atom. Nucl. 2012. V. 75. P. 334.
Ioffe B.L., Lipatov L.N., Fadin V.S. Quantum chromodynamics. Cambridge: Cambridge Univ. Press, 2010. 596 p.
Друкарев Е.Г., Рыскин М.Г., Садовникова В.А. // Изв. РАН. Cер. физ. 2017. Т. 81. С. 1334; Drukarev E.G., Ryskin M.G., Sadovnikova V.A. // Bull. Russ. Acad. Sci. Phys. 2017. V. 81. P. 1192.
Drukarev E.G., Ryskin M.G., Sadovnikova V.A. // Nucl. Phys. A. 2017. V. 959. P. 129.
Kaiser N., de Homont P., Weise W. // Phys. Rev. C. 2008. V. 77. Art. № 025204.
Kaiser N., Fritsch S., Weise W. // Nucl. Phys. A. 2002. V. 697. P. 255.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая