Известия РАН. Серия физическая, 2019, T. 83, № 9, стр. 1184-1188
Особенности определения коэффициентов в разложении электрической энергии кристаллов группы A2ВХ4 по поляризации на основе исследования динамики процессов переполяризации методом гармонического анализа
В. В. Горбатенко 1, *, Б. Н. Прасолов 2, С. А. Горбатенко 3
1 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Воронежский государственный технический университет”
Воронеж, Россия
2 Закрытое акционерное общество “Научно-производственная фирма “Сенсор”
Воронеж, Россия
3 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Воронежский государственный институт физической культуры”
Воронеж, Россия
* E-mail: vlgorbatenko@mail.ru
Поступила в редакцию 12.11.2018
После доработки 29.03.2019
Принята к публикации 27.05.2019
Аннотация
На основе изучения динамики процессов переполяризации в кристаллах группы A2BX4 в сегнетоэлектрической фазе в окрестности температуры фазового перехода ${{T}_{c}}$ определены величины коэффициентов разложения электрической энергии ${{W}_{c}}$ в ряд по четным степеням поляризации ${{P}_{c}}$ согласно теории Ландау–Гинзбурга–Девоншира. Произведено сравнение полученных в динамике экспериментальных результатов с теоретическими представлениями теории Ландау–Гинзбурга–Девоншира, описывающими зависимости ${{W}_{c}}({{P}_{c}})$ в статике.
ВВЕДЕНИЕ
В работах [1, 2] методом гармонического анализа [3] был исследован процесс переполяризации модельного кристалла группы A2BX4 – хлорцинката рубидия Rb2ZnCl4 под действием гармонического электрического поля с амплитудой ${{E}_{m}}$ выше напряженности коэрцитивного поля ${{E}_{k}}.$ Временная зависимость плотности тока ${{J}_{x}}(t),$ возникающая в образце под действием гармонического поля, имеет сложную периодическую форму. Зависимость ${{J}_{x}}(t)$ включает в себя две составляющие – емкостную ${{J}_{c}}(t)$ и плотность тока проводимости ${{J}_{g}}(t).$
Исследование гармоник плотности тока ${{J}_{c}}(t)$ и ${{J}_{g}}(t)$ позволило построить зависимость электрической энергии ${{W}_{c}}$ единицы объема исследуемого образца от его поляризации ${{P}_{c}}.$ Измерения проводились на инфранизких частотах, практически в статическом режиме. Результаты эксперимента достаточно хорошо согласуются с теоретическими представлениями Ландау–Гинзбурга–Девоншира [4, 5].
Согласно ЛГД-теории [4, 5], в случае одноосного сегнетоэлектрика можно разложить свободную энергию ${{W}_{c}}$ по степеням единственной компоненты поляризации ${{P}_{c}}.$ Таким образом, имеем:
(1)
${{W}_{c}} = \frac{1}{2}aP_{c}^{2} + \frac{1}{4}bP_{c}^{4} + \frac{1}{6}cP_{c}^{6} + ... - E{{P}_{c}},$Известно, что равновесная конфигурация определяется минимумом ${{W}_{c}}({{P}_{c}}).$ Это уравнение дает выражение для электрического поля Е как функции поляризации ${{P}_{c}}{\text{:}}$
Это справедливо в том случае, если
т.е. когда E = const.
Высказанные предположения хорошо подтверждаются экспериментальными исследованиями ${{W}_{c}}({{P}_{c}})$ на инфранизких частотах [1].
В настоящей работе изучение динамики процессов переполяризации в кристаллах группы A2BX4 в сегнетоэлектрической фазе в окрестности температуры фазового перехода ${{T}_{c}}$ проводилось на частотах, при которых нельзя не учитывать инерционных свойств, связанных с переключением доменной структуры. По результатам гармонического анализа петель диэлектрического гистерезиса, полученных при воздействии на образец синусоидального электрического поля, напряженность которого выше коэрцетивного, исследовалась динамическая зависимость потенциального рельефа движения сегнетоэлектрического иона под воздействием электрического поля, т.е. зависимость электрической энергии ${{W}_{c}}$ единицы объема исследуемого образца от его поляризации ${{P}_{c}}.$ Результаты эксперимента сопоставляли с теоретическими представлениями Ландау, Гинзбурга и Девоншира.
МЕТОДИКА ЭКСПЕРИМЕНТА И ОБРАЗЦЫ
В работе использован метод параллельного гармонического анализа [3] действительных и мнимых составляющих плотности тока (или поляризации) для исследования нелинейных диэлектрических свойств сегнетоэлектрических кристаллов при воздействии на образец гармонического напряжения. Схема установки, реализующей указанную методику, подробно описана в [1, 2]. Эквивалентная электрическая схема замещения исследуемого образца представляется в виде параллельного включения емкости ${{C}_{x}}$ и проводимости ${{G}_{x}}.$
Согласно данному методу, в исследуемых образцах кристаллов группы A2BX4 вследствие приложения к ним переменного электрического поля $E(t) = {{E}_{m}}\sin {{\omega }_{{\text{0}}}}t$ с частотой ${{{\omega }}_{{\text{0}}}}$ и амплитудой ${{E}_{m}},$ достаточной для полной монодоменизации образца, возникает ток сложной периодической формы. Временная зависимость плотности этого тока описывается рядом Фурье:
(4)
${{J}_{x}}(t) = \sum\limits_{k = 1}^\infty {{{J}_{k}}} \cos (k{{\omega }_{{\text{0}}}}t - \left| {{{\varphi }_{k}}} \right|),$Зависимость ${{J}_{x}}(t)$ включает в себя две составляющие, ${{J}_{c}}(t)$ и ${{J}_{g}}(t).$ Первая составляющая ${{J}_{c}}(t) = \sum\nolimits_{k = 1}^\infty {{{J}_{k}}} \cos {{\varphi }_{k}}\cos k{{\omega }_{0}}t$ обусловлена емкостной плотностью тока, а вторая составляющая ${{J}_{g}}(t) = \sum\nolimits_{k = 1}^\infty {{{J}_{k}}} \sin {{\varphi }_{k}}\sin k{{\omega }_{{\text{0}}}}t$ обусловлена плотностью тока проводимости.
Временная зависимость общей плотности тока ${{J}_{x}}(t) = {{J}_{c}}(t) + {{J}_{g}}(t)$ приводит к временной зависимости поляризации ${{P}_{x}}(t),$ возникающей в эталонном конденсаторе схемы Сойера–Тауэра. Зависимость ${{P}_{x}}(t),$ имеющая две составляющие ${{P}_{c}}(t)$ и ${{P}_{g}}(t),$ описывается выражением:
(5)
${{P}_{x}}(t) = \sum\limits_{k = 1}^\infty {{{P}_{k}}} \sin (k{{\omega }_{{\text{0}}}}t - {{\varphi }_{k}}),$Составляющая ${{P}_{c}}(t) = \sum\nolimits_{k = 1}^\infty {{{P}_{k}}} \cos {{\varphi }_{k}}\sin k{{\omega }_{{\text{0}}}}t,$ обусловленная емкостной плотностью тока ${{J}_{c}}(t),$ соответствует временной зависимости поляризации исследуемого образца. Вторая составляющая ${{P}_{g}}(t) = \sum\nolimits_{k = 1}^\infty {{{P}_{k}}} \sin {{\varphi }_{k}}\cos k{{\omega }_{{\text{0}}}}t$ обусловлена протеканием через эталонный конденсатор тока проводимости исследуемого образца, плотность которого ${{J}_{g}}(t).$
Таким образом, после измерения амплитуд гармоник ${{P}_{k}}$ и ${{J}_{k}}$ и соответствующих им углов ${{\varphi }_{k}}$ обработка результатов измерений программным путем обеспечивает синтез петель диэлектрического гистерезиса, зависимости диэлектрической проницаемости измерительного образца ${{\varepsilon }_{x}},$ его удельной проводимости ${{g}_{x}}$ и т.д. от приложенного поля $E(t).$ Возможность вводить или удалять при синтезе отдельные спектральные составляющие плотности тока и (или) поляризации, амплитуды которых ${{J}_{k}}$ и ${{P}_{k}},$ позволяет оперативно оценивать их влияние на формы получаемых зависимостей, что облегчает интерпретацию результатов измерений, полученных ранее другими способами.
Измерения проводились на образцах кристаллов группы А2ВХ4 (Rb2ZnCl4, К2ZnCl4, (NH4)2ZnCl4, (NH4)2ZnBr4) x-среза в форме прямоугольных пластин размером 7 × 5 × 0.5 мм3 с напыленными серебряными электродами.
РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТА И ОБСУЖДЕНИЕ
При изотермической выдержке исследуемых образцов кристаллов группы А2ВХ4 (Rb2ZnCl4, К2ZnCl4, (NH4)2ZnCl4, (NH4)2ZnBr4), в сегнетоэлектрической фазе в равновесных условиях [7–9] в окрестности температуры точки Кюри ${{T}_{c}}$ проводились измерения составляющих гармоник поляризации ${{P}_{k}}$ и плотности тока ${{J}_{k}}$ при амплитудах напряженности синусоидального электрического поля ${{E}_{m}},$ приложенного к исследуемому образцу, выше коэрцитивного ${{E}_{k}},$ с частотой 5 Гц.
Амплитуды гармоник ${{P}_{k}}$ и соответствующие им углы ${{\varphi }_{k}}$, измеренные при изотермической выдержке исследуемых образцов при температуре Т = Тc = –2.5 К, позволили синтезировать временные и полевые зависимости компонент поляризации и плотности тока. Временные зависимости ${{P}_{x}}(t),$ ${{P}_{c}}(t),$ ${{P}_{g}}(t),$ ${{J}_{x}}(t),$ ${{J}_{c}}(t)$ и ${{J}_{g}}(t)$ исследуемого образца кристалла Rb2ZnCl4 представлены на рис. 1. Вышеперечисленные зависимости наблюдаются при приложении к обкладкам исследуемого образца гармонического электрического поля амплитудой ${{E}_{m}}$ = 1.6 · 105 В ∙ м–1.
Рис. 1.
Зависимости компонент поляризаций и плотности токов от нормированного времени ${{{\omega }}_{0}}t{\text{:}}$ а − ${{P}_{x}}$ (кривая 1), ${{J}_{x}}$ (кривая 2); б − ${{P}_{c}}$ (кривая 1), ${{J}_{c}}$ (кривая 2); в − ${{P}_{g}}$(кривая 1), ${{J}_{g}}$(кривая 2).

Как видно из рис. 1, увеличение поляризации ${{P}_{x}}(t),$ сопровождающееся движением доменных стенок, начинается в момент времени появления первых импульсов ${{J}_{x}},$ ${{J}_{c}}$ и ${{J}_{g}}$ и заканчивается в момент их исчезновения. Наличие первого импульса ${{J}_{x}}$ говорит о том, что энергия на зарядку емкости измерительного образца ${{C}_{x}},$ т.е. на появление емкостного тока плотностью ${{J}_{c}},$ и энергия на перенос заряда вследствие движения доменных стенок, т.е. на появление тока проводимости плотностью ${{J}_{g}},$ берется из источника эдс. Вторые импульсы плотности токов ${{J}_{c}}$ и ${{J}_{g}}$ равны по величине и направлены встречно, а второй импульс ${{J}_{x}}$ отсутствует. Это говорит о том, что имеет место разрядка емкости ${{C}_{x}}$ через проводимость образца ${{G}_{x}},$ т.е. перенос заряда вследствие движения доменных стенок связан с разрядом емкости ${{C}_{x}}$ измерительного образца, ранее заряженной первым импульсом.
В работе [10] показано, что в момент нормированного времени ${{\omega }_{0}}t = n\pi ,$ где n = 0, 1, 2, …, внешнее электрическое поле $E(t) = {{E}_{m}}\sin {{\omega }_{0}}t$ равно нулю, т.е. практически в момент короткого замыкания исследуемого образца его поляризация ${{P}_{c}}$ равна нулю. Для сегнетоэлектриков в отсутствие внешнего электрического поля поляризация ${{P}_{c}}$ может быть равна нулю только в том случае, если половина объема исследуемого образца (назовем ее “положительным доменом”) имеет поляризацию ${{P}_{s}},$ а другая половина (“отрицательный домен”) имеет поляризацию $ - {{P}_{s}}.$
В этом случае временные зависимости поляризации “положительного домена” (${{P}_{{cp}}}$) и “отрицательного домена” (${{P}_{{cn}}}$) будут описываться следующими выражениями:
Внешнее электрическое поле можно представить состоящим из двух составляющих
которые связаны с поляризацией положительного и отрицательного домена соответственно, т.е.
(10)
$\begin{gathered} E(t) = \frac{{{{E}_{m}}}}{{2\cos \varphi }}\sin ({{\omega }_{0}}t - {{\varphi }_{1}}) + \\ + \,\,\frac{{{{E}_{m}}}}{{2\cos \varphi }}\sin ({{\omega }_{0}}t + {{\varphi }_{1}}) = {{E}_{m}}\sin {{\omega }_{0}}t. \\ \end{gathered} $Графики зависимостей ${{P}_{{cp}}}\left( t \right)$ и ${{E}_{1}}(t)$ изображены на рис. 2а (кривая 1 и 2 соответственно), а графики зависимостей ${{P}_{{cn}}}(t)$ и ${{E}_{2}}(t)$ – на рис. 2б (кривая 1 и 2 соответственно). Тогда электрическая энергия ${{W}_{{\text{o}}}}(t),$ забираемая из источника внешнего электрического поля $E(t) = {{E}_{m}}\sin {{\omega }_{0}}t,$ состоит из энергии положительного домена
(11)
$\begin{gathered} {{W}_{{cp}}}(t) = {{P}_{{cp}}}(t){{E}_{1}}(t) = \\ = \left[ {{{P}_{c}}(t) + {{P}_{g}}(t)} \right]\frac{{{{E}_{m}}}}{{2\cos \varphi }}\sin ({{\omega }_{0}}t - {{\varphi }_{1}}). \\ \end{gathered} $Рис. 2.
Зависимости поляризации и напряженности электрического поля “положительного” и “отрицательного” доменов от нормированного времени ${{{\omega }}_{0}}t{\text{:}}$ а − ${{P}_{{cp}}}$ (кривая 1), ${{E}_{1}}$ (кривая 2); б − ${{P}_{{cn}}}$ (кривая 1), ${{E}_{2}}$ (кривая 2).

и энергии отрицательного домена
(12)
$\begin{gathered} {{W}_{{cn}}}(t) = {{P}_{{cn}}}(t){{E}_{2}}(t) = \\ = \left[ {{{P}_{c}}(t) - {{P}_{g}}(t)} \right]\frac{{{{E}_{m}}}}{{2\cos \varphi }}\sin ({{\omega }_{0}}t + {{\varphi }_{1}}). \\ \end{gathered} $Таким образом,
(13)
${{W}_{{\text{o}}}}(t) = {{P}_{c}}(t){{E}_{m}}\sin {{\omega }_{0}}t - {{P}_{g}}(t){\text{tg}}({{\varphi }_{1}}){{E}_{m}}\cos {{\omega }_{0}}t.$Энергия ${{W}_{E}}{\text{(}}t{\text{),}}$ затрачиваемая на создание гармонического поля $E(t) = {{E}_{m}}\sin {{\omega }_{0}}t,$ приложенного к исследуемому образцу, определяется выражением:
(14)
$\begin{gathered} {{W}_{E}}{\text{(}}t{\text{)}} = \int\limits_0^t {{{P}_{c}}{\text{(}}t{\text{)}}{{\omega }_{0}}{{E}_{m}}{\text{cos(}}{{{\omega }}_{0}}t{\text{)}}dt} + \\ + \,\,\int\limits_0^t {{{P}_{g}}{\text{(}}t{\text{)tg(}}{{\varphi }_{1}}{\text{)}}{{\omega }_{0}}{{E}_{m}}{\text{sin(}}{{\omega }_{0}}t{\text{)}}dt} = \\ = \frac{{{{E}_{m}}{{P}_{1}}}}{4}\left( {{\text{cos(}}{{{\varphi }}_{{\text{1}}}}{\text{)}} + {\text{tg(}}{{{\varphi }}_{{\text{1}}}}{\text{)sin(}}{{{\varphi }}_{{\text{1}}}}{\text{)}}} \right) \times \\ \times \,\,\left[ {1 - {\text{cos}}\left( {2{{\omega }_{0}}t} \right)} \right] + \tfrac{{{{E}_{m}}}}{2} \times \\ \times \,\,\sum\limits_{k = 3}^\infty {\left[ {\frac{{{{P}_{k}}}}{{{\text{(}}k - 1{\text{)}}}}} \right.} {\text{(cos(}}{{\varphi }_{k}}{\text{)}} - {\text{tg(}}{{\varphi }_{1}}{\text{)sin(}}{{\varphi }_{k}}{\text{))}} \times \\ \times \,\,\left[ {1 - {\text{cos((}}k - 1{\text{)}}{{\omega }_{0}}t} \right] + \frac{{{{P}_{k}}}}{{{\text{(}}k + 1{\text{)}}}}{\text{(cos(}}{{\varphi }_{k}}{\text{)}} + \\ + \,\,\left. {_{{_{{_{{_{{_{{}}}}}}}}}}^{{^{{^{{^{{^{{}}}}}}}}}}{\text{tg(}}{{\varphi }_{1}}{\text{)sin(}}{{\varphi }_{k}}{\text{))}}\left[ {1 - {\text{cos((}}k + 1{\text{)}}{{\omega }_{0}}t} \right]} \right]. \\ \end{gathered} $Таким образом, электрическая энергия ${{W}_{c}}(t)$ исследуемого образца
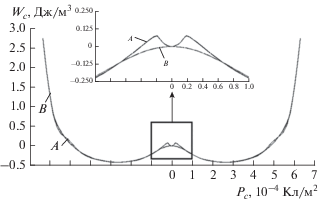
Синтезированная зависимость ${{W}_{c}}({{P}_{c}})$ показана на рис. 3 (кривая А). Используя координаты последовательно 10, 11, 12 и 13 точек зависимости ${{W}_{c}}({{P}_{c}}),$ были определены величины коэффициентов выражения (1).
Рис. 3.
Зависимости электрической энергии ${{W}_{c}}$ единицы объема исследуемого образца от его поляризации ${{P}_{c}},$ построенные с использованием метода гармонического анализа (кривая А) и разложения в ряд по поляризации, ограничиваясь членами до двадцать шестой степени (кривая B).
Зависимость величин коэффициентов a, b и c от количества N координат точек приведена в табл. 1.
Таблица 1.
Зависимость величин коэффициентов a, b и c от количества N координат точек
| N | a | b | c |
|---|---|---|---|
| 10 | –1.268 ⋅ 108 | 2.016 ⋅ 1016 | –1.127 ⋅ 1024 |
| 11 | –1.274 ⋅ 108 | 2.059 ⋅ 1016 | –1.290 ⋅ 1024 |
| 12 | –1.288 ⋅ 108 | 2.154 ⋅ 1016 | –1.32 ⋅ 1024 |
| 13 | –1.291 ⋅ 108 | 2.175 ⋅ 1016 | –1.35 ⋅ 1024 |
Зависимость ${{W}_{c}}({{P}_{c}})$, построенная согласно выражению (1) с использованием 13 членов разложения, показана на рис. 3 (кривая В).
Кривые А и В практически полностью совпадают, исключая область малых значений величин электрического поля $E(t).$ По всей видимости, для более полного совпадения кривых А и В в области малых значений величин поля $E(t)$ необходимо использовать большее количество членов разложения выражения (1). Качественно аналогичные результаты были получены и на других исследуемых образцах группы А2ВХ4 (К2ZnCl4, (NH4)2ZnCl4, (NH4)2ZnBr4).
В теории Ланда–Гинзбурга–Девоншира считается, что в окрестности точки Кюри ${{T}_{C}}$ коэффициент $a$ изменяется с температурой:
Предполагается, что ${{a}_{0}}$ и c положительны для всех известных сегнетоэлектриков [11, 12], а род фазового перехода определяется коэффициентом b.
Согласно результатам экспериментов настоящей работы, коэффициент c отрицателен для всех исследуемых образцов. Этот факт может быть следствием одновременного проявления регистрации особенностей свойств переходов первого и второго рода (малый скачок поляризации и увеличение ее с уменьшением температуры). Возможно данный факт связан с особенностями измерения коэффициентов a, b и c в динамическом режиме.
Учитывая динамические особенности измерения поляризации, имеем
где(18)
${{E}_{{{\text{св}}}}}(t) = {\text{tg}}({{\varphi }_{1}}){{E}_{m}}\cos {{\omega }_{0}}t\frac{{{{J}_{g}}(t)}}{{{{J}_{c}}(t)}}.$Результаты экспериментов для всех исследуемых образцов кристаллов группы А2ВХ4 (Rb2ZnCl4, К2ZnCl4, (NH4)2ZnCl4, (NH4)2ZnBr4) подтверждают, что
(19)
$a{{P}_{c}}(t) + P_{c}^{3}(t) + P_{c}^{5}(t) + ... - {{E}_{{{\text{св}}}}}(t) = {{E}_{m}}\sin {{\omega }_{0}}t.$На основании результатов экспериментов исследуемых образцов кристаллов группы А2ВХ4 можно сделать следующие выводы:
1) увеличение чувствительности измерительной аппаратуры и числа регистрируемых гармоник по сравнению с возможностями предыдущей установки позволило обнаружить локальный минимум зависимостей ${{W}_{c}}({{P}_{c}})$ в момент ${{P}_{c}} = 0;$
2) зависимости ${{W}_{c}}({{P}_{c}}),$ построенные методом гармонического анализа и восстановленные согласно выражению (1), практически совпадают, если учитывать не менее 13 коэффициентов в разложении ${{W}_{c}}$ по четным степеням ${{P}_{c}};$
3) обнаружен разный знак при коэффициенте с в выражении (1), полученном экспериментально и предполагаемом из ЛГД-теории;
4) при аппроксимации зависимости $E({{P}_{c}})$ нужно учитывать инерционные свойства исследуемого образца.
Список литературы
Горбатенко В.В., Кудряш В.И., Прасолов Б.Н. и др. // Изв. РАН. Сер. физ. 2011. Т. 75. № 10. С. 1394; Gorbatenko V.V., Kudryash V.I., Prasolov B.N. et al. // Bull. Russ. Acad. Sci. Phys. 2011. V. 75. № 10. Р. 1313.
Горбатенко В.В., Прасолов Б.Н., Кудряш В.И. и др. // Изв. РАН. Сер. физ. 2010. Т. 74. № 9. С. 1294; Gorbatenko V.V., Kudryash V.I., Prasolov B.N. et al. // Bull. Russ. Acad. Sci. Phys. 2010. V. 74. № 9. P. 1240.
Харкевич А.А. Спектры и анализ. М.: ГИФМЛ, 1962. 236 с.
Ландау Л.Д., Лившиц Е.М. Статистическая физика. М.: Наука, 1976. 486 с.
Devonshire A.F. // Adv. Phys. 1954. V. 3. P. 85.
Рабе К.М., Ана Ч.Г., Трискона Ж.-М. Физика сегнетоэлектриков (современный взгляд). М.: БИНОМ. Лаборатория знаний, 2011. С. 89.
Гриднев С.А., Горбатенко В.В., Прасолов Б.Н. // Кристаллография. 1994. Т. 39. С. 106.
Гриднев С.А., Прасолов Б.Н., Горбатенко В.В. // ФТТ. 1990. Т. 32. № 7. С. 2171.
Prasolov B.N., Gorbatenko V.V., Safonova I.A. // Ferroelectrics. 1996. V. 186. P. 231.
Горбатенко В.В., Прасолов Б.Н., Горбатенко С.А. // Изв. РАН. Сер. физ. 2018. Т. 82. № 3. С. 280; Gorbatenko V.V., Prasolov B.N., Gorbatenko S.A. // Bull. Russ. Acad. Sci. Phys. 2018. V. 82. № 3. P. 280.
Fatuzzo E., Mertz W.M. Ferroelectricity. Amsterdam, 1967. 289 p.
Лайнс М., Гласс А. Сегнетоэлектрики и родственные им материалы. М.: Мир, 1981. 736 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая


