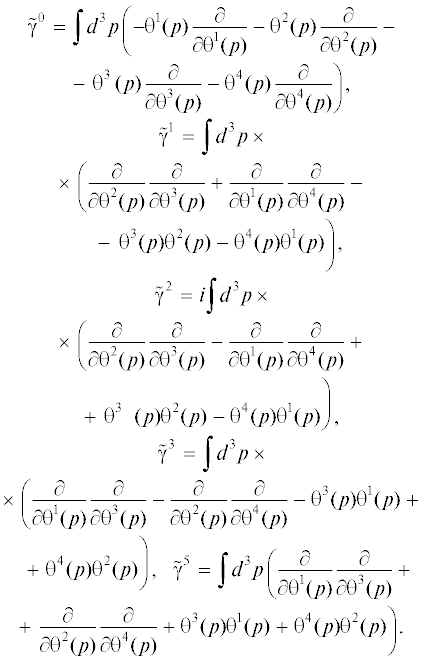Известия РАН. Серия физическая, 2019, T. 83, № 9, стр. 1282-1287

ВВЕДЕНИЕ

Уравнение Дирака [1], предложенное в 1928 году, является основой теорий с участием фермионов. В квантово-полевом рассмотрении его решения приходится трактовать в формализме вторичного квантования, который для систем фермионов был предложен в 1928 году Вигнером и Иорданом [2] и доработан в 1934 году Гейзенбергом [3]. Современная формулировка метода, основанная на супералгебраическом подходе, и его математический аппарат даны в работах Березина [4, 5].

В методе вторичного квантования решение уравнения Дирака при использовании гамма-матриц в представлении Дирака записывается в виде [6, 7]:

где $t = {{x}^{0}},$ $x$ означает ${{x}^{1}},{{x}^{2}},{{x}^{3}},$ $\alpha = 1,2;$ $\tau = 3,4,$ $E = {{p}_{0}}$ и считается ${{p}_{0}} > 0,$ а по повторяющимся индексам подразумевается суммирование.

В (1) $\Psi (t,x)$ – оператор поля фермиона в точке $x$ пространства-времени, $a_{1}^{ + }(p)$ – оператор рождения фермиона с 4-импульсом $p$ и спином вверх, ${{a}_{1}}(p)$ – оператор уничтожения такого фермиона, $a_{3}^{ + }(p)$ – оператор рождения антифермиона с 4-импульсом $p$ и спином вверх, ${{a}_{3}}(p)$ – оператор уничтожения такого антифермиона. Для индексов 2 и 4 – то же для состояний со спином вниз [7].

Эрмитово-сопряженное решение [7] записывается в виде:

В (1) и (2) ${{u}^{\alpha }}(p)$ – базисные спиноры, соответствующие положительно-частотным решениям с заданным импульсом ${{p}_{\mu }},$ ${{v}^{\tau }}(p)$ – базисные спиноры, соответствующие отрицательно-частотным решениям, $\,{{\bar {u}}^{\alpha }} = {{({{u}^{\alpha }})}^{ + }}{{\gamma }^{0}}$ и ${{\bar {v}}^{\tau }} = {{({{v}^{\tau }})}^{ + }}{{\gamma }^{0}}$ – соответствующие им сопряженные спиноры.

Вторичное квантование, то есть разложения (1) и (2), получается заменой числовых коэффициентов $\,{{b}_{\alpha }}(p)\,,\,{{b}_{\alpha }}^{ + }(p),\,{{d}_{\tau }}(p),{{d}_{\tau }}{{(p)}^{ + }}$ в решении уравнения Дирака на операторнозначные [7].

1. СУПЕРАЛГЕБРАИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СПИНОРОВ, МАТРИЦ ДИРАКА И УРАВНЕНИЯ ДИРАКА

В работах [8, 9] автором предложено супералгебраическое представление спиноров и матриц Дирака. В нем спиноры являются алгебраическими объектами, представляющими собой суперпозицию грассмановых переменных, а матрицы Дирака выражаются через эти грассмановы переменные и производные по ним. Линейные преобразования грассмановых переменных порождают преобразования Лоренца [4]. Недостаток данного подхода в том, что он не согласовался с разложением (2) вторичного квантования. В работе [10] автор построил супералгебраическое представление спиноров, лишенное данного недостатка. Оно является фермионным аналогом представления Баргмана–Фока для бозонов и основано на использовании грассмановых переменных, являющихся плотностями в пространстве импульсов, и производных по этим переменным. Супералгебраическим аналогом гамма-матриц Дирака являются коммутаторы

где * означает, что на это место следует поставить величину, стоящую справа, на которую действует данный оператор, а величины ${{\tilde {\gamma }}^{\eta }}$ заданы как

Наличие коммутатора в определении гамма-матриц в (3) и других операторов, действующих на спиноры, приводит к тому, что в теории не появляются бесконечные постоянные суммы, и поэтому теория не требует нормализации операторов [10].

Оператор

где u_α(p) и v_τ(p) числовые множители, переводится в эрмитово-сопряженный [10] по правилу (6):

Преобразования Лоренца строятся обычным образом с помощью гамма-матриц (3) и могут рассматриваться как преобразования Боголюбова операторов рождения–уничтожения.

Для оператора $\Psi $ спинора в супералгебраическом представлении уравнение Дирака приобретает вид

Введем дираковски-сопряженный оператор

Сделаем эрмитово сопряжение (7) и домножим на $ - {{\hat {\gamma }}^{0}}.$ С учетом (8) и того, что ${{\hat {\gamma }}^{0}}{{({{\hat {\gamma }}^{\mu }})}^{ + }} = {{\hat {\gamma }}^{\mu }}{{\hat {\gamma }}^{0}},$ получим (9):

Решения уравнений (7) и (9) могут быть записаны в виде

В формулах (10), (11) $\,{{\lambda }_{\alpha }}$ и ${{\lambda }_{\tau }}$ – константы (возможно, зависящие от $p$), операторы ${{b}_{\alpha }}(p)$ и ${{d}_{\tau }}(p)$ получены лоренцевыми вращениями величин $\frac{\partial }{{\partial {{\theta }^{\alpha }}(0)}}$ и $\frac{\partial }{{\partial {{\theta }^{\tau }}(0)}},$ а операторы ${{\bar {b}}_{\alpha }}(p)$ и ${{\bar {d}}_{\tau }}(p)$ получены лоренцевыми вращениями из величин ${{\theta }^{\alpha }}(0)$ и ${{\theta }^{\tau }}(0).$

Величины ${{b}_{\alpha }}(p),$ ${{d}_{\tau }}(p)$ и их дираковски-сопряженные ${{\bar {b}}_{\alpha }}(p)$ и ${{\bar {d}}_{\tau }}(p)$ обладают антикоммутационными соотношениями (12) операторов рождения и уничтожения

Пусть у нас имеются величина $\Psi (p)$ из (6) и $\Phi (p),$ задаваемая выражением (13)

Скалярное произведение Ψ(p') и Φ(p) в супералгебраическом представлении задается антикоммутатором (14):

Очевидно выполнение всех свойств скалярного произведения.

2. СВЯЗЬ ОПЕРАТОРОВ РОЖДЕНИЯ И УНИЧТОЖЕНИЯ С ГРАССМАНОВЫМИ ПЛОТНОСТЯМИ

Рассмотрим преобразование решений уравнения Дирака в супералгебраической форме более подробно на примере буста на угол $\phi $ в плоскости ${{\hat {\gamma }}^{0}}{{\hat {\gamma }}^{1}}.$ Пусть в состоянии покоя, то есть для $p = 0,$ имеются базисные спиноры

Тогда после буста на угол $\phi $ в плоскости ${{\hat {\gamma }}^{0}}{{\hat {\gamma }}^{1}}$

При этом множитель ${{e}^{{ - i{{p}_{0}}{{x}^{0}}}}}$ переходит в ${{e}^{{ - i{{p}_{\mu }}{{x}^{\mu }}}}},$ а ${{e}^{{i{{p}_{0}}{{x}^{0}}}}}$ в ${{e}^{{i{{p}_{\mu }}{{x}^{\mu }}}}}.$

Уравнения (16) можно переписать в виде

при этом

Сравнивая (10) с (1) с учетом (17), (18) и законом преобразования входящих в (1) спиноров ${{u}^{\alpha }}$ и ${{v}^{\tau }}$ [7], получаем, что компоненты ${{u}^{\alpha }}$ и ${{v}^{\tau }}$ в (17) преобразуются таким же образом. Если считать, согласно [10], что выполняется соответствие (19)

то (10) можно переписать в виде

где ${{a}_{k}}(p) = \frac{\partial }{{\partial {{\theta }^{k}}(p)}},$ ${{a}_{k}}{{(p)}^{ + }} = {{\theta }^{k}}(p).$ Таким образом, в (20) мы получаем полный аналог обычной формулы вторичного квантования для фермионов. В ней роль операторов рождения выполняют грассмановы плотности ${{\theta }^{k}}(p),$ а роль операторов уничтожения – производные $\frac{\partial }{{\partial {{\theta }^{k}}(p)}}$ по этим плотностям. При этом обычная схема является упрощенным вариантом супералгебраической, так как в ней отсутствует зависимость образующих (матричных столбцов и строк) от импульса.

3. БИЛИНЕЙНЫЕ КОВАРИАНТЫ

Рассмотрим для произвольных спиноров $\Psi $ и $\Phi $ пассивные преобразования Лоренца билинейных ковариантов $\left( {{{{\hat {\gamma }}}^{0}}\Psi _{1}^{'},\Psi _{2}^{'}} \right),\,\,\,\,\left( {{{{\hat {\gamma }}}^{0}}\Psi _{1}^{'},{{{\hat {\gamma }}}^{{\mu '}}}\Psi _{2}^{'}} \right),$ $\left( {{{{\hat {\gamma }}}^{0}}\Psi _{1}^{'},{{{\hat {\gamma }}}^{{\mu '}}}{{{\hat {\gamma }}}^{{\nu '}}}\Psi _{2}^{'}} \right),$ и т.д. В них используется скалярное произведение супералгебраических спиноров (14). Штрихами, как и ранее, отмечены величины, которые относятся к движущейся системе отсчета, а ${{\hat {\gamma }}^{0}}$ относится к собственной системе покоя спинора. Поскольку преобразование Лоренца, связанное с переходом к движущейся системе отсчета, это пассивное преобразование, оно не меняет алгебраические ковариантные величины. Поэтому

где $\Psi $ – произвольный спинор, ${{a}_{\mu }}$ – ковариантные компоненты произвольного вектора, ${{a}_{{\mu \nu }}}$ – ковариантные компоненты произвольного тензора второго ранга, и т.д.

Из (21) сразу следует, что $\left\{ {\bar {\Psi }_{1}^{'},\Psi _{2}^{'}} \right\} = \{ {{\bar {\Psi }}_{1}},{{\Psi }_{2}}\} .$ То есть $\left( {{{{\hat {\gamma }}}^{0}}\Psi _{1}^{'},\Psi _{2}^{'}} \right) = ({{\hat {\gamma }}^{0}}{{\Psi }_{1}},{{\Psi }_{2}}),$ и величина $({{\hat {\gamma }}^{0}}{{\Psi }_{1}},{{\Psi }_{2}})$ = = $\{ {{\bar {\Psi }}_{1}},{{\Psi }_{2}}\} $ является скаляром.

Для выяснения закона преобразования других билинейных ковариантов сначала рассмотрим закон преобразования гамма-матриц. Контравариантные компоненты ${{a}^{\mu }}$ произвольного вектора $a$ при пассивном преобразовании Лоренца преобразуются как ${{a}^{{'\mu }}} = \Lambda _{\nu }^{\mu }{{a}^{\nu }},$ а ковариантные как $a_{\mu }^{'} = ({{\Lambda }^{{ - 1}}})_{\mu }^{\nu }{{a}_{\nu }}.$ Поскольку при таком преобразовании ${{\hat {\gamma }}^{{\mu '}}}a_{\mu }^{'} = {{\hat {\gamma }}^{\mu }}{{a}_{\mu }},$ получаем ${{\hat {\gamma }}^{{\nu '}}}({{\Lambda }^{{ - 1}}})_{\nu }^{\mu }{{a}_{\mu }} = {{\hat {\gamma }}^{\mu }}{{a}_{\mu }}.$ В силу произвольности ${{a}_{\mu }}$ получаем ${{\hat {\gamma }}^{\mu }} = ({{\Lambda }^{{ - 1}}})_{\nu }^{\mu }{{\hat {\gamma }}^{{\nu '}}}.$ Отсюда ${{\hat {\gamma }}^{{\mu '}}} = \Lambda _{\nu }^{\mu }{{\hat {\gamma }}^{\nu }}.$ То есть ${{\hat {\gamma }}^{\mu }}$ преобразуется как контравариантная величина, что совпадает с обычной формулой теории Дирака. Поэтому ${{\hat {\gamma }}^{{{{\mu }_{1}}'}}}{{\hat {\gamma }}^{{{{\mu }_{2}}'}}}...{{\hat {\gamma }}^{{{{\mu }_{k}}'}}} = \Lambda _{{{{\nu }_{1}}}}^{{{{\mu }_{1}}}}{{\hat {\gamma }}^{{{{\nu }_{1}}}}}\Lambda _{{{{\nu }_{2}}}}^{{{{\mu }_{2}}}}{{\hat {\gamma }}^{{{{\nu }_{2}}}}}...\Lambda _{{{{\nu }_{k}}}}^{{{{\mu }_{k}}}}{{\hat {\gamma }}^{{{{\nu }_{k}}}}}.$ Отсюда сразу получаем

Формула (22) совпадает с обычной формулой для билинейных ковариантов [6, 7]. Необходимо отметить, что если бы в скалярное произведение (14) входила величина $\Psi ',$ а не ${{\hat {\gamma }}^{0}}\Psi ',$ в антикоммутаторе вместо лоренц-ковариантной величины $\bar {\Psi }'$ присутствовала бы нековариантная величина ${{\Psi }^{ + }}',$ и проведенные рассуждения были бы некорректны.

4. ПЛОТНОСТЬ ЛАГРАНЖИАНА И НЁТЕРОВСКИЕ ТОКИ

Совершенно аналогично тому, как это сделано в [7] в матричном формализме, но только с использованием скалярного произведения спиноров (14), исходя из супералгебраического уравнения Дирака при отсутствии электромагнитного поля (7), можно построить плотность лагранжиана.

Величины $\Psi (x)$ раскладываются по спинорному базису $\frac{\partial }{{\partial {{\theta }^{1}}(p)}},$ $\frac{\partial }{{\partial {{\theta }^{2}}(p)}},$ ${{\theta }^{3}}(p),\,\,{{\theta }^{4}}(p)$ (по всем значениям $p$), а величины $\bar {\Psi }(x)$ раскладываются по линейно независимому от него спинорному базису ${{\theta }^{1}}(p),\,\,{{\theta }^{2}}(p),$ $\frac{\partial }{{\partial {{\theta }^{3}}(p)}},$ $\frac{\partial }{{\partial {{\theta }^{4}}(p)}}$ (по всем значениям $p$). Поэтому они являются линейно независимыми, и их вариации $\delta \Psi (x)$ и $\delta \bar {\Psi }(x)$ можно рассматривать как независимые. Для построения вариации $\delta S$ действия $S$ при изменении величины $\bar {\Psi }(x)$ без изменения $\Psi (x)$ возьмем антикоммутатор уравнения Дирака с вариацией $\delta \bar {\Psi }(x)$ и проинтегрируем по всему объему $V$пространства, а также по времени от момента ${{t}_{1}}$ до момента ${{t}_{2}}{\text{:}}$

Таким образом,

Или, что то же,

По виду выражение (24) совпадает с аналогичным выражением $L(x)$ в матричном формализме [7] при его записи через скалярное произведение.

Покажем, что из (23) следует супералгебраическое уравнение Дирака. Из стационарности действия

следует

Из (25) благодаря независимости и произвольности вариаций получаем

Из (27) благодаря произвольности $\delta \bar {\Psi }(x)$ следует $\{ \delta \bar {\Psi }(x),$ $(i{{\hat {\gamma }}^{\mu }}{{\partial }_{\mu }} - m)\Psi (x)\} = 0,$ и в силу произвольности вариации $\delta \bar {\Psi }(x)$ и свойств скалярного произведения получаем

то есть уравнение Дирака (7). Это естественно, так как мы вводили плотность лагранжиана так, чтобы из его вариации получить данное уравнение. А вот уравнение (9) получается без такого намеренного выбора. Из (27) следует

поэтому, перенося с эрмитовым сопряжением оператор $(i{{\hat {\gamma }}^{\mu }}{{\partial }_{\mu }} - m)$ в левую часть скалярного произведения, получаем

При выводе этой формулы мы учли, что вариация $\delta \Psi (x)$ обнуляется в точках ${{t}_{1}}$ и ${{t}_{2}},$ и что значения $\Psi (x)$ на бесконечно удаленной границе пространства равны нулю, из-за чего производные ${{\partial }_{\mu }}$ при интегрировании по частям меняют знак.

Меняя местами $i{{\hat {\gamma }}^{{\mu + }}}{{\partial }_{\mu }} - m$ с ${{\hat {\gamma }}^{0}},$ получаем

В силу произвольности вариации $\delta \Psi (x)$ из этого следует

откуда опять получаем уравнение Дирака (7):

Таким образом, уравнения, получаемые на основе плотности лагранжиана (23), (24), совместны и являются одним и тем же супералгебраическим уравнением Дирака для спинора. Уравнение Дирака для антиспинора получается с помощью дираковского сопряжения уравнения Дирака для спинора – они эквивалентны.

К плотности лагранжиана можно добавить величину, являющуюся четырехмерной дивергенцией, так как она не меняет динамические уравнения. Если к плотности лагранжиана (23) прибавить добавку

являющуюся четырехмерной дивергенцией, можно получить плотность лагранжиана

из которой при вариации по $\Psi (x)$ сразу следует уравнение Дирака для антиспинора. Если же добавка равна ${{L}_{3}}(x) = L(x) + \frac{1}{2}\Delta L(x),$ мы получим еще одну эквивалентную плотность лагранжиана, в которую $\bar {\Psi }(x)$ и $\Psi (x)$ входят симметричным образом:

Плотность лагранжиана (30) является аналогом соответствующей матричной [7]

Однако в супералгебраическом варианте (34), в отличие от (31), алгебраическая симметрия $\bar {\Psi }(x)$ и $\Psi (x)$ видна явным образом.

5. НЁТЕРОВСКИЕ ТОКИ И ОПЕРАТОР СОХРАНЯЮЩЕГОСЯ ЗАРЯДА

Разделим обе части супералгебраической формы уравнения Дирака (7) на $i{\text{:}}$

Возьмем эрмитово сопряжение от (32) и умножим обе части на $ - {{\hat {\gamma }}^{0}}{\text{:}}$

В соответствии с (3), ${{({{\hat {\gamma }}^{0}}\Phi )}^{ + }} = - {{\hat {\gamma }}^{0}}{{\Phi }^{ + }}$ для произвольного $\Phi ,$ поэтому из (37) следует

Возьмем антикоммутатор обеих частей (32) с $\bar {\Psi }$ и обеих частей (34) с $\Psi {\text{:}}$

Сложим уравнения (35). Учтем, что $\{ \bar {\Psi },{{\hat {\gamma }}^{\mu }}{{\partial }_{\mu }}\Psi \} $ = = $({{\hat {\gamma }}^{0}}\Psi ,{{\hat {\gamma }}^{\mu }}{{\partial }_{\mu }}\Psi )$ и $\{ {{({{\hat {\gamma }}^{0}}{{\hat {\gamma }}^{\mu }}{{\partial }_{\mu }}\Psi )}^{ + }},\Psi \} = ({{\hat {\gamma }}^{0}}{{\hat {\gamma }}^{\mu }}{{\partial }_{\mu }}\Psi ,\Psi )$ = $({{\hat {\gamma }}^{{\mu + }}}{{\hat {\gamma }}^{0}}{{\partial }_{\mu }}\Psi ,\Psi ) = ({{\hat {\gamma }}^{0}}{{\partial }_{\mu }}\Psi ,{{\hat {\gamma }}^{\mu }}\Psi ),$ в результате чего получим $({{\hat {\gamma }}^{0}}\Psi ,{{\hat {\gamma }}^{\mu }}{{\partial }_{\mu }}\Psi )$ + $({{\hat {\gamma }}^{0}}{{\partial }_{\mu }}\Psi ,{{\hat {\gamma }}^{\mu }}\Psi ) = 0,$ т.е.

Получаем, что в (36) фигурирует ток j^μ = = $({{\hat {\gamma }}^{0}}\Psi ,{{\hat {\gamma }}^{\mu }}\Psi ),$ четырехмерная дивергенция которого равна нулю, т.е. ток сохраняющегося “заряда”:

Последний является током плотности вероятности [7], а сам “заряд” $\int_V {{{d}^{3}}x} {{j}^{0}}$ = $\int_V {{{d}^{3}}x\{ {{\Psi }^{ + }},\Psi \} } = 1$ – это единичная вероятность найти частицу во всем пространстве.

Ток ${{j}^{\mu }}$ известен как нётеровский и связан с инвариантностью лагранжиана к преобразованию $\Psi (x) \to {{e}^{{i\alpha }}}\Psi (x)$ [6]. Однако ${{e}^{{i\alpha }}}$ не может служить оператором, так как $\bar {\Psi }$ преобразуется путем умножения на другую величину, на ${{e}^{{ - i\alpha }}}.$ Введем оператор заряда

Видна единая супералгебраическая природа заряда, задаваемого выражением (38), и матриц Дирака, задаваемых выражением (4). Выражение (38) аналогично формуле для заряда, выраженного через операторы рождения–уничтожения [6, 7], в обычном методе вторичного квантования, но не содержит расходимостей и не нуждается в нормализации.

Легко проверяется, что $\hat {Q}\Psi = q\Psi $ и $\hat {Q}\bar {\Psi } = - q\bar {\Psi },$ где $q = 1,$ и что на векторах состояния он инвариантен при лоренцевских вращениях. Лагранжиан инвариантен к преобразованию $\Psi (x) \to {{e}^{{i\alpha \hat {Q}}}}\Psi (x)$ и соответствующему ему преобразованию $\bar {\Psi }(x) \to $ $ \to {{e}^{{i\alpha \hat {Q}}}}\bar {\Psi }(x),$ и мы получим ток сохраняющегося заряда, который можно трактовать как “электрический”. Если параметр преобразования $\alpha $ зависит от $x,$ обычным образом [11] вводится поле ${{A}_{\mu }}(x)$, и уравнение Дирака преобразуется к виду:

или, при записи через собственные числа оператора $\hat {Q},$

Из (40) видно, что спинор и дираковски-сопряженный к нему имеют противоположный заряд, который можно трактовать как электрический.

ЗАКЛЮЧЕНИЕ

Таким образом, построена теория спиноров, которая сразу является вторично квантованной и не требует нормализации операторов. Она расширяет теорию Дирака, обеспечивая существование операторов спиноров и дираковски-сопряженных спиноров в одном пространстве, что естественно в формализме вторичного квантования. Показано наличие оператора заряда, который имеет ту же супералгебраическую природу, что и матрицы Дирака.