Известия РАН. Серия физическая, 2020, T. 84, № 1, стр. 137-141

ВВЕДЕНИЕ

Квантовые поляризационные характеристики света играют важную роль в задачах квантовой оптики и квантовой информатики. Обычно для изучения поляризационных характеристик света применяются наблюдаемые операторы Стокса, Джонса и их дисперсии. Перечислим некоторые достижения теории и эксперимента поляризационной квантовой оптики, которые связаны с многомодовыми состояниями света.

В работе [1] была предложена и теоретически обоснована концепция поляризационно-сжатого света. Она была применена для нелинейных анизотропных сред с кубической нелинейностью. В этом же году была разработана теория и экспериментально обнаружен свет со скрытой поляризацией в нелинейной среде с квадратичной нелинейностью в монодоменном кристалле [2] при вырожденном спонтанном параметрическом рассеянии, при котором все средние значения операторов Стокса равны нулю (или значение степени поляризации равно нулю), а значение дисперсии одного из операторов Стокса отличается от других. Отметим, что среднее значение параметров Стокса при вырожденном параметрическом рассеянии равно нулю за счет неопределенности фазы между модами разных поляризаций, а скрытая поляризация появляется за счет запутанности и строгой корреляции состояний поляризации мод рождающихся бифотонов.

Следует отметить также метод поляризационной томографии квантовых состояний света с помощью функции поляризационной квазивероятности [3]. Функция поляризационной квазивероятности использовалась для различных примеров поляризационных состояний. Первый эксперимент по восстановлению функции поляризационной квазивероятности был осуществлен для спонтанного параметрического рассеяния в нелинейном монодоменном кристалле с квадратичной нелинейностью [3]. Такие состояния света полезны, например, в сверхчувствительных оптических измерениях [4] и протоколах квантовой криптографии, в частности, BB84 и E91.

В последние годы активно рассматривается применение поляризационных свойств света в обработке фантомных изображений с помощью поляризационно-запутанных состояний. В работе [5] предлагается фиксировать не просто парные совпадения фотоотсчетов, но и совпадения их состояний поляризации. При этом достигается дополнительное подавление шума.

Поляризационные характеристики света играют важную роль при изучении свойств объектов, подсвечиваемых обыкновенным или поляризованным светом, то есть в задачах поляриметрии [6], в том числе и методами формирования поляризационных фантомных изображений [7].

Обычно для приготовления квантовых поляризационных состояний света используются монодоменные нелинейные оптические кристаллы с квадратичной нелинейностью. Но в последнее время растет интерес и к кристаллам с регулярной доменной структурой (РДС). Он связан с тем, что появляется дополнительная степень свободы для реализации того или иного фазового синхронизма. В результате одновременно могут происходить различные нелинейные процессы в одном и том же кристалле, например, параметрическое рассеяние света и генерация суммарных гармоник как независимо, так и каскадно, см., например, [8].

В данной работе рассмотрены особенности квантовых статистических характеристик поляризационных состояний света для РДС-кристалла при выполнении условия квазисинхронизма двух процессов: параметрического и генерации суммарных частот методом диагонализации гамильтониана.

НЕЛИНЕЙНЫЕ ПРОЦЕССЫ В РДС-КРИСТАЛЛЕ

Рассмотрим 4 плоские монохроматические моды с частотами ${{\omega }_{o}},$ ${{\omega }_{e}},$ $2{{\omega }_{e}},$ $3{{\omega }_{e}}$ и характеризуемые операторами уничтожения (рождения) фотона: ${{\hat {a}}_{{1o}}}~\left( {\hat {a}_{{1o}}^{ + }} \right),$ $\hat {a}{{~}_{{1e}}}\left( {\hat {a}_{{1e}}^{ + }} \right),$ $\hat {a}_{{2e}}^{{}}~\left( {\hat {a}_{{2e}}^{ + }} \right)$ и $\hat {a}{{~}_{{3e}}}\left( {\hat {a}_{{3e}}^{ + }} \right).$ Эти моды коллинеарно распространяются внутри РДС-кристалла с квадратичной нелинейностью. Операторы удовлетворяют стандартным коммутационным соотношениям: $\left[ {{{{\hat {a}}}_{{jp}}},\hat {a}_{{kp}}^{ + }} \right] = {{\delta }_{{jp,kp}}}$ ($j,k = 1,2,3;~p = o,e$). Одновременно происходят два процесса: параметрический процесс (тип II) и преобразование частоты вверх за счет суммирования частот субгармоник с частотой накачки [8]:

где ${{k}_{{jp}}}$ – абсолютные значения волновых векторов мод с частотами ${{\omega }_{{jp}}};$ $\Delta {{k}_{q}}$ – волновые расстройки соответствующих процессов для однородного кристалла; $q = 1,2;$ ${{m}_{q}} = \pm 1, \pm 3, \pm 5, \cdots $ – порядки квазисинхронизма; ${{G}_{q}} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {{{{\Lambda }}_{q}}}}} \right. \kern-0em} {{{{\Lambda }}_{q}}}}$ – волновое число (модуль “псевдовектора” решетки доменной структуры с периодом ${{{\Lambda }}_{q}}$). Выполнение условия квазисинхронизма для процессов (1а), (1б) соответствует $\delta {{k}_{q}} = 0.$ Одновременный квазисинхронизм в одной и той же доменной структуре $G = {{G}_{1}} = {{G}_{2}}$ для двух (1а), (1б) процессов можно реализовать, например, при различных порядках квазисинхронизма m_q или при разных длинах когерентности ${{L}_{q}} = {\pi \mathord{\left/ {\vphantom {\pi {\Delta {{k}_{q}}}}} \right. \kern-0em} {\Delta {{k}_{q}}}} = {{{{{\Lambda }}_{q}}} \mathord{\left/ {\vphantom {{{{{\Lambda }}_{q}}} {2{{m}_{q}}}}} \right. \kern-0em} {2{{m}_{q}}}}$ в РДС-кристалле LiNbO₃ [8].

Гамильтониан взаимодействия рассматриваемых процессов имеет вид [8]:

где $\hbar $ – постоянная Планка, ${{\gamma }_{{1,2}}}$ – коэффициенты нелинейного взаимодействия, э.с. – эрмитово сопряжение. Это приближение плоских монохроматических мод при коллинеарном взаимодействии. Поперечная пространственная структура пучков при этом полагается однородной.

Операторные уравнения движения по длине взаимодействия $z$ внутри РДС-кристалла в представлении Гейзенберга описываются динамическим уравнением

Введем безразмерные нелинейные коэффициенты связи ξ = ${{{{\gamma }_{2}}} \mathord{\left/ {\vphantom {{{{\gamma }_{2}}} {{{\gamma }_{1}}}}} \right. \kern-0em} {{{\gamma }_{1}}}}.$ Тогда гамильтониан взаимодействия (2) примет следующий вид:

Введем приведенную длину взаимодействия $\zeta = {{\gamma }_{1}}z,$ диагонализируем гамильтониан взаимодействия (4) методом [9, 10] и найдем его собственные векторы и собственные значения.

СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОЛЯРИЗАЦИОННЫХ МОД

Для изучения поляризационных характеристик ортогональных мод 1о и 1е вычисляются, как это принято [1–6, 8, 11, 12], значения среднего числа фотонов

коэффициентов корреляции фотонов между разными модами

среднего значения операторов Стокса

нормированных на $\left\langle {{\Delta }\hat {S}_{0}^{2}\left( \zeta \right)} \right\rangle $ дисперсии операторов Стокса

где, $\left\langle {{\Delta }\hat {S}_{j}^{2}\left( \zeta \right)} \right\rangle $ = $\left\langle {\hat {S}_{j}^{2}\left( \zeta \right)} \right\rangle - \left\langle {{{{\hat {S}}}_{j}}{{{\left( \zeta \right)}}^{2}}} \right\rangle $ и $\left\langle {{\Delta }\hat {S}_{0}^{2}\left( \zeta \right)} \right\rangle $ = = $\left\langle {\hat {S}_{0}^{2}\left( \zeta \right)} \right\rangle - \left\langle {{{{\hat {S}}}_{0}}{{{\left( \zeta \right)}}^{2}}} \right\rangle ,$ степени поляризации взаимодействующих ортогональных мод

Операторы Стокса ${{\hat {S}}_{{0,1,2,3}}}\left( \zeta \right)$ удовлетворяют следующим коммутационным соотношениям:

Соотношение неопределенности для операторов Стокса имеет вид

Расчеты проводили для следующих случаев:

1. $\xi = 0,6$ и при этом на входе $(\zeta = 0)$ РДС-кристалла моды 2е и 3е полагались в вакуумном состоянии $\left| 0 \right\rangle ,$ а накачка $1o,$ $1e$ – в когерентном состоянии со средним числом фотонов $\left| {{{\alpha }_{{1o}}}} \right\rangle = 3$ и $\left| {{{\alpha }_{{1e}}}} \right\rangle = 3$ и фазой ${{\varphi }_{{1o,1e}}} = {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3},$ т.е., $\left| 3 \right\rangle \left| 3 \right\rangle \left| 0 \right\rangle \left| 0 \right\rangle ,$

2. $\xi = 0,6$ и при этом на входе $(\zeta = 0)$ РДС-кристалла моды 2е и 3е полагались в вакуумном состоянии $\left| 0 \right\rangle ,$ а накачка $1o,$ $1e$ – в когерентном состоянии со средним числом фотонов $\left| {{{\alpha }_{{1o}}}} \right\rangle = 2$ и $\left| {{{\alpha }_{{1e}}}} \right\rangle = 3$ и фазой ${{\varphi }_{{1o,1e}}} = {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0em} 3},$ т.е., $\left| 2 \right\rangle \left| 3 \right\rangle \left| 0 \right\rangle \left| 0 \right\rangle .$

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

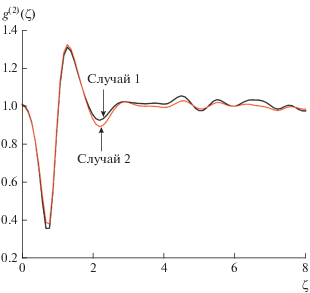
Рис. 1 иллюстрирует динамику значений коэффициентов корреляции или, другими словами, фактора ${{g}^{{\left( 2 \right)}}},$ внутри РДС-кристалла для мод $1o,$ $1e.$ Видно, что кривые ${{g}^{{\left( 2 \right)}}}$ осциллируют по мере возрастания длины взаимодействия и стремятся к значению 1. Для качественной обработки фантомных изображений можно использовать дополнительные поляризационные степени свободы света помимо регистрации фототоков в коррелированных модах $1o,$ $1e,$ как это предложено в [5]. Правда при этом они должны усиливать вакуумные состояния, а не когерентные.

На рис. 2 отображены средние значения операторов Стокса, которые характеризуют состояния поляризации ортогональных мод 1o и 1e. Свет считается полностью неполяризованным, если $\left\langle {{{{\hat {S}}}_{0}}\left( \zeta \right)} \right\rangle > 0~$ [12], и при этом остальные операторы Стокса принимают значения $\left\langle {{{{\hat {S}}}_{{1,2,3}}}\left( \zeta \right)} \right\rangle = 0.$ Он обладает горизонтальной (вертикальной) поляризацией, если значения $\left\langle {{{{\hat {S}}}_{0}}\left( \zeta \right)} \right\rangle > 0,$ $\left\langle {{{{\hat {S}}}_{1}}\left( \zeta \right)} \right\rangle \ne 0,$ и $\left\langle {{{{\hat {S}}}_{{2,3}}}\left( \zeta \right)} \right\rangle = 0.$ У линейно поляризованного света с углом $ + 45^\circ $ $\left( { - 45^\circ } \right)$ значения $\left\langle {{{{\hat {S}}}_{0}}\left( \zeta \right)} \right\rangle > 0,$ $\left\langle {{{{\hat {S}}}_{2}}\left( \zeta \right)} \right\rangle \ne 0,$ $\left\langle {{{{\hat {S}}}_{{1,3}}}\left( \zeta \right)} \right\rangle = 0.$ Для правой или левой круговой поляризации $\left\langle {{{{\hat {S}}}_{0}}\left( \zeta \right)} \right\rangle > 0,$ $\left\langle {{{{\hat {S}}}_{3}}\left( \zeta \right)} \right\rangle \ne 0,$ $\left\langle {{{{\hat {S}}}_{{1,2}}}\left( \zeta \right)} \right\rangle = 0.$

Кривые на рис. 2 демонстрируют преобладание смешанной поляризации. Количественное описание степени поляризации отображено на рис. 4.

На начальном этапе взаимодействия (рис. 3) дисперсия всех четырех нормированных операторов Стокса становится субпуассоновской $\left( {{{{\hat {V}}}_{{0,1,2,3}}} < 1} \right),$ а затем суперпуассоновской $\left( {{{{\hat {V}}}_{{0,2,3}}} > 1} \right).$ При этом, разумеется, не нарушаются соотношения (12)–(14). Одновременно подавление дисперсий всех операторов Стокса было установлено ранее в приближении заданного поля, то есть, когда накачка на частоте $2{{\omega }_{e}}$ полагалась неистощимой, а остальные – в вакуумном состоянии, кроме мод 1o, 1e, которые находились в когерентном состоянии со средним числом фотонов 1 [8] и система уравнений (3) становилась линеаризованной. В данной работе применен более точный метод диагонализации гамильтониана взаимодействия [9, 10]. Он позволяет анализировать квантовые статистические характеристики всех взаимодействующих мод на больших длинах взаимодействии. Отметим, что одновременное подавление дисперсий всех операторов Стокса невозможно в обычном монодоменном кристалле с квадратичной нелинейностью [2, 8], но только в РДС-кристаллах [8]. При этом одновременно должны происходить два и более [8] процессов, например, параметрический (тип II) и преобразование частоты вверх, то есть, фотоны моды 1o процесса (1а) участвуют в процессе (1б).

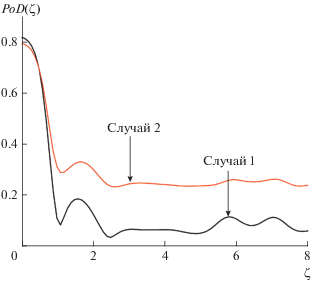
На рис. 4 видно, что степень поляризации стремится к нулю по мере возрастания длины взаимодействия. Ухудшение степени поляризации между модами 1о и 1е возникает за счeт неопределенности разности фаз между ними в процессе распространения внутри нелинейной среды. Из сопоставления случаев 1 и 2 на рис. 4 ясно, что степенью поляризации мод можно управлять дисбалансом входных интенсивностей: уменьшения среднего количества фотонов в одной моде и увеличения в другой. Однако, возможности такого управления ограничены. В любом случае увеличение длины кристалла ведет к деградации квантовой запутанности по поляризациям. Поэтому, учитывая полученные нами результаты, необходимо работать с как можно более тонкими кристаллами.

Работа выполнена при поддержке РФФИ (грант № 18-01-00598а).