1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 84, № 1, 2020

Известия РАН. Серия физическая, 2020, T. 84, № 1, стр. 16-20

Исследование динамики интенсивных импульсов, распространяющихся в фотонно-кристаллическом оптическом волокне с градиентом дисперсии групповой скорости

В. А. Халяпин 1,  2, *

1 Федеральное государственное автономное образовательное учреждение высшего образования “Балтийский федеральный университет имени Иммануила Канта”
Калининград, Россия

2 Федеральное государственное бюджетное образовательное учреждение высшего образования “Калининградский государственный технический университет”
Калининград, Россия

* E-mail: slavasxi@gmail.com

Поступила в редакцию 29.07.2019
После доработки 30.08.2019
Принята к публикации 27.09.2019

Полный текст (PDF)

Аннотация

Аналитически исследована динамика солитоно-подобных импульсов, распространяющихся в волокне с градиентом коэффициента дисперсии групповой скорости в режиме туннельной ионизации и вынужденного комбинационного саморассеяния. Показано, что при определенных условиях возможна взаимная компенсация этих эффектов, которая приводит к стабилизации сигнала.

ВВЕДЕНИЕ

В последние годы значительное внимание привлекают новые фотонно-кристаллические волокна (ФКВ) “кагоме” типа с полой сердцевиной, заполненной газом [1–3], которые позволяют на несколько порядков увеличить мощность вводимого в них излучения, уменьшить потери и нелинейные эффекты. Такие волокна имеют широкую полосу пропускания, включающую всю видимую и инфракрасную области спектра и низкую аномальную дисперсию групповой скорости для широкого спектрального диапазона.

В работе [4] было показано, что ионизация приводит к тому, что спектр импульса смещается в сторону высоких частот, а его длительность уменьшается. Это вызвано тем, что возникающие за счет ионизации свободные электроны вносят отрицательный вклад в показатель преломления [4–12]. Этот эффект противоположен вынужденному комбинационному саморассеянию (ВКС), которое вызывает красное смещение спектра сигнала и увеличение его длительности [13–19]. Известно, что компенсировать уширение импульса и красное смещение, обусловленное ВКС можно, изменив коэффициент групповой дисперсии вдоль волновода [20]. Это достигается с помощью уменьшения диаметра его сердцевины [21, 22]. Первоначально этот подход был предложен для стабилизации сигналов в поглощающей среде [23], а в дальнейшем и для компрессии импульсов [24].

Уравнение, описывающее распространение импульсов с учетом ВКС и туннельной ионизации в ФКВ “кагоме” типа было получено в работах [8, 9]. С помощью теории возмущений [25–27] авторы показали, что при определенных условиях центральная частота солитона может оставаться такой же, какой была на входе в волокно, а импульс может стабилизироваться [28–30]. Целью настоящей работы является исследование влияния градиента коэффициента групповой дисперсии на условие стабилизации и рассмотрение возможности компрессии высокоинтенсивных сигналов в такой среде.

МЕТОД МОМЕНТОВ И СТАБИЛИЗАЦИЯ ДЛИТЕЛЬНОСТИ СИГНАЛА

Динамика световых импульсов, распространяющихся в ФКВ, описывается уравнением [8, 9]

(1)
$\begin{gathered} \frac{{\partial \psi }}{{\partial z}} + \frac{{i{{\beta }_{2}}}}{2}\frac{{{{\partial }^{2}}\psi }}{{\partial {{\tau }^{2}}}} - \frac{{{{\beta }_{3}}}}{6}\frac{{{{\partial }^{3}}\psi }}{{\partial {{\tau }^{3}}}} - i\gamma \psi {{\left| \psi \right|}^{2}} + \\ + \,\,\frac{\gamma }{\omega }\frac{\partial }{{\partial \tau }}\left( {\psi {{{\left| \psi \right|}}^{2}}} \right) + i\gamma {{T}_{R}}\psi \frac{{\partial {{{\left| \psi \right|}}^{2}}}}{{\partial \tau }} + \\ + \,\,i\eta \psi \int\limits_{ - \infty }^{\tau } {\delta \Theta \left( \delta \right)d\tau } = 0. \\ \end{gathered} $

Здесь $\psi $ – медленно меняющаяся огибающая, $z$ – ось, вдоль которой распространяется сигнал, $\tau = {{t - z} \mathord{\left/ {\vphantom {{t - z} {{{\upsilon }_{g}}}}} \right. \kern-0em} {{{\upsilon }_{g}}}}$ – время в сопутствующей системе координат, ${{\upsilon }_{g}}$ – групповая скорость импульса на его центральной частоте $\omega ,$ $\eta $ – коэффициент, характеризующий туннельную ионизацию, $\delta = {{\left| \psi \right|}^{2}} - \left| \psi \right|_{{th}}^{2},$ $\Theta $ – функция Хевисайда, $\left| \psi \right|_{{th}}^{2}$ – величина, пропорциональная пороговой интенсивности туннельной ионизации, ${{\beta }_{2}}$ – коэффициент дисперсии групповой скорости (ДГС), ${{\beta }_{3}}$ – положительный параметр, определяющий дисперсию третьего порядка, $\gamma $ – коэффициент кубической нелинейности, ${{T}_{R}}$ – характеризует вклад ВКС. Коэффициент ${{\beta }_{2}}$ положителен, если центральная частота импульса лежит в области нормальной дисперсии групповой скорости и отрицателен в противоположном случае [31]. В уравнении (1) мы пренебрегли поглощением волновода и потерями, связанными с ионизацией. Это обуславливается тем, что волноводные потери для фундаментальной моды имеют порядок 1 Дб/м и вблизи порога туннельной ионизации нелинейное поглощение мало. Авторами работ [8, 9] для таких импульсов было введено название “floating soliton”.

Медленно меняющаяся огибающая связана с электрическим полем импульса E соотношением

(2)
$E(z,\tau ) = \frac{1}{2}\psi (z,\tau )\exp \left[ { - i\left( {\omega t - kz} \right)} \right] + {\text{c}}{\text{.c}}.,$
где $k$ – волновое число. Анализ динамики параметров импульса проводился на основе метода моментов [17, 32–34]. В работе рассматривался случай солитонного распространения, когда огибающая импульса сохраняет форму гиперболического секанса [17]
(3)
$\begin{gathered} \psi = B\operatorname{sech} \left( {\frac{{\tau - T}}{{{{\tau }_{p}}}}} \right) \times \\ \times \,\,\exp \left[ {i\left( {\phi + \Omega \left( {\tau - T} \right) - C\frac{{{{{\left( {\tau - T} \right)}}^{2}}}}{{2\tau _{p}^{2}}}} \right)} \right], \\ \end{gathered} $
где $B$ – амплитуда сигналаis, ${{\tau }_{p}}$ – его длительность, $C - $ параметр, определяющий частотную модуляцию, $T$ – временное запаздывание, $\phi $ – фаза и $\Omega $ – смещение центральной частоты сигнала. Все параметры зависят от координаты $z.$ Определим моменты импульса, следуя работе [17] в виде
(4)
$E = \int\limits_{ - \infty }^\infty {{{{\left| \psi \right|}}^{2}}d\tau } ,$
(5)
$\tilde {C} = \frac{i}{{2E}}\int\limits_{ - \infty }^\infty {\left( {\tau - T} \right)\left( {\psi {\text{*}}\frac{{\partial \psi }}{{\partial \tau }} - \psi \frac{{\partial \psi {\text{*}}}}{{\partial \tau }}} \right)d\tau } ,$
(6)
${{\sigma }^{2}} = \frac{1}{E}\int\limits_{ - \infty }^\infty {{{{\left( {\tau - T} \right)}}^{2}}{{{\left| \psi \right|}}^{2}}d\tau } ,$
(7)
$T = \frac{1}{E}\int\limits_{ - \infty }^\infty {\tau {{{\left| \psi \right|}}^{2}}d\tau } ,$
(8)
$\Omega = - \frac{i}{{2E}}\int\limits_{ - \infty }^\infty {\left( {{\psi *}\frac{{\partial \psi }}{{\partial \tau }} - \psi \frac{{\partial {\psi *}}}{{\partial \tau }}} \right)d\tau } ,$
где $E$ – параметр, пропорциональный числу фотонов, $\tau _{p}^{2} = {{12{{\sigma }^{2}}} \mathord{\left/ {\vphantom {{12{{\sigma }^{2}}} {{{\pi }^{2}}}}} \right. \kern-0em} {{{\pi }^{2}}}},$ $C = {{12\tilde {С}} \mathord{\left/ {\vphantom {{12\tilde {С}} {{{\pi }^{2}}}}} \right. \kern-0em} {{{\pi }^{2}}}}$ [17]. Дифференцируя (4)–(8) по координате $z$ и используя (1), получаем систему уравнений

(9)
$\frac{{dE}}{{dz}} = 0,$
(10)
$\begin{gathered} \frac{{d\Omega }}{{dz}} = \frac{{{{T}_{R}}\gamma }}{E}\int\limits_{ - \infty }^\infty {{{{\left( {\frac{{\partial {{{\left| \psi \right|}}^{2}}}}{{\partial \tau }}} \right)}}^{2}}d\tau + \frac{{i\gamma }}{{E\omega }}\int\limits_{ - \infty }^\infty {\left( {{\psi *}\frac{{\partial \psi }}{{\partial \tau }} - \psi \frac{{\partial {\psi *}}}{{\partial \tau }}} \right)} } \times \\ \times \,\,\frac{{\partial {{{\left| \psi \right|}}^{2}}}}{{\partial \tau }}d\tau - \frac{\eta }{E}\int\limits_{ - \infty }^\infty {{{{\left| \psi \right|}}^{2}}\delta \Theta \left( \delta \right)d\tau } , \\ \end{gathered} $
(11)
$\frac{{dT}}{{dz}} = - {{\beta }_{2}}\Omega + \frac{{{{\beta }_{3}}}}{{2E}}{{\int\limits_{ - \infty }^\infty {\left| {\frac{{\partial \psi }}{{\partial \tau }}} \right|} }^{2}}d\tau + \frac{{3\gamma }}{{2E\omega }}\int\limits_{ - \infty }^\infty {{{{\left| \psi \right|}}^{4}}} d\tau ,$
(12)
$\frac{{d{{\sigma }^{2}}}}{{dz}} = 2{{\beta }_{2}}\tilde {C} + \frac{{{{\beta }_{3}}}}{E}{{\int\limits_{ - \infty }^\infty {\left( {\tau - T} \right)\left| {\frac{{\partial \psi }}{{\partial t}}} \right|} }^{2}}d\tau ,$
(13)
$\begin{gathered} \frac{{d\tilde {C}}}{{dz}} = \Omega \frac{{dT}}{{dz}} + \frac{{{{\beta }_{2}}}}{E}{{\int\limits_{ - \infty }^\infty {\left| {\frac{{\partial \psi }}{{\partial t}}} \right|} }^{2}}d\tau + \frac{{i{{\beta }_{3}}}}{{4E}} \times \\ \times \,\,\int\limits_{ - \infty }^\infty {\left( {\frac{{{{\partial }^{2}}\psi }}{{\partial {{\tau }^{2}}}}\frac{{\partial {\psi *}}}{{\partial \tau }} - \frac{{{{\partial }^{2}}{\psi *}}}{{\partial {{\tau }^{2}}}}\frac{{\partial \psi }}{{\partial \tau }}} \right)} d\tau + \frac{\gamma }{{2E}}\int\limits_{ - \infty }^\infty {{{{\left| \psi \right|}}^{4}}d\tau } - \\ - \,\,\frac{{i\gamma }}{{E\omega }}\int\limits_{ - \infty }^\infty {\left( {\tau - T} \right)} \frac{{\partial {{{\left| \psi \right|}}^{2}}}}{{\partial \tau }}\left( {{\psi *}\frac{{\partial \psi }}{{\partial \tau }} - \psi \frac{{\partial {\psi *}}}{{\partial \tau }}} \right)d\tau - \\ - \,\,\frac{{i\gamma }}{{2E\omega }}\int\limits_0^\infty {{{{\left| \psi \right|}}^{2}}\left( {\psi \frac{{\partial {\psi *}}}{{\partial \tau }} - {\psi *}\frac{{\partial \psi }}{{\partial \tau }}} \right)} d\tau - \\ - \,\,\frac{{\gamma {{T}_{R}}}}{E}{{\int\limits_{ - \infty }^\infty {\left( {\tau - T} \right)\left( {\frac{{\partial {{{\left| \psi \right|}}^{2}}}}{{\partial \tau }}} \right)} }^{2}}d\tau . \\ \end{gathered} $

Уравнение, определяющее динамику фазы $\phi $ можно записать в неявном виде

(14)
$\begin{gathered} \int\limits_{ - \infty }^\infty {\left( {{\psi *}\frac{{\partial \psi }}{{\partial z}} - \psi \frac{{\partial {\psi *}}}{{\partial z}}} \right.} - i{{\beta }_{2}}{{\left| {\frac{{\partial \psi }}{{\partial \tau }}} \right|}^{2}} - \\ - \,\,\frac{{{{\beta }_{3}}}}{6}\left( {{\psi *}\frac{{{{\partial }^{3}}\psi }}{{\partial {{\tau }^{3}}}} - \psi \frac{{{{\partial }^{3}}{\psi *}}}{{\partial {{\tau }^{3}}}}} \right) - 2i\gamma {{\left| \psi \right|}^{4}} + \\ + \,\,2i\eta {{\left| \psi \right|}^{2}}\int\limits_{ - \infty }^{\tau } {\delta \Theta \left( \delta \right)d\tau {\kern 1pt} '} + \frac{\gamma }{\omega }{{\left| \psi \right|}^{2}} \times \\ \left. { \times \,\,\left( {{\psi *}\frac{{\partial \psi }}{{\partial \tau }} - \psi \frac{{\partial {\psi *}}}{{\partial \tau }}} \right)} \right)d\tau = 0. \\ \end{gathered} $

Подставляя пробную функцию (3) в (9)–(13) и интегрируя по $\tau $, получаем систему уравнений для параметров импульса

(15)
$E = 2{{\tau }_{p}}{{B}^{2}} = {\text{const}},$
(16)
$\frac{{d\Omega }}{{dz}} = \frac{{4\gamma E}}{{15\tau _{p}^{3}}}\left( {{{T}_{R}} - \frac{{5C}}{{4\omega }}} \right) - \frac{{\eta E}}{{3{{\tau }_{p}}}}{{\left( {1 - \frac{{\psi _{{th}}^{2}}}{{{{B}^{2}}}}} \right)}^{{3/2}}},$
(17)
$\frac{{dT}}{{dz}} = - {{\beta }_{2}}\Omega + \frac{{{{\beta }_{3}}}}{2}\left( {\frac{{\left( {{{1 + {{\pi }^{2}}{{C}^{2}}} \mathord{\left/ {\vphantom {{1 + {{\pi }^{2}}{{C}^{2}}} 4}} \right. \kern-0em} 4}} \right)}}{{3\tau _{p}^{2}}} + {{\Omega }^{2}}} \right) + \frac{{\gamma E}}{{2\omega {{\tau }_{p}}}},$
(18)
$\frac{{d\tau _{p}^{2}}}{{dz}} = 2C\left( {{{\beta }_{2}} - {{\beta }_{3}}\Omega } \right),$
(19)
$\frac{{dС}}{{dz}} = \left( {{{\beta }_{2}} - {{\beta }_{3}}\Omega } \right)\left( {\frac{{{4 \mathord{\left/ {\vphantom {4 {{{\pi }^{2}}}}} \right. \kern-0em} {{{\pi }^{2}}}} + {{С}^{2}}}}{{\tau _{p}^{2}}}} \right) + \frac{{2\gamma E}}{{{{\pi }^{2}}{{\tau }_{p}}}}\left( {1 - \frac{\Omega }{\omega }} \right).$

Уравнение для фазы не приводится, поскольку она не играет роли в дальнейшем анализе. Из (15) следует соотношение между амплитудой и длительностью

(20)
$E = 2{{\tau }_{0}}B_{0}^{2} = 2{{\tau }_{{th}}}\psi _{{th}}^{2}.$
Здесь ${{\tau }_{{th}}} - $длительность солитоноподобного импульса, соответствующая амплитуде ${{\psi }_{{th}}}.$

В данной работе мы рассматриваем случай распространения в волноводе с уменьшающимся диаметром сердцевины так, что групповая дисперсия описывается функцией [20]

(21)
$\left| {{{\beta }_{2}}} \right| = \left| {{{\beta }_{{20}}}} \right|\left( {{{1 - z} \mathord{\left/ {\vphantom {{1 - z} L}} \right. \kern-0em} L}} \right),$
где $\left| {{{\beta }_{{20}}}} \right| - $ коэффициент групповой дисперсии на входе в волокно, $L$ – характерная длина изменения ${{\beta }_{2}}.$

Будем искать эволюцию параметров ${{\tau }_{p}}$ и $\Omega $ с помощью метода последовательных приближений. Используя (18) и полагая производную от $C$ нулю, из (19) получаем

(22)
$\Omega = \frac{{\left| {{{\beta }_{2}}} \right|}}{{{{\beta }_{3}}}}\left( {\frac{{\gamma {{\tau }_{p}}E}}{{2\left| {{{\beta }_{2}}} \right|}} - 1} \right).$

Поскольку на входе в среду смещение центральной частоты равно нулю $\left( {{{\Omega }_{0}} = 0} \right),$ то из (22) следует, что $E$ соответствует известной величине для солитона нелинейного уравнения Шредингера $E = {{2\left| {{{\beta }_{{20}}}} \right|} \mathord{\left/ {\vphantom {{2\left| {{{\beta }_{{20}}}} \right|} {\gamma {{\tau }_{0}}}}} \right. \kern-0em} {\gamma {{\tau }_{0}}}}.$ Здесь ${{\tau }_{0}}$ – начальное значение длительности сигнала. Подставляя (21), (22) в (16) и пренебрегая производной нелинейности, получаем уравнение для безразмерной длительности сигнала $u = {{{{\tau }_{p}}} \mathord{\left/ {\vphantom {{{{\tau }_{p}}} {{{\tau }_{0}}}}} \right. \kern-0em} {{{\tau }_{0}}}}$

(23)
${{u}^{3}}\frac{{du}}{{d\zeta }} = \frac{L}{{{{L}_{R}}}} - \frac{L}{{{{L}_{\eta }}}}{{u}^{2}}{{\left( {1 - \frac{u}{{{{u}_{{th}}}}}} \right)}^{{3/2}}} - {{u}^{3}},$
где ${{L}_{R}} = {{15\tau _{0}^{4}} \mathord{\left/ {\vphantom {{15\tau _{0}^{4}} {8{{\beta }_{3}}{{T}_{R}}}}} \right. \kern-0em} {8{{\beta }_{3}}{{T}_{R}}}},$ ${{L}_{\eta }} = {{3\gamma \tau _{0}^{2}} \mathord{\left/ {\vphantom {{3\gamma \tau _{0}^{2}} {2\eta {{\beta }_{3}}}}} \right. \kern-0em} {2\eta {{\beta }_{3}}}}$ – характерные длины ВКС и туннельной ионизации соответственно, $\zeta = {z \mathord{\left/ {\vphantom {z L}} \right. \kern-0em} L}$ – безразмерная длина, ${{u}_{{th}}} = {{{{\tau }_{{th}}}} \mathord{\left/ {\vphantom {{{{\tau }_{{th}}}} {{{\tau }_{0}}}}} \right. \kern-0em} {{{\tau }_{0}}}}.$ Стационарное решение уравнения (23) возможно при условии равенства нулю его правой части.

Рассмотрим сперва динамику длительности интенсивного импульса, испытывающего ионизацию в волноводе без градиента групповой дисперсии [29]

(24)
${{u}^{3}}\frac{{du}}{{d\zeta }} = \frac{L}{{{{L}_{R}}}} - \frac{L}{{{{L}_{\eta }}}}{{u}^{2}}{{\left( {1 - \frac{u}{{{{u}_{{th}}}}}} \right)}^{{3/2}}}.$

Уравнение (24) имеет стационарное решение при условии ${{L}_{R}} > {{L}_{\eta }}{{\left( {{7 \mathord{\left/ {\vphantom {7 {4{{u}_{{th}}}}}} \right. \kern-0em} {4{{u}_{{th}}}}}} \right)}^{2}}{{\left( {7{\text{/}}3} \right)}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}.$ Это неравенство можно переписать в виде

(25)
${{\tau }_{0}} < \frac{{2\sqrt 5 }}{7}{{\left( {\frac{3}{7}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}}\frac{{\left| {{{\beta }_{2}}} \right|}}{{\gamma \psi _{{th}}^{2}}}\sqrt {\frac{\eta }{{\gamma {{T}_{R}}}}} .$

Используя метод последовательных приближений, находим два корня, соответствующих нулю правой части (24)

(26)
${{u}_{1}} \approx \sqrt {\frac{{{{L}_{\eta }}}}{{{{L}_{R}}}}} {{\left( {1 - \frac{1}{{{{u}_{{th}}}}}\sqrt {\frac{{{{L}_{\eta }}}}{{{{L}_{R}}}}} } \right)}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 4}} \right. \kern-0em} 4}}}},$
(27)
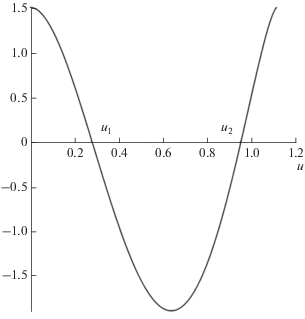
${{u}_{2}} \approx {{u}_{{th}}}\left( {1 - {{{\left( {\frac{1}{{{{u}_{{th}}}}}\sqrt {\frac{{{{L}_{\eta }}}}{{{{L}_{R}}}}} } \right)}}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}} \right).$

Из рис. 1 и уравнения (24) видно, что ${{u}_{1}}$ – точка устойчивого равновесия, а ${{u}_{2}}$ – неустойчивого. Это означает, что если ${{u}_{2}} > 1,$ то длительность импульса уменьшается вплоть до значения ${{u}_{1}}.$ В противном случае длительность сигнала будет увеличиваться, минуя режим стабилизации.

Рис. 1.

График правой части уравнения (24) для значений параметров ${{{{L}_{\eta }}} \mathord{\left/ {\vphantom {{{{L}_{\eta }}} {{{L}_{R}}}}} \right. \kern-0em} {{{L}_{R}}}} = 0.05,$ ${1 \mathord{\left/ {\vphantom {1 {{{u}_{{th}}}}}} \right. \kern-0em} {{{u}_{{th}}}}} = 0.9,$ ${{u}_{1}}$ – точка стабилизации сигнала.

Рассмотрим теперь другой режим, соответствующий распространению сигнала в градиентном волноводе с интенсивностью ниже пороговой интенсивности туннельной ионизации. В этом случае ионизацией можно пренебречь и уравнение (23) принимает вид

(28)
${{u}^{3}}\frac{{du}}{{d\zeta }} = \frac{L}{{{{L}_{R}}}} - {{u}^{3}}.$

Легко видеть, что точка стабилизации определяется выражением [20]

(29)
${{u}_{3}} = \sqrt[3]{{\frac{L}{{{{L}_{R}}}}}}.$

Также несложно получить аналитическое решение (28). Соответствующее смещение частоты определяется из (22). Заметим, что для волновода без градиента дисперсии (последнего слагаемого в правой части (29)) можно получить решения для длительности и смещения частоты в виде [20, 32, 35]

(30)
${{\tau }_{p}} = {{\tau }_{0}}{{\left( {1 + \frac{{4z}}{{{{L}_{R}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}},$
(31)
$\Omega = \frac{{\left| {{{\beta }_{2}}} \right|}}{{{{\beta }_{3}}}}\left( {{{{\left( {1 + \frac{{4z}}{{{{L}_{R}}}}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}} - 1} \right).$

Известную формулу Гордона [15], описывающую смещение частоты солитона при ВКС, можно получить из (31), используя приближение ${z \mathord{\left/ {\vphantom {z {{{L}_{R}}}}} \right. \kern-0em} {{{L}_{R}}}} < 1.$

Если интенсивность импульса в процессе его компрессии становится больше пороговой интенсивности туннельной ионизации (или $u < {{u}_{{th}}}$ см. (20)), то стационарное решение можно найти, приравняв правую часть (23) к нулю.

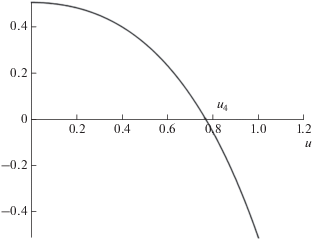
Рассмотрим режим, когда $L < {{L}_{\eta }}$ и правая часть (23) имеет одну стационарную точку, которая является точкой устойчивого равновесия рис. 2. Здесь основной вклад дают слагаемые, описывающее ВКС и градиент групповой дисперсии. Ионизационную поправку можно учесть с помощью метода последовательных приближений, отталкиваясь от (29). Таким образом, в первом приближении получаем выражение для точки устойчивого равновесия

(32)
${{u}_{4}} = \sqrt[3]{{\frac{L}{{{{L}_{R}}}} - \frac{L}{{{{L}_{\eta }}}}{{{\left( {\frac{L}{{{{L}_{R}}}}} \right)}}^{2}}{{{\left( {1 - \frac{L}{{{{u}_{{th}}}{{L}_{R}}}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}.$
Рис. 2.

Правая часть уравнения (23) в случае одного корня ${{u}_{4}},$ определяемого формулой (32) для значений параметров ${L \mathord{\left/ {\vphantom {L {{{L}_{\eta }}}}} \right. \kern-0em} {{{L}_{\eta }}}} = 0.5,$ ${L \mathord{\left/ {\vphantom {L {{{L}_{R}}}}} \right. \kern-0em} {{{L}_{R}}}} = 0.5,$ ${1 \mathord{\left/ {\vphantom {1 {{{u}_{{th}}}}}} \right. \kern-0em} {{{u}_{{th}}}}} = 0.9.$

Если же $L > {{L}_{\eta }}$ и правая часть (23) имеет два корня, то для стационарных точек находим приближенные выражения

(33)
${{u}_{5}} = \sqrt {\frac{{{L \mathord{\left/ {\vphantom {L {{{L}_{R}}}}} \right. \kern-0em} {{{L}_{R}}}} - {{{\left( {{{{{L}_{\eta }}} \mathord{\left/ {\vphantom {{{{L}_{\eta }}} {{{L}_{R}}}}} \right. \kern-0em} {{{L}_{R}}}}} \right)}}^{3}}}}{{{{{\left( {{{1 - {{L}_{\eta }}} \mathord{\left/ {\vphantom {{1 - {{L}_{\eta }}} {{{u}_{{th}}}{{L}_{R}}}}} \right. \kern-0em} {{{u}_{{th}}}{{L}_{R}}}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{L \mathord{\left/ {\vphantom {L {{{L}_{\eta }}}}} \right. \kern-0em} {{{L}_{\eta }}}}}}} ,$
(34)
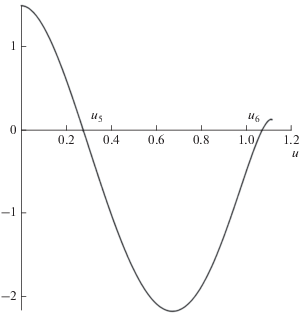
${{u}_{6}} = {{u}_{{th}}}\left( {1 - {{{\left( {\frac{{{{L}_{\eta }}}}{{Lu_{{th}}^{2}}}\left( {\frac{L}{{{{L}_{R}}}} - u_{{th}}^{3}} \right)} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}} \right).$

Значение ${{u}_{5}}$ является точкой устойчивого равновесия рис 3. Таким образом, формулы (33), (34) являются обобщением (26), (27), а (32) обобщает (29) на случай линейно уменьшающегося коэффициента групповой дисперсии.

Рис. 3.

Правая часть уравнения (23) в случае двух корней ${{u}_{5}},$ ${{u}_{6}}$ для значений параметров ${L \mathord{\left/ {\vphantom {L {{{L}_{\eta }}}}} \right. \kern-0em} {{{L}_{\eta }}}} = 30,$ ${L \mathord{\left/ {\vphantom {L {{{L}_{R}}}}} \right. \kern-0em} {{{L}_{R}}}} = 1.5,$ ${1 \mathord{\left/ {\vphantom {1 {{{u}_{{th}}}}}} \right. \kern-0em} {{{u}_{{th}}}}} = 0.9.$

ЗАКЛЮЧЕНИЕ

В работе рассмотрен случай распространения светового импульса в режиме ВКС и туннельной ионизации с учетом градиента коэффициента групповой дисперсии вдоль оси волновода. Известно, что ВКС вызывает красное смещение и временное уширение сигнала. Стабилизировать такой импульс [20] или подвергнуть компрессии [24] можно, сужая диаметр сердцевины волновода, что ведет к уменьшению групповой дисперсии. На основе метода моментов было проведено аналитическое исследование динамики интенсивных солитоноподобных импульсов, вызывающих ионизацию, и найдены условия, при которых импульс будет стабилизироваться. Полученные результаты можно применять для осуществления каскадной компрессии. На первом этапе солитоноподобный импульс за счет градиента групповой дисперсии входит в область, в которой относительная длительность сигнала лежит ниже значения ${{u}_{2}},$ определяемого (27). На втором этапе можно использовать волокно с постоянным диаметром, а компрессия будет происходить уже за счет ионизации до значения стабилизации ${{u}_{1}}$ см. (26). Следует отметить, что поглощение, неизбежно сопровождающее ионизацию, приведет к тому, что стабилизация будет носить временный характер. Учет динамики сигнала с учетом потерь волноводных и нелинейных потерь требует отдельного рассмотрения.

Работа выполнена при финансовой поддержке РФФИ (проект № 19-02-00234а).

Список литературы

  1. Couny F., Benabid F., Light P.S. // Opt. Lett. 2006. V. 31. P. 3574.

  2. Couny F., Roberts P.J., Birks T.A. et al. // Opt. Expr. 2008. V. 16. P. 20626.

  3. Couny F., Benabid F., Roberts P.J. et al. // Science. 2007. V. 318. P. 1118.

  4. Serebryannikov E.E., Zheltikov A.M. // Phys. Rev. A. 2007. V. 76. Art. № 013820.

  5. Wood W.M., Siders C.W., Downer M.C. // Phys. Rev. Lett. 1991. V. 67. P. 3523.

  6. Wilks S.C., Dawson J.M., Mori W.B. // Phys. Rev. Lett. 1988. V. 61. P. 337.

  7. Yablonovitch E. // Phys. Rev. A. 1974. V. 10. P. 1888.

  8. Hölzer P., Chang W., Travers J.C. et al. // Phys. Rev. Lett. 2011. V. 107. Art. № 203902.

  9. Hölzer P., Chang W., Travers J.C. et al. // Phys. Rev. Lett. 2011. V. 107. Art. № 203901.

  10. Saleh M.F., Biancalana F. // Phys. Rev. A. 2011. V. 84. Art. № 063838.

  11. Facão M., Carvalho M.I., Almeida P. // Phys. Rev. A. 2013. V. 87. Art. № 063803.

  12. Facão M., Carvalho M.I. // Appl. Phys. B. 2014. V. 116. P. 353.

  13. Дианов Е.М., Карасик А.Я., Мамышев П.В. и др. // Письма в ЖЭТФ. 1985. Т. 41. № 6. С. 242; Dia-nov E.M., Karasik A.Ya., Mamyshev P.V. et al. // JETP Lett. 1985. V. 41. № 6. P. 294.

  14. Mitschke F.M., Mollenauer L.F. // Opt. Lett. 1986. V. 11. P. 659.

  15. Gordon J.P. // Opt. Lett. 1986. V. 11. P. 662.

  16. Agrawal G.P. Nonlinear fiber optics. N.Y.: Academic, 2007.

  17. Santhanam J., Agraval G. // Opt. Commun. 2003. V. 222. P. 413.

  18. Bugay A.N., Khalyapin V.A. // Phys. Lett. A. 2017. V. 381. № 4. P. 399.

  19. Бугай А.Н., Халяпин В.А. // Опт. и спектроск. 2017. Т. 123. № 2. С. 171; Bugay A.N., Khalyapin V.A. // Opt. Spectrosс. 2017. V. 123. № 2. P. 181.

  20. Chernikov S.V., Mamyshev P.V. // J. Opt. Soc. Am. B. 1991. V. 8. № 8. P. 1633.

  21. Murata H., Inagaki N. // IEEE J. Quant. Electron. 1981. V. 17. P. 835.

  22. Bogatyrjov V.A., Bubnov M.M., Dianov E.M. et al. // Pure Appl. Opt. 1995. V. 4. P. 345.

  23. Tajima K. // Opt. Lett. 1987. V. 12. P. 54.

  24. Gérôme F., Cook K., George A.K. et al. // Opt. Expr. 2007. V. 15. № 12. P. 7126.

  25. Serkin V.N., Vysloukh V.A. // Wave Phenom. Techn. Digest. Opt. Soc. Am. 1993. V. 15. P. 236.

  26. Serkin V.N., Vysloukh V.A., Taylor J.R. // Electron. Lett. 1993. V. 29. P. 12.

  27. Серкин В.Н., Беляева Т.Л., Корро Г.Х. и др. // Квант. электрон. 2003. Т. 33. С. 325; Serkin V.N., Belyaeva T.L., Corro G.H. et al. // Quant. Electron. 2003. V. 33. P. 325.

  28. Bugay A.N., Khalyapin V.A. // Commun. Nonlin. Sci. Numer. Simulat. 2019. V. 75. P. 270.

  29. Bugay A.N., Khalyapin V.A. // Laser Phys. 2019. V. 29. Art. № 035402.

  30. Халяпин В.А. // Изв. РАН. Сер. физ. 2019. Т. 83. № 1. С. 32; Khalyapin V.A. // Bull. Russ. Acad. Sci. Phys. 2019. V. 83. № 1. P. 24.

  31. Козлов С.А., Сазонов С.В. // ЖЭТФ. 1997. Т. 111. С. 404; Kozlov S.A., Sazonov S.V. // JETP. 1997. V. 84. P. 221.

  32. Tsoy E.N., Sterke C.M. // J. Opt. Soc. Am. B. 2006. V. 23. P. 2425.

  33. Tsoy E.N., Sterke C.M. // Phys. Rev. A. 2007. V. 76. Art. № 043804.

  34. Маймистов А.И. // ЖЭТФ. 1993. Т. 104. С. 3620; Maimistov A.I. // JETP. 1993. V. 77. P. 727.

  35. Ivanov L.M., Branzalov P.P., Pavlov L.I. // Opt. Quant. Electron. 1992. V. 24. P. 565.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал