Известия РАН. Серия физическая, 2020, T. 84, № 1, стр. 11-15

Нелинейная динамика предельно коротких солитонов обобщенной редуцированной системы Максвелла–Блоха

С. В. Сазонов^1, *, Н. В. Устинов¹

¹ Федеральное государственное бюджетное образовательное учреждение высшего образования “Московский государственный университет имени М.В. Ломоносова”
Москва, Россия

^* E-mail: sazonov.sergey@gmail.com

Поступила в редакцию 29.07.2019
После доработки 30.08.2019
Принята к публикации 27.09.2019

DOI: 10.31857/S0367676520010287

Полный текст (PDF)

Аннотация

Без использования приближения медленно меняющейся огибающей проведен учет влияния удаленных квантовых состояний на два выделенных атомных уровня при распространении в среде предельно коротких электромагнитных импульсов. Получено обобщение редуцированной системы Максвелла–Блоха, интегрируемое методом обратной задачи рассеяния. Найдены и исследованы его солитонные и бризерные решения.

ВВЕДЕНИЕ

Одной из тенденций развития лазерной физики является создание в лабораторных условиях оптических импульсов все более коротких длительностей [1–3]. К импульсам, длительность которых составляет порядка одного–двух периодов электромагнитных колебаний, уже неприменимо приближение медленно меняющихся огибающих (ММО). Точнее говоря, здесь даже нельзя говорить об огибающей импульса. В этом случае принято говорить о предельно коротких импульсах (ПКИ).

В работе [4] был, пожалуй, впервые совершен отказ от приближения ММО при альтернативном подходе к описанию явления самоиндуцированной прозрачности в двухуровневой среде. Вместо приближения ММО в [4] было предложено использовать приближение однонаправленного распространения, в котором предполагается, что концентрация n двухуровневых атомов мала. В результате авторы пришли к так называемой редуцированной системе уравнений Максвелла–Блоха (РМБ). Эта система оказалась интегрируемой методом обратной задачи рассеяния (МОЗР) [5–7].

К началу 90-х гг. прошлого столетия назрела необходимость в развитии теоретических методов нелинейной оптики ПКИ в связи с экспериментальными достижениями по их генерации. В работах [8, 9] для описания распространения малопериодного импульса в двухуровневой среде было предложено использовать приближение внезапного возбуждения, основанное на условии

(1)

${{\omega }_{0}}{{\tau }_{p}} \ll 1,$

где ${{\omega }_{0}}$ – частота рассматриваемого квантового перехода, ${{\tau }_{p}}$ – длительность импульса. При этом концентрация атомов не предполагалась малой. В результате исключения материальных переменных для интеграла по времени от электрического поля $E$ импульса было получено знаменитое уравнение синус–Гордона, тоже интегрируемое в рамках МОЗР [6].

Так как спектр ПКИ достаточно широк, во взаимодействие с ним могут вовлекаться много квантовых переходов. Как следствие, приближение двухуровневой среды теряет свою силу. В работах [10, 11] был проведен учет квантовых переходов с рассматриваемых двух уровней на вышележащие квантовые состояния. Эти состояния аппроксимировались двумя дополнительными уровнями с порядковыми номерами 3 и 4. При этом использовалось приближение оптической прозрачности, которое предполагает в рассматриваемом случае выполнение условий

(2)

${{\omega }_{{31}}}{{\tau }_{p}}\sim {{\omega }_{{42}}}{{\tau }_{p}} \gg 1,$

где ${{\omega }_{{31}}}$ и ${{\omega }_{{42}}}$ – частоты переходов $1 \leftrightarrow 3$ и $2 \to 4$ соответственно.

На частоту выделенного перехода между состояниями с порядковыми номерами 1 и 2 накладывалось в [10, 11] условие (1) и, затем, применялось приближение внезапного возбуждения. В результате для интеграла по времени от поля импульса было получено обобщенное уравнение синус–Гордона, которое оказалось интегрируемым с помощью МОЗР [11].

Целью настоящей работы является поиск интегрируемого обобщения системы РМБ при исследовании распространения ПКИ в многоуровневой среде малой атомной концентрации без наложения условия (1).

ОБОБЩЕННАЯ РЕДУЦИРОВАННАЯ СИСТЕМА МАКСВЕЛЛА–БЛОХА

Следуя [10, 11], будем рассматривать четырехуровневую среду. Предполагая концентрацию атомов малой [4], запишем волновое уравнение в редуцированном виде

(3)

$\frac{{\partial E}}{{\partial z}} + \frac{1}{c}\frac{{\partial E}}{{\partial t}} = - \frac{{2\pi }}{c}\frac{{\partial P}}{{\partial t}},$

где $z$ – ось, вдоль которой распространяется импульс, $c$ – скорость света в вакууме, $t$ – время, $P$ – поляризационный отклик среды, определяемый через элементы ${{\rho }_{{{\mu \nu }}}}$ матрицы плотности $\hat {\rho }$ атома и дипольные моменты ${{d}_{{{\mu \nu }}}},$ которые соответствуют разрешенным переходам:

(4)

$\begin{gathered} P = n[{{d}_{{21}}}({{\rho }_{{21}}} + \rho _{{21}}^{ * }) + \\ + \,\,{{d}_{{31}}}({{\rho }_{{31}}} + \rho _{{31}}^{ * }) + {{d}_{{42}}}({{\rho }_{{42}}} + \rho _{{42}}^{ * })]. \\ \end{gathered} $

При этом материальные уравнения имеют вид

(5)

$\frac{{\partial {{\rho }_{{ml}}}}}{{\partial t}} = - i{{\omega }_{{ml}}}{{\rho }_{{ml}}} + \frac{i}{\hbar }E{{\left[ {\hat {d},\hat {\rho }} \right]}_{{ml}}}$

$\left( {m,l = 1,2,3,4} \right),$ где ${{\omega }_{{ml}}}$ – частота перехода $m \leftrightarrow l,$ $\hat {d}$ – матрица дипольного момента, выделяющая разрешенные квантовые переходы:

(6)

$\hat {d} = \left( {\begin{array}{*{20}{c}} 0&0&{{{d}_{{42}}}}&0 \\ 0&0&0&{{{d}_{{31}}}} \\ {{{d}_{{42}}}}&0&0&{{{d}_{{21}}}} \\ 0&{{{d}_{{31}}}}&{{{d}_{{21}}}}&0 \end{array}} \right).$

Системой (3)–(6) определяется исходная физическая модель.

В силу условия (2) в уравнениях (5) для элементов ${{\rho }_{{31}}},$ ${{\rho }_{{42}}},$ ${{\rho }_{{32}}},$ ${{\rho }_{{43}}}$ и ${{\rho }_{{41}}}$ матрицы плотности пренебрежем левыми частями, т.е. положим ${{\partial {{\rho }_{{31}}}} \mathord{\left/ {\vphantom {{\partial {{\rho }_{{31}}}} {\partial t}}} \right. \kern-0em} {\partial t}}$ = ${{\partial {{\rho }_{{42}}}} \mathord{\left/ {\vphantom {{\partial {{\rho }_{{42}}}} {\partial t}}} \right. \kern-0em} {\partial t}}$ = ${{\partial {{\rho }_{{32}}}} \mathord{\left/ {\vphantom {{\partial {{\rho }_{{32}}}} {\partial t}}} \right. \kern-0em} {\partial t}}$ = ${{\partial {{\rho }_{{43}}}} \mathord{\left/ {\vphantom {{\partial {{\rho }_{{43}}}} {\partial t}}} \right. \kern-0em} {\partial t}}$ = ${{\partial {{\rho }_{{41}}}} \mathord{\left/ {\vphantom {{\partial {{\rho }_{{41}}}} {\partial t}}} \right. \kern-0em} {\partial t}} = 0.$ Тогда в предположении, что до импульсного воздействия состояния 3 и 4 не заселены, получим приближенно следующие выражения (подробности см. в [11]):

(7)

${{\rho }_{{31}}} = \frac{{{{d}_{{31}}}E}}{{\hbar {{\omega }_{{31}}}}}{{\rho }_{{11}}},\,\,\,\,{{\rho }_{{42}}} = \frac{{{{d}_{{42}}}E}}{{\hbar {{\omega }_{{42}}}}}{{\rho }_{{22}}},$

(8)

$\begin{gathered} {{\rho }_{{32}}} = \frac{{{{d}_{{31}}}E\rho _{{21}}^{ * }}}{{\hbar {{\omega }_{{32}}}}} \approx \frac{{{{d}_{{31}}}E}}{{\hbar {{\omega }_{{31}}}}}\rho _{{21}}^{ * }, \\ {{\rho }_{{41}}} = \frac{{{{d}_{{42}}}E{{\rho }_{{21}}}}}{{\hbar {{\omega }_{{41}}}}} \approx \frac{{{{d}_{{42}}}E}}{{\hbar {{\omega }_{{42}}}}}{{\rho }_{{21}}}. \\ \end{gathered} $

В соотношениях (8) мы положили приближенно ${{\omega }_{{32}}} \approx {{\omega }_{{31}}}$ и ${{\omega }_{{41}}} \approx {{\omega }_{{42}}}.$

Подставив (8) в уравнение (5) для ${{\rho }_{{21}}},$ найдем

(9)

$\begin{gathered} \frac{{\partial {{\rho }_{{21}}}}}{{\partial t}} = - i\left[ {{{\omega }_{{21}}} + \left( {\frac{{d_{{31}}^{2}}}{{{{\omega }_{{31}}}}} - \frac{{d_{{42}}^{2}}}{{{{\omega }_{{42}}}}}} \right)\frac{{{{E}^{2}}}}{{{{\hbar }^{2}}}}} \right]{{\rho }_{{21}}} + \\ + \,\,i\frac{{{{d}_{{21}}}}}{\hbar }E\left( {{{\rho }_{{11}}} - {{\rho }_{{22}}}} \right). \\ \end{gathered} $

После подстановки выражений (7) в (4) и в уравнение (5) для ${{\rho }_{{11}}}$ имеем

(10)

$P = n\left[ {{{d}_{{21}}}\left( {{{\rho }_{{21}}} + \rho _{{21}}^{ * }} \right) + \frac{{2E}}{\hbar }\left( {\frac{{d_{{31}}^{2}}}{{{{\omega }_{{31}}}}}{{\rho }_{{11}}} + \frac{{d_{{42}}^{2}}}{{{{\omega }_{{42}}}}}{{\rho }_{{22}}}} \right)} \right],$

(11)

$\frac{{\partial {{\rho }_{{11}}}}}{{\partial t}} = - \frac{{\partial {{\rho }_{{22}}}}}{{\partial t}} = i\frac{{{{d}_{{21}}}}}{\hbar }E\left( {{{\rho }_{{21}}} - \rho _{{21}}^{ * }} \right).$

Отсюда следует, что в принятом приближении ${{\rho }_{{11}}} + {{\rho }_{{22}}} = 1.$ Введя вещественные блоховские переменные $W = {{\left( {{{\rho }_{{22}}} - {{\rho }_{{11}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\rho }_{{22}}} - {{\rho }_{{11}}}} \right)} 2}} \right. \kern-0em} 2},$ $U = {{\left( {{{\rho }_{{21}}} + \rho _{{21}}^{ * }} \right)} \mathord{\left/ {\vphantom {{\left( {{{\rho }_{{21}}} + \rho _{{21}}^{ * }} \right)} 2}} \right. \kern-0em} 2}$ и $V = {{ - i\left( {\rho _{{21}}^{ * } - {{\rho }_{{21}}}} \right)} \mathord{\left/ {\vphantom {{ - i\left( {\rho _{{21}}^{ * } - {{\rho }_{{21}}}} \right)} 2}} \right. \kern-0em} 2},$ из уравнений (9)–(11) и (3) получим следующую систему:

(12)

$\frac{{\partial U}}{{\partial \tau }} = - \left( {{{\omega }_{0}} + \beta {{\Omega }^{2}}} \right)V,$

(13)

$\frac{{\partial V}}{{\partial \tau }} = \left( {{{\omega }_{0}} + \beta {{\Omega }^{2}}} \right)U + \Omega W,$

(14)

$\frac{{\partial W}}{{\partial \tau }} = - \Omega V,$

(15)

$\frac{{\partial \Omega }}{{\partial z}} = - \alpha \frac{\partial }{{\partial \tau }}\left( {U - 2\beta \Omega W} \right).$

Здесь использованы обозначения $\tau = {{t - z} \mathord{\left/ {\vphantom {{t - z} {{{v}_{0}}}}} \right. \kern-0em} {{{v}_{0}}}},$ ${{\omega }_{0}} \equiv {{\omega }_{{21}}},$ $\Omega = {{2{{d}_{{21}}}E} \mathord{\left/ {\vphantom {{2{{d}_{{21}}}E} \hbar }} \right. \kern-0em} \hbar };$ постоянные $\alpha ,$ $\beta $ и ${{v}_{0}}$ выражаются через физические параметры рассматриваемой задачи.

Положив $\beta = 0$ в уравнениях (12)–(15), получим хорошо известную систему РМБ, справедливую для системы двухуровневых атомов. Ниже уравнения (12)–(15) будем называть обобщенной системой РМБ (ОРМБ). Подчеркнем, что дипольные моменты разрешенных квантовых переходов могут находиться в различных количественных отношениях друг с другом. Поэтому слагаемые в уравнениях (12), (13) и (15), учитывающие отклонение от модели двухуровневой среды, нельзя рассматривать как всего лишь малые поправки к системе РМБ.

СТОЛКНОВЕНИЯ СОЛИТОНОВ И БРИЗЕРНЫЕ РЕШЕНИЯ

В работах [12–15] рассматривалась системы уравнений эквивалентные модифицированным уравнениям РМБ (МРМБ)

(16)

$\frac{{\partial {{U}_{0}}}}{{\partial T}} = - 2{{\omega }_{0}}\sqrt {1 - {{\varepsilon }^{2}}\Omega _{0}^{2}} {{V}_{0}},$

(17)

$\frac{{\partial {{V}_{0}}}}{{\partial T}} = 2{{\omega }_{0}}\sqrt {1 - {{\varepsilon }^{2}}\Omega _{0}^{2}} {{U}_{0}} + {{\Omega }_{0}}{{W}_{0}},$

(18)

$\frac{{\partial {{W}_{0}}}}{{\partial T}} = - {{\Omega }_{0}}{{V}_{0}},$

(19)

$\frac{{\partial {{\Omega }_{0}}}}{{\partial Z}} = - \frac{1}{{{{\omega }_{0}}}}\frac{{\partial {{U}_{0}}}}{{\partial T}}.$

Эти уравнения интегрируемы с помощью МОЗР и описывают нелинейную динамику двухкомпонентных электромагнитных и акустических ПКИ в анизотропных двухуровневых средах. Различные типы солитонных решений уравнений МРМБ были подробно исследованы [13–15].

Система ОРМБ (12)–(15) тоже оказалась интегрируемой в рамках МОЗР [16] и связана с уравнениями МРМБ (16)–(19) при выполнении условия $\varepsilon = \sqrt {{{ - \beta } \mathord{\left/ {\vphantom {{ - \beta } {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}}} $ посредством замены зависимых и независимых переменных $(T,Z,{{\Omega }_{{\text{0}}}},{{U}_{0}},{{V}_{0}},{{W}_{0}})$ → → $(\tau ,z,\Omega ,U,V,W),$ где

(20)

$\begin{gathered} d\tau = \left( {1 + \sqrt {1 - {{\varepsilon }^{2}}\Omega _{0}^{2}(T,Z)} } \right)dT + 2{{\varepsilon }^{2}}{{W}_{0}}dZ, \\ dz = \frac{{dZ}}{{{{\omega }_{0}}\alpha }},\,\,\,\,\Omega (\tau ,z) = \frac{{{{\Omega }_{0}}(T,Z)}}{{1 + \sqrt {1 - {{\varepsilon }^{2}}\Omega _{0}^{2}(T,Z)} }}, \\ W(\tau ,z) = {{W}_{0}}(T,Z),\,\,\,\,U(\tau ,z) = {{V}_{0}}(T,Z), \\ V(\tau ,z) = - {{U}_{0}}(T,Z). \\ \end{gathered} $

Эта связь позволяет получить решения системы ОРМБ (12)–(15), исходя из известных решений уравнений МРМБ. Рассмотрим различные случаи.

${\text{Случай}}\,\,\,\,\beta < - \frac{1}{{4{{\omega }_{0}}}}.$

Замена переменных (20) не позволяет здесь получить несингулярное решение системы ОРМБ, если использовать односолитонное решение уравнений МРМБ. Однако, к несингулярным решениям приводит бризерное решение уравнение МРМБ. Переменная Ω₀ этого решения записывается без потери общности в виде

(21)

${{\Omega }_{0}} = \frac{1}{{i\sigma }}\frac{\partial }{{\partial T}}\lg \left| {\frac{{{{s}_{ - }}}}{{{{s}_{ + }}}}} \right|,$

где

$\begin{gathered} {{s}_{ \pm }} = {{\nu }_{I}}\left[ {{{r}_{ + }}\exp ( - {{\theta }_{R}}) + {{r}_{ - }}\exp ({{\theta }_{R}})} \right] \pm \\ \pm \,\,i{{\nu }_{R}}\left[ {{{r}_{ + }}\exp ( - i{{\theta }_{I}}) + {{r}_{ - }}\exp (i{{\theta }_{I}})} \right], \\ \end{gathered} $

${{r}_{ \pm }} = \varepsilon ({{\nu }_{I}} - i{{\nu }_{R}}) \pm i\sigma ,$

${{\theta }_{R}} = 2{{\nu }_{R}}\left[ {T - \frac{{W_{0}^{{(0)}}\left( {\nu _{R}^{2} + \nu _{I}^{2} + \omega _{0}^{2}} \right)Z}}{{\nu _{R}^{4} + 2\left( {\nu _{I}^{2} + \omega _{0}^{2}} \right)\nu _{R}^{2} + {{{\left( {\nu _{I}^{2} - \omega _{0}^{2}} \right)}}^{2}}}}} \right],$

${{\theta }_{I}} = 2{{\nu }_{I}}\left[ {T + \frac{{W_{0}^{{(0)}}\left( {\nu _{R}^{2} + \nu _{I}^{2} - \omega _{0}^{2}} \right)Z}}{{\nu _{R}^{4} + 2\left( {\nu _{I}^{2} + \omega _{0}^{2}} \right)\nu _{R}^{2} + {{{\left( {\nu _{I}^{2} - \omega _{0}^{2}} \right)}}^{2}}}}} \right],$

$\sigma = {{\sqrt {1 + 4\beta {{\omega }_{0}}} } \mathord{\left/ {\vphantom {{\sqrt {1 + 4\beta {{\omega }_{0}}} } 2}} \right. \kern-0em} 2},$ ${{\nu }_{R}},$ ${{\nu }_{I}}$ и $W_{0}^{{(0)}}$ – вещественные постоянные.

Подстановка выражения (21) в соотношения (20) дает неявное определение переменной $\Omega $ бризерного решения системы ОРМБ (12)–(15). При этом параметры ${{\nu }_{R}}$ и ${{\nu }_{I}}$ задают длительность и несущую частоту бризера. Если несущая частота велика, то полученный бризер похож на бризер системы РМБ. При уменьшении несущей частоты в центре бризера системы ОРМБ возникает осцилляция заостренной формы, амплитуда которой существенно превышает амплитуды соседних осцилляций.

${\text{Случай}}\,\,\,\, - \frac{1}{{4{{\omega }_{0}}}} < \beta < 0.$

Выражение для переменной ${{\Omega }_{0}}$ односолитонного решения уравнений МРМБ, позволяющее получить несингулярное решение системы ОРМБ, имеет в рассматриваемом случае вид

(22)

${{\Omega }_{0}} = \pm 2\sqrt A \frac{{\operatorname{ch} \theta }}{{A{{{\operatorname{ch} }}^{2}}\theta + {{\varepsilon }^{2}}}},$

где $A = {1 \mathord{\left/ {\vphantom {1 {(4{{\nu }^{2}})}}} \right. \kern-0em} {(4{{\nu }^{2}})}} - {{\varepsilon }^{2}}\left( {{{1 + \omega _{0}^{2}} \mathord{\left/ {\vphantom {{1 + \omega _{0}^{2}} {{{\nu }^{2}}}}} \right. \kern-0em} {{{\nu }^{2}}}}} \right),$ θ = = $2\nu \left( {{{T - W_{0}^{{(0)}}Z} \mathord{\left/ {\vphantom {{T - W_{0}^{{(0)}}Z} {\left( {{{\nu }^{2}} + \omega _{0}^{2}} \right)}}} \right. \kern-0em} {\left( {{{\nu }^{2}} + \omega _{0}^{2}} \right)}}} \right),$ $\nu $ – вещественная постоянная, удовлетворяющая условию $\left| \nu \right| < \left| {{\sigma \mathord{\left/ {\vphantom {\sigma \varepsilon }} \right. \kern-0em} \varepsilon }} \right|.$

Подставив выражение (22) в формулы (20) получим неявное определение переменной $\Omega $ односолитонного решения системы ОРМБ (12)–(15). Это решение является стационарным, и параметр $\nu $ задает длительность солитона. В отличие от системы РМБ, амплитуда солитона не является обратно пропорциональной длительности и неограниченно растет при $\left| \nu \right| \to \left| {{\sigma \mathord{\left/ {\vphantom {\sigma \varepsilon }} \right. \kern-0em} \varepsilon }} \right|.$

Выражение для переменной Ω₀ двухсолитонного решения уравнений МРМБ записывается без потери общности следующим образом:

(23)

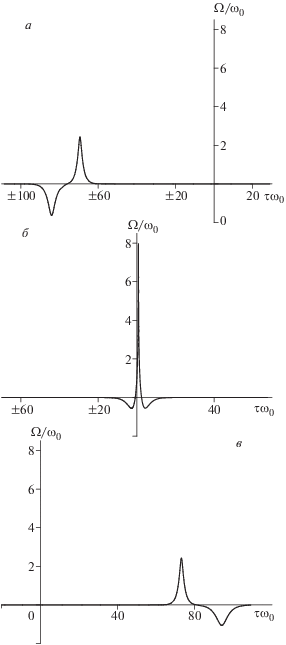
$\begin{gathered} {{\Omega }_{0}} = \frac{1}{\sigma }\frac{\partial }{{\partial T}}\left( {{\text{arctg}}\frac{{{{\nu }_{ + }}\operatorname{sh} {{\theta }_{ - }}}}{{{{\nu }_{ - }}\operatorname{sh} {{\theta }_{ + }}}} + } \right. \\ \left. { + \,\,{\text{arctg}}\frac{{{{\nu }_{ + }}[{{\eta }_{ - }}\operatorname{sh} {{\theta }_{ - }} - 2{{\nu }_{ - }}\varepsilon \sigma \operatorname{ch} {{\theta }_{ - }}]}}{{{{\nu }_{ - }}[{{\eta }_{ + }}\operatorname{sh} {{\theta }_{ + }} - 2{{\nu }_{ + }}\varepsilon \sigma \operatorname{ch} {{\theta }_{ + }}]}}} \right), \\ \end{gathered} $

где ${{\nu }_{ \pm }} = {{({{\nu }_{1}} \pm {{\nu }_{2}})} \mathord{\left/ {\vphantom {{({{\nu }_{1}} \pm {{\nu }_{2}})} 2}} \right. \kern-0em} 2},$ ${{\theta }_{ \pm }} = {{({{\theta }_{1}} \pm {{\theta }_{2}})} \mathord{\left/ {\vphantom {{({{\theta }_{1}} \pm {{\theta }_{2}})} 2}} \right. \kern-0em} 2},$ η_± = σ² ± ± ν₁ν₂ε², ${{\nu }_{1}}$ и ${{\nu }_{2}}$ – вещественные постоянные такие, что $\left| {{{\nu }_{{1,2}}}} \right| < \left| {{\sigma \mathord{\left/ {\vphantom {\sigma \varepsilon }} \right. \kern-0em} \varepsilon }} \right|,$ θ_1,2 = $2{{\nu }_{{1,2}}}\left( {{{T - W_{0}^{{(0)}}Z} \mathord{\left/ {\vphantom {{T - W_{0}^{{(0)}}Z} {\left( {\nu _{{1,2}}^{2} + \omega _{0}^{2}} \right)}}} \right. \kern-0em} {\left( {\nu _{{1,2}}^{2} + \omega _{0}^{2}} \right)}}} \right).$

Подстановка выражения (23) в формулы (20) дает неявное определение переменной $\Omega $ двухсолитонного решения системы ОРМБ (12)–(15). Это решение описывает упругое столкновение стационарных солитонов, рассмотренных выше. Интересные особенности возникают здесь при столкновении солитонов противоположных полярностей $\left( {{{\nu }_{1}}{{\nu }_{2}} > 0} \right).$ Если абсолютная величина одного из параметров ${{\nu }_{1}}$ или ${{\nu }_{2}}$ близка к $\left| {{\sigma \mathord{\left/ {\vphantom {\sigma {\sqrt 2 \varepsilon }}} \right. \kern-0em} {\sqrt 2 \varepsilon }}} \right|,$ то возникает короткоживущий импульс большой амплитуды, динамика которого похожа на динамику волны-убийцы [17] (см. рис. 1). Заметим, что в случае системы РМБ столкновение солитонов противоположных полярностей приводит к возникновению импульса, амплитуда которого равна сумме амплитуд сталкивающихся солитонов.

Рис. 1.

Профили переменной $\Omega $ двухсолитонного решения с параметрами $\beta = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} {8{{\omega }_{0}}}}} \right. \kern-0em} {8{{\omega }_{0}}}},$ $W_{0}^{{(0)}} = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2},$ ${{\nu }_{1}} = 0.65{{\omega }_{0}},$ ${{\nu }_{2}} = 0.5{{\omega }_{0}}$ и $Z = 90{{\omega }_{0}}$ (а), $Z = - 0.95{{\omega }_{0}}$ (б), $Z = - 90{{\omega }_{0}}$ (в).

Выражение для переменной ${{\Omega }_{0}}$ бризерного решения уравнений МРМБ здесь имеет вид

(24)

$\begin{gathered} {{\Omega }_{0}} = \frac{1}{\sigma }\frac{\partial }{{\partial T}}\left( {{\text{arctg}}\frac{{{{\nu }_{R}}\sin {{\theta }_{I}}}}{{{{\nu }_{I}}\operatorname{ch} {{\theta }_{R}}}} + } \right. \\ \left. { + \,\,{\text{arctg}}\frac{{{{\nu }_{R}}[{{{\tilde {\eta }}}_{ - }}\sin {{\theta }_{I}} - 2{{\nu }_{I}}\varepsilon \sigma \cos {{\theta }_{I}}]}}{{{{\nu }_{I}}[{{{\tilde {\eta }}}_{ + }}\operatorname{ch} {{\theta }_{R}} - 2{{\nu }_{R}}\varepsilon \sigma \operatorname{sh} {{\theta }_{R}}]}}} \right), \\ \end{gathered} $

где ${{\tilde {\eta }}_{ \pm }} = {{\sigma }^{2}} \pm \left( {\nu _{R}^{2} + \nu _{I}^{2}} \right){{\varepsilon }^{2}}.$ Подставив выражение (24) в формулы (20) получим неявное определение переменной $\Omega $ бризерного решения системы ОРМБ (12)–(15). Как и в предыдущем случае, здесь могут возникать осцилляции, имеющие заостренную форму, если несущая частота бризера достаточно мала.

${\text{Случай}}\,\,\,\,\beta > 0.$

Здесь выражение для переменной ${{\Omega }_{0}}$ односолитонного решения уравнений МРМБ записывается следующим образом:

(25)

${{\Omega }_{0}} = \frac{1}{\sigma }\frac{\partial }{{\partial T}}{\text{arctg}}\frac{{2{{\sigma }^{2}}\exp (\theta )}}{{{{\sigma }^{2}}[1 - \exp (2\theta )] - {{\nu }^{2}}{{\varepsilon }^{2}}}}.$

Подстановка выражения (25) в формулы (20) дает неявное определение переменной $\Omega $ односолитонного решения системы ОРМБ (12)–(15) в рассматриваемом случае. Это решение стационарное и несингулярное при любом вещественном значении параметра $\nu .$ В пределе $\left| \nu \right| \to \infty $ длительность солитона стремится к наименьшему значению ${{\tau }_{{min}}} = \pi \left| {{\varepsilon \mathord{\left/ {\vphantom {\varepsilon \sigma }} \right. \kern-0em} \sigma }} \right|,$ а амплитуда $\left| \Omega \right|$ стремится к наибольшему значению $\left| {{1 \mathord{\left/ {\vphantom {1 \varepsilon }} \right. \kern-0em} \varepsilon }} \right|.$ Поэтому решение становится “прямоугольным” в этом пределе. Заметим, что подобного рода решения были получены для обобщений уравнения синус-Гордон [10, 11, 16].

Двухсолитонное решение системы ОРМБ (12)–(15) описывает упругое столкновение рассмотренных выше солитонов. При этом столкновение “прямоугольных” солитонов происходит в форме “перетекания” [11].

Выражение для переменной ${{\Omega }_{0}}$ бризерного решения уравнений МРМБ записывается без потери общности в виде

(26)

${{\Omega }_{0}} = \frac{1}{\sigma }\frac{\partial }{{\partial T}}\left( {{\text{arctg}}\frac{{{{\nu }_{R}}{{q}_{ - }}}}{{{{\nu }_{I}}{{p}_{ + }}}} - {\text{arctg}}\frac{{{{\nu }_{R}}{{q}_{ + }}}}{{{{\nu }_{I}}{{p}_{ - }}}}} \right),$

где

$\begin{gathered} {{p}_{ \pm }} = \sigma + i\varepsilon {{\nu }_{I}} \pm i\varepsilon {{\nu }_{R}}\sin ({{\theta }_{I}})\exp ( - {{\theta }_{R}}) + \\ + \,\,(\sigma - i\varepsilon {{\nu }_{I}})\exp ( - 2{{\theta }_{R}}), \\ \end{gathered} $

${{q}_{ \pm }} = {{p}_{ \pm }} - \sigma [1 \mp 2\cos ({{\theta }_{I}})\exp ( - {{\theta }_{R}}) + \exp ( - 2{{\theta }_{R}})].$

Подставив выражение (26) в формулы (20) получим неявное определение переменной $\Omega $ бризерного решения системы ОРМБ (12)–(15).

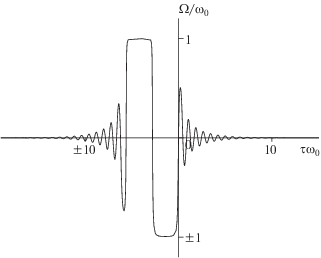
Форма двух осцилляций в центре бризера системы ОРМБ становится “прямоугольной”, если $\left| {{{\nu }_{I}}} \right| > \left| {{\sigma \mathord{\left/ {\vphantom {\sigma \varepsilon }} \right. \kern-0em} \varepsilon }} \right|$ и ${{\nu }_{R}} \to 0.$ Их период и амплитуда примерно равны длительности и амплитуде “прямоугольных” солитонов, т.е. ${{\tau }_{{min}}}$ и $\left| {{1 \mathord{\left/ {\vphantom {1 \varepsilon }} \right. \kern-0em} \varepsilon }} \right|,$ соответственно (см. рис. 2).

Рис. 2.

Профили переменной $\Omega $ бризерного решения с параметрами $\beta = {1 \mathord{\left/ {\vphantom {1 {{{\omega }_{0}}}}} \right. \kern-0em} {{{\omega }_{0}}}},$ $W_{0}^{{(0)}} = {{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2},$ $Z = 0,$ ${{\nu }_{R}} = 0.5{{\omega }_{0}},$ ${{\nu }_{I}} = 8{{\omega }_{0}}.$

ЗАКЛЮЧЕНИЕ

Таким образом, в настоящей работе найдено физическое обобщение системы РМБ при учете переходов на удаленные квантовые состояния с двух выделенных стационарных уровней. Полученная система уравнений ОРМБ (12)–(15) оказалась интегрируемой методом обратной задачи рассеяния. Важно, что с помощью системы ОРМБ можно рассматривать ситуации, при которых не справедливо приближение внезапных возбуждений, предполагающее выполнение условия (1). Это расширяет спектральный диапазон ПКИ, динамика которых описываются с помощью системы ОРМБ.

Исследованные здесь солитонные и бризерные решения обладают особенностями, отличающими их от соответствующих решений системы РМБ. В значительной степени это касается процесса столкновения солитонов различных полярностей. В отличие от столкновения солитонов системы РМБ здесь может возникать короткоживущий импульс большой амплитуды, динамика которого схожа с динамикой волны-убийцы.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 19-02-00234а).

Список литературы

Brabec T., Krausz F. // Rev. Mod. Phys. 2000. V. 72. P. 545.
Маймистов А.И. // Квант. электрон. 2000. Т. 30. С. 287; Maimistov A.I. // Quant. Electron. 2000. V. 30. P. 287.
Leblond H., Mihalache D. // Phys. Rep. 2013. V. 523. P. 61.
Eilbeck J.C., Gibbon J.D., Caudrey P.J., Bullough R.K. // J. Phys. A. 1973. V. 6. P. 1337.
Захаров В.Е., Манаков С.В., Новиков С.П., Питаевский Л.П. Теория солитонов: Метод обратной задачи. М.: Наука, 1980.
Додд Р., Эйлбек Дж., Гиббон Дж., Моррис Х. Солитоны и нелинейные волновые уравнения. М.: Мир, 1988.
Фаддеев Л.Д. // УФН. 2013. Т. 183. С. 487; Faddeev L.D. // Phys. Usp. 2013. V. 56. P. 465.
Беленов Э.М., Назаркин А.В. // Письма в ЖЭТФ. 1990. Т. 51. С. 252; Belenov E.M., Nazarkin A.V. // JETP Lett. 1990. V. 51. P. 288.
Беленов Э.М., Назаркин А.В., Ущаповский В.А. // ЖЭТФ. 1991. Т. 100. С. 762; Belenov E.M., Nazar-kin A.V., Ushchapovskii V.A. // Sov. Phys. JETP. 1991. V. 73. P. 422.
Сазонов С.В. // ЖЭТФ. 2014. Т. 146. С. 483; Sazonov S.V. // JETP. 2014. V. 119. P. 423.
Sazonov S.V., Ustinov N.V. // Phys. Rev. A. 2018. V. 98. Art. № 063803.
Zabolotskii A.A. // Phys. D. 2003. V. 185. P. 117.
Bakhar N.V., Ustinov N.V. // Proc. SPIE. 2006. V. 6181. Art. № 61810Q.
Сазонов С.В., Устинов Н.В. // ТМФ. 2007. Т. 151. № 2. С. 228; Sazonov S.V., Ustinov N.V. // Theor. Math. Phys. 2007. V. 151. P. 632.
Сазонов С.В., Устинов Н.В. // ФТТ. 2008. Т. 50. № 6. С. 1076; Sazonov S.V., Ustinov N.V. // Phys. Solid State. 2008. V. 50. P. 1122.
Ustinov N.V. // J. Math. Phys. 2019. V. 60. Art. № 013503.
Dudley J.M., Dias F., Erkintalo M. et al. // Nat. Photon. 2014. V. 8. P. 755.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал