1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 84, № 1, 2020

Известия РАН. Серия физическая, 2020, T. 84, № 1, стр. 87-89

Обобщенная синхронизация в однонаправлено связанных системах с запаздыванием

А. Д. Плотникова 1, *, О. И. Москаленко 1

1 Федеральное государственное бюджетное образовательное учреждение высшего образования “Саратовский национальный исследовательский государственный университет имени Н.Г. Чернышевского”
Саратов, Россия

* E-mail: adkoloskova@gmail.com

Поступила в редакцию 29.07.2019
После доработки 30.08.2019
Принята к публикации 27.09.2019

Полный текст (PDF)

Аннотация

Проведено исследование обобщенной синхронизации в системах с запаздыванием на примере двух связанных радиотехнических генераторов и уравнений Маккея–Гласса. Получена зависимость порогового значения силы связи, соответствующего установлению синхронизации, от времени запаздывания при различных комбинациях управляющих параметров. Установлена общая закономерность в виде увеличения и последующего насыщения порогового значения параметра связи с изменением времени запаздывания.

Одним из наиболее интересных типов хаотической синхронизации является обобщенная синхронизация [1]. Это явление может возникать между различными по своей природе осцилляторами, в том числе с разной размерностью фазового пространства. Индикатором установления обобщенной синхронизации является наличие функциональной зависимости (функционала) между состояниями взаимодействующих систем.

Использование данного режима актуально в системах с запаздыванием в сфере скрытой передачи информации и радиофизики [2–7]. Связано это с отличительной особенностью систем с отклоняющимся аргументом – бесконечномерным фазовым пространством, а следовательно, и неиссякаемым количеством показателей Ляпунова. В первой упомянутой области описанное свойство способно обеспечить необходимую степень конфиденциальности при передаче информации, а во втором примере это позволит сгенерировать различные режимы, в том числе гиперхаос высокой размерности.

В настоящей работе проведены исследования особенностей режима обобщенной синхронизации в таких системах. В качестве исследуемых систем были выбраны две модели однонаправленно связанных систем, широко распространенные в радиофизике, а также применяемые в сфере скрытой передачи информации. Первая из них представляет собой два связанных уравнения Маккея–Гласса [8, 9] с диссипативным слагаемым:

(1)
$\begin{gathered} {{{\dot {x}}}_{1}}\left( t \right) = f\left( {{{x}_{1}}\left( {t - {\tau }} \right)} \right) - {{k}_{1}}{{x}_{1}}\left( t \right), \\ {{{\dot {x}}}_{2}}\left( t \right) = f\left( {{{x}_{2}}\left( {t - {\tau }} \right)} \right) - {{k}_{2}}{{x}_{2}}\left( t \right) + \\ + \,\,{{k}_{3}}\left( {{{x}_{1}}\left( t \right) - {{x}_{2}}\left( t \right)} \right), \\ \end{gathered} $
где

(2)
$f\left( {x\left( {t - {\tau }} \right)} \right) = {{ax\left( {t - {\tau }} \right)} \mathord{\left/ {\vphantom {{ax\left( {t - {\tau }} \right)} {\left( {1 + {{{\left( {x\left( {t - {\tau }} \right)} \right)}}^{b}}} \right)}}} \right. \kern-0em} {\left( {1 + {{{\left( {x\left( {t - {\tau }} \right)} \right)}}^{b}}} \right)}}.$

Изначально уравнение Маккея–Гласса было предложено в качестве модели выработки красных кровяных клеток для пациентов с лейкемией. Позже эта модель стала популярной в теории хаоса как система с большим количеством положительных показателей Ляпунова, которое, к тому же, можно варьировать. Электронный аналог этой системы был предложен в работе [10].

Второй пример основан на радиотехнических генераторах с запаздыванием, предложенных в работе [11]:

(3)
$\begin{gathered} {{{\dot {x}}}_{1}}\left( t \right) = - {{x}_{1}}\left( t \right) + {{k}_{1}}f\left( {{{x}_{1}}\left( {t - \tau } \right)} \right), \\ {{{\dot {x}}}_{2}}\left( t \right) = - {{x}_{2}}\left( t \right) + {{k}_{2}}f\left( {{{x}_{2}}\left( {t - \tau } \right)} \right) + \\ + \,\,{{k}_{3}}\left( {f\left( {{{x}_{1}}\left( {t - \tau } \right)} \right) - f\left( {{{x}_{2}}\left( {t - \tau } \right)} \right)} \right), \\ \end{gathered} $
где f(x) представляет собой нелинейную функцию вида:

(4)
$f\left( x \right) = a - {{x}^{2}},$

${{x}_{1}}\left( t \right)$ и ${{x}_{2}}\left( t \right)$ – переменные, характеризующие поведение ведущей и ведомой систем, соответственно, k1 и k2 – параметры, относящиеся к первому и второму генераторам, ${{k}_{3}}$ – параметр связи, f(x) – нелинейная функция, a – управляющий параметр, τ – время запаздывания.

Для детектирования обобщенной синхронизации в системах с запаздыванием использовалось вычисление спектра показателей Ляпунова по методике, разработанной именно для такого класса уравнений [12]. Порогом установления режима служил момент перехода старшего условного показателя Ляпунова в область отрицательных значений [13]. Для уточнения результатов был использован метод вспомогательной системы [14], согласно которому, если между идентичными по управляющим параметрам ведомой и вспомогательной системами (но с разными начальными условиями) устанавливается эквивалентность состояний, то в паре ведущей–ведомой систем наступает обобщенная синхронизация.

В рамках данной работы также исследован вопрос о том, как увеличение времени запаздывания изменяет порог режима обобщенной синхронизации. В работе [15] подобное исследование проводилось для режима полной синхронизации, а в качестве модели выступали связанные идентичные уравнения Маккея–Гласса. Не составляет труда провести подобные вычисления для той же модели (1), но находящейся в режиме обобщенной синхронизации. В данном случае, как отмечалось выше, установление синхронного режима возможно как в идентичных, так и в разных по управляющим параметрам системах, поэтому в данной работе рассмотрен также вопрос о влиянии вариации управляющих параметров, указывающих на количество положительных показателей Ляпунова в “автономных” системах, на порог установления синхронного режима.

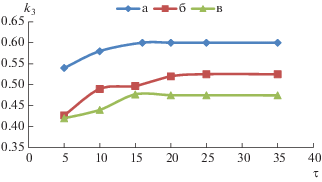
На рис. 1 приведены графики зависимости времени запаздывания от параметра связи τ(k3) для следующих комбинаций управляющих параметров: а) ${{k}_{1}}$ = 1.27, ${{k}_{2}}$ = 1.23 (по пять положительных показателей Ляпунова у ведущей и ведомой автономных систем); б) ${{k}_{1}}$ = 1.345, ${{k}_{2}}$ = 1.34 (по четыре положительных показателя в каждой системе); в) ${{k}_{1}}$ = 1.27, ${{k}_{2}}$ = 1.345 (у ведущей пять, у ведомой четыре положительных показателя). Сравнивая зависимости между собой можно сделать вывод о том, что пороговое значение параметра связи вначале увеличивается с ростом времени запаздывания, а затем достигает насыщения. Важно отметить, что для каждой комбинации параметров этот уровень насыщения отличается по величине. Также стоит отметить увеличение количества положительных показателей Ляпунова с изменением τ [15].

Рис. 1.

Зависимость параметра связи ${{k}_{3}}$ от времени запаздывания τ для однонаправленно связанных уравнений Маккея–Гласса (1).

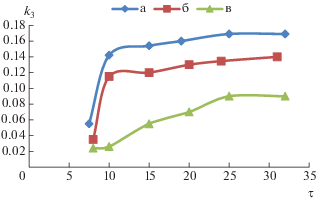
Аналогичные результаты были получены для генераторов с запаздыванием (3) с различными значениями параметров $~{{k}_{1}}$ и ${{k}_{2}}$. Эти результаты представлены на рис. 2: а) при${\text{\;}}{{k}_{1}}$ = 1.015, ${{k}_{2}}$ = 1.018 (по два положительных показателя Ляпунова); б) при ${\text{\;}}{{k}_{1}}$ = 1.013, ${\text{\;}}{{k}_{2}}$ = 1.005 (у ведущей два, у ведомой один положительный показатель); в) при ${{k}_{1}}$ = = 0.996, ${\text{\;}}{{k}_{2}}$ = 0.988 (по одному положительному показателю). Из сравнения рис. 1 и 2 видно, что полученные зависимости схожи с предыдущим случаем, разница состоит лишь в мéньших значениях параметра связи, соответствующего насыщению, что обусловлено как свойствами самих систем, так и меньшим числом положительных показателей Ляпунова в автономном случае.

Рис. 2.

Зависимость параметра связи ${{k}_{3}}$ от времени запаздывания τ для однонаправленно связанных радиофизических генератора (3).

Таким образом, в данной работе было проведено исследование обобщенной синхронизации в однонаправлено связанных системах с запаздыванием. Было изучено, как меняется пороговое значение силы связи в зависимости от различных комбинаций управляющих параметров, а также при изменении времени запаздывания. Установлено, что во всех рассмотренных случаях порог обобщенной синхронизации выходит на уровень насыщения, величина которого существенным образом зависит от числа положительных показателей Ляпунова, реализуемых во взаимодействующих системах в автономном случае.

Работа выполнена при частичной финансовой поддержке Совета по грантам Президента РФ для государственной поддержки молодых российских ученых (проект № МК-531.2018.2).

Список литературы

  1. Rulkov N.F., Sushchik M.M., Tsimring L.S. et al. // Phys. Rev. E. 1995. V. 51. P. 980.

  2. Короновский А.А., Москаленко О.И., Храмов А.Е. // УФН. 2009. Т. 179. № 12. С. 1281; Koronovskii A.A., Moskalenko O.I., Hramov A.E. // Phys. Usp. 2009. V. 52. № 12. P. 1213.

  3. Mensour B., Longtin A. // Phys. Lett. A. 1998. V. 244. P. 59.

  4. Короновский А.А., Москаленко О.И., Попов П.В., Храмов А.Е. // Изв. РАН. Сер. физ. 2008. Т. 72. № 1. С. 143; Koronovskii A.A., Moskalenko O.I., Hramov A.E. // Bull. Russ. Acad. Sci. Phys. 2008. V. 72. № 1. P. 131.

  5. Стародубов А.В., Короновский А.А., Храмов А.Е. и др. // Изв. РАН. Сер. физ. 2008. Т. 72. № 1. С. 148; Starodubov A.V., Koronovskii A.A., Hramov A.E., et al. // Bull. Russ. Acad. Sci. Phys. 2008. V. 72. № 1. P. 136.

  6. Dmitriev B.S., Hramov A.E., Koronovskii A.A. et al. // Phys. Rev. Lett. 2009. V. 02. Art. № 074101.

  7. Starodubov A.V., Koronovskii A.A., Hramov A.E. et al. // Phys. Wave Phenom. 2010. V. 18. № 1. P. 51.

  8. Mackey M.C., Glass L. // Science. 1977. V. 197. P. 287.

  9. Пономаренко В.И., Прохоров М.Д. // Радиотехн. и электрон. 2004. Т. 49. № 9. С. 1098; Ponomarenko V.I., Prokhorov M.D. // J. Commun. Techn. Electronics. 2004. V. 49. № 9. P. 1031.

  10. Kittel A., Parisi J., Pyragas K. // Physica D. 1998. V. 112. № 4. P. 459.

  11. Ponomarenko V.I., Prokhorov M.D. // Phys. Rev. E. 2002. V. 66. Art. № 026215.

  12. Колоскова А.Д., Москаленко О.И., Короновский А.А. // Письма в ЖТФ. 2018. Т. 44. № 9. С. 19; Koloskova A.D., Moskalenko O.I., Koronovskii A.A. // Tech. Phys. Lett. 2018. V. 44. № 5. P. 374.

  13. Pyragas K. // Phys. Rev. E. 1997. V. 56. № 5. P. 5183.

  14. Abarbanel H.D.I., Rulkov N.F., Sushchik M. // Phys. Rev. E. 1996. V. 53. № 5. P. 4528.

  15. Pyragas K. // Phys. Rev. E. 1998. V. 58. № 3. P. 3067.

  16. Farmer J.D. // Phys. D. 1982. P. 366.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал