Известия РАН. Серия физическая, 2020, T. 84, № 11, стр. 1674-1676
Расшифровка диэлектрических спектров: Коула–Коула, элемент постоянной фазы, логнормальное распределение
А. С. Богатин 1, *, А. Л. Буланова 1, Е. В. Андреев 1, С. А. Ковригина 1, И. О. Носачев 1
1 Федеральное государственное автономное образовательное учреждение высшего образования
“Южный федеральный университет”, Научно-исследовательский институт физики
Ростов-на-Дону, Россия
* E-mail: asbbogatin@sfedu.ru
Поступила в редакцию 18.06.2020
После доработки 10.07.2020
Принята к публикации 27.07.2020
Аннотация
Обсуждаются способы описания диэлектрических спектров с использованием распределения Коула–Коула, ячейки постоянной фазы, логнормального распределения. Во всех этих случаях центральные части частотных зависимостей действительных частей комплексной диэлектрической проницаемости хорошо описывают эксперимент. Значительные расхождения с экспериментом имеют место для высокочастотных частей частотных зависимостей действительных частей комплексной электропроводности при использовании распределения Коула–Коула. Логнормальное распределения позволяет связать ширину паспределения с физческим смыслом развивающихся процессов релаксационных поляризаций.
При исследовании симметрийных диэлектрических спектров чаще всего приходится сталкиваться со спектрами, которые могут описываться распределением Коула–Коула [1]. Формула для комплексной диэлектрической проницаемости в этом распределении релаксаторов была подобрана эмпирически:
(1)
$\varepsilon {\kern 1pt} ' = {{\varepsilon }_{\infty }} + \frac{{\vartriangle \varepsilon }}{{1 + {{{\left( {i\omega \tau } \right)}}^{{1 - {\alpha }}}}}},$здесь i – мнимая единица, △ε = εst – ε∞ вклад релаксационного процесса в диэлектрическую проницаемость вещества, εst – статическая диэлектрическая проницаемость, ε∞ – высокочастотная диэлектрическая проницаемость, ω – круговая частота электрического поля, α – параметр распределения, τ – время релаксации процесса. Подбирая Δε, τ, α можно для широкого круга экспериментально наблюдаемых спектров получить хорошее соответствие между экспериментом и теоретическим описанием для частотной зависимости действительной части диэлектрической проницаемости ε'. Как правило, для частотной зависимости мнимой части диэлектрической проницаемости такое соответствие наблюдается только в цетральной частотной части спектра. В высокочастотной части часотной зависимости действительной части комплексной электропроводности σ' при использовании распределения Коула–Коула наблюдается увеличение σ' при увеличении частоты ω (рис. 1). В экспериментальных спектрах такое увеличение не наблюдается, если в веществе отсутствует второй релаксационный процесс. С физической точки зрения увеличение σ' так же не должно иметь место, поскольку физический смысл σ' – удельная электропроводность диэлектрических потерь [2]. За пределами частотной области релаксационного процесса удельная электропроводность диэлектрических потерь не должна зависеть от частоты.
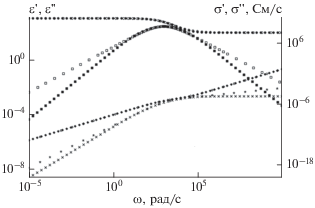
Рис. 1.
Расчетные частотные зависимости ε', ε", σ', σ" при использовании распределения Коула–Коула и логнормального распределения релаксаторов. Распределение Коула–Коула (α = 0.34) ⚫ – ε'; ◻ – ε"; × – σ'; ◆ – σ". Логнормальное распределение (b = 0.4) ⚪ – ε'; ◻ – ε"; ☆ – σ'; ◇ – σ".
Частотный рост σ' при импедансном описании диэлектрических спектров, не опиывается описывать с использованием распределения Коула–Коула. Эквивалентная электрическая схема для этого случая имеет вид, изображенный на рис. 2. Это линейный резистор, включенный последовательно с ячейкой постоянной фазы [3]. Импеданс ячейки постоянной фазы (CPE) имеет вид:
где A – коэффициент пропорциональности; n – экспоненциальный показатель. Импеданс всей эквивалентной схемы описывается соотношением:Рис. 2.
Эквивалентная электрическая схема образца диэлектрика, описываемого с помощью ячейки постоянной фазы.

Действительная и мнимая части комплексной электропроводности эквивалентной схемы описываются соотношениями:
(4)
$\sigma _{{Total\left( {CPE} \right)}}^{'} = \frac{{A{{\omega }^{n}}\left( {RA{{\omega }^{n}} + \cos \left( {\frac{{n\pi }}{2}} \right)} \right)}}{{{{{\left( {RA{{\omega }^{n}}} \right)}}^{2}} + 2RA{{\omega }^{n}}\cos \left( {\frac{{n\pi }}{2}} \right) + 1}},$(5)
$~\sigma _{{Total\left( {CPE} \right)}}^{'} = \frac{{A{{\omega }^{n}}\sin \left( {\frac{{n\pi }}{2}} \right)}}{{{{{\left( {RA{{\omega }^{n}}} \right)}}^{2}} + 2RA{{\omega }^{n}}\cos \left( {\frac{{n\pi }}{2}} \right) + 1}}.$Частотные зависимости этих величин приведены на рис. 3. В частотных зависимостях σ' выше области релаксации наблюдается плато.
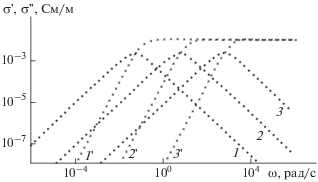
Рис. 3.
Расчетные частотные зависимости действительной σ' и мнимой σ" частей комплексной электропроводности при использовании ячейки постоянной фазы. × – σ'; ◆ – σ". N = 1; R = 100 Ом; A = 10–1 (1, 1 '); 10–3 (2, 2 '); 10–4 (3, 3 ').
Плотность вероятности времен релаксации при распределении Коула–Коула описывается соотношением [4]:
(6)
$F\left( s \right)ds = \frac{1}{{2\pi }}\frac{{{\text{sin}}\alpha \pi }}{{ch\left( {1 - \alpha } \right)s - {\text{cos}}\alpha \pi }}ds,$Перейти от функции вероятности распределения к частотной зависимости комплексной диэлектрической проницаемости можно следующим образом:
(8)
$\frac{{\varepsilon {\kern 1pt} * - \,\,{{\varepsilon }_{\infty }}}}{{{{\varepsilon }_{{st}}} - {{\varepsilon }_{\infty }}}} = \int\limits_0^\infty {\frac{{G\left( \tau \right)d\tau }}{{1 + j\omega \tau }}} .$Если подстановка (6) в (8) дает интеграл, приводящий к (1), то при подстановке (7) взять интеграл в конечном виде не удается. Нахождение ε*(ω) в этом случае возможно только путем численного интегрирования. Наиболее простой путь для логнормального распределения аппроксимация G(S) рядом Тейлора. В результате численного интегрирования удается рассчитывать частотные зависимости ε', ε", σ', σ" и сопоставлять их с экспериментальными зависимостями. Расчетные зависимости этих величин приведены на рис. 1. В центральных частотных частях зависимостей ε'(ω) и ε"(ω) наблюдается хорошее соответствие между результатами расчетов при использовании распределения Коула–Коула и логнормального распределения. В высокочастототной области зависимостей σ'(ω) для логнормального распределения наблюдается плато, как в экспериментальных спектрах, так и в расчетных спектрах, полученных методом импедансной спектроскопии с использованием ячейки постоянной фазы. Таким образом, логнормальное распределение адекватнее описывает экспериментальные диэлектрические спектры, чем распределение Коула–Коула. Кроме того использование логнормального распределения позволяет при определении ширины распределения b более четким образом выявлять физический смысл рассматриевамого релаксационного процесса. Установление взаимосвязи между параметрами всех трех рассмотренных теоретических описаний экспериментальных диэлектрических спектров позволяет описать переход к сильным релаксационным процессам [5, 6].
Список литературы
Cole R.H., Cole R.H. // J. Chem. Phys. 1941. V. 9. P. 341.
Сканави Г.И. Физика диэлектриков. М.–Л.: ГИТТЛ, 1949.
Macdonald I.R. Impedance spectroscopy. N.Y.: Wiley, 2005.
Челидзе Т.Л., Деревянко А.И., Куркленко О.Д. Электрическая спектроскопия гетерогенных систем. Киев: Наукова думка, 1977. 232 с.
Богатин А.С., Андреев Е.В., Ковригина С.А., Богатина В.Н. // Изв. РАН. Сер. физ. 2014. Т. 78. № 4. С. 483; Bogatin A.S., Andreev E.V., Kovrigina S.A., Bogatina V.N. // Bull. Russ. Acad. Sci. Phys. 2014. V. 78. № 4. P. 317.
Богатин А.С., Турик А.В., Ковригина С.А., Андреев Е.В. // Изв. РАН. Сер. физ. 2010. Т. 74. № 9. С. 1266; Bogatin A.S., Andreev E.V., Kovrigina S.A., Bogatina V.N. // Bull. Russ. Acad. Sci. Phys. 2010. V. 74. № 9. P. 1212.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая


