1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 84, № 11, 2020

Известия РАН. Серия физическая, 2020, T. 84, № 11, стр. 1638-1642

Исследование влияния броуновского движения на мёссбауэровские спектры наночастиц в среде, моделирующей клеточную цитоплазму

А. Ю. Юреня 1, 2, *, А. А. Никитин 2, 3, Р. Р. Габбасов 1, М. А. Поликарпов 1, В. М. Черепанов 1, М. А. Чуев 4, М. А. Абакумов 3, В. Я. Панченко 1, 2

1 Федеральное государственное бюджетное учреждение “Национальный исследовательский центр “Курчатовский институт”
Москва, Россия

2 Федеральное государственное бюджетное образовательное учреждение высшего образования “Московский государственный университет имени М.В. Ломоносова”
Москва, Россия

3 Национальный исследовательский технологический университет “МИСиС”
Москва, Россия

4 Федеральное государственное бюджетное учреждение науки Физико-технологический институт имени К.А. Валиева Российской академии наук
Москва, Россия

* E-mail: antonyurenya@gmail.com

Поступила в редакцию 18.06.2020
После доработки 10.07.2020
Принята к публикации 27.07.2020

Полный текст (PDF)

Аннотация

Нестандартный характер внутриклеточного движения связан со значительным содержанием макромолекул и во многом определяется явлением аномальной диффузии. С помощью мёссбауэровской спектроскопии впервые в наносекундном временном масштабе исследованы особенности движения наночастиц в концентрированных растворах белка, моделирующих цитоплазму. Проведен сравнительный анализ нано-вязкости и макро-вязкости сред.

ВВЕДЕНИЕ

Процессы внутриклеточного транспорта относятся к одной из наименее изученных областей биологии клетки [1]. Еще более 100 лет назад в работах Эйнштейна и Смолуховского было показано, что транспорт мельчайших частиц в простых растворах описывается законами броуновского движения [2, 3]. Тем не менее, даже в рамках современной теории оказывается невозможным описание процессов движения макромолекул и частиц в биологических средах [4, 5]. В живой клетке содержится множество макромолекул, таких как белки, нуклеиновые кислоты и сложные сахара, объемная доля которых достигает 40% от общего объема жидкой фазы клеточной цитоплазмы. Одновременное присутствие таких молекул в среде приводит к эффекту заполненного объема, т.н. “макромолекулярному краудингу” (ММК) [6]. Краудинг оказывает влияние на транспортные процессы [4], термодинамические параметры, скорость и равновесие биохимических реакций [7–10]. Специфику движения в клетках в первую очередь связывают с явлением аномальной диффузии [7, 11]. Существует несколько упрощенных моделей, описывающих нестандартное движение макромолекул в условиях диффузии ММК [9, 11], однако понимание динамики этого движения до сих пор остается одной из ключевых задач биологии [8, 13].

При исследовании движения в условиях аномальной диффузии ММК в противовес макроскопической вязкости среды часто рассматривают понятие микро- и нано-вязкости [7, 13]. Выделение микро- и нано-вязкости связано с тем, что в условиях ММК движение броуновской частицы характеризуется коэффициентом диффузии, величина которого зависит от временного и пространственного масштаба измерений. В таких экспериментах исследуется среднеквадратичное смещение броуновской частицы за фиксированные интервалы времени. Современные подходы основаны на оптическом наблюдении “броуновской частицы”, в качестве которой используются флуоресцентно-меченые белки или наноразмерные частицы-зонды [7, 15–17]. Основные усилия исследователей сфокусированы на усовершенствовании экспериментальной модели с целью уменьшения масштаба измерений. Тем не менее, наблюдение индивидуального движения наноразмерных объектов оптическими методами имеет ряд ограничений, прежде всего обусловленных дифракционным пределом, что, в действительности, не позволяет получать высокоточных данных о движении частиц ни в нанометровом, ни в наносекундном диапазоне. Наиболее актуальные результаты были получены с пространственным и временным разрешением >100 нм и >1 мкс соответственно [7, 17].

Ранее нами был предложен новый подход к изучению динамики броуновских частиц в условиях ММК [18, 19 ]. В основе подхода лежит мёссбауэровская спектроскопия диспергированных в исследуемой среде наночастиц (НЧ), изготовленных на основе изотопа 57Fe. Измерение мёссбауэровских спектров ансамбля НЧ в составе вязких сред обнаруживает уширение линии вследствие их броуновского движения [20]. В первом приближении диффузионную трансформацию спектра частиц можно рассматривать как однородное уширение ∆Γ всех спектральных линий [21, 22], которое описывается формулой:

(1)
$\Delta \Gamma = \frac{{E_{0}^{2}}}{{3\hbar \pi {{c}^{2}}}}\frac{T}{{R\eta }},$
где T – температура, η – коэффициент динамической вязкости, R – размер частицы, $E_{0}^{2}$ – энергия гамма-кванта.

В соответствии с формулой (1) уширение спектра НЧ в вязкой среде относительно спектра порошкового образца обратно пропорционально ее вязкости. Таким образом, значение вязкости среды может быть получено из совместного анализа спектра НЧ, диспергированных в исследуемой среде, и порошкового спектра НЧ, измеренного при той же температуре. Существенно, что временное разрешение предлагаемого подхода определяется временем жизни возбужденного состояния ядра 57Fe (<10–7 с). При этом усредненные параметры движения частиц за указанное время непосредственно отражены в характеристиках получаемых спектров, что фактически исключает пространственное ограничение измерений. Таким образом, масштаб измерения на два порядка превосходит нижнюю границу имеющихся оптических методов, и вычисляемая по формуле (1) величина вязкости соответствует понятию нано-вязкости. В предшествующих работах нами была разработана методика анализа сверхтонкой структуры мёссбауэровских спектров, учитывающая разделение вкладов магнитной релаксации и броуновского движения НЧ в жидких средах [19]. Методика была успешно апробирована в исследовании параметров движения наночастиц-зондов, диспергированных в простых растворах с известной вязкостью [19, 23].

В основе данной работы лежит исследование броуновского движения НЧ в условиях ММК с помощью мёссбауэровской спектроскопии. При исследовании систем, моделирующих ММК, основными параметрами являются динамическая вязкость среды η и объемная доля макромолекул φ в этой среде [11]. Для исследования было получено три образца вязких сред, содержащих диспергированные НЧ феррита кобальта Co57Fe2O4. Модельные среды изготавливались на основе воды, глицерина и бычьего сывороточного альбумина (БСА), используемого в качестве краудинг-агента, объемная доля которого в среде составляла: 0.5 и 10%. Соотношение компонентов в каждом образце было подобрано таким образом, чтобы их макроскопическая вязкость была равна и составляла η0 = 50 сП. Жидкие среды с вязкостью такого порядка присутствуют в компартментах живых клеток [24] и могут исследоваться с применением НЧ на стандартном мёссбауэровском спектрометре [19]. По результатам измерения и анализа спектров образцов НЧ, диспергированных в модельных средах с различным содержанием краудинг-агента, было установлено соотношение нано-вязкости сред η, определяемой из формулы (1), и макроскопической вязкости η0, измеряемой экспериментально при помощи вискозиметра.

ЭКСПЕРИМЕНТ

Синтез НЧ Co57Fe2O4

Синтез НЧ осуществлялся методом высокотемпературного соосаждения. Для этого 0.519 г 57FeCl3 (содержание изотопа 57Fe ≥ 95%), было растворено в 6.4 мл деионизированной воды, после чего к раствору было добавлено 0.689 г CoCl2 · 6H2O, растворенного в 0.8 мл деионизированной воды и 0.2 мл HCl (36%). Полученный раствор добавляли по каплям к 32 мл 1 М раствора NaOH, предварительно нагретого до температуры кипения. Кипение раствора поддерживали в течение 30 мин при непрерывном перемешивании. По окончании реакции смесь охлаждали до комнатной температуры, НЧ отделяли от раствора центрифугированием и трижды промывали деионизированной водой. Полученные НЧ феррита кобальта были дополнительно стабилизированы в воде путем модификации их поверхности цитрат-ионами [25].

Получение модельных сред

Заданную объемную долю краудинг-агента φ при получении модельных сред на основе БСА, моделирующих ММК, рассчитывали с помощью формулы [11]:

(2)
${\varphi } = \frac{{\vartheta {{m}_{{BSA}}}}}{{{{V}_{{solv}}} + \vartheta {{m}_{{BSA}}}}},$
где Vsolv – объем растворителя, в котором растворяется БСА с массой mBSA, ϑ – специфический объем БСА в растворителе. Значение ν для БСА в водных растворах глицерина составляет порядка 0.69 мл/г [26]. Поскольку чистые водные растворы БСА с заданным φ имеют определенные значения вязкости, при конкретной температуре, с целью получения модельных растворов с φБСА = 5 и 10% и заданной вязкостью чистый белок растворяли в водных растворах глицерина. Необходимое соотношение глицерина и воды в модельных средах было определено в калибровочных экспериментах с применением ротационного вискозиметра RV-2T (W&J Instrument Co., LTD). Измеренная вязкость исследуемых образцов η0 составила 50 ± 2 сП при температуре T = 276.0 К, соответствующей температуре измерения спектров.

Получение модельных сред с диспергированными НЧ

Для получения сред с НЧ, в процессе изготовления в качестве водной компоненты раствора использовали коллоидный раствор НЧ в аналогичной пропорции. Итоговая концентрация НЧ, диспергированных в средах, составляла 1 мг · мл–1. Измерения макроскопической вязкости полученных сред с диспергированными НЧ показали, что данная концентрация НЧ не оказывает влияния на величину вязкости сред. Полученные среды обрабатывались в ультразвуковой бане, после чего переливались в плоские цилиндрические кюветы из плексигласа 1 мл для последующих измерений.

Анализ формы и размеров НЧ

Морфологию и размер “ядра” НЧ устанавливали с использованием метода просвечивающей электронной микроскопии. Исследования проводили на микроскопе JEOL JEM-1400. Средний размер НЧ вычисляли с использованием программного обеспечения ImageJ. НЧ в исходном коллоиде и образцах сред анализировали на монодисперсность методом динамического светорассеяния с использованием прибора Malvern Zetasizer Nano ZS.

Мёссбауэровская спектроскопия

Спектры образцов измеряли при Т = 276.0 ± ± 0.1 К на спектрометре MС-1104Em с использованием штатного проточного криостата. Диапазон скоростей источника гамма-квантов при исследовании образцов с модельными средами составил ±48 мм/с, что в 4 раза больше диапазона ±12 мм/с при измерении спектра высушенных НЧ. Для калибровки спектрометра на другом канале регистрации измеряли эталонный поглотитель α-Fe. В качестве источника гамма-квантов использовали 57Co(Rh) активностью 10 мКи. Изомерные сдвиги определяли относительно линии поглощения α-Fe.

РЕЗУЛЬТАТЫ

Установленный по микрофотографиям средний диаметр НЧ составил 9 ± 2 нм. Исследование гидродинамических параметров НЧ показало длительное (7 сут) сохранение монодисперсности НЧ как в исходном водном растворе, так и в водно-глицериновых растворах БСА. Сама по себе молекула БСА представляет собой глобулу в форме сплюснутого эллипсоида вращения с полуосями 1.8 на 4.6 нм [11]. Таким образом, синтезированные НЧ соразмерны краудинг-агенту.

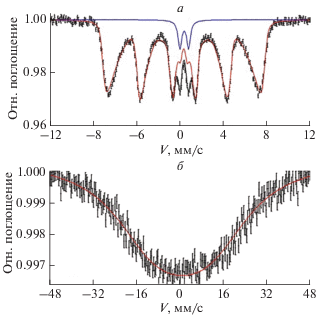
Анализ сверхтонкой структуры мёссбауэровских спектров проводили в рамках многоуровневой модели релаксации ферримагнитных наночастиц [27]. Разделение вкладов магнитной релаксации и броуновского движения НЧ в среде проводили на основе методики, описанной в [19]. На рис. 1а представлен спектр порошкового образца наночастиц феррита кобальта и спектр этих же частиц, диспергированных в растворе с φБСА = 10%. Наблюдается значительное видоизменение спектра НЧ в вязкой среде, которое обусловлено их броуновским движением. Характерный секстет линий трансформировался в уширенный синглет: на рис. 1б спектр НЧ в растворе БСА приведен на четырехкратно увеличенном масштабе скоростей. Броуновское уширение спектральных линий сопровождается значительным снижением вероятности резонансного поглощения в образце: максимумы относительного поглощения НЧ в среде на порядок меньше. Аналогичная трансформация спектров наблюдается для всех образцов вязких сред с НЧ. По результатам обработки уширение спектральных линий составило ∆Γ0 = 45 ± 6 мм/c, ∆Γ5 = 33 ± 6 мм/c, ∆Γ10 = 29 ± ± 4 мм/c для образцов с φБСА 0.5 и 10% соответственно. Данный результат говорит о том, что, несмотря на равную вязкость растворов η0 = 50 сП, характер броуновского движения НЧ в них различен. Поскольку уширение спектральных линий менее выражено для образцов, содержащих БСА, можно заключить, что в условиях ММК средняя скорость движения НЧ оказывается ниже, чем в простом растворе. При этом средняя скорость движения НЧ снижается с повышением концентрации БСА в растворе.

Рис. 1.

57Fe-мёссбауэровские спектры НЧ феррита кобальта Co57Fe2O4. Представлен спектр порошкового образца НЧ (а) и спектр НЧ, диспергированных в водно-глицериновом растворе БСА с объемной долей φБСА = 10% (б). Диффузионное уширение спектра НЧ в среде составляет ∆Γ10 = 29 ± 4 мм/c. Спектры измерены при температуре T = 276.0 ± 0.1 К.

Согласно уравнению (1), уширение спектра НЧ является функцией нано-вязкости раствора η, в соответствии с которой происходит их броуновское движение за характерное время t ∼ 10–7 с. В условиях водного раствора глицерина броуновское движение НЧ происходит в отсутствие ММК, поэтому нано-вязкость может рассматриваться как независящая от масштаба измерения величина, соответствующая значению макроскопической вязкости раствора η = η0 = 50 сП. С учетом (1), значение нано-вязкости η, соответствующей движению НЧ в среде с заданным значением φБСА, может быть получено из:

(3)
$\eta = \frac{{{{{\eta }}_{0}}{{{\Gamma }}_{0}}}}{{\Gamma }},$
где η0 – вязкость простого раствора с такой же макроскопической вязкостью, ΔΓ0 – уширение спектра НЧ в простом растворе, ΔΓ – уширение спектра НЧ, диспергированных в исследуемой среде ММК. Значение нано-вязкости для сред с φБСА = 5% и φБСА = 10% составило η5 = 68.2 ± 12.4 сП и η10 = 77.6 ± 10.7 сП соответственно (рис. 2).

Рис. 2.

Рассчитанные на основании анализа мёссбауэровских спектров значения нано-вязкости, соответствующей движению НЧ в исследуемых модельных средах. Представлены значения для сред с φБСА 0, 5 и 10%. Макроскопическая вязкость всех сред η0 составляла 50 ± 2 сП. Вязкости соответствуют температуре сред T = 276.0 ± 0.1 К.

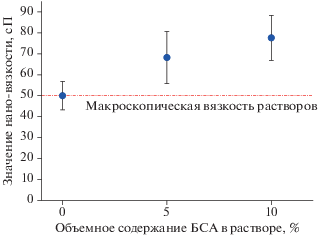
Таким образом, установлено, что даже в отсутствие клеточных структурных единиц эффект ММК изменяет броуновское движение наноразмерных объектов. Значение нано-вязкости в растворе с объемным содержанием 10% макромолекул, оказалась в 1.5 раза выше значения его макроскопической вязкости. Следует отметить, что разработанный подход для исследования нано-вязкости может быть применен для любых других НЧ вне зависимости от их формы, размера и химии поверхности.

ЗАКЛЮЧЕНИЕ

Впервые методом мёссбауэровской спектроскопии проведено исследование наномасштабного движения в условиях макромолекулярного краудинга. Обнаружено, что наличие макромолекул в растворе в наносекундном диапазоне измерений замедляет среднюю скорость броуновского движения наночастиц. Данный эффект возрастает с повышением концентрации макромолекул в растворе.

Работа частично поддержана РФФИ в рамках комплексного научного проекта № 17-00-00444 (К): изготовление образцов выполнено в рамках подпроекта № 17-00-00442, мёссбауэровские исследования выполнены в рамках подпроекта № 17-00-00438, математический анализ выполнен в рамках подпроекта № 17-00-00443 и частично в рамках государственного задания ФТИАН им. К.А. Валиева РАН Минобрнауки РФ по теме № 0066-2019-0004.

Список литературы

  1. Goins A.B., Sanabria H., Waxham M.N. // Biophys. J. 2008. V. 95. № 11. P. 5362.

  2. Einstein A. // Ann. Phys. 1905. V. 17. P. 549.

  3. Smoluchowski M. // Ann. Phys. 1906. V. 21. P. 756.

  4. Hofling F., Franosch T. // Rep. Prog. Phys. 2013. V. 76. Art. № 046602.

  5. Dix J.A., Verkman A.S. // Ann. Rev. Biophys. 2008. V. 37. P. 247.

  6. Ellis R.J., Minton A.P. // Nature. 2003. V. 425. № 6953. P. 27.

  7. Di Rienzo C., Piazza V., Gratton E. et al. // Nat. Commun. 2014. V. 5. № 1. P. 1.

  8. Elcock A.H. // Curr. Opin. Struct. Biol. 2010. V. 20. № 2. P. 196.

  9. Minton A.P. // J. Cell. Sci. 2006. V. 119. № 14. P. 2863.

  10. Qin S., Zhou H.X. // Biophys. J. 2009. V. 97. № 1. P. 12.

  11. Roosen-Runge F., Hennig M., Zhang F. et al. // PNAS. 2011. V. 108. № 29. Art. № 11815.

  12. Novak I.L., Kraikivski P., Slepchenko B.M. et al. // Biophys. J. 2009. V. 97 № 3. P. 758.

  13. Rivas G., Minton A.P. // Trend. Biochem. Sci. 2016. V. 41. № 11. P. 970.

  14. Rashid R., Chee S.M., Raghunath M., Wohland T. // Phys. Biol. 2015. V. 12. № 3. Art. № 034001.

  15. Weiss M. // Phys. Rev. E. 2013. V. 88. № 1. Art. № 010101.

  16. Ernst D., Hellmann M., Köhler J., Weiss M. // Soft Matt. 2012. V. 8. № 18. P. 4886.

  17. Guigas G., Kalla C., Weiss M. // Biophys. J. 2007. V. 93. № 1. P. 316.

  18. Norregaard K., Metzler R., Ritter C.M. et al. // Chem. Rev. 2017. V. 117. № 5. P. 4342.

  19. Чуев М.А., Черепанов В.М., Поликарпов М.А. // Письма в ЖЭТФ. 2018. Т. 108. № 1. С. 57; Chuev M.A., Cherepanov V.M., Polikarpov M.A. // JETP Lett. 2018. V. 108. № 1. P. 59.

  20. Gabbasov R., Yurenya A., Nikitin A. et al. // JMMM. 2019. V. 475. P. 146.

  21. Landers J., Salamon S., Remmer H. et al. // Nano Lett. 2016. V. 16. № 2. P. 1150.

  22. Keller H., Kündig W. // Sol. St. Commun. 1975. V. 16. № 2. P. 253.

  23. Черепанов В.М., Габбасов Р.Р., Юреня А.Ю. и др. // Крист. 2020. Т. 65. № 3. С. 414.

  24. Kuimova M.K., Yahioglu G., Levitt J.A. et al. // J. Amer. Chem. Soc. 2008. V. 130. № 21. P. 6672.

  25. Garanina A.S., Naumenko V.A., Nikitin A.A. et al. // Nanomed. 2020. V. 25. Art. № 102171.

  26. Priev A., Almagor A., Yedgar S. et al. // Biochem. 1996. V. 35. № 7. P. 2061.

  27. Chuev M.A. // JMMM. 2019. V. 470. P. 12.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал