Известия РАН. Серия физическая, 2020, T. 84, № 2, стр. 229-232

ВВЕДЕНИЕ

Все больший интерес вызывают исследования, посвященные методам генерации терагерцового излучения. Принято включать в этот диапазон электромагнитные частоты от 0.1 до 10 ТГц. Сигналы в диапазоне ТГц сегодня находят множество применений в обработке изображений, системах безопасности, астрономии, биологии, медицине и других областях [1]. Один из наиболее эффективных методов генерации такого излучения заключается в использовании механизма оптического выпрямления. В этом случае, спектр ТГц сигнала является широкополосным, т.е. спектральная ширина импульса соизмерима со средней частотой спектра. Ширина генерируемого импульса такова, что он охватывает около одного периода колебаний ТГц диапазона. Таким образом, при оптическом методе генерации ТГц-сигнал обладает свойствами ультракороткого импульса. Это означает, что приближение медленно меняющейся огибающей неприменимо для описания таких импульсов.

Сущность упомянутого выше оптического метода генерации широкополосного ТГц-излучения в квадратично нелинейных средах, основанного на эффекте оптического выпрямления, заключается в следующем: в нелинейную среду подается фемтосекундный оптический импульс, спектр которого содержит частоты, на разности которых может быть сформировано ТГц-излучение. Условие генерации может быть получено из законов сохранения импульса и энергии для элементарных событий рассеяния. Если длительность оптического импульса составляет 3–5 колебаний, то еще можно использовать понятие огибающей [2]. Для описания таких импульсов допустимо использовать уравнения, которые можно рассматривать как обобщение известной системы Ядзимы–Ойкавы [3]. Эту систему следует дополнить членами, содержащими высшие производные по времени огибающей оптического импульса и электрического поля терагерцового сигнала для линейной и нелинейной дисперсии, а также дифракции. Поскольку генерируемый терагерцовый сигнал является широкополосным в спектральном смысле, т.е. содержит около одного периода электромагнитных колебаний, понятие огибающей к нему больше неприменимо. Поэтому уравнение для терагерцовой составляющей содержит не огибающую, а электрическое поле самого импульса.

В работе [4] продемонстрирована возможность генерации как широкополосных, так и квазимонохроматических терагерцовых сигналов. Выявлены условия, при которых эффективность генерации фазомодулированного наносекундного оптического импульса больше, чем спектрально ограниченного фемтосекундного сигнала. В [5] авторами разработано интегрируемое обобщение системы уравнений Ядзимы–Ойкавы для описания оптической генерации широкополосного терагерцового излучения в квадратично нелинейной среде с учетом влияния фазы оптического импульса на этот процесс. В [6] исследован процесс оптического выпрямления в системе резонансных анизотропных молекул с постоянным дипольным моментом. В этой работе продемонстрировано, что генерация ТГц-излучения происходит в режиме филаментации, причем, из филамент формируются устойчивые оптико-терагерцовые пули. Как показано в работе [7], генерация терагерцового излучения в планарном волноводе сопровождается филаментацией оптической и терагерцовой составляющих и стабильные оптические терагерцовые пространственно-временные солитоны не образуются. В [8] исследована оптическая методика генерации широкополосного терагерцового излучения в градиентном волноводе. Рассмотрены явления захвата оптических и терагерцовых импульсов в волноводе и показано, что захват происходит в условиях филаментации как с нормальной, так и с аномальной групповой дисперсией оптического сигнала.

В настоящей работе с помощью численного моделирования исследован процесс генерации терагерцового излучения малопериодным оптическим импульсом. В качестве модели использовано обобщение системы Ядзимы–Ойкавы. Укорачивая длительность импульса, мы предполагаем сближение дифракционных длин оптической и терагерцовой компоненты и, тем самым, рассчитываем получить устойчивые оптико-терагерцовые пули.

ПОСТАНОВКА ЗАДАЧИ

Уравнения, описывающие огибающую оптического излучения $\Psi $ и электрическое поле возникающего терагерцового импульса ${{E}_{T}}$ в коллинеарном режиме генерации с учетом малой длительности оптического импульса принимают вид:

где $z,$ $x$ – продольная и поперечная координаты распространения, ${\tau } = t - {z \mathord{\left/ {\vphantom {z {{{{v}}_{g}}}}} \right. \kern-0em} {{{{v}}_{g}}}}$ = $t - {z \mathord{\left/ {\vphantom {z {{{v}_{T}}}}} \right. \kern-0em} {{{v}_{T}}}},$ ${\omega }$ – несущая частота оптического импульса, ${{k}_{{2,3}}}$ – коэффициенты дисперсии второго и третьего порядков оптического излучения, ${\alpha }$ – коэффициент дисперсии третьего порядка терагерцового излучения, $a,$ $b,$ ${\mu },$ ${\beta },$ ${\sigma },$ $q$ – коэффициенты нелинейности, ${{g}_{{\omega }}}(x)$ и ${{g}_{T}}(x)$ – зависимость показателя преломления оптического и терагерцового излучения от поперечной координаты, обусловленная волноводом, $c$ – скорость света, ${{n}_{{\omega }}}$ и ${{n}_{T}}$ – показатели преломления оптического и терагерцового излучения вблизи центра пучка. В работе рассматривали параболический профиль волновода: ${{g}_{{{\omega },\,T}}}\left( x \right) = \frac{{2{\pi }}}{{c{{n}_{{{\omega },\,T}}}}}{{x}^{2}}.$

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ

Для численного решения данная система была обезразмерена:

где $\psi = \bar {\psi }{{\psi }_{0}}$, ${{E}_{T}} = {{\bar {E}}_{T}}{{\psi }_{0}}$, ${{\psi }_{0}},$ $\tau = \bar {\tau }{{\tau }_{0}},$ $z = \bar {z}{{l}_{{nl}}},$ $x = \bar {x}{{R}_{0}},$ ${{l}_{{nl}}} = {1 \mathord{\left/ {\vphantom {1 {\left( {a{{\psi }_{0}}} \right)}}} \right. \kern-0em} {\left( {a{{\psi }_{0}}} \right)}},$ ${{D}_{{k2}}} = sign({{k}_{2}})\frac{{{{l}_{{nl}}}}}{{{{l}_{{dis2}}}}},$ ${{D}_{{k3}}} = \frac{{{{l}_{{nl}}}}}{{{{l}_{{dis3}}}}},$ ${{l}_{{dis2}}} = \frac{{2\tau _{0}^{2}}}{{\left| {{{k}_{2}}} \right|}},$ ${{l}_{{dis3}}} = \frac{{6\tau _{0}^{3}}}{{{{k}_{3}}}},$ ${{D}_{b}} = \frac{{b{{\psi }_{0}}}}{{{{\tau }_{0}}}}{{l}_{{nl}}},$ ${{D}_{{\mu }}} = \frac{{\mu {{\psi }_{0}}}}{{{{\tau }_{0}}}}{{l}_{{nl}}},$ ${{D}_{{g{\omega }}}} = \frac{{2\pi \omega {{l}_{{nl}}}}}{{c{{n}_{{\omega }}}}},$ $N = \omega {{\tau }_{0}},$ ${{D}_{{x{\omega }}}} = \frac{{{{l}_{{nl}}}}}{{l_{D}^{{\omega }}}},$ ${{D}_{{\alpha }}} = \frac{{\alpha {{l}_{{nl}}}}}{{\tau _{0}^{3}}},$ ${{D}_{{\beta }}} = \frac{{\beta {{\psi }_{0}}{{l}_{{nl}}}}}{{{{\tau }_{0}}}},$ ${{D}_{{\sigma }}} = \frac{{\sigma {{\psi }_{0}}{{l}_{{nl}}}}}{{{{\tau }_{0}}}},$ ${{D}_{q}} = \frac{{q{{\psi }_{0}}{{l}_{{nl}}}}}{{\tau _{0}^{2}}},$ ${{D}_{{gT}}} = \frac{{2\pi {{l}_{{nl}}}}}{{c{{n}_{T}}{{\tau }_{0}}}},$ ${{D}_{{xT}}} = \frac{{{{l}_{{nl}}}}}{{l_{D}^{T}}},$ $l_{D}^{{\omega }} = \frac{{{{n}_{{\omega }}}\omega }}{c}R_{0}^{2}$ и $l_{D}^{T} = \frac{{2{{n}_{T}}}}{{c{{\tau }_{0}}}}R_{0}^{2}$ – дифракционные длины оптического и терагерцового излучения, ${{{\tau }}_{0}}$ и ${{x}_{0}}$ – начальные длительность и ширина оптического импульса. В дальнейшем описании опустим черточки при обозначении безразмерных величин. В наших расчетах мы положили равными ${{{\tau }}_{0}} = {{x}_{0}} = 1,$ т.е. расчетные координаты нормированы на начальные длительность и ширину.

Начальный профиль оптического импульс задавали в гауссовом виде $\psi (z = 0)$ = $\exp \left( { - {{x}^{2}} - {{\tau }^{2}}} \right).$ Терагерцовая компонента на вход не подается, ${{E}_{T}}(z = 0) = 0,$ она генерируется в процессе распространения.

В работах [7, 8] показано, что длительные оптико-терагерцовые импульсы подвержены филаментации. В данной работе ведется поиск солитоно-подобного решения. Для этого уменьшается число осцилляций импульса $N$.

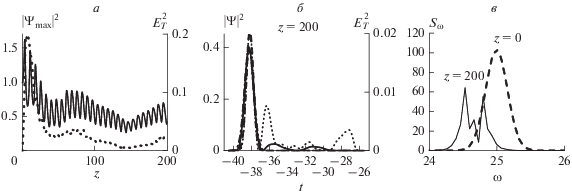
Проведено численное моделирование для случая квазимонохроматического импульса с $N = 25.$ Использовали следующие параметры ${{D}_{{k2}}} = 0.05,$ ${{D}_{{k3}}} = 0.00166,$ ${{D}_{b}} = 0.1,$ ${{D}_{\mu }} = 0.1,$ ${{D}_{{g\omega }}} = - 1,$ D_xω = = 0.05, ${{D}_{\alpha }} = 0.01,$ ${{D}_{\beta }} = 0.1,$ ${{D}_{\sigma }} = 0.1,$ ${{D}_{q}} = 0.01,$ ${{D}_{{gT}}} = - 0.05,$ ${{D}_{{xT}}} = 0.005.$ На рис. 1 представлены результаты моделирования. Интенсивность генерируемой терагерцовой компоненты много меньше оптической, но при этом максимумы компонент совпадают, их профили в целом близки к гауссовым. Возникший импульс распространяется как целое, испытывая осцилляции. Однако значительная часть и оптической, и терагерцовой компонент отстает от основного импульса. Спектр оптической компоненты смещается в область низких частот. Это можно объяснить тем, что при генерации терагерцового излучения квант исходного излучения распадается на квант терагерцового излучения и квант оптического, с длиной волны больше исходного. Спектр оптического излучения имеет форму, сильно отличающуюся от первоначальной. Все вышеизложенное свидетельствует о том, что возникающий импульс не является солитоном, хотя и более близок к устойчивому решению, чем длительный оптико-терагерцовый импульс.

Для получения солитоно-подобного решения число осцилляций начального импульса $N$ уменьшено. Поскольку квазиоптическое приближение справедливо при $N \geqslant 3 - 5,$ проанализирован вариант $N = 5.$ Все остальные параметры остались неизменными. Результаты моделирования приведены на рис. 2. Интенсивность компонент претерпевает осцилляции, но в целом, импульс распространяется в солитоно-подобном режиме. Профили оптической и терагерцовой компоненты на расстоянии $z = 200$ хорошо аппроксимируются гауссовым профилем. Сравнение спектров оптического излучения на начальном этапе и при $z = 200$ показывает, что спектр смещается в область низких частот. Форма спектра в целом сохраняется, хотя и имеет место некоторое уменьшение его ширины и увеличение максимальной интенсивности.

Исходя из приведенных расчетов, можно сделать вывод, что генерация терагерцового излучения более эффективна импульсами короткой длительности. При этом происходит некратное понижение оптической частоты.

ЗАКЛЮЧЕНИЕ

В работе рассмотрена генерация оптико-терагерцового импульса в квадратично-нелинейном волноводе. С помощью численного моделирования найдено решение в солитоно-подобном виде. Показано, что с уменьшением числа осцилляций входящего оптического импульса возникающий оптико-терагерцовый импульс ближе к солитону.

Исследование выполнено за счет гранта Российского научного фонда № 17-11-01157.