1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 84, № 3, 2020

Известия РАН. Серия физическая, 2020, T. 84, № 3, стр. 382-386

Эволюция квантовых поляризационных состояний света в кристаллах с регулярной доменной структурой

А. В. Белинский 1, Р. Сингх 1, *

1 Федеральное государственное бюджетное образовательное учреждение высшего образования “Московский государственный университет имени М.В. Ломоносова”, физический факультет
Москва, Россия

* E-mail: ranjit.singh@mail.ru

Поступила в редакцию 20.09.2019
После доработки 15.11.2019
Принята к публикации 27.11.2019

Полный текст (PDF)

Аннотация

Исследована эволюция ортогонально-поляризационных мод света в кристаллах с регулярной доменной структурой и квадратичной нелинейностью. Численно получены результаты квантового описания для больших длин взаимодействия. Установлено, что корреляционные коэффициенты второго порядка и степень поляризации по длине взаимодействия изменяются немонотонно. Показано, что степень поляризации ортогонально-поляризационных мод отлична от нуля. Обнаружено, что степень перепутанности изменяется немонотонно.

ВВЕДЕНИЕ

Обычно для приготовления квантовых поляризационных состояний света используются монодоменные нелинейные оптические кристаллы с квадратичной и кубической нелинейностью [1–9], но в последнее время растет интерес и к кристаллам с регулярной доменной структурой (РДС) [10–12]. Он связан с тем, что появляется дополнительная возможность реализации того или иного типа фазового синхронизма. В результате в одном и том же кристалле одновременно могут происходить различные нелинейные процессы, например, параметрическое рассеяние света и генерация суммарных гармоник.

Квантовые поляризационные характеристики света играют важную роль в задачах квантовой оптики и информатики. Обычно для изучения поляризационных характеристик света применяются наблюдаемые операторы Стокса, Джонса и их дисперсии. В работе [10] были рассмотрены параметрический процесс и суммарная генерация вырожденных мод в РДС-кристалле в приближении заданного поля, когда мода накачки 2e на частоте $2{{\omega }_{e}}$ не истощается, и были получены аналитические решения для систем линеаризованных операторных уравнений движения. В данной работе при расчетах используется более точный метод диагонализации гамильтониана взаимодействия [11], с использованием которого были вычислены коэффициенты корреляции между парными модами, степень поляризации и перепутанности. Метод позволяет анализировать квантовые статистические характеристики всех взаимодействующих мод на любых длинах взаимодействия.

НЕЛИНЕЙНЫЕ ПРОЦЕССЫ В РДС-КРИСТАЛЛЕ И ИХ ОПИСАНИЕ

Рассмотрим 4 плоские монохроматические моды с кратными частотами ${{\omega }_{{1o}}},$ ${{\omega }_{{1e}}},$ $2{{\omega }_{{2e}}},$ $3{{\omega }_{{3e}}},$ характеризуемые операторами уничтожения фотона ${{\hat {a}}_{{1o}}},$ ${{\hat {a}}_{{1e}}},$ ${{\hat {a}}_{{2e}}}$ и ${{\hat {a}}_{{3e}}},$ которые коллинеарно распространяются внутри РДС-кристалла с квадратичной нелинейностью. Операторы удовлетворяют стандартным коммутационным соотношениям: $\left[ {{{{\hat {a}}}_{{jp}}},\hat {a}_{{j{\kern 1pt} 'p{\kern 1pt} '}}^{ + }} \right] = {{\delta }_{{jp,j{\kern 1pt} 'p{\kern 1pt} '}}}$ ($p,p{\kern 1pt} ' = o$ – обыкновенная волна, и $p,p{\kern 1pt} ' = e$ – необыкновенная волна). Одновременно происходят два процесса: параметрическая генерация субгармоник (тип II) и преобразование частоты вверх за счет суммирования частот субгармоник с частотой накачки [10]:

(1a)
$\begin{gathered} 2{{\omega }_{e}} = {{\omega }_{o}} + {{\omega }_{e}},\,\,\,\,\delta {{k}_{1}} = {{k}_{{2e}}} - {{k}_{{1o}}} - {{k}_{{1e}}} + \\ + \,\,{{m}_{1}}{{G}_{1}} = \Delta {{k}_{1}} + {{m}_{1}}{{G}_{1}}, \\ \end{gathered} $
(1b)
$\begin{gathered} {{\omega }_{o}} + 2{{\omega }_{e}} = 3{{\omega }_{e}},\,\,\,\,\delta {{k}_{2}} = {{k}_{{3e}}} - {{k}_{{1o}}} - {{k}_{{2e}}} + \\ + \,\,{{m}_{2}}{{G}_{2}} = \Delta {{k}_{2}} + {{m}_{2}}{{G}_{2}}, \\ \end{gathered} $
где ${{k}_{{jp}}}$ – абсолютные значения волновых векторов соответствующих мод с частотами ${{\omega }_{{jp}}};$ $j = 1,2,3;$ $\Delta {{k}_{q}}$ – волновые расстройки соответствующего процесса для однородного кристалла; $~q = 1,2;$ ${{m}_{q}} = \pm 1, \pm 3, \pm 5, \ldots $ – порядки квазисинхронизма; ${{G}_{q}} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {{{\Lambda }_{q}}}}} \right. \kern-0em} {{{\Lambda }_{q}}}}$– волновое число (модуль “псевдовектора” решетки доменной структуры с периодом ${{{\Lambda }}_{q}}$). Выполнение условия квазисинхронизма в РДС-кристалле LiNbO3 [10] для процессов (1a) и (1b) соответствует $\delta {{k}_{q}} = 0.$

Гамильтониан взаимодействия рассматриваемых процессов имеет вид [10]:

(2)
${{\hat {H}}_{{{\text{int}}}}} = \hbar \left( {{{\gamma }_{1}}{{{\hat {a}}}_{{1o}}}{{{\hat {a}}}_{{1e}}}\hat {a}_{{2e}}^{ + } + {{\gamma }_{2}}{{{\hat {a}}}_{{1o}}}{{{\hat {a}}}_{{2e}}}\hat {a}_{{3e}}^{ + }} \right) + {\text{э}}.\,{\text{с}}.$
где $\hbar $ – постоянная Планка, ${{\gamma }_{{1,2}}}$ – коэффициенты нелинейного взаимодействия, э.с. – эрмитово сопряжение$.~$ Это приближение плоских монохроматических мод при коллинеарном взаимодействии. Поперечная пространственная структура пучков при этом полагается однородной.

Выполним диагонализацию гамильтониана взаимодействия (2) и найдем его собственные векторы и собственные значения [11]. Затем вычислим оператор эволюции и матрицу плотности $\hat {\rho }\left( \zeta \right) = \hat {U}\left( \zeta \right)\hat {\rho }\left( 0 \right){{\hat {U}}^{ + }}\left( \zeta \right).~$ Здесь $\hat {\rho }\left( 0 \right) = \left| {{{\psi }_{0}}} \right\rangle \left\langle {{{\psi }_{0}}} \right|$ – матрица плотности начального состояния для всех мод на входе РДС-кристалла. Для расчетов удобно ввести приведенную длину взаимодействия $\zeta = {{\gamma }_{1}}z$ и безразмерный коэффициент нелинейного взаимодействия $\xi = {{{{\gamma }_{2}}} \mathord{\left/ {\vphantom {{{{\gamma }_{2}}} {{{\gamma }_{1}}}}} \right. \kern-0em} {{{\gamma }_{1}}}}.$ Результаты будут представлены далее.

СТАТИСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОЛЯРИЗАЦИОННЫХ МОД

Для изучения поляризационных характеристик ортогональных мод 1о и 1е вычисляются, как это принято [1–6, 8, 11, 12], значения среднего числа фотонов

${{N}_{{jp}}}\left( \zeta \right) = \left\langle {\hat {a}_{{jp}}^{ + }\left( \zeta \right){{{\hat {a}}}_{{jp}}}\left( \zeta \right)} \right\rangle ,$

коэффициентов корреляции фотонов между разными модами

(3.1)
$g_{{jpj{\kern 1pt} 'p{\kern 1pt} '}}^{{\left( 2 \right)}}\left( \zeta \right) = \frac{{\left\langle {\hat {a}_{{jp}}^{ + }\left( \zeta \right){{{\hat {a}}}_{{jp}}}\left( \zeta \right)\hat {a}_{{j{\kern 1pt} 'p{\kern 1pt} '}}^{ + }\left( \zeta \right){{{\hat {a}}}_{{j{\kern 1pt} 'p{\kern 1pt} '}}}\left( \zeta \right)} \right\rangle }}{{{{N}_{{jp}}}\left( \zeta \right){{N}_{{j{\kern 1pt} 'p{\kern 1pt} '}}}\left( \zeta \right)}},$

и $g_{{jpj{\kern 1pt} 'p{\kern 1pt} '}}^{{\left( 2 \right)}}\left( \zeta \right)$ без нормировочного множителя $\left( {{{N}_{{jp}}}\left( \zeta \right){{N}_{{j{\kern 1pt} 'p{\kern 1pt} '}}}\left( \zeta \right)} \right)$

(3.2)
$g_{{jpj{\kern 1pt} 'p{\kern 1pt} '}}^{{'\left( 2 \right)}}\left( \zeta \right) = \left\langle {\hat {a}_{{jp}}^{ + }\left( \zeta \right){{{\hat {a}}}_{{jp}}}\left( \zeta \right)\hat {a}_{{j{\kern 1pt} 'p{\kern 1pt} '}}^{ + }\left( \zeta \right){{{\hat {a}}}_{{j{\kern 1pt} 'p{\kern 1pt} '}}}\left( \zeta \right)} \right\rangle ,$

среднего значения операторов Стокса

${{\hat {S}}_{{0,1}}}\left( \zeta \right) = \hat {a}_{{1o}}^{ + }\left( \zeta \right){{\hat {a}}_{{1o}}}\left( \zeta \right) \pm \hat {a}_{{1e}}^{ + }\left( \zeta \right){{\hat {a}}_{{1e}}}\left( \zeta \right),$
${{\hat {S}}_{2}}\left( \zeta \right) = \hat {a}_{{1o}}^{ + }\left( \zeta \right){{\hat {a}}_{{1e}}}\left( \zeta \right) + \hat {a}_{{1e}}^{ + }\left( \zeta \right){{\hat {a}}_{{1o}}}\left( \zeta \right),$
${{\hat {S}}_{3}}\left( \zeta \right) = i\hat {a}_{{1e}}^{ + }\left( \zeta \right){{\hat {a}}_{{1o}}}\left( \zeta \right) - \hat {a}_{{1o}}^{ + }\left( \zeta \right){{\hat {a}}_{{1e}}}\left( \zeta \right),$

степени поляризации взаимодействующих ортогональных мод [5, 8]

(4)
$PoD\left( \zeta \right) = \sqrt {\frac{{\sum\limits_{k = 1}^3 {{{{\hat {S}}}_{k}}{{{\left( \zeta \right)}}^{2}}} }}{{\sum\limits_{k = 1}^3 {\hat {S}_{k}^{2}\left( \zeta \right)} }}} .$

Операторы Стокса $\hat {S}_{{0,1,2,3}}^{{}}\left( \zeta \right)$ удовлетворяют следующим коммутационным соотношениям:

$\begin{gathered} \left[ {{{{\hat {S}}}_{0}}\left( \zeta \right),{{{\hat {S}}}_{j}}\left( \zeta \right)} \right] = 0,\,\,\,\,\left[ {{{{\hat {S}}}_{j}}\left( \zeta \right),{{{\hat {S}}}_{k}}\left( \zeta \right)} \right] = 2i{{{\hat {S}}}_{l}}\left( \zeta \right), \\ \left( {j,k,l = 1,2,3} \right). \\ \end{gathered} $

Соотношение неопределенности для операторов Стокса имеет вид

${\Delta }\hat {S}_{j}^{2}\left( \zeta \right){\Delta }\hat {S}_{k}^{2}\left( \zeta \right) \geqslant {{\left| {{{{\hat {S}}}_{l}}\left( \zeta \right)} \right|}^{2}},\,\,\,\,\left( {j \ne k \ne l} \right).$

МЕРЫ ПЕРЕПУТАННОСТИ МЕЖДУ МОДАМИ

Для определения степени перепутанности рассматриваются разные меры перепутанности [14‒22], например, конкарренс (concurrence), параметр Шмидта, энтропия фон Неймана. Их можно применять в соответствии с удобством вычисления и особенностями рассматриваемой физической задачи. В данной работе рассматриваются параметр Шмидта и энтропия фон Неймана. Формулы для вычисления значения параметра Шмидта [9, 16, 17] и энтропии фон Неймана [14, 15, 18–21] имеют следующий вид

(5)
$K = \frac{1}{{\sum \eta _{m}^{2}}},$
(6)
$S = - \sum {{\eta }_{m}}{{\log }_{2}}{{\eta }_{m}},$
где ${{\eta }_{m}}$ – собственные значения редуцированной матрицы плотности ${{\hat {\rho }}_{{1o}}}\left( \zeta \right).$

Для вычисления значения мер перепутанности (5), (6) между поляризационными модами 1o и (1e, 2e, 3e) необходимо вычислить матрицу плотности полной системы $\hat {\rho }\left( \zeta \right),$ которая будет зависит от приведенной длины взаимодействия $\zeta .$ Затем нужно редуцировать ее последовательно по подсистемам мод 3e, 2e и 1e. В результате получим редуцированную матрицу плотности ${{\hat {\rho }}_{{1o}}}\left( \zeta \right)$ подсистемы 1o. Далее необходимо найти собственные значения редуцированной матрицы подсистемы 1o.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Расчеты проводили при, $\xi = 0.7,$ а на входе $(\zeta = 0$) РДС-кристалла моды 1o, 1e и 3е полагали в вакуумном состоянии $\left| 0 \right\rangle ,$ накачка $2e$ – в когерентном состоянии со средним числом фотонов ${{\left| {{{\alpha }_{{2e}}}} \right|}^{2}} = 6$ и фазой ${{\varphi }_{{2e}}} = \pi {\text{/}}3,$ т.е., $\left| {{{\psi }_{0}}} \right\rangle $ = = $\left| 0 \right\rangle \left| 0 \right\rangle \left| {{{\alpha }_{{2e}}}} \right\rangle \left| 0 \right\rangle .$

Отметим, что в случае РДС-кристалла обнаружена сильная (>1) корреляция (3.1) между разными поляризационными парными модами (1e, 1o), (1e, 3e), (1o, 3e) и (2e, 3e) при определенных длинах взаимодействий и начальных условиях (см. рис. 1). Корреляции между остальными модами (1o, 2e) и (1e, 2e) < 1, поэтому они опущены. Дополнительную корреляцию между модами (1e, 3e), (1o, 3e) и (2e, 3e) можно использовать для обработки и восстановления фантомных изображений, а в монодоменных кристаллах она отсутствует.

Рис. 1.

Коэффициент корреляции ${{g}^{{\left( 2 \right)}}},$ когда мода ${{2}_{e}}$ истощалась и находилась в когерентном состоянии, а другие моды $1o,1e,3e$ – в вакуумном состоянии.

В монодоменных кристаллах степень поляризации равна нулю за счет существования только одного процесса (1a) и неопределенности фазы между модами 1o и 1e. При этом среднее значение фотонов в модах 1o и 1e равны, но средние значения операторов Стокса при вырожденном параметрическом рассеянии (1a) для монодоменного кристалла нулевые (${{\hat {S}}_{{1,2,3}}} = 0$), и в результате степень поляризации также равна нулю. В рассматриваемом РДС-кристалле значение степени поляризации (4) не равно нулю и имеет немонотонный характер (рис. 2). Это связано с тем, что задействованы два процесса (1a и 1b), и ${{\hat {S}}_{1}} \ne 0,$ ${{\hat {S}}_{{2,3}}} = 0.$ Кроме неопределенности фазы между модами 1o и 1e, существенный вклад в поляризацию вносит процесс (1b), и степень поляризации становится отличной от нуля (рис. 2).

Рис. 2.

Степень поляризации (PoD) мод $1o,1e,$ когда мода 2e истощалась и находилась в когерентном состоянии, а другие моды $1o,1e,3e$ – исходно в вакуумном состоянии.

Рисунок 3 иллюстрирует динамику степени перепутанности. Видно, что поведение кривых похоже для параметров (5) и (6). Поэтому достаточно описать поведение одного. Почти осциллирующий характер кривых иллюстрируют то, что значения степени перепутанности зависят от приведенной длины взаимодействия при рассматриваемых начальных условиях. Отметим, что K – параметр Шмидта для перепутанных состояний >1, для неперепутанных – единица, а энтропия фон Неймана, соответственно, положительна (для перепутанных) или равна нулю (для неперепутанных).

Рис. 3.

Степень перепутанности мод 1o и (1e, 2e, 3e), когда мода 2e истощалась и находилась в когерентном состоянии, а другие моды 1o, 1e, 3e – исходно в вакуумном состоянии.

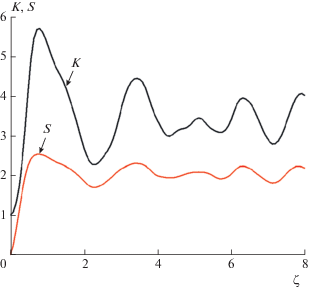
На рис. 4 показаны зависимости для ${{g}^{{'\left( 2 \right)}}}$ (3.2) и степени перепутанности, которые весьма похожи. Осциллирующий характер кривых связан с конкуренцией между процессами 1a и 1b.

Рис. 4.

Зависимости для корреляций ${{g}^{{'\left( 2 \right)}}}$ (без нормировочного множителя) и степени перепутанности мод 1o и (1e, 2e, 3e), когда мода 2e истощалась и находилась в когерентном состоянии, а другие моды 1o, 1e, 3e – исходно в вакуумном состоянии.

Дополнительная корреляция между модами (1o, 3e), (1e, 3e), степень поляризации и степень перепутанности могут потенциально расширить возможность восстановления фантомных изображений с помощью методов поляриметрии [12, 13] и также в протоколах квантовой криптографии, в частности, BB84 и E91.

Учет истощения накачки по сравнению с работой [10] позволяет описывать новые эффекты, связанные с осциллирующим характером зависимостей для эволюции поляризационных характеристик излучения по длине взаимодействия. Напомним, что в [10] обнаружено одновременное подавление дисперсий всех операторов Стокса в случае, когда мода 2e полагалась неистощимой, а 3e на входе была в вакуумном состоянии, моды 1o, 1e – в когерентном состоянии со средним числом фотонов 1. В [10] не были исследованы коэффициенты корреляции мод, степень поляризации и степень перепутанности. В данной работе нам удалось восполнить эти пробелы и обобщить алгоритм расчета на случай истощающейся накачки.

По-видимому, используемая при расчетах интенсивность накачки (6 фотонов на моду) является недостаточной для полномасштабного изучения эволюции излучения в нелинейной среде. К сожалению, имеющиеся компьютерные мощности не позволили исследовать более приближенные к реальности начальные условия. Однако описанный алгоритм расчета принципиально пригоден для любой интенсивности излучения. Кроме того, намеченные тенденции сохраняются при увеличении числа фотонов на моду накачки, например, от 3 до 6. Вероятно они сохранятся и при более интенсивной накачке.

Работа выполнена при поддержке РФФИ (грант № 18-01-00598А).

Список литературы

  1. Чиркин А.С., Орлов А.А., Паращук Д.Ю. // Квант. электрон. 1993. Т. 20. № 10. С. 999.

  2. Карасев В.П., Масалов А.В. // Опт. и спектроск. 1993. Т. 74. № 6. С. 928.

  3. Chirkin A.S., Beskrovnyi V.N. // Las. Opt. 1998. V. 8. № 3. P. 709.

  4. Соколов А.Л., Масалов А.В. // Опт. и спектроск. 2011. Т. 111. № 6. С. 883.

  5. Чиркин А.С. // Опт. и спектроск. 2015. Т. 119. № 3. С. 397; Chirkin A.S. // Opt. Spectrosс. 2015. V. 119. № 3. P. 371.

  6. Бушев П.А., Карасев В.П., Масалов А.В. и др. // Опт. и спектроск. 2001. Т. 91. № 4. С. 558; Bushev P.A., Karassiov V.P., Masalov A.V. et al. // Opt. Spectrosс. 2001. V. 91. № 4. P. 526.

  7. Карасев В.П., Масалов А.В. // ЖЭТФ. 2004. Т. 126. № 1. С. 63; Karassiov V.P., Masalov A.V. // JETP. 2004. V. 99. P. 51.

  8. Алоджанц А.П., Аракелян С.М., Чиркин А.С. // ЖЭТФ. 1995. Т. 108. № 1. С. 63.

  9. Fedorov M.V., Volkov. P.A., Mikhailova J.M. et al. // New J. Phys. 2011. V. 13. Art. № 083004.

  10. Dmitriev V.G., Singh R. // Int. J. Quant. Inform. 2003. V. 1. № 3. P. 403.

  11. Белинский А.В., Сингх Р. // Квант. электрон. 2018. Т. 48. № 7. С. 611; Belinsky A.V., Singh R. // Quant. Electron. 2018. V. 48. № 7. P. 611.

  12. Чиркин А.С. // Письма в ЖЭТФ. 2016. Т. 103. № 4. С. 309: Chirkin A.S. // JETP Lett. 2016. V. 103. P. 282.

  13. Chirkin A.S., Gostev P.P., Agapov D.P. et al. // Las. Phys. Lett. 2018. V. 15. № 11. Art. № 115404.

  14. Chirkin A.S. // J. Opt. B. 2002. V. 4. № 3. P. S9.

  15. Nikandrov A.V., Chirkin A.S. // J. Russ. Las. Res. 2002. V. 23. № 1. P. 81.

  16. Fedorov M.V., Volkov P.A., Mikhailova J.M. // Phys. Rev. A. 2011. V. 84. Art. № 032335.

  17. Fedorov M.V., Volkov P.A., Mikhailova J.M. // Phys. Rev. A. 2008. V. 78. Art. № 062327.

  18. Баргатин И.В., Гришанин Б.А., Задков В.Н. // УФН. 2001. Т. 171. № 6. С. 625; Bargatin I.V., Grishanin B.A., Zadkov V.N. // Phys. Usp. 2001. V. 44. P. 597.

  19. Кадомцев Б.Б. Динамика и информация. М.: УФН, 1997. 397 с.

  20. Валиев К.А. // УФН. 2005. Т. 175. № 1. С. 3; Vali-ev K.A. // Phys. Usp. 2005. V. 48. № 1. P. 1.

  21. Килин С.Я. // УФН. 1999. Т. 169. № 5. С. 507; Kilin S.Ya. // Phys. Usp. 1999. V. 42. № 5. P. 435.

  22. Wootters W.K. // Phys. Rev. Lett. 1998. V. 80. № 10. P. 2245.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал