Известия РАН. Серия физическая, 2020, T. 84, № 8, стр. 1187-1196

ВВЕДЕНИЕ

Низкоэнергетические реакции с участием ядер трития, гелия, лития и бериллия [1] составляют значительную часть изученных и продолжающих изучаться в настоящее время ядерных реакций. Реакции с изотопами Be представляют значительный интерес с нескольких точек зрения. Радиоактивное ядро ⁷Be (с периодом полураспада ${{T}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ = 53 д) является зеркальным по отношению к стабильному ядру ⁷Li, которое можно представить состоящим из α-кластера и тритонного кластера [2–4]. Ядра ⁹Be и ¹⁰Be представляют состоящими из двух α-кластеров и, соответственно из одного и двух внешних (валентных) слабосвязанных нейтронов [5–7]. Знание свойств и волновой функции основного состояния нуклидов бериллия необходимо для теоретического описания реакций с их участием.

Уравнение Шредингера в рамках задачи трех тел с ортогональным проектированием впервые было решено для ядра ⁶Li в работе [8]. В работе [9] уравнение Шредингера для трехтельной системы ⁶Не (n + n + α) было решено с помощью разложений по гиперсферическим функциям. В работах [10, 11] волновые функции системы трех тел были получены с помощью гауссового базиса и численного решения системы интегральных уравнений Хилла–Уилера (Hill−Wheeler). Более простую возможность вычисления энергии ${{E}_{0}}$ и плотности вероятности ${{\left| {{{\Psi }_{0}}\left( {{{{\vec {r}}}_{1}}, \ldots ,{{{\vec {r}}}_{n}}} \right)} \right|}^{2}}$ для основного состояния n-частичной системы дает метод континуальных интегралов Фейнмана [12–17]. Его универсальность позволила в едином подходе выполнить расчеты для ряда малонуклонных ядер: ³H, ^{3, 4, 6}He, ^{6, 7, 11}Li [3, 4, 16, 17]. В данной работе подобные многотельные расчеты проведены для ядер ^{7, 9, 10}Be.

МЕТОД КОНТИНУАЛЬНЫХ ИНТЕГРАЛОВ ФЕЙНМАНА

Энергия ${{E}_{0}}$ и квадрат модуля волновой функции основного состояния ${{\left| {{{\Psi }_{0}}} \right|}^{2}},$ зависящей от координаты q, могут быть найдены с помощью введенных Р. Фейнманом континуальных интегралов (интегралов по траекториям) [12, 13]. Континуальный интеграл (пропагатор) в мнимом (евклидовом) времени $t = - i\tau $ [14, 15] для частицы массой m с потенциальной энергией $V(q)$ можно представить (см. [4, 7]) в виде

Здесь τ = NΔτ и угловыми скобками ❬…❭ обозначено усреднение по случайным $\left( {N - 1} \right)$-мерным векторам (“траекториям”) [7], которое может быть выполнено методом Монте-Карло. Для реализации расчетов средних по случайным траекториям в данной работе использована технология CUDA параллельных вычислений на графических процессорах [18–20]. Расчеты были выполнены на гетерогенном кластере “HybriLIT” [21] Лаборатории информационных технологий Объединенного института ядерных исследований.

Энергии ${{E}_{0}},$ ${{E}_{1}}$ и квадраты модуля волновой функции ${{\left| {{{\Psi }_{0}}(q)} \right|}^{2}},$ ${{\left| {{{\Psi }_{1}}(q)} \right|}^{2}}$ основного и первого возбужденного состояний определяют первые члены асимптотики пропагатора в пределе $\tau \to \infty $ [14, 15]

Для удобства расчетов в масштабах действия ядерных сил удобно использовать безразмерные переменные $\tilde {q} = {q \mathord{\left/ {\vphantom {q {{{x}_{0}}}}} \right. \kern-0em} {{{x}_{0}}}},$ $\tilde {V} = {{V(q)} \mathord{\left/ {\vphantom {{V(q)} {{{\varepsilon }_{0}}}}} \right. \kern-0em} {{{\varepsilon }_{0}}}},$ ${{\tilde {E}}_{0}} = {{{{E}_{0}}} \mathord{\left/ {\vphantom {{{{E}_{0}}} {{{\varepsilon }_{0}}}}} \right. \kern-0em} {{{\varepsilon }_{0}}}}$ $\tilde {m} = {m \mathord{\left/ {\vphantom {m {{{m}_{0}}}}} \right. \kern-0em} {{{m}_{0}}}},$ $\tilde {\tau } = {\tau \mathord{\left/ {\vphantom {\tau {{{t}_{0}}}}} \right. \kern-0em} {{{t}_{0}}}},$ $\Delta \tilde {\tau } = {{\Delta \tau } \mathord{\left/ {\vphantom {{\Delta \tau } {{{t}_{0}}}}} \right. \kern-0em} {{{t}_{0}}}},$ ${{\tilde {K}}_{{\text{E}}}} = {{K}_{{\text{E}}}}{{x}_{0}},$ где ${{x}_{0}} = 1$ фм, ${{\varepsilon }_{0}} = 1$ МэВ, ${{m}_{0}}$ – масса нейтрона, ${{t}_{0}} = {{{{m}_{0}}x_{0}^{2}} \mathord{\left/ {\vphantom {{{{m}_{0}}x_{0}^{2}} \hbar }} \right. \kern-0em} \hbar }$ ≈ $1.57 \cdot {{10}^{{ - 23}}}$ с, ${{b}_{0}} = {{{{t}_{0}}{{\varepsilon }_{0}}} \mathord{\left/ {\vphantom {{{{t}_{0}}{{\varepsilon }_{0}}} \hbar }} \right. \kern-0em} \hbar }$ ≈ $0.02412,$ тогда в области линейной части графика зависимости пропагатора от $\tilde {\tau }$

Наличие линейной части графика зависимости (3) позволяет непосредственно вычислить квадрат модуля ненормированной волновой функции основного состояния ${{\left| {{{\Psi }_{0}}(q)} \right|}^{2}},$

а с помощью линейной регрессии найти энергию основного состояния ${{E}_{0}}$ [3, 7, 16, 17].

Формулы (1)–(5) естественным образом обобщаются на случаи большего числа степеней свободы. Поскольку волновая функция основного состояния не имеет узловых точек (линий или поверхностей) и не меняет знака, ненормированная волновая функция может быть найдена по формуле

Точность данного метода для трехмерного изотропного осциллятора с дискретным спектром состояний продемонстрирована в работе [7]. Типичные модельные парные потенциалы взаимодействия нуклонов с нуклонами, нуклонов с α-кластером и α-кластера с α-кластером имеют область притяжения с конечным радиусом и отталкивательный кор на малых расстояниях между частицами. Для проверки применимости и оценки степени точности метода для подобных потенциалов в случаях дискретного и непрерывного спектров рассмотрим модельные системы из нескольких взаимодействующих только с бесконечно тяжелым остовом частиц массы m, равной массе нейтрона. В качестве парных потенциалов выберем потенциалы, для которых известны аналитические выражения для энергии основного состояния ${{E}_{0}}.$ В модифицированном потенциале Пешля–Теллера [22], соответствующем притяжению между частицами

энергия основного состояния равна

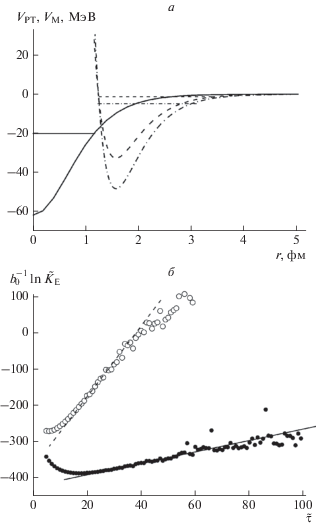
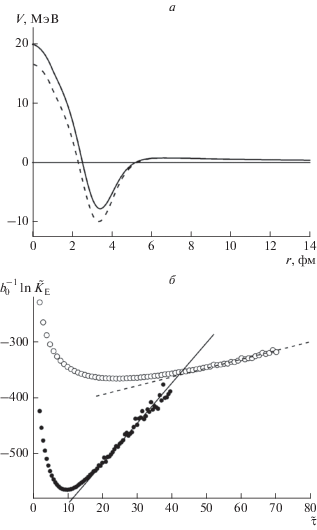
График потенциала (7), которому соответствует энергия основного состояния частицы $E_{0}^{{(1)}}$ = = −20 МэВ, показан на рис. 1а. Расчет методом Монте-Карло для $n = 2 \cdot {{10}^{6}}$ траекторий с шагом сетки $\Delta \tilde {\tau } = 0.01$ дал значение $E_{0}^{{(1)}} = 20.7 \pm 0.3$ МэВ достаточно близкое к точному.

В потенциале Морса [22] с отталкивательным кором

энергии s-состояний находятся из уравнения

где F − вырожденная гипергеометрическая функция,

Графики потенциалов (9), которым соответствуют энергии основного состояния частицы $E_{0}^{{(1)}}$ = −1 МэВ и $E_{0}^{{(1)}}$ = −5 МэВ показаны на рис. 1а. В частности, энергия равна $E_{0}^{{(1)}}$ = −1 МэВ для значений параметров $D$ = 32.82 МэВ, $\alpha $ = 3.28, ${{r}_{0}}$ = = 1.58 фм. Для системы из двух взаимодействующих только с бесконечно тяжелым остовом частиц энергия основного состояния равна $E_{0}^{{(2)}} = 2E_{0}^{{(1)}},$ для потенциалов Морса, показанных на рис. 1а, $E_{0}^{{(2)}}$ = = −2 МэВ и $E_{0}^{{(2)}}$ = −10 МэВ, соответственно. Результаты расчетов пропагатора для $n = 7 \cdot {{10}^{7}}$ траекторий с шагом сетки $\Delta \tilde {\tau } = 0.01$ показаны на рис. 1б. С помощью линейной регрессии, примененной к линейному участку графика, были получены значения $E_{0}^{{(2)}} = - 1.7 \pm 0.3$ МэВ и $E_{0}^{{(2)}} = - 10.7 \pm 0.7$ МэВ соответственно. Они достаточно хорошо согласуются с точными значениями. Недооценка точного значения −2 МэВ может быть обусловлена заметным вкладом в пропагатор состояний непрерывного спектра с ${{E}^{{(2)}}} \geqslant 0.$

ОСНОВНОЕ СОСТОЯНИЕ ЯДЕР ^6, 7Be

Принцип Паули для ядер ^{6, 7}Be можно не учитывать, если рассматривать их как систему из остова (α-кластера) и внешних нуклонов с конфигурациями {p, p} и {p, p, n} соответственно. В таком случае в рассматриваемых системах будет не более двух тождественных нуклонов. Ядерная часть потенциальной энергии взаимодействия внешних нуклонов в ядре ⁷Be может быть представлена в виде суммы парных взаимодействий нуклонов друг с другом [3, 23]

Здесь $V_{{p - n}}^{{({{1}^{ + }})}}(r)$ ‒ триплетный потенциал взаимодействия протона с нейтроном, имеющий место в дейтроне, $V_{{p - n}}^{{({{0}^{ + }})}}\left( {\left| {{{{\vec {r}}}_{1}} - {{{\vec {r}}}_{2}}} \right|} \right)$ и $V_{{p - p}}^{{({{0}^{ + }})}}\left( {\left| {{{{\vec {r}}}_{1}} - {{{\vec {r}}}_{2}}} \right|} \right)$ − это не имеющие связанных состояний синглетные потенциалы взаимодействия соответственно протона с нейтроном и протона с протоном.

Потенциал взаимодействия протона с $\alpha $-кластером ${{V}_{{p - \alpha }}}(r)$ включал ядерную (N) и кулоновскую (C) части

Для кулоновской части взаимодействия использовалось известное выражение для энергии точечного заряда в поле равномерно заряженного шара. Ядерная часть эффективного потенциала взаимодействия нуклона с ядерным остовом ${{V}_{{n - \alpha }}}(r) \equiv V_{{p - \alpha }}^{{({\text{N}})}}(r)$ в работе [3] была выбраны в виде комбинации

функций типа типа Вудса–Саксона (фермиевского распределения)

Графики функции $U(r)$ взаимодействия протона с $\alpha $-кластером в ядрах ⁶Be, ⁷Be и потенциала $V_{{p - n}}^{{({{1}^{ + }})}}$ взаимодействия протона с нейтроном в ядре ²Н показаны на рис. 2а. Выражение (15) имеет смысл псевдопотенциала сильного взаимодействия $\alpha $-кластера с нейтроном и протоном, аналогичного псевдопотенциалу [24], используемому в физике металлов для описания взаимодействия внешних электронов (из зоны проводимости) с атомными остовами. Второе положительное слагаемое в (15) объясняется наличием отталкивательных кóров в потенциалах нуклон-нуклонного взаимодействия и следствием принципа Паули. Энергия основного состояния в системе остов-нуклон оказывается близкой к энергии самого верхнего заполненного уровня оболочечной модели ядра. При этом состояния нуклонов ядерного остова, соответствующие нижележащим уровням, оказываются исключенными (запрещенными).

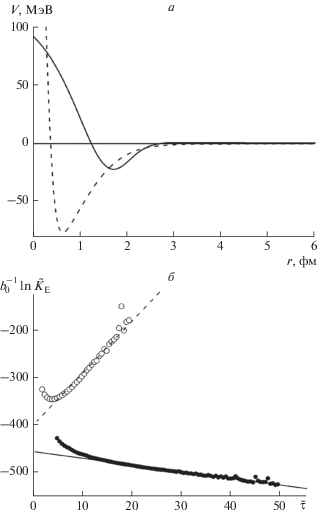
Вычисления производились в системе центра масс. Для ядра ⁶Be (системы p + p + α) с радиус-векторами протонов ${{\vec {r}}_{{{{p}_{1}}}}}{\text{,}}$ ${{\vec {r}}_{{{{p}_{2}}}}}$ и радиус-вектором α‑кластера ${{\vec {r}}_{\alpha }}$ координаты Якоби (см., например [13]) равны

Для ядра ⁷Be (системы p + p + n + α) использовались координаты Якоби

при этом из-за небольшой разницы масс протона и нейтрона их массы считались одинаковыми. Вычисление плотности вероятности по формуле (5) для ядра ⁶Be с потенциальной энергией, симметричной по отношению к перестановке протонов, дает координатную волновую функцию, симметричную по отношению к перестановке протонов. Для ядра ⁷Be с потенциальной энергией

симметричную по отношению к перестановке протонов волновую функцию можно получить, образовав симметричную комбинацию в координатах Якоби

где

Для определения энергии ${{E}_{0}}$ основного состояния ядер ^{6, 7}Be численные расчеты пропагатора (4) проводились с числом траекторий $n\sim {{10}^{6}} - {{10}^{8}}$ и шагом сетки по мнимому времени $\Delta \tilde {\tau } = 0.01.$ Результаты показаны на рис. 2. Экспериментальное значение энергии разделения ${{E}_{s}}$ ядра ⁷Be на α‑кластер, два протона и нейтрон равно 9.31 МэВ [25]. Ядро ⁶Be нестабильно, энергия системы из α‑кластера и двух протонов положительна ${{E}_{0}}$ = 0.593 МэВ [25]. Результаты расчетов пропагатора для $n = 7 \cdot {{10}^{7}}$ траекторий с шагом сетки $\Delta \tilde {\tau } = 0.01$ показаны на рис. 2б. С помощью линейной регрессии, примененной к линейному участку графика, были получены достаточно близкие к экспериментальным значения МэВ для ⁶Be и ${{E}_{0}} = - 9.{\text{5}} \pm {\text{0}}{\text{.5 }}$ МэВ для ⁷Be.

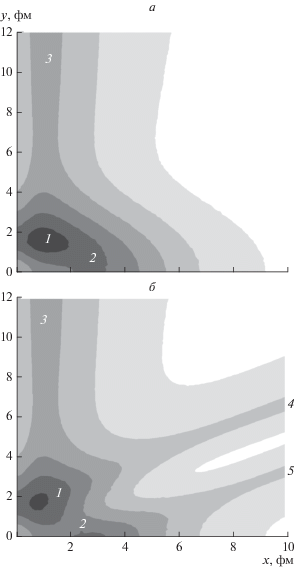
Распределение плотности вероятности ${{\tilde {K}}_{{\text{E}}}}\left( {x,y;\tilde {\tau }} \right)$ для трехтельной конфигурации короткоживущего ядра ⁶Be (p + p + α) с положительной энергией основного состояния (см. рис. 2б) показано на рис. 3. Во время существования короткоживущего ядра ⁶Ве (резонанса при тройном столкновении) наиболее вероятными являются конфигурации с объединением протонов в двухпротонный кластер и сигарообразная конфигурация (p–α–p).

Плотность вероятности ${{\left| {{{\Psi }_{0}}} \right|}^{2}}$ для четырехтельной конфигурации ядра ⁷Be (p + p + n + α) сходна с приведенной в работах [3, 4] плотностью вероятности для ядра ⁷Li (n + n + p + α). Наиболее вероятным является расположение внешних нуклонов в виде кластера ³Нe [3, 7] (правильного треугольника), тесно соединенного с почти сферическим кластером ⁴Нe. Это позволяет заключить, что ядро ⁷Be также сильно деформировано, как и сильно деформированное ядро ⁷Li с параметром квадрупольной деформации ${{\beta }_{2}} \approx - 1$ [26]. Сплюснутая форма ядра ⁷Be может соответствовать усреднению по всевозможным поворотам системы ³He + α вокруг направления, перпендикулярного межкластерной оси.

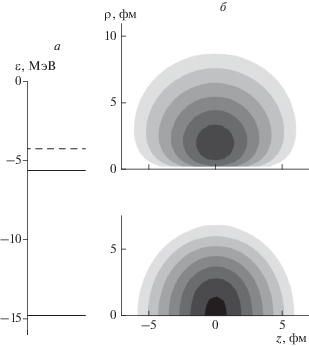
В качестве дополнительной модели ядра ⁷Be была использована оболочечная модель с аксиально-симметричной ядерной частью потенциала в форме Вудса−Саксона (см. например, [25]). Кулоновская часть потенциала для протонов представляла собой электрическое поле однородно заряженного сплюснутого эллипсоида и вычислялась численно. Численное решение уравнения Шредингера для нуклонов при ${{\beta }_{2}} = - 1$ выполнялось методом, приведенным в [27]. Значения параметров потенциала определялись из условия равенства энергий отделения нуклонов с верхних заполненных уровней экспериментальным значениям энергии отделения. Полученная схема уровней протонов (энергия отделения протона равна 5.61 МэВ, [25]) приведена на рис. 4а, плотности вероятности для заполненных низших уровней с квантовыми числами $\left| {{{m}_{j}}} \right| = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},$ $\left| {{{m}_{j}}} \right| = {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}$ ($\left| {{{m}_{j}}} \right|$ − модуль проекции полного углового момента нуклона на ось симметрии ядра) показаны на рис. 4б. Уровни и плотность вероятности для нейтронов имеют аналогичный вид. Двум нейтронам и двум протонам на глубоких низших уровнях, соответствующих уровню $1{{s}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ сферического ядра с проекцией полного момента на ось симметрии ядра $\left| {{{m}_{j}}} \right| = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},$ отвечает ядерный остов, близкий к поляризованному α-кластеру. Внешние нейтрон и два протона ядра ⁷Be на подуровне с проекцией полного момента на ось симметрии ядра $\left| {{{m}_{j}}} \right| = {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2},$ соответствующем уровню $1{{p}_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}$ сферического ядра, определяют сплюснутую форму ядра ⁷Be. Таким образом, и четырехтельная и оболочечная модели объясняют отрицательное значение параметра квадрупольной деформации ядра ⁷Be.

ОСНОВОЕ СОСТОЯНИЯ ЯДЕР ^9, 10Be

Ядра ⁹Be и ¹⁰Be представим состоящими из двух α-кластеров и из одного и двух нейтронов соответственно. Потенциальная энергия взаимодействия двух α-кластеров на расстояниях, превышающих удвоенный среднеквадратичный зарядовый радиус ядра ⁴Не (1.68 фм, см. например [25]), может быть выбрана в форме комбинации потенциала Вудса−Саксона с параметрами Акюза−Винтера [28] и потенциала кулоновского отталкивания двух точечных зарядов ${{V}_{{\alpha - \alpha }}}(r)$ = $V_{{\alpha - \alpha }}^{{({\text{N}})}}(r) + V_{{\alpha - \alpha }}^{{({\text{C}})}}(r).$ На малых расстояниях кулоновская часть $V_{{\alpha - \alpha }}^{{({\text{C}})}}(r)$ может быть представлена в форме потенциала взаимодействия двух равномерно заряженных шаров. Ядерную часть взаимодействия α-кластеров с учетом усредненного действия отталкивательного кора нуклон-нуклонного взаимодействия и принципа Паули можно описать с помощью псевдопотенциала $V_{{\alpha - \alpha }}^{{({\text{N}})}}(r)$ в форме суммы двух функций типа Вудса−Саксона

его типичные графики показаны на рис. 5а.

Для ядра ⁹Be (системы α + n + α) с радиус-векторами α-кластеров ${{\vec {r}}_{{{{\alpha }_{1}}}}}{\text{,}}$ ${{\vec {r}}_{{{{\alpha }_{2}}}}}$ и радиус-вектором нейтрона ${{\vec {r}}_{\alpha }}$ координаты Якоби равны

Для ядра ¹⁰Be (системы α + n + n + α) использовались координаты Якоби

Вычисление плотности вероятности по формуле (5) с потенциальной энергией, симметричной по отношению к перестановке α-кластеров (и нейтронов для ядра ¹⁰Be), дает координатную волновую функцию, симметричную по отношению к перестановке α-кластеров (и нейтронов для ядра ¹⁰Be).

Экспериментальные значения энергии разделения ядер ⁹Be и ¹⁰Be на α-кластеры и нейтроны равны 1.57 МэВ для ядра ⁹Be и 8.38 МэВ для ядра ¹⁰Be [25]. Результаты расчетов пропагатора для $n = 7 \cdot {{10}^{7}}$ траекторий с шагом сетки $\Delta \tilde {\tau } = 0.01$ показаны на рис. 5б. С помощью линейной регрессии, примененной к линейному участку графика, были получены близкие к экспериментальным значения ${{E}_{0}} = - {\text{1}}{\text{.57}} \pm {\text{0}}{\text{.3}}$ МэВ и ${{E}_{0}} = - {\text{8}}{\text{.3}} \pm {\text{0}}{\text{.7}}$ МэВ соответственно. Значения параметров потенциала (22) составили: ${{B}_{{\alpha 1}}}$ = 3.73 фм, ${{B}_{{\alpha 2}}}$ = 2.71 фм, ${{a}_{{\alpha 1}}}$ = =  a_α2 = 0.512 фм, U_α2 = 38 МэВ для обоих ядер, U_α1 = 27.44 МэВ для ⁹Be и U_α1 = 33 МэВ для ¹⁰Be. Небольшие различия в значениях последнего параметра можно объяснить различной поляризацией α-кластеров в ядрах ⁹Be и ¹⁰Be. Графики псевдопотенциалов (22) для ядер ⁹Be и ¹⁰Be показаны на рис. 5а, пропагаторы показаны на рис. 5б. Потенциалы взаимодействия α-кластеров с отталкивательным кором, подобные, показанным на рис. 5а рассматривались в работах [29, 30].

Распределение плотности вероятности для трехтельных конфигураций ⁹Be (α + n + α) показано на рис. 6. Наибольшую вероятность имеет конфигурация с валентным нейтроном между α‑кластерами α + n + α, конфигурация α + ⁵Не имеет меньшую вероятность. Для веса $w$ конфигурации α + ⁵Не можно использовать оценку

где $\theta $ ‒ угол между векторами $\vec {x},$ $\vec {y}{\text{,}}$

и область G – множество точек ($\vec {x},\vec {y}$), удовлетворяющих условиям $\left| {y\cos \theta } \right| > {x \mathord{\left/ {\vphantom {x 2}} \right. \kern-0em} 2}$ при $0 \leqslant x \leqslant d$ и $\left| {y\cos \theta } \right| > {x \mathord{\left/ {\vphantom {x 2}} \right. \kern-0em} 2} - c$ при $x > d.$ Для значений параметров $c = 2$ фм, $d = 5$ фм расчет дал оценку ${{w}_{{{\text{theor}}}}} \approx 0.27,$ которая согласуется с экспериментальным значением ${{w}_{{{\text{exp}}}}} \approx 0.25$ из работы [31].

Распределение плотности вероятности для четырехтельных конфигураций ¹⁰Be (α + n + n α) показано на рис. 7. Видно, что наибольшую вероятность имеет конфигурация с близко расположенными валентными нейтронами (динейтронным кластером n²) между α-кластерами (α + n²+ α), конфигурация α + ⁶Не имеет меньшую вероятность.

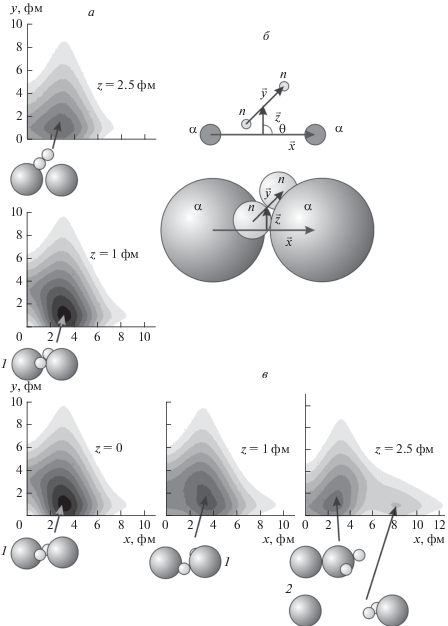
Представленные на рис. 6, 7 модели согласуются с представлениями о форме ядер ^{9, 10}Be как о ядерной молекуле [32–35], состоящей из двух α‑кластеров и внешних (валентных) нейтронов.

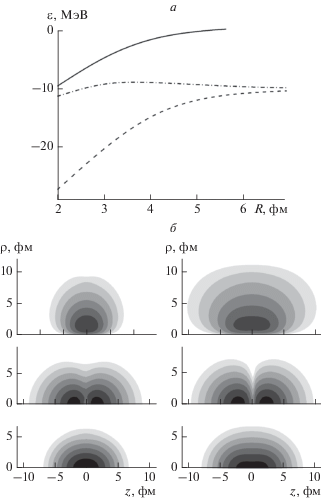
Результаты расчетов состояний нейтронов в двуцентровой оболочечной модели ядер ^9, 10Be представлены на рис. 8. Распределение плотности вероятности двух низших заполненных уровней соответствует нуклонам в двух близких видоизмененных (поляризованных) α-кластерах. Распределение плотности вероятности для третьего уровня сходно с распределениями валентных нейтронов на рис. 6, 7. Таким образом, и модель ядерной молекулы и оболочечная модель объясняют положительное значение параметра квадрупольной деформации ядер ^{9, 10}Be.

ЗАКЛЮЧЕНИЕ

Предложенный поход к расчетам характеристик основного состояния ядер ^{6, 7, 9, 10}Be может служить полезным дополнением к существующим более сложным теоретическим методам. Он позволяет достаточно просто определить зависимость энергии основного состояния от параметров потенциалов и вероятности различных конфигураций составляющих систему частиц.