Известия РАН. Серия физическая, 2020, T. 84, № 8, стр. 1167-1173

Рассеяние нейтрино в намагниченном невырожденном нуклонном газе

Рассеяние нейтрино в нуклонном газе, n + N → →  ν' + N', представляет собой простейшую актуальную проблему. Этот пример дает прозрачные и четкие результаты для сечений и скоростей передачи энергии, а также фундаментальные представления о динамике нейтрино в горячем и плотном ядерном веществе при сильных магнитных полях, вносящих заметный вклад в энергию взрыва сверхновых и достигающих десятков ТТл, см. [4‒6] и ссылки к ним. Вещество сверхновых вблизи и вне нейтрино–сферы, соответствующей сильной конвекции, при плотностях ~10¹² г · см^–3 и температуре T ~ 10 МэВ можно рассматривать как невырожденный нуклонный газ из-за сильной нейтронизации. Как следует из решения уравнения Шрёдингера для уровней энергии свободной частицы в однородном магнитном поле, сильное магнитное поле $H$ приводит к расщеплению на величину $\Delta = \left| {{{g}_{{\alpha }}}} \right|{{{\mu }}_{N}}H$ = $\left| {{{g}_{{\alpha }}}} \right|{{{\omega }}_{L}}$ энергетических уровней нуклонов со спиновыми магнитными моментами, направленными вдоль (спин вверх) и противоположно (спин вниз) относительно направления поля. Здесь ${{\mu }_{N}}$ – ядерный магнетон, а ${{g}_{{\alpha }}}$ – g-фактор нуклонов. Для рассеяния нейтрино на нуклонах, вызванного гамов-теллеровской компонентой нейтрального тока при таких условиях, из формул (1) и (2) получим следующее выражение для энергетически взвешенных интегральных значений силовой функции:

а ${{\sigma }_{{G{{T}_{0}}}}}$ – сечение рассеяния нейтрино свободными нуклонами за счет гамов-теллеровской компоненты нейтрального тока (см., например, работу [7] и ссылки в ней). В выражении (4) введены следующие обозначения: ${{\delta }_{T}} = {\Delta \mathord{\left/ {\vphantom {\Delta {2T}}} \right. \kern-0em} {2T}},$ ${{\delta }_{{\varepsilon }}} = {\Delta \mathord{\left/ {\vphantom {\Delta {{{\varepsilon }_{{\nu }}}}}} \right. \kern-0em} {{{\varepsilon }_{{\nu }}}}},$ $\theta (x)$ – ступенчатая функция Хевисайда. Таким образом, для намагниченного нуклонного газа средняя переданная энергия при неупругом рассеянии нейтрино равна $\left\langle {\Delta {{\varepsilon }_{{\nu }}}} \right\rangle $ = $\Delta {{{{\Phi }_{1}}} \mathord{\left/ {\vphantom {{{{\Phi }_{1}}} {{{\Phi }_{0}}}}} \right. \kern-0em} {{{\Phi }_{0}}}}.$ Величина $\left\langle {\Delta {{\varepsilon }_{{\nu }}}} \right\rangle $ зависит как от параметров $T,$ $\Delta $ нуклонного газа, так и от энергии ${{\varepsilon }_{\nu }}$ налетающего нейтрино.

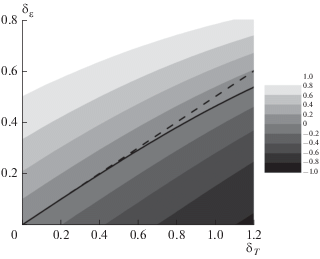
На рис. 1 для модели намагниченного нуклонного газа показана средняя переданная энергия $\left\langle {\Delta {{\varepsilon }_{{\nu }}}} \right\rangle $ в единицах $\Delta $ как функция от $\delta {}_{T}$ и ${{\delta }_{{\varepsilon }}}.$ Как видно из рисунка, средняя переданная энергия, то есть отношение ${{{{S}_{1}}} \mathord{\left/ {\vphantom {{{{S}_{1}}} {{{S}_{0}}}}} \right. \kern-0em} {{{S}_{0}}}},$ изменяется от положительного значения для горячего нуклонного газа к отрицательному для холодной системы. Такое изменение соответствует переходу от экзоэнергетического $\left( {\left\langle {\Delta {{\varepsilon }_{{\nu }}}} \right\rangle > 0} \right)$ к эндоэнергетическому $\left( {\left\langle {\Delta {{\varepsilon }_{{\nu }}}} \right\rangle < 0} \right)$ режиму рассеяния нейтрино. Переход происходит при условии ${{S}_{1}} = 0,$ т.е. при температуре $T$ = = ${{0.5\Delta } \mathord{\left/ {\vphantom {{0.5\Delta } {[ln(1 + {{\delta }_{{\varepsilon }}})}}} \right. \kern-0em} {[ln(1 + {{\delta }_{{\varepsilon }}})}}$ – $ln(1 - {{\delta }_{{\varepsilon }}})\theta (1 - {{\delta }_{{\varepsilon }}})$. Очевидно, что физической причиной такого перехода является уменьшение теплового заселения верхнего из расщепленных энергетических уровней нуклона, что ведет к подавлению вклада ГТ₀-переходов с этого уровня на нижележащий уровень. Линия перехода из одного режима в другой определяется соотношением ${{\delta }_{{\varepsilon }}}$= ${{({{e}^{{{{{\delta }}_{T}}}}} - 1)} \mathord{\left/ {\vphantom {{({{e}^{{{{{\delta }}_{T}}}}} - 1)} {(1 + {{e}^{{{{{\delta }}_{T}}}}})}}} \right. \kern-0em} {(1 + {{e}^{{{{{\delta }}_{T}}}}})}},$ и на рис.1 она показана сплошной линией. Там же пунктирной линией показана линия перехода при ${{\delta }_{T}},$ ${{\delta }_{{\varepsilon }}} \ll 1.$ В этом случае температура перехода определяется соотношением $T = {{{{\varepsilon }_{{\nu }}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{{\nu }}}} 4}} \right. \kern-0em} 4}.$ Не трудно показать, что коэффициент $1{\text{/}}4$ в этом соотношении возникает из-за степени 2 в множителе ${{({{\varepsilon }_{{\nu }}} - E)}^{2}}$ в формуле (1). Напомним, что множитель ${{({{\varepsilon }_{{\nu }}} - E)}^{2}}$ связан с объемом фазового пространства для рассеянного нейтрино.

Рис. 1.

Средняя переданная энергия $\left\langle {\Delta {{\varepsilon }_{{\nu }}}} \right\rangle $ в единицах $\Delta $при неупругом рассеянии нейтрино на намагниченном нуклонном газе. Безразмерная величина ${{\left\langle {\Delta {{\varepsilon }_{{\nu }}}} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {\Delta {{\varepsilon }_{{\nu }}}} \right\rangle } \Delta }} \right. \kern-0em} \Delta }$ показана как функция от величин ${{\delta }_{T}} = {\Delta \mathord{\left/ {\vphantom {\Delta {2T}}} \right. \kern-0em} {2T}}$ и ${{\delta }_{{\varepsilon }}} = {\Delta \mathord{\left/ {\vphantom {\Delta {{{\varepsilon }_{{\nu }}}}}} \right. \kern-0em} {{{\varepsilon }_{{\nu }}}}}.$ Темная область в правом нижнем углу соответствует отрицательным значениям ${{\left\langle {\Delta {{\varepsilon }_{{\nu }}}} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {\Delta {{\varepsilon }_{{\nu }}}} \right\rangle } \Delta }} \right. \kern-0em} \Delta }$ с минимумом равным –1, светлая область в левом верхнем углу соответствует положительной средней переданной энергии. Сплошная линия обозначает границу раздела между эндотермическим и экзотермическим режимами рассеяния, а штриховая линия соответствует соотношению ${{\varepsilon }_{{\nu }}} = 4T$ между энергией нейтрино и температурой.

Рассеяние нейтрино на нагретом ядре ⁵⁶Fe

В качестве следующего примера рассмотрим рассеяние нейтрино на нагретых ядрах, а именно на нуклиде ⁵⁶Fe – одном из наиболее распространенных ядер в веществе мантии сверхновых. Для расчета величин ${{S}_{n}}$ мы будем использовать так называемый метод теплового квазичастичного приближения случайной фазы (ТКПСФ) [9–11], который использует статистическую формулировку ядерной задачи многих тел при ненулевой температуре.

В методе ТКПСФ зависящая от температуры ${\text{Г}}{{{\text{Т}}}_{0}}$-силовая функция нагретого ядра ${{\Sigma }_{{G{{T}_{0}}}}}(E,T)$ выражается через собственные функции так называемого теплового гамильтониана $\mathcal{H} = H - \tilde {H}.$ Здесь H – гамильтониан ядра, а $\tilde {H}$ – его тильда-партнер, действующий в гильбертовом пространстве изоморфном таковому исходного гамильтониана H [12]. Тепловой гамильтониан диагонализуется в терминах тепловых мультипольных фононов

Вакуум тепловых фононов, $\left| {0(T)} \right\rangle ,$ называется тепловым вакуумом, и он описывает равновесное состояние нагретого ядра. Взаимодействие с нейтрино приводит к возбуждению одно-фононных состояний над тепловым вакуумом. ${\text{Г}}{{{\text{Т}}}_{0}}$-переходы, вызванные рассеянием нейтрино, ведут к возбуждению тепловых фононов с моментом и четностью ${{J}^{{\pi }}} = {{1}^{ + }}.$ В этом случае силовую функцию можно выразить через матричные элементы оператора $G{{T}_{0}}$ = $\sum\nolimits_k {{{{\vec {\sigma }}}^{{(k)}}}t_{0}^{{(k)}}} $ между тепловым вакуумом и одно-фононными состояниями с ${{J}^{{\pi }}} = {{1}^{ + }}{\text{:}}$

Переходы с теплового вакуума на фононы с положительной энергией описывают эндоэнергетический процесс, в котором ядро получает энергию от налетающей частицы $\left( {\Delta {{\varepsilon }_{{\nu }}} < 0} \right),$ а переходы на тильда-фононные состояния с отрицательной энергией соответствуют экзоэнергетическому процессу, когда энергию получает налетающая частица $\left( {\Delta {{\varepsilon }_{{\nu }}} > 0} \right).$ Вероятности экзо- и эндоэнергетических процессов связаны принципом детального баланса ${{\tilde {\xi }}_{k}} = {{e}^{{{{ - {{{\omega }}_{k}}} \mathord{\left/ {\vphantom {{ - {{{\omega }}_{k}}} T}} \right. \kern-0em} T}}}}{{\xi }_{k}}.$

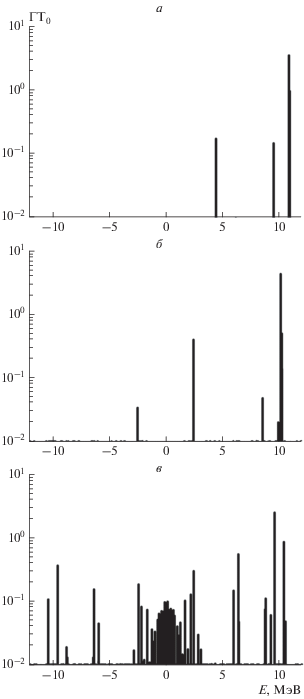
Для расчета силовой функции ГТ-переходов в нагретом ядре ⁵⁶Fe и анализа температурных эффектов, влияющих на рассеяние нейтрино мы объединили ТКПСФ с методом энергетического функционала для сил Скирма (см. работу [11] и ссылки в ней). В данной работе мы использовали силы Скирма SkM*. На рис. 2 показано, как меняется силовая функция ${\text{Г}}{{{\text{Т}}}_{0}}$-переходов с ростом температуры ядра. Для основного состояния, т.е. при $T = 0,$ практически вся сила зарядово-нейтральных ГТ-переходов концентрируется в резонансном состоянии с энергией $E \approx 10\,\,{\text{МэВ,}}$ и лишь небольшая часть силы находится при низкой энергии $E \approx 4\,\,{\text{МэВ}}{\text{.}}$ Согласно нашим расчетам, резонансное состояние является суперпозицией протонных и нейтронных квазичастичных конфигураций, возбуждающихся при одночастичном переходе с переворотом спина $1{{f}_{{{7 \mathord{\left/ {\vphantom {7 2}} \right. \kern-0em} 2}}}} \to 1{{f}_{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}.$ Низколежащее состояние формируется за счет нейтронного перехода $2{{p}_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}} \to 2{{p}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$ Так как оператор ГТ перехода не действует на угловую часть одночастичной волновой функции, то ${{1}^{ + }}$ переход $2{{p}_{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}} \to 1{{f}_{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}$ не дает вклад в распределение ${\text{Г}}{{{\text{Т}}}_{0}}$-силы.

Рис. 2.

Силовая функция зарядово-нейтральных Гамов–Теллеровских переходов в ⁵⁶Fe. Силовая функция показана для нескольких значений температуры: $T$ = 0 (а), $T$ = 1 (б) и $T$ = 5 МэВ (в).

Энергетическая щель ≈4 МэВ между основным состоянием и нижайшим 1⁺ состоянием приводит к порогу реакции неупругого рассеяния нейтрино на ⁵⁶Fe (см. рис. 3а). Отметим, что согласно экспериментальным данным нижайшее ${{1}^{ + }}$ возбужденное состояние в ⁵⁶Fe находится при энергии 3.12 МэВ [14]. При ненулевой температуре тепловое размытие нейтронной и протонной поверхностей Ферми в ядре приводит к разблокировке ${\text{Г}}{{{\text{Т}}}_{0}}$-переходов, запрещенных в основном состоянии принципом Паули. В результате происходит усиление низкоэнергетической области силовой функции. Кроме того, согласно принципу детального баланса происходит экспоненциальный рост той части силовой функции, которая находится в области отрицательных энергий, и, следовательно, дает вклад в экзоэнергетические процессы. Данный рост вызван тепловым заселением возбужденных состояний ядра и их последующим распадом. В частности, пик ${\text{Г}}{{{\text{Т}}}_{0}}$-силы при энергии $E \approx - 10\,\,{\text{МэВ}}$ соответствует девозбуждению ${\text{Г}}{{{\text{Т}}}_{0}}$-резонанса. Повышение температуры также ведет к разблокировке низкоэнергетических запрещенных переходов. Однако, как показано в [10] их вклад в процесс неупругого рассеяния нейтрино с энергией ${{\varepsilon }_{{\nu }}} \leqslant 20\,\,{\text{МэВ}}$ несущественен.

Рис. 3.

a – Сечение неупругого рассеяния нейтрино на ⁵⁶Fe как функция энергии нейтрино ${{\varepsilon }_{{\nu }}}$ при температурах $T$ = 0 (сплошная линия с квадратами), $T$ = = 1.0 МэВ (сплошная линия), $T$ = 2.0 МэВ (штриховая линия), $T$ = 3.0 МэВ (точечная линия), $T$ = = 4.0 МэВ (штриховая линия с одной точкой) и $T$ = = 5.0 МэВ (штриховая линия с двумя точками). б – Относительный вклад $\alpha $ экзотермически рассеянных нейтрино как функция температуры $T$ при энергии налетающего нейтрино ${{\varepsilon }_{{\nu }}}$ = 5 МэВ (сплошная линия), ${{\varepsilon }_{{\nu }}}$ = 10 МэВ (штриховая линия), ${{\varepsilon }_{{\nu }}}$ = 15 МэВ (штриховая линия с одной точкой), ${{\varepsilon }_{{\nu }}}$ = 20 МэВ (штриховая линия с двумя точками).

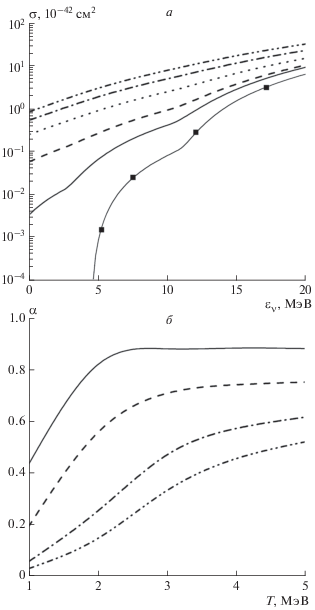
На рис. 3а показано, как меняется сечение $\sigma = {{S}_{0}}$ неупругого рассеяния нейтрино с ростом температуры ядра ⁵⁶Fe. Как видно, при $T = 0$ сечение резко возрастает при достижении нейтрино порога неупругого рассеяния ${{{\varepsilon }}_{{\nu }}} \approx 4\,\,{\text{МэВ}}{\text{.}}$ При $T \ne 0$ из-за разблокировки переходов с низкой и отрицательной энергией порог реакции исчезает, и низкоэнергетическая часть сечения возрастает более чем на три порядка при увеличении температуры от 1 до 5 МэВ. Помимо этого, как видно из рис. 3а, тепловые эффекты влияют и на высокоэнергетическую часть сечения.

Для анализа относительной роли экзо- и эндоэнергетических процессов в тепловом росте сечения рассеяния рассмотрим отношение

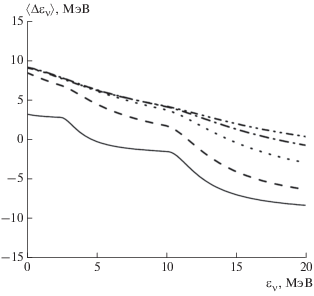
Рассмотрим теперь влияние тепловых эффектов на обмен энергией между нейтрино и нагретым ядром ⁵⁶Fe в терминах средней переданной энергии $\left\langle {\Delta {{\varepsilon }_{{\nu }}}} \right\rangle $ = ${{{{S}_{1}}} \mathord{\left/ {\vphantom {{{{S}_{1}}} {{{S}_{0}}}}} \right. \kern-0em} {{{S}_{0}}}}.$ На рис. 4 величина $\left\langle {\Delta {{\varepsilon }_{{\nu }}}} \right\rangle $ показана как функция энергии налетающего нейтрино ${{{\varepsilon }}_{{\nu }}}$ для различных значений температуры $T.$ Для средней переданной энергии при неупругом рассеянии на ⁵⁶Fe мы наблюдаем тот же самый эффект, что был обнаружен при рассмотрении рассеяния нейтрино на намагниченном нуклонном газе. А именно, для данной энергии нейтрино значение $\left\langle {\Delta {{\varepsilon }_{{\nu }}}} \right\rangle $ меняется от отрицательного к положительному при росте температуры. Из предыдущего обсуждения ясно, что изменение знака средней переданной энергии, то есть переход от эндоэнергетического рассеяния $\left( {\left\langle {\Delta {{\varepsilon }_{{\nu }}}} \right\rangle < 0} \right)$ к экзоэнергетическому $\left( {\left\langle {\Delta {{\varepsilon }_{{\nu }}}} \right\rangle > 0} \right),$ происходит вследствие усиления роли ${\text{Г}}{{{\text{Т}}}_{0}}$-переходов связанных с разрядкой возбужденных состояний ядра. При достаточно больших температурах происходит заселение ${\text{Г}}{{{\text{Т}}}_{0}}$-резонанса, и при малой энергии нейтрино его девозбуждение дает основной вклад в увеличение энергии нейтрино. В результате оказывается, что $\left\langle {\Delta {{\varepsilon }_{{\nu }}}} \right\rangle \approx 9\,\,{\text{МэВ}}{\text{.}}$ Кроме того, чем выше температура, тем выше критическая энергия нейтрино ${{\varepsilon }_{\nu }},$ при которой происходит переход от экзоэнергетического к эндоэнергетическому режиму рассеяния. Для рассматриваемых температур $T$ = 1, 2, 3, 4, 5 МэВ данный переход происходит при энергиях нейтрино ${{\varepsilon }_{{\nu }}}$ = 4.6, 11.6, 14.4, 18.1 и 20.5 МэВ соответственно.

Рис. 4.

Средняя энергия $\left\langle {\Delta {{\varepsilon }_{{\nu }}}} \right\rangle $ переданная нейтрино при неупругом рассеянии на нагретом ядре ⁵⁶Fe как функция энергии налетающего нейтрино ${{\varepsilon }_{{\nu }}}.$ Средняя переданная энергия $\left\langle {\Delta {{\varepsilon }_{{\nu }}}} \right\rangle $ показана при температурах $T$ = 1.0 МэВ (сплошная линия), $T$ = 2.0 МэВ (штриховая линия), $T$ = 3.0 МэВ (точечная линия), $T$ = = 4.0 МэВ (штриховая линия с одной точкой) и $T$ = = 5.0 МэВ (штриховая линия с двумя точками).

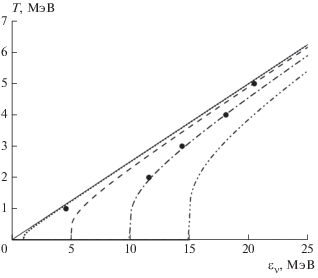
На рис. 5, для намагниченного нуклонного газа показана зависимость между температурой $T,$ при которой средняя переданная энергия обращается в ноль, и энергией налетающего нейтрино ${{\varepsilon }_{{\nu }}}.$ Как видно из рисунка, экзотермический режим осуществляется при температуре $T > {{{{\varepsilon }_{{\nu }}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{{\nu }}}} 4}} \right. \kern-0em} 4}$ или при энергии нейтрино, не превосходящей порог $\Delta $ эндоэнергетической реакции. Однако в последнем случае сечение рассеяния мало. Эндоэнергетический режим доминирует при больших энергиях нейтрино ${{\varepsilon }_{{\nu }}} > 4T,$ превосходящих порог $\Delta .$ Полученные ранее энергии нейтрино ${{{\varepsilon }}_{{\nu }}}$ = 4.6, 11.6, 14.4, 18.1 и 20.5 МэВ, при которых происходит смена режима рассеяния нейтрино на ⁵⁶Fe для температур $T$ = 1, 2, 3, 4, 5 МэВ, показаны на рис. 5 сплошными кружками. Как видно из рисунка, при энергии нейтрино превышающей энергию ГТ₀-резонанса, сплошные кружки с хорошей точностью попадают на кривую соответствующую намагниченному нуклонному газу с расщеплением между уровнями $\Delta $ = 10 МэВ. Данное обстоятельство не является удивительным, так как при энергии нейтрино больше чем энергия ГТ₀-резонанса, процесс рассеяния на ⁵⁶Fe в основном определяется возбуждением и девозбуждением ГТ₀-резонанса, энергия которого $E$ ≈ 10 МэВ.

Рис. 5.

Зависимость между энергией ${{\varepsilon }_{{\nu }}}$ нейтрино и температурой T, при которой средняя переданная энергия $\left\langle {\Delta {{\varepsilon }_{{\nu }}}} \right\rangle $ обращается в ноль. Для нуклонного газа эта зависимость показана для различных значений расщепления $\Delta $ энергетических уровней: $\Delta $ = 1 МэВ (точечная линия), $\Delta $ = 5 МэВ (штриховая линия), $\Delta $ = 10 МэВ (штриховая линия с одной точкой) и $\Delta $ = = 15 МэВ (штриховая линия с двумя точкам). Сплошная линия соответствует соотношению ${{\varepsilon }_{{\nu }}} = 4T.$ Сплошные кружки соответствуют рассеянию на ⁵⁶Fe.