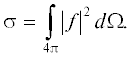Известия РАН. Серия физическая, 2020, T. 84, № 8, стр. 1205-1208

ВВЕДЕНИЕ

В предыдущих работах [1–3] были рассмотрены некоторые задачи, в которых изучалось рассеяние на объектах, не обладающих сферической симметрией. В частности, рассматривалась молекулярная дифракция [2] и рассеяние нейтронов на несферических ядрах [3]. Эти задачи сводились к решению двумерного уравнения Шредингера с аксиально симметричным потенциалом. Представляет интерес более общая проблема, когда такую симметрию использовать невозможно. Это, например, общий случай рассеяния ядерных частиц на несферических ядрах или дифракция атомных или молекулярных пучков на сложных объектах. В настоящей работе описывается численная схема решения трехмерных задач.

В качестве иллюстрации приводится пример потенциального рассеяния с аксиальной симметрией, но на более сложном объекте – пластине Френеля. Такое рассеяние интересно новыми возможностями волновой фокусировки атомных и молекулярных пучков при комнатных температурах, что уже принципиально демонстрируется на эксперименте. Так, в работах [5, 6] описан эксперимент по фокусировке пучка нейтральных частиц (атомов и молекул) с помощью микроскопической пластины Френеля. Пластина получена с помощью литографии электронным пучком (electron beam lithography), минимальный размер самой дальней зоны порядка 50 нм. Экспериментально продемонстрирована фокусировка на расстояния 15 мкм, и авторы исследования считают вполне реалистичной при современном уровне технологий фокусировку на расстояния 300 нм. В связи с выходом технологий на данный уровень представляет интерес изучение эффектов рассеяния, связанных с сложной структурой фокусируемых частиц.

Полученные результаты могут быть использованы, прежде всего, для физики наноструктур. Также исследование управления атомных и молекулярных пучков может быть полезно для связанных с нанофизикой разделов химии, медицины и атомной интерферометрии [7–11]. Схема решения также может быть применена для различных областей, в том числе, в ядерной физике – для задачи рассеяния на несферическом ядре.

МОДЕЛЬ ТРЕХМЕРНОГО РАССЕЯНИЯ

В работах [1–3] использовалось двумерное уравнение Шрёдингера для аксиально-симметричного рассеяния:

где ${{k}^{2}} = {{2mE} \mathord{\left/ {\vphantom {{2mE} {{{\hbar }^{2}}}}} \right. \kern-0em} {{{\hbar }^{2}}}}$ – волновое число, E – энергия системы, $\Psi (\vec {r})$ = $\Psi (r,\vartheta )$ – волновая функция. Размерность потенциальной энергии (константы перед потенциалом) в уравнении (1) имеет размерность квадрата волнового числа. Потенциал короткодействующий, ограничен в некоторой области: $V = 0$ при $r > {{r}_{V}}.$

Расширим задачу до более общего случая. Пусть рассматривается рассеяние в трехмерном пространстве:

где $\Delta $ – оператор Лапласа. Асимптотический вид волновой функции

определяет амплитуду рассеяния $f,$ которая подчиняется оптической теореме [12]

с полным сечением $\sigma {\text{:}}$

Соотношение (4), т.е. условие сохранения вероятности, можно использовать как критерий точности численного решения задачи.

Поскольку для (1) имеется хорошо разработанная методика решения, уравнение (2) приводится к системе уравнений типа (1). Перепишем $\Delta = {{\Delta }_{{r\vartheta }}}$ + $\frac{1}{{{{r}^{2}}{{{\sin }}^{2}}\theta }}\frac{{{{\partial }^{2}}}}{{\partial {{\varphi }^{2}}}}$ и представим волновую функцию как сумму:

Тогда (2), после действия лапласиана на азимутальную часть имеет вид

Умножая уравнение слева на ${{\left( {2\pi } \right)}^{{ - 1}}}{{e}^{{ - im{\varphi }}}}$ и интегрируя по углу $\varphi ,$ получаем систему уравнений:

где ${{V}_{{mm{\kern 1pt} '}}}$ =

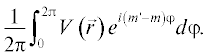
Для решения системы уравнений используются алгоритмы, описанные ранее [1–3], с некоторой модификацией. Так, при $r > {{r}_{V}},$ справедливо свободное решение уравнений (1), (2), которое удобно уже представить в виде разложения по присоединенным функциям Лежандра $P_{l}^{m}\left( {\cos \vartheta } \right){\text{:}}$

с неизвестными коэффициентами a_lm. Здесь $h_{l}^{{\left( 1 \right)}}\left( {kr} \right)$ – сферическая функция Бесселя третьего рода. Функция (5) имеет асимптотический вид (3) с амплитудой:

которая выражается через коэффициенты ${{a}_{{lm}}}.$ Заметим, что из (6) следует независимость амплитуды от угла $\varphi $ при $\vartheta = 0$ и возможность использования оптической теоремы в форме (4).

Практически поиск неизвестных коэффициентов ${{a}_{{lm}}}$ реализуется следующим образом. После приведения уравнения (2) к дискретному виду, используется метод матричной прогонки [13], который базируется на линейной связи ${{\Psi }_{{j - 1}}} = {{Z}_{j}}{{\Psi }_{j}} + {{D}_{j}}$ для любой точки ${{r}_{j}}.$ Матричная запись дискретизированного уравнения с учетом граничного условия при $r = 0$ позволяет рекуррентным образом определить матрицы ${{Z}_{j}}$ и ${{D}_{j}}$ для любого ${{r}_{j}}.$ На границе $r = {{r}_{{sh}}} > {{r}_{V}}$ записывается уравнение для неизвестных коэффициентов ${{a}_{{lm}}},$ для чего используется функция $\Psi \left( {\vec {r}} \right)$ в виде разложения (5).

Предельное значение по орбитальному моменту может быть оценено из квазиклассического соотношения ${{l}_{{max}}}k\sim R,$ где $R$ – характерный размер области взаимодействия. Предельное значение m определяется из соотношения $\left| m \right| \leqslant l,$ однако, в реальных задачах с достаточно гладкими потенциалами и возникающей из-за этого сходимостью ${{V}_{{m{\kern 1pt} 'm}}}$ при сильно отличных индексах вполне допустимо ограничиться меньшими значениями этого числа. В наших расчетах мы использовали квазиклассическую оценку для поиска ${{l}_{{max}}},$ ${{m}_{{max}}},$ минимизирующую ошибку выполнения условия (4). Проектируя слева полученное уравнение на $P_{{l{\kern 1pt} '}}^{m},$ получаем набор линейных уравнений. Решение этой системы уравнений дает искомые коэффициенты.

В результате становится известной не только амплитуда (6), но и волновая функция в любой точке пространства, где допустимо свободное решение $\left( {r > {{r}_{V}}} \right).$

Для проверки алгоритма был проведён расчет задачи рассеяния на сферически симметричном потенциале – прямоугольной яме. Сравнение показало надeжную работу в области предполагаемых размеров объектов рассеяния и предполагаемых энергий. Также критерием точности служит условие выполнения оптической теоремы (4) при расчетах.

РАСЧЕТЫ УПРУГОГО РАССЕЯНИЯ НА ПЛАСТИНКЕ ФРЕНЕЛЯ

Для демонстрации возможностей описанного выше алгоритма численного решения задачи трехмерного рассеяния (2) предварительно была изучена проблема аксиально-симметричного рассеяния атомных и молекулярных пучков на сложной наноструктуре – пластинке Френеля. Для расчета была использована модель пластинки с тремя кольцами, рассчитанная для волны микрочастиц с ${{k}^{2}}$ = = 10⁴ нм^–2. Таким частицам соответствует длина волны де Бройля $\lambda \approx 0.0628$ нм.

Потенциал взаимодействия одной точечной частицы (атома) с пластинкой Френеля записывается в сферических координатах в виде:

где пространство $\Omega $ описывает пластинку Френеля, в цилиндрических координатах $\rho = r\sin \vartheta ,$ $z = r\cos \vartheta $ оно записывается $\left| z \right| \leqslant {{{{z}_{d}}} \mathord{\left/ {\vphantom {{{{z}_{d}}} 2}} \right. \kern-0em} 2},$ $\rho \in \left[ {{{\rho }_{{1n}}},{{\rho }_{{2n}}}} \right],$ $n = 1,2,3.$ Толщина пластинки ${{z}_{d}}$ была выбрана равной 0.02 нм, размер колец пластинки были рассчитаны из задачи фокусировки пучка атомов как волн с известной длиной волны $\lambda $ на фокусном расстоянии ${{d}_{f}} = $ 1 нм:

Параметр высоты потенциала был выбран ${{V}_{0}} \approx 3 \cdot {{10}^{6}}$ нм⁻², для легкой молекулы в данной работе это значение точно соответствует 4000 К, (${{{{V}_{0}}} \mathord{\left/ {\vphantom {{{{V}_{0}}} {{{k}_{B}}}}} \right. \kern-0em} {{{k}_{B}}}}$ = 4000 К, ${{k}_{B}}$ – постоянная Больцмана) т.е. потенциал практически непрозрачен для атомов и молекул при комнатных температурах.

Прохождение такой пластинки пучком двухатомных гомоядерных молекул можно описать в приближении жесткой молекулы в широкой области энергий [1, 4]. В этом случае используется потенциал вида

где $d$ – размер молекулы (межатомное расстояние). Данное одномерное приближение позволяет учесть характеристики резонансного прохождения барьера связанной частицей. В данной работе параметр $d$ был выбран достаточно большим, ~0.25 нм. Большое межатомное расстояние обеспечивает в задачах резонансной диффузии более яркие резонансные эффекты [1, 2, 4].

На рис. 1 приведен трехмерный вид квадрата модуля волновой функции вида (5) с вычисленными коэффициентами ${{a}_{{l0}}}$ для пучка атомов с ${{k}^{2}}$ = = 10⁴ нм^–2 (что соответствует 75 K). На рис. 2 приведены несколько линейных разрезов графика квадрата модуля волновой функции в цилиндрических координатах $\rho ,$ $z.$ Видно, что вдоль оси z при $\rho = 0$ находится ярко выраженный максимум волновой функции в районе $z$ ∼ 1 нм. Таким образом, качественно воспроизводятся результаты эксперимента [5, 6], конечно, на существенно упрощенной модели.

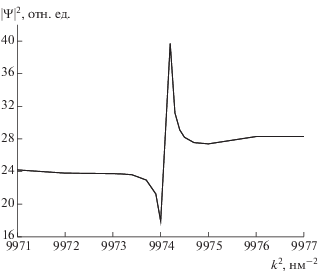
Упругое рассеяние двухатомных молекул также сопровождается эффектом фокусировки. Общий вид квадрата волновой функции подобен приведенному на рис. 1, 2. Однако, рассеяние молекул имеет одну интересную особенность. Если рассеяние пучка атомов на малом интервале по энергии практически не изменяется, то рассеяние молекул имеет существенно немонотонную зависимость. На рис. 3 приведена зависимость максимального значения квадрата модуля волновой функции в районе $z\sim 1\,\,{\text{нм,}}$ $\rho = 0$ (стрелка на рис. 2) от квадрата волнового числа для прохождения пучка двухатомных молекул. Явно видна сложная, резонансная зависимость изменения высоты. Это соответствует общей картине дифракции молекул на дисках и отверстиях [4]. Вместе с тем, здесь наблюдается более сложная картина, так как возможно не только изменение высоты, но также миграция положения максимума по оси $z$ и даже возникновение максимумов более сложной формы (двух-, трехгорбых и т.д.). Характерной особенностью является узость резонансных явлений, приблизительные ширины предполагаемых резонансов около десятых долей единиц задачи. Вместе с этим необходимо отметить, что описание столь узких резонансов приводит к необходимости использовать более аккуратные численные методы. Подробное изучение этого эффекта может дать новые интересные возможности применения в области интерферометрии, управления пучков и связанных областях знаний.

ЗАКЛЮЧЕНИЕ

В работе предложен алгоритм решения трехмерных уравнений Шрёдингера. Разработан метод решения задач рассеяния в трехмерном пространстве для потенциалов, не сохраняющих момент импульса.

Найдены волновые функции для рассеяния атомов и двухатомных гомоядерных молекул на сложной структуре – пластинке Френеля. Показано, что возможен эффект фокусировки атомов и молекул.

Показано существование резонансных эффектов для фокусировки молекул. В частности, резонансное увеличение значения квадрата модуля волновой функции и соответственно уменьшение области фокусировки от энергии налетающих молекул.

Работа выполнена при финансовой поддержке гранта полномочного представителя Республики Казахстан в ОИЯИ № 434 2018 г. Часть численных расчетов производилась на кластере HYBRILIT ОИЯИ (hybrilit.jinr.ru).