1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 84, № 9, 2020

Известия РАН. Серия физическая, 2020, T. 84, № 9, стр. 1367-1369

Частотное управление емкостью и проводимостью диэлектрика при релаксационной поляризации

А. С. Богатин 1, *, А. Л. Буланова 1, С. А. Ковригина 1, И. О. Носачев 1

1 Федеральное государственное автономное образовательное учреждение высшего образования “Южный федеральный университет”, Научно-исследовательский институт физики
Ростов-на-Дону, Россия

* E-mail: asbbogatin@sfedu.ru

Поступила в редакцию 19.03.2020
После доработки 10.04.2020
Принята к публикации 27.05.2020

Полный текст (PDF)

Аннотация

Установлены взаимные зависимости между параметрами традиционного описания релаксационной поляризации в веществе с помощью уравнения Дебая и параметрами импедансных способов описания. В рамках модели двухслойного конденсатора с утечкой установлены закономерности переходов к сильному релаксационному процессу, исчезновения максимумов в частотных зависимостях тангеса угла диэлектрических потерь, мнимых частей емкости диэлектрика как функций отношений сопротивлений и емкостей слоев диэлектрика. Проанализированы возможности частотного управления проводимостью и емкостью гетерогенных диэлектриков. При отрицательной емкости одного из слоев найдена возможность существенного увеличения модуля отрицательной емкости гетерогенного диэлектрика.

Наиболее простым способом релаксационная поляризация описывается в случае, когда диэлектрические спектры можно представить с помощью распределения Дебая. Эта ситуация реализуется релаксаторами, имеющими одинаковое время срабатывания (релаксации) τ. Эмпирическая формула, подобранная Дебаем для описания диэлектрических спектров, обусловленных дипольно-ориентационной поляризацией [1] (1), была обоснована в [2] термодинамическими методами, где показано, что распределением можно пользоваться и при многих других поляризационных моделях. Достаточно только, чтобы процесс затухал экспоненциально и выполнялся принцип суперпозиции поляризационных токов.

(1)
$~{\varepsilon }{\kern 1pt} {\text{*}} = {{{\varepsilon }}_{\infty }} + {{{\Delta \varepsilon }} \mathord{\left/ {\vphantom {{{\Delta \varepsilon }} {\left( {1 + i{\omega \tau }} \right)}}} \right. \kern-0em} {\left( {1 + i{\omega \tau }} \right)}},$
где Δε = εst – ε∞– вклад релаксационного процесса в диэлектрическую проницаемость вещества, разность между статическим и высокочастотным значениями диэлектрической проницаемости, ω – круговая частота электрического поля. Формула Дебая не учитывает развития в веществе сквозной электропроводности. Учесть ее оказывается удобным при описании процессов электропереноса в веществе методами импедансной спектроскопии [3–5]. Импедансная спектроскопия предполагает постановку в соответствие описываем процессам электропереноса эквивалентных электрических схем. Для дебаевского процесса поляризации, дополненного сквозной электропроводностью, эквивалентная схема имеет вид, приведенный на рис. 1а. В ней емкость С3 описывает быстрые поляризационные процессы, проводимость G3 (1/R3) – сквозную электропроводность, последовательная R4–C4 цепочка – собственно релаксационный процесс. Адмитанс $G_{{\text{1}}}^{*}$ для образца вещества, которому поставлена в соответствие эта эквивалентная схема, имеет вид (2).
(2)
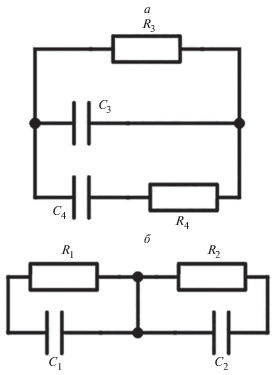
$\begin{gathered} G_{1}^{*} = {{G}_{3}}(1 + {{{\omega }}^{2}}(\tau _{4}^{4} + {{C}_{4}}{{R}_{3}}{{{\tau }}_{4}}) + \\ + \,\,i{\omega }{{{\text{(}}{{C}_{4}}{{R}_{3}} + {{{\tau }}_{3}} + {{{\omega }}^{2}}{{{\tau }}_{3}}{\tau }_{4}^{2}))} \mathord{\left/ {\vphantom {{{\text{(}}{{C}_{4}}{{R}_{3}} + {{{\tau }}_{3}} + {{{\omega }}^{2}}{{{\tau }}_{3}}{\tau }_{4}^{2}))} {(1 + {{{\omega }}^{2}}{\tau }_{4}^{2})}}} \right. \kern-0em} {(1 + {{{\omega }}^{2}}{\tau }_{4}^{2})}}; \\ \end{gathered} $
где τ4 = R4C4; τ3 = С3/G3.

Рис. 1.

Эквивалентные электрические схемы диэлектриков с дебаевской релаксационной поляризацией.

Параметры распределения Дебая, использованные в (1) связаны с параметрами эквивалентной схемы 1 а соотношениями (3).

(3)
${\tau } = {{{\tau }}_{4}};\,\,{\Delta \varepsilon } = {{{{С}_{4}}} \mathord{\left/ {\vphantom {{{{С}_{4}}} {\left( {{{{\varepsilon }}_{0}}K} \right)}}} \right. \kern-0em} {\left( {{{{\varepsilon }}_{0}}K} \right)}};~\,\,{{\varepsilon }_{\infty }} = {{{{С}_{3}}} \mathord{\left/ {\vphantom {{{{С}_{3}}} {\left( {{{{\varepsilon }}_{0}}K} \right)}}} \right. \kern-0em} {\left( {{{{\varepsilon }}_{0}}K} \right)}}.$

Здесь ε0 – электрическая постоянная, а K – множитель, зависящий от геометрии образца вещества. Одним из видов дебаевской релаксационной поляризации является междуслойная поляризация. Ее наиболее простая эквивалентная схема – два последовательно включенных конденсатора с утечкой (рис. 1б). Адмиттанс такого электрического соединения имеет вид (4).

(4)
$\begin{gathered} G_{2}^{*} = ({{R}_{1}} + {{R}_{2}} + {{{\omega }}^{2}}({\tau }_{1}^{2}{{R}_{2}} + {\tau }_{2}^{2}{{R}_{1}}) + \\ + \,\,\,i{\omega (}{{{\tau }}_{1}}{{R}_{1}} + {{{\tau }}_{2}}{{R}_{2}} + \\ + \,\,{{{\omega }}^{2}}{{({{{\tau }}_{1}}{\tau }_{2}^{2}{{R}_{1}} + {\tau }_{1}^{2}{{{\tau }}_{2}}{{R}_{2}})))} \mathord{\left/ {\vphantom {{({{{\tau }}_{1}}{\tau }_{2}^{2}{{R}_{1}} + {\tau }_{1}^{2}{{{\tau }}_{2}}{{R}_{2}})))} {({{{({{R}_{1}} + {{R}_{2}})}}^{2}}}}} \right. \kern-0em} {({{{({{R}_{1}} + {{R}_{2}})}}^{2}}}} + \\ + \,\,{{\omega }^{2}}{{{\text{(}}{{{\tau }}_{2}}{{R}_{1}} + {{{\tau }}_{1}}{{R}_{2}})}^{2}}), \\ \end{gathered} $
где τ1 = R1C1; τ2 = R2C2.

Взаимосвязь параметров используемых эквивалентных электрических схем описывается соотношениями (5)

(5)
$\begin{gathered} {{R}_{3}} = {{R}_{1}} + {{R}_{2}};\,\,\,{{C}_{3}} = \frac{{\left( {{{С}_{1}}{{С}_{2}}} \right)}}{{\left( {{{С}_{1}} + {{С}_{2}}} \right)}};~ \\ {{R}_{4}} = {{(\left( {{{R}_{1}} + {{R}_{2}}} \right){{R}_{1}}{{R}_{2}}{{{({{C}_{!}} + {{C}_{2}})}}^{2}})} \mathord{\left/ {\vphantom {{(\left( {{{R}_{1}} + {{R}_{2}}} \right){{R}_{1}}{{R}_{2}}{{{({{C}_{!}} + {{C}_{2}})}}^{2}})} {({{{({{R}_{1}}{{C}_{1}} - {{R}_{2}}{{C}_{2}})}}^{2}}}}} \right. \kern-0em} {({{{({{R}_{1}}{{C}_{1}} - {{R}_{2}}{{C}_{2}})}}^{2}}}};~ \\ {{C}_{4}} = {{{{{({{C}_{1}}{{R}_{1}} - {{C}_{2}}{{R}_{2}})}}^{2}}} \mathord{\left/ {\vphantom {{{{{({{C}_{1}}{{R}_{1}} - {{C}_{2}}{{R}_{2}})}}^{2}}} {({{{({{R}_{1}} + {{R}_{2}})}}^{2}}({{C}_{1}} + {{C}_{2}}))}}} \right. \kern-0em} {({{{({{R}_{1}} + {{R}_{2}})}}^{2}}({{C}_{1}} + {{C}_{2}}))}}. \\ \end{gathered} $

Пользуясь представлениями о гетерогенном образце вещества, можно оценить границы перехода к сильным релаксационным поляризациям [6, 7] как

(6)
${{c}^{2}}{{r}^{2}} - 18cr - 8{\text{c}}{{r}^{2}} - 8c + 1 = 0.$

Исчезновение максимумов в частотных зависимостях мнимых частей диэлектрической проницаемости описывается уравнением

(7)
${{c}^{2}}{{r}^{2}} - 18cr - 8r{{c}^{2}} - 8r + 1 = 0{\text{\;}}{\text{.}}$

Исчезновения максимумов в частотных зависимостях тангенса угла диэлектрических потерь при слабых релаксационных поляризациях уравнением

(8)
$\begin{gathered} \frac{{8rc\left( {r + 1} \right)\left( {c + 1} \right)}}{{{{{(rc - 1)}}^{2}}}} - \frac{{r\left( {c + 1} \right)}}{{r + 1}} - \\ - \,\,\frac{{c\left( {r + 1} \right)}}{{c + 1}} - \frac{{{{c}^{2}}{{r}^{2}} - 2cr + 1}}{{\left( {r + 1} \right)\left( {c + 1} \right)}} = 0; \\ \end{gathered} $

В соотношениях (6)–(8) использованы обозначения c = C1/C2; r = R1/R2.

Проводимость и емкость образца гетерогенного диэлектрика описывается соотношениями (9) и (10) соответственно

(9)
$\begin{gathered} G = {{({{R}_{1}} + {{R}_{2}} + {{{\omega }}^{2}}({\tau }_{1}^{2}{{R}_{2}} + {\tau }_{2}^{2}{{R}_{1}}))} \mathord{\left/ {\vphantom {{({{R}_{1}} + {{R}_{2}} + {{{\omega }}^{2}}({\tau }_{1}^{2}{{R}_{2}} + {\tau }_{2}^{2}{{R}_{1}}))} {({{{({{R}_{1}} + {{R}_{2}})}}^{2}}}}} \right. \kern-0em} {({{{({{R}_{1}} + {{R}_{2}})}}^{2}}}} + \\ + \,\,{{{\omega }}^{2}}{{({{{\tau }}_{2}}{{R}_{1}} + {{{\tau }}_{1}}{{R}_{2}})}^{2}}), \\ \end{gathered} $;
(10)
$\begin{gathered} C = ({{{\tau }}_{1}}{{R}_{1}} + {{{\tau }}_{2}}{{R}_{2}} + \\ + \,\,{{{\omega }}^{2}}{{\left( {{{{\tau }}_{1}}{{{\tau }}_{2}}\left( {{{{\tau }}_{2}}{{R}_{1}} + {{{\tau }}_{1}}{{R}_{2}}} \right)} \right)} \mathord{\left/ {\vphantom {{\left( {{{{\tau }}_{1}}{{{\tau }}_{2}}\left( {{{{\tau }}_{2}}{{R}_{1}} + {{{\tau }}_{1}}{{R}_{2}}} \right)} \right)} {({{{({{R}_{1}} + {{R}_{2}})}}^{2}}}}} \right. \kern-0em} {({{{({{R}_{1}} + {{R}_{2}})}}^{2}}}} + \\ + \,\,{{{\omega }}^{2}}{{({{{\tau }}_{2}}{{R}_{1}} + {{{\tau }}_{1}}{{R}_{2}})}^{2}}). \\ \end{gathered} $

Таким образом, открывается возможность частотного управления проводимостью и емкостью гетерогенных диэлектриков.

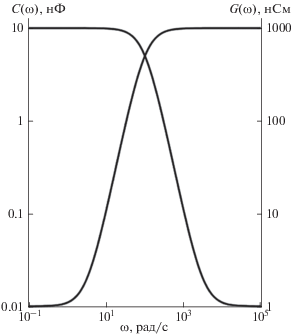
В ряде работ [8–10] обсуждаются возможности гигантского увеличения проводимости G и емкости C гетерогенных диэлектриков. В [11] проанализированы возможности управления скоростью частотного изменения G и С для двухслойных диэлектриков. При этом определены величины с и r, при которых возможен одновременный гигантский рост G и С или гигантский рост одной из этих величин, сопровождаемый медленным изменением второй. Пример гигантского частотного изменения G и С приведен на рис. 2.

Рис. 2.

Частотные зависимости емкости С и проводимости G дебаевского двухслойного диэлектрика. R1 = = 106; R2 = 109 Ом; τ1 = 10–5; τ2 = 10 с.

Последнее время появилось большое количество публикаций, связанных с обнаружением отрицательной диэлектрической проницаемости в веществе [12–14]. Среди веществ с отрицательной емкостью имеются гетерогенные вещества [15]. В случае, когда один из слоев двуслойного диэлектрика имеет отрицательную емкость общая емкость С такого диэлектрика имеет вид (11), где (–С2 < 0)

(11)
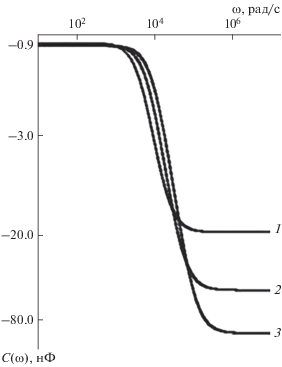
$\begin{gathered} C = ({{C}_{1}}R_{1}^{2} - {{C}_{2}}R_{2}^{2} + \\ + \,\,{{{\omega }}^{2}}{{\left( {{{C}_{1}}{{C}_{2}}R_{1}^{2}R_{2}^{2}\left( {{{C}_{1}} - {{C}_{2}}} \right)} \right)} \mathord{\left/ {\vphantom {{\left( {{{C}_{1}}{{C}_{2}}R_{1}^{2}R_{2}^{2}\left( {{{C}_{1}} - {{C}_{2}}} \right)} \right)} {({{{({{R}_{1}} + {{R}_{2}})}}^{2}}}}} \right. \kern-0em} {({{{({{R}_{1}} + {{R}_{2}})}}^{2}}}} + \\ + \,\,{{{\omega }}^{2}}{{({{C}_{1}} - {{C}_{2}})}^{2}}R_{1}^{2}R_{2}^{2}). \\ \end{gathered} $

Анализ вражения (11) позволяет увидеть, что и вэтом случае возможно частотное управление емкостью гетерогенного образца. Причем, и это самый интересный факт, модуль отрицательной емкости диэлектрика за счет подбора c и r может быть увеличен в десятки и сотни раз. Это хорошо видно на рис. 3, где представлены частотные зависимости емкостей двуслойного диэлектрика, один из слоев которого характеризуется отрицательной емкостью.

Рис. 3.

Частотые зависимости емкости двухслойного диэлектрика, один из слоев которого имеет отрицательную емкость (–С2 < 0). R1 = 106 Ом; R2 = 2 ⋅ 107 Ом; C1 = 10 нФ; (1) С2 = 9.5; (2) С2 = 9.8; (3) С2 = 9.9 нФ.

Список литературы

  1. Дебай П. Полярные молекулы. М.-Л.: ГНТИ, 1931. 247 с.

  2. Smyth C.P. Dielectric behavior and structure. McGraw-Hill, 1955. 441 p.

  3. E.Barsoukov, J.R.Macdonald. Impedance spectroscopy theory, experiment, and applications. John Wiley & Sons, 2005. 608 p.

  4. Челидзе Т.Л., Деревянко А.И., Куркленко О.Д. Электрическая спектроскопия гетерогенных систем. Киев: Наукова думка, 1977. 232 с.

  5. Богатин А.С., Андреев Е.В., Ковригина С.А., Богатина В.Н. // Изв. РАН. Сер. физ. 2014. Т. 78. № 4. С. 483; Bogatin A.S., Andreev E.V., Kovrigina S.A., Bogatina V.N. // Bull. Russ. Acad. Sci. Phys. 2014. V. 78. № 4. P. 317.

  6. Турик А.В., Богатин А.С., Андреев Е.В. // ФТТ. 2011. Т. 53. № 12. С. 2299.

  7. Богатин А.С., Турик А.В., Ковригина С.А, Андреев Е.В. // Изв. РАН. Сер. физ. 2010. Т. 74. № 9. С. 1266; Bogatin A.S., Andreev E.V., Kovrigina S.A., Bogatina V.N. // Bull. Russ. Acad. Sci. Phys. 2010. V. 74. № 9. P. 1212.

  8. Lemonov V.V., Sotnicova E.P., Weihnacht M. // ФTT. 2002. T. 44. № 11. C. 1948.

  9. Diu J., Duan C.-G., Yin W.-G. et al. // Phys. Rev. B. 2004. V. 70. Art. № 144105.

  10. Турик А.В., Радченко Г.С., Чернобабов А.Н. и др. // ФТТ. 2006. Т. 48. № 6. С. 1088.

  11. Куропаткина С.А., Раевский И.П., Богатин А.С. // Изв. РАН. Сер. физ. 2007. Т. 71. № 2. С. 238; Kuropatkina S.A., Raevskii I.P., Bogatin A.S. // Bull. Russ. Acad. Sci. Phys. 2007. V. 71. № 2. P. 228.

  12. Jonscher A.K. // J. Chem. Soc. Faraday Trans. 1986. V. 82. P. 75.

  13. Болтаев А.П., Пудонин Ф.А. // Кр. сообщ по физ. ФИАН. 2011. № 7. С. 3.

  14. Shulman J., Xue Y.Y., Tsui S. et al. // Phys. Rev. B. 2009. V.80. Art. № 134202.

  15. Богатин А.С., Буланова А.Л., Андреев Е.В. и др. // Изв. РАН. Сер. физ. 2018. Т. 82. № 7. С. 892; Bogatin A.S., Bulanova A.L., Andreev E.V. et al. // Bull. Russ. Acad. Sci. Phys. 2018. V. 82. № 7. P. 800.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал