1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 85, № 1, 2021

Известия РАН. Серия физическая, 2021, T. 85, № 1, стр. 52-58

Верификация моделей микрополя по спектрам плотной лазерной плазмы

А. А. Белов 1, 2, *, Н. Н. Калиткин 3

1 Федеральное государственное бюджетное образовательное учреждение высшего образования “Московский государственный университет имени М.В. Ломоносова”, физический факультет
Москва, Россия

2 Федеральное государственное автономное образовательное учреждение высшего образования “Российский университет дружбы народов”
Москва, Россия

3 Федеральное государственное бюджетное учреждение науки Институт прикладной математики имени М.В. Келдыша Российской академии наук
Москва, Россия

* E-mail: aa.belov@physics.msu.ru

Поступила в редакцию 20.07.2020
После доработки 28.08.2020
Принята к публикации 28.09.2020

Полный текст (PDF)

Аннотация

Оптические свойства плотной плазмы сильно зависят от внутриплазменных электрических полей (так называемое микрополе). Дан критический обзор существующих теоретических моделей плазменного микрополя. Проведена верификация важнейших моделей по экспериментам, в которых плотная плазма создавалась мощным лазерным излучением. Показано, что наилучшее теоретическое обоснование и наилучшее согласие с экспериментами имеет модель квазинезависимых частиц QUIP.

ВВЕДЕНИЕ

Плотная плазма используется в очень многих технических и экспериментальных конструкциях: сильноточные электрические разряды, мощные газоразрядные лазеры, магнитокумулятивные генераторы, термоядерные мишени и т.д. Расчет таких конструкций требует знания оптических свойств плазмы. На эти свойства сильно влияет так называемое микрополе – это электрическое поле внутри плазмы, порожденное хаотическим тепловым движением ионов и свободных электронов. Это поле флуктуирует во времени и пространстве.

До сих пор для кулоновских систем не найдено математически строгих методов исследования. Существуют лишь более или менее удачные модели. Уже 100 лет предпринимаются попытки построить такие модели для количественного описания свойств микрополя.

В данной работе приведен критический анализ существующих моделей микрополя и показано, что почти все они неправильно описывают “хвосты” функции распределения и не могут предсказать количество экспериментально наблюдаемых спектральных линий.

Ранее авторами была предложена модель QUIP (QUasi-Independent Particles), полученная из первых принципов. Эта модель правильно описывает “хвосты” функции распределения и даже пространственную неоднородность микрополя. Проведена апробация модели путем сравнения с экспериментами по спектрам излучения сверхплотной лазерной плазмы.

Отмечено, что сравнение следует проводить по числу наблюдаемых линий в спектральных сериях, поскольку именно это число сильно зависит от принятой модели. Выбраны эксперименты, наиболее подходящие для такой проверки. Это эксперименты по свечению плазмы Al или Ar, в которых видны лаймановские серии водородо- и гелиеподобных ионов. Показано, что модель QUIP описывает эти эксперименты лучше, чем другие известные модели.

МОДЕЛИ МИКРОПОЛЯ

Подробный обзор существующих моделей микрополя представлен в работе [1]. Поэтому мы не будем подробно описывать сами известные модели и ограничимся только их критическим разбором.

Метод Фурье-образа

Изучение микрополя начал Хольцмарк [2]. Он использовал интегральное преобразование Фурье. Поскольку для кулоновских систем точных методов не разработано, Хольцмарк строил Фурье-образ на основе модельных соображений, и по этому приближенному Фурье-образу обратным интегральным преобразованием Фурье восстанавливал функцию распределения. Она получалась в виде интеграла, не берущегося в элементарных функциях. Распределение Хольцмарка приведено на рис. 1, где для напряженности E выбран характерный масштаб ${{\left\langle Z \right\rangle } \mathord{\left/ {\vphantom {{\left\langle Z \right\rangle } {{{R}^{2}}}}} \right. \kern-0em} {{{R}^{2}}}};$ здесь $\left\langle Z \right\rangle $ – усредненный заряд всех сортов частиц, R – радиус сферизованной атомной ячейки. Напомним, что распределение Хольцмарка соответствует пространственно однородному микрополю.

Рис. 1.

Функции распределения однородного микрополя; 1 – модель Хольцмарка, 2 – модель SHO, 3 – модель QUIP.

В последующие годы было опубликовано много работ по усовершенствованию модели Хольцмарка. В подавляющем большинстве из них также использовался интеграл Фурье, но с другими приближениями при построении Фурье-образа. Перечислим эти модели, отсылая за подробностями к оригинальным работам или обзору [2].

В модели Эккера и Мюллера [3, 4] вместо кулоновского потенциала использовался дебаевский. Беренгер и Мозер [5, 6] использовали цепочку уравнений Боголюбова, дебаевский потенциал и метод кластерного разложения. Хупер [7–9] развивал сходные подходы, но радиус дебаевской экранировки использовал как подгоночный параметр. Иглесиас усложнил модель Хупера, вводя факторы с дополнительными свободными параметрами, подгоняемыми под экспериментальные данные [10–13]. Модели такого же типа развивал Голосной [14, 15]. Неоднородность микрополя в рамках того же круга идей учитывалась в работах Чандрасекара и фон Ноймана [16–18], Кудрина [19], Шолина [20], Демуры [21–28].

Напомним, что перечисленные выше работы основаны на интегральном преобразовании Фурье. Однако в 1960-е годы Тихонов и его ученики показали [29], что интегральное преобразование Фурье является некорректной математической операцией. Это проявляется в том, что незначительное искажение Фурье-образа может привести к большим искажениям распределения, восстановленного обратным преобразованием Фурье. Поэтому результат оказывается сильно чувствительным к модельным предположениям, использованным при построении Фурье-образа. Покажем, что все описанные модели действительно приводят к серьезному физическому дефекту.

В самом деле, у всех этих моделей распределение $p(E)$ при $E \to \infty $ имеет медленно убывающую асимптотику $p(E)\sim {{E}^{{{{ - 5} \mathord{\left/ {\vphantom {{ - 5} 2}} \right. \kern-0em} 2}}}}$ [1]. Но электрическое поле напряженности E имеет плотность энергии ${{{{E}^{2}}} \mathord{\left/ {\vphantom {{{{E}^{2}}} {(8\pi )}}} \right. \kern-0em} {(8\pi )}}.$

Поэтому усредненная по распределению плотность энергии

(1)
$\frac{1}{{8\pi }}\int\limits_0^\infty {{{E}^{2}}p(E)dE} $
оказывается бесконечной: интеграл расходится на верхнем пределе! Поскольку физически энергия поля и вообще любые моменты от функции распределения не могут быть бесконечными, это указывает на неадекватность степенного хвоста функции распределения. Данное противоречие не отмечено в мировой литературе. Поэтому указанными распределениями можно пользоваться лишь в районе максимума $p(E)$ и для тех задач, в которых “хвосты” распределения несущественны.

В лазерной плазме типичные условия таковы, что основной вклад в ширину линии дает именно микрополе. Оценки показывают, что в экспериментах (см., например, [30–32]) доплеровское уширение составляет ~1 эВ. В то же время грубая оценка микрополевого уширения дает 15–20 эВ, что по порядку величины согласуется с экспериментом.

Отсюда следует, что асимптотика распределения $p(E)$ важна еще по одной причине: она отвечает за крылья спектральных линий. Ширина крыльев линии играет важную роль при вычислении росселандова среднего от пробега фотонов. А эта средняя величина является характеристикой прозрачности плазмы для излучения. Именно росселандово среднее отвечает, например, за характерное время транспортировки энергии от ядра звезды к поверхности.

Если “хвост” распределения затухает медленно, то крылья линий должны быть широкими. Однако в эксперименте этого не наблюдается: крылья затухают очень быстро. На это же указывает сравнение [33] экспериментов с теориями в работах [34–37]. В них, в частности, отмечено, что расчет прозрачности плазмы не согласуется с экспериментальным данными.

Несколько особняком стоят другие методы, упомянутые в обзоре [1]. Рассмотрим их.

Метод коллективных координат

На основе метода коллективных координат [38, 39] была построена модель простых гармонических осцилляторов (SHO) [40, 41]. Эта модель выводилась для плотной горячей плазмы (например, внутри звезд). В ней функция распределения гауссова, так что плотность энергии является конечной. Это распределение приведено на рис. 1.

При применении этой модели возникают следующие трудности. Во-первых, положение максимума распределения сильно зависит от T и быстро сдвигается в сторону больших полей при уменьшении T. В то же время в большинстве других моделей положение максимума зависит от T слабо или не зависит вовсе. Аналогично, при T модель SHO также расходится с экспериментом и не согласуется с другими моделями.

По-видимому, для модели SHO должна существовать какая-то граница применимости по температуре и плотности. Однако в публикациях мы не нашли такого ограничения.

Во-вторых, при описании различных свойств плазмы важно обеспечить самосогласованность и непротиворечивость. Иначе в расчетах возможно появление нефизичных артефактов. В частности, чтобы обеспечить непротиворечивость термодинамики и оптики, нужно учитывать энергию микрополя в термодинамическом потенциале свободной энергии. Это слагаемое можно рассматривать как поправку на неидеальность для модели Саха. Однако такая поправка на основе модели SHO быстро убывает при уменьшении температуры (то есть увеличении неидеальности плазмы) [42]. Это также не согласуется с другими моделями.

Кроме того, модель SHO основана на использовании пробного заряда. Положить его равным нулю нельзя, иначе масштаб микрополя оказывается бесконечным. Поэтому модель SHO не может описать микрополе в нейтральной точке. Это также является недостатком модели SHO.

Метод функционала плотности

Делались попытки применять к проблеме микрополя метод функционала плотности [43‒52]. Этот метод считают построенным из первых принципов. Его основой является теорема Кона и Хёнберга о том, что существует некоторый функционал от электронной плотности, который достигает своего минимального значения, если в него подставить точную электронную плотность основного состояния. Однако неизвестно, как найти данный функционал. Поэтому на практике вместо функционала от электронной плотности используют функционал от комбинации одноэлектронных волновых функций. Для такого функционала указанная теорема не имеет силы. Вдобавок, в модель обычно вводят подгоночные параметры. Поэтому метод фактически перестает быть первопринципным. В результате распределения микрополя, построенные в работах [43, 44], имеют степенные асимптотики [1], т.е. также приводят к бесконечной плотности энергии поля. Поэтому к методу функционала плотности следует относиться с осторожностью.

Метод Монте-Карло

Первопринципными являются методы Монте-Карло, в том числе, методы молекулярной динамики [53–61]. По ним выполняют расчеты, которые используют для апробации описанных выше моделей. Однако практическая реализация этих методов имеет ряд слабых мест.

Во-первых, используется число частиц ~1000. Они занимают объем ~10 межатомных расстояний. Влияние частиц за пределами указанного объема учитывают с помощью некоторых граничных условий (чаще всего периодических). Для незаряженных частиц с быстро убывающим потенциалом взаимодействия это может быть удовлетворительным. Но для дальнодействующего кулоновского взаимодействия чувствительность результатов к выбору граничных условий оказывается большой.

Во-вторых, электроны имеют гораздо меньшую массу и гораздо большие скорости, чем ионы. Поэтому для расчета их динамики приходится выбирать очень малый шаг интегрирования по времени. Сама система дифференциальных уравнений динамики является плохо обусловленной, то есть фактически некорректной [29]. Результат вычислений сильно зависит от начальных положений и скоростей частиц. При этом, чем дольше ведется расчет, тем сильнее сказывается этот эффект.

Поэтому функция распределения вычисляется с невысокой точностью. Ее можно удовлетворительно определить в районе максимума, но практически невозможно найти асимптотики, на которые следует обращать особое внимание.

Пробный заряд

Во многих моделях (например, модели SHO, APEX и ряд других) вводится в рассмотрение пробный заряд ${{Z}_{0}},$ расположенный в точке наблюдения. В этом случае другие заряды уже не могут быть распределены равномерно в пространстве и должны удовлетворять распределению Больцмана. Это исключает сколь угодно сильные сближения ионов. Вклад ионов в микрополе в Z раз больше, чем вклад электронов. Поэтому учет больцмановской статистики для ионов уменьшает вероятность больших микрополей. Например, введение пробного заряда в модели SHO делает функцию распределения микрополя гауссовой и обеспечивает конечность всех моментов распределения. Этот вывод подтверждается расчетами методом Монте-Карло [62]. Поэтому представляется трудно объяснимым, что в моделях типа APEX, использующих пробный заряд, асимптотика функции распределения все равно убывает только по степенному закону.

Для электронов нужно учитывать квантовый эффект – дебройлевскую длину волны электрона. Поэтому электроны могут сближаться с ионами лишь на расстояния порядка дебройлевской длины волны. Это также уменьшает вероятность больших микрополей.

Таким образом, учет неоднородности распределения зарядов по пространству является физически адекватным. Введение пробного заряда – это простейший способ учесть такую неоднородность.

Однако этот способ имеет недостаток. Для оптических приложений нужно знать микрополе в окрестности именно иона, то есть тяжелой частицы. Этот заряд находится в хаотическом тепловом движении, причем его скорость примерно такова же, как у других тяжелых частиц. Поэтому пренебрегать его движением нельзя. Соответственно, система отсчета, связанная с таким зарядом, является неинерциальной. Введение неинерциальной системы координат крайне усложнило бы модель и затруднило получение простой реализации. В существующих моделях подобные системы координат не вводятся.

Кроме того, положение границ атомной ячейки определяется мгновенным положением зарядов. Поэтому при движении пробного заряда постоянно менялись бы границы его атомной ячейки. Это также сильно усложнило бы модель.

Таким образом, неясно, как можно корректно сформулировать модель пробного заряда.

Критика известных моделей

Подводя итог анализу известных моделей, сформулируем их основные недостатки.

Во-первых, самый важный недостаток большинства известных моделей – бесконечный второй момент функции распределения (то есть объемная плотность энергии микрополя). Это столь же нефизично, как нарушение закона сохранения энергии.

Во-вторых, медленное затухание “хвоста” функции распределения приводит к появлению широких крыльев у спектральных линий, от которых сильно зависит оптическая прозрачность плазмы. В эксперименте, напротив, крылья линий настолько быстро затухают, что практически незаметны. В ряде работ модели микрополя верифицируются с помощью описания контуров линии. Однако при этом описывается не весь контур, а только центральная часть линии. Кроме того, такая интерпретация крайне сложна, так как она зависит от температуры и плотности мишеней, которые экспериментально не измеряются. Более подробный разбор этого будет сделан в разделе, посвященном описанию экспериментов.

Точность определения температуры и плотности плазмы по ее спектру сильно зависит от принятой модели микрополя. В существующих методах анализа спектров проводят индивидуальную подгонку каждой линии в спектральной серии. При этом описание каждой линии производится с помощью своей температуры и плотности, и эти температуры и плотности для разных линий между собой не согласуются. Подробнее этот вопрос будет рассмотрен в разделе, посвященном описанию экспериментов.

В-третьих, далее показано, что существующие методы диагностики не согласуются с расчетами ионного состава и, следовательно, с термодинамикой плазмы. Это еще один принципиальный дефект существующих моделей.

Модель QUIP

Перечисленные недостатки удается преодолеть в модели QUIP – Quasi-Independent Particles. Для однородного микрополя этот подход был предложен Калиткиным и Козлитиным [63–65] (эти работы не рассматривались в обзоре [1]). В этом подходе использовался первый принцип – закон больших чисел. Из него следует, что компоненты напряженности микрополя имеют гауссово распределение, а длина вектора напряженности микрополя – максвелловское распределение. Распределение модуля вектора напряженности однородного микрополя приведено на рис. 1. Положение максимума близко к таковому у распределения Хольцмарка. Однако функция распределения при $E \to \infty $ убывает не по степенному закону, а по экспоненциальному, то есть несоизмеримо быстрее. Поэтому все моменты указанных распределений, включая плотность энергии поля, становятся конечными.

Отметим, что в модели QUIP все формулы расчета распределений очень просты, так что она удобна для использования. Все остальные современные модели требуют громоздких численных расчетов, и только авторы этих моделей фактически могут ими пользоваться. Последнее отмечалось в обзоре [1].

ВЕРИФИКАЦИЯ МОДЕЛЕЙ

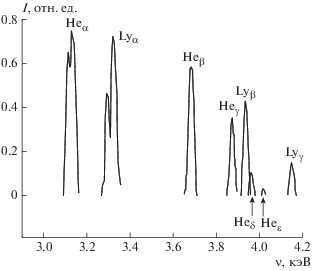
Спектры излучения сверхплотной лазерной плазмы получены в уникальных экспериментах [30–32] и ряде других. Они позволяют провести верификацию моделей микрополя. Наиболее представителен эксперимент [31] с плазмой Ar + + Kr 50/50. Полученный спектр приведен на рис. 2. На нем видны 3 линии лаймановской серии водородоподобного иона Ar+17 и вся лаймановская серия гелиеподобного иона Ar+16. В последней серии интенсивность пятой линии мала, а последующие линии незаметны. Расчет показал, что серия Ar+16 светит при температуре $T\sim 400$ эВ, $\rho \sim 0.2$ г/см3.

Рис. 2.

Спектр Ar+16 в эксперименте [31].

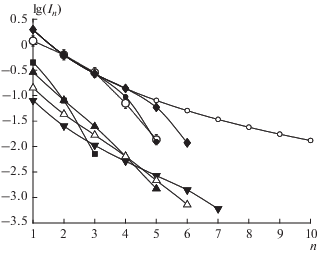
На рис. 3 показаны относительные интенсивности различных линий этой серии как экспериментальные (площади контуров линий на рис. 2), так и рассчитанные по разным моделям в водородоподобном приближении.

Рис. 3.

Относительные интенсивности линий спектра Ar+16; пунктир – эксперимент [31]; сплошные линии – модели: ⚫ – QUIP, ◆ – SHO, ◼ – Хольцмарк, ▼ – модель [68], ▲ – модель [11], △ – модели [12, 67], ⚪ – расчет без учета микрополя.

Ни одна модель не может описать интенсивность α-линии гелиеподобного иона Ar+16, поскольку к ней не применимо водородоподобное приближение. Для остальных линий серии оно применимо достаточно хорошо. Но эта причина не имеет отношения к моделям микрополя.

В эксперименте наблюдается 5 линий. Модель QUIP правильно описывает наблюдаемое число линий и интенсивности линий $\beta {\text{--}}\varepsilon .$ По модели SHO должны наблюдаться 6 линий. В модели Хольцмарка видны только 3 линии.

Разные варианты модели APEX не согласуются между собой. Расчет по модели Хупера [67] практически совпадает с вариантом модели APEX [12], поэтому обе модели показаны одной кривой. Эти модели предсказывают на одну линию больше, чем в эксперименте. Модель [68] предсказывает значительно большее число линий, чем наблюдается в эксперименте. Модель [11] предсказывает правильное число наблюдаемых линий, однако интенсивность линий γ и δ несколько слабее по сравнению с интенсивностью β-линии, чем в эксперименте. Таким образом, наилучшее согласие с экспериментом обеспечивает модель QUIP.

Исследование выполнено при поддержке Российского научного фонда (проект № 16-11-10001).

Список литературы

  1. Demura A.V. // Int. J. Spectrosc. 2010. V. 2010. Art. ID 671073.

  2. Holtsmark J. // Ann. Phys. 1919. V. 58. P. 577.

  3. Ecker G. // Z. Phys. 1957. V. 148. No 5. P. 593.

  4. Ecker G., Muller K.G. // Z. Phys. 1958. V. 153. No 3. P. 317.

  5. Baranger M., Mozer B. // Phys. Rev. 1959. V. 115. No 3. P. 521.

  6. Mozer B., Baranger M. // Phys. Rev. 1960. V. 118. No 3. P. 626.

  7. Hooper C.F., Lineberger W.C., Bacon F.M. // Phys. Rev. 1966. V. 141. No 1. P. 165.

  8. Hooper C.F. Jr. // Phys. Rev. 1968. V. 165. No 1. P. 215.

  9. Hooper C.F. Jr. // Phys. Rev. 1968. V. 169. No 1. P. 193.

  10. Iglesias C.A., Lebowitz J.L., MacGowan D. // Phys. Rev. A. 1983. V. 28. No 3. P. 1667.

  11. Iglesias C.A., DeWitt H.E., Lebowitz J.T. et al. // Phys. Rev. A. 1985. V. 31. P. 1698.

  12. Dufty J.W., Boercker D.B., Iglesias C.A. // Phys. Rev. A. 1985. V. 31. No 3. P. 1681.

  13. Iglesias C.A., Rogers F.J., Shepherd R. et al. // J. Quant. Spectrosc. Radiat. Transf. 2000. V. 65. No 1–3. P. 303.

  14. Голосной И.О. // Мат. моделир. 1991. Т. 3. № 9. С. 49.

  15. Голосной И.О. // Мат. моделир. 1992. Т. 4. № 6. С. 3.

  16. Chandrasekhar S., von Neuman J. // Astrophys. J. 1942. V. 95. P. 489.

  17. Chandrasekhar S., von Neuman J. // Astrophys. J. 1943. V. 97. P. 1.

  18. Chandrasekhar S. // Rev. Mod. Phys. 1943. V. 15. No 1. P. 1.

  19. Кудрин Л.П., Шолин Г.В. // Докл. АН СССР. 1962. Т. 147. С. 342.

  20. Шолин Г.В. // Опт. и спектроск. 1969. Т. 26. № 4. P. 489; Sholin G.V. // Opt. Spectrosc. USSR. 1969. V. 26. P. 275.

  21. Demura A.V., Sholin G.V. // J. Quant. Spectrosc. Radiat. Transf. 1975. V. 15. P. 881.

  22. Демура А.В. Некоторые вопросы теории уширения спектральных линий водорода в плазме. Дис. … канд. физ.-мат. наук. Москва: Институт атомной энергии им. И.В. Курчатова, 1976. 176 с.

  23. Демура А.В., Плешаков В.В., Шолин Г.В. Атлас детальных штарковских профилей спектральных линий водорода в плотной плазме. Препринт IAE-5349/6. М.: НИЦ “Курчатовский институт”, 1991. 97 с.

  24. Demura A.V., Stehle C. // AIP Conf. Proc. 1995. V. 328. P. 177.

  25. Demura A.V., Gilles D., Stehle C. // J. Quant. Spectrosc. Radiat. Transf. 1995. V. 54. P. 123.

  26. Demura A.V., Helbig V., Nikolic D. // AIP Conf. Proc. 2002. V. 645. P. 318.

  27. Djurovic S., Nikolic D., Savic I. et al. // Phys. Rev. E. 2005. V. 71. Art. No 036407.

  28. Demura A.V., Demchenko G.V., Nikolic D. // Eur. Phys. J. D. 2008. V. 46. P. 111.

  29. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 1979. 285 с.

  30. Kilkenny J.D., Lee R.W., Key M.H. et al. // Phys. Rev. A. 1980. V. 22. No 6. Art. No 2746.

  31. Hooper C.F., Jr., Mancini R.C., Kilcrease D.P. et al. // SPIE. High Inten. Laser-Matter Interact. 1988. V. 913. P. 129.

  32. Burris-Mog T.J., Mancini R.C., Bailey J.E. et al. // J. Quant. Spectrosc. Radiat. Transf. 2006. V. 99. P. 120.

  33. Perry T.S., Heeter R.F., Opachich Y.P. et al. // HEDP. 2020. V. 35. Art. No 100728.

  34. Bailey J.E., Rochau G.A., Iglesias C.A. et al. // Phys. Rev. Lett. 2007. V. 99. Art. No 265002.

  35. Bailey J.E., Nagayama T., Loisel G.P. et al. // Nature. 2015. V. 517. P. 56.

  36. Heeter R.F., Bailey J.E., Craxton R.S. et al. // J. Plasma Phys. 2017. V. 83. Art. No 595830103.

  37. Perry T.S., Heeter R.F., Opachich Y.P. et al. // High Energ. Dens. Phys. 2017. V. 23. P. 223.

  38. Bohm D., Pines D. // Phys. Rev. 1952. V. 85. P. 338.

  39. Bohm D., Pines D. // Phys. Rev. 1953. V. 92. No 3. P. 609.

  40. Broyles A.A. // Phys. Rev. 1955. V. 100. No 4. P. 1181.

  41. Broyles A.A. // Z. Phys. 1958. V. 151. P. 187.

  42. Kalitkin N.N., Lutskiy K.I. // Math. Models Comput. Simul. 2015. V. 7. P. 518.

  43. Dharma-Wardana M.W.C., Perrot F. // Phys. Rev. A. 1986. V. 33. No 5. P. 3303.

  44. Perrot F., Dharma-Wardana M.W.C. // Phys. Rev. A. 1991. V. 41. No 6. P. 3281.

  45. Hohenberg P., Kohn W. // Phys. Rev. B. 1964. V. 136. No 3. Art. No B864.

  46. Kohn W., Sham L.J. // Phys. Rev. A. 1965. V. 140. No 4. Art. No A1133.

  47. Perrot F., Dharma-Wardana M.W.C. // Phys. Rev. A. 1984. V. 30. No 5. P. 2619.

  48. Perrot F., Dharma-Wardana M.W.C. // Phys. Rev. A. 1085. V. 31. No 2. P. 970.

  49. Chihara J. // Phys. Rev. A. 1991. V. 44. No 2. Art. No 1247.

  50. Massacrier G. // J. Quant. Spectros. Radiat. Transf. 1994. V. 51. No 1–2. P. 221.

  51. Singh R., Deb B.M. // Phys. Rep. 1999. V. 311. No 2. P. 47.

  52. Kohn W. // Rev. Mod. Phys. 1999. V. 71. No 5. P. 1253.

  53. Gilles D., Angelie A. // Ann. Phys. Paris. 1986. V. 11. No 3. P. 157.

  54. Caillol J.M., Gilles D. // J. Stat. Phys. 2000. V. 100. No 5–6. P. 933.

  55. Gilles D. Calcul de la repartition statistique du microchamp electrique dans les plasmas. Internal CEA-Report, 1997.

  56. Gilles D. Methode de Monte-Carlo en mecanique statistique appliquee a la physique des plasmas. Lecture Notes. Orsay: Universite Paris XI, 1997.

  57. Potekhin A.Y., Chabrier G., Gilles D. // Phys. Rev. E. 2002. V. 65. No 3. Art. No 036412.

  58. Brush S.G., Sahlin H.L., Teller E. // J. Chem. Phys. 1966. V. 45. No 6. P. 2102.

  59. Замалин В.М., Норман Г.Э., Филинов В.С. Метод Монте-Карло в статистической термодинамике. М.: Наука, 1977.

  60. Acioli P.H. // J. Mol. Struct. 1997. V. 394. No 2–3. P. 75.

  61. Камилов И.К., Муртазаев А.К., Алиев Х.К. // УФН. 1999. Т. 169. № 7. С. 795.

  62. Kozlitin I.A. // Math. Mod Comput. Simul. 2011. V. 3. P. 58.

  63. Калиткин Н.Н., Козлитин И.А. // ДАН. 2006. Т. 411. № 1. С. 36, Kalitkin N.N., Kozlitin I.A. // Dokl. Phys. 2006. V. 51. No 11. P. 579.

  64. Калиткин Н.Н., Козлитин И.А. // ДАН. 2008. Т. 418. № 5. С. 614, Kalitkin N.N., Kozlitin I.A. // Dokl. Phys. 2008. V. 53. No 2. P. 61.

  65. Kalitkin N.N. Kozlitin I.A. // Plasma Phys. Rep. 2011. V. 37. P. 191.

  66. Kalitkin N.N., Kozlitin I.A. // Ann. Phys. 2018. V. 396. P. 468.

  67. Tighe R., Hooper C.J. // J. Phys. Rev. A. 1977. V. 15. P. 1773.

  68. Iglesias C.A., Lebowitz J. // J. Phys. Rev. A. 1984. V. 30. P. 2001.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал