Известия РАН. Серия физическая, 2021, T. 85, № 1, стр. 6-13

ВВЕДЕНИЕ

С 80-х годов прошлого столетия особое внимание уделяется распространению электромагнитных волн на границах раздела сред, в частности, металлов и диэлектриков, в связи с широкими перспективами применения композитных материалов в микро- и наноустройствах фотонной и плазмонной техники [1–6]. Высокочастотное электромагнитное поле вызывает осцилляции как свободных, так и связанных зарядов в диэлектрических, полупроводниковых средах и металлах. При этом, в результате осцилляций зарядов излучаются вторичные электромагнитные волны, которые гибридизируются с волнами поляризации связанных и свободных зарядов в среде и распространяются в объеме среды, а также вдоль границы раздела сред в форме плазмон-поляритонных волн.

Спектр плазмонов в объемном образце отличается от спектра плазмонов в тонком или толстом слоях одного и того же металла, в наночастице и в нанопроводе [1–6]. Геометрические размеры и форма объекта влияют на его резонансные свойства, радиационные эффекты и поглощение электромагнитного поля. Помимо этого, свойства поверхностных плазмон-поляритонов (ППП) зависят от параметров диэлектрической среды, с которой контактирует поверхность металла. Возбуждение ППП может осуществляться с помощью призм [1], микрозондами и микрообъективами с большой апертурой [3], с помощью спазеров [6, 7] или полупроводниковых квантовых точек [8, 9].

Внешнее электромагнитное поле действует на электроны, вызывая линейный отклик диэлектрической проницаемости металла. При увеличении амплитуды внешнего поля появляются ангармонические колебания электронов и ионов, межзонные переходы, которые приводят к проявлению нелинейных поляризационных механизмов [1]. На границе раздела сред металл-диэлектрик происходит скачок диэлектрической проницаемости, т.е. нарушение трансляционной симметрии, что обуславливает возникновение больших поверхностных токов в скин-слое. Это приводит к возникновению нелинейных поверхностных эффектов на границе раздела сред. Линейные и нелинейные эффекты при генерации и распространении объемных и поверхностных плазмон-поляритонов описываются классическими и квантовыми линейными и нелинейными моделями [10–12]. Квантовые модели позволяют выявить физические механизмы, влияющие на динамику плазмон-поляритонов в объеме среды и на границе раздела сред, исследовать нелинейные процессы.

Интенсивная электромагнитная волна или мощный электромагнитный импульс генерируют нелинейные плазмон-поляритонные волны – кноидальные волны, кинки и солитоны в объеме проводящей среды [5, 7, 11–16], и на границе раздела проводящей и диэлектрической сред [1–7, 17–22]. Свойства и динамика кноидальных волн и солитонов зависят от параметров возбуждающих электромагнитных волн и импульсов, а также от геометрии системы и свойств среды, в которой возбуждаются плазмон-поляритоны. Основная цель данной работы – исследование линейных и нелинейных процессов при распространении ППП на плоской границе раздела металла и диэлектрической среды в зависимости от граничных условий и плотности энергии электромагнитной волны, возбуждающей ППП.

МОДЫ ПОВЕРХНОСТНЫХ ПЛАЗМОН-ПОЛЯРИТОНОВ

ППП генерируются при падении электромагнитной волны на границу раздела диэлектрической и проводящей среды (металла) (рис. 1), и возникают в результате взаимодействия фотонов, фононов и плазмонов.

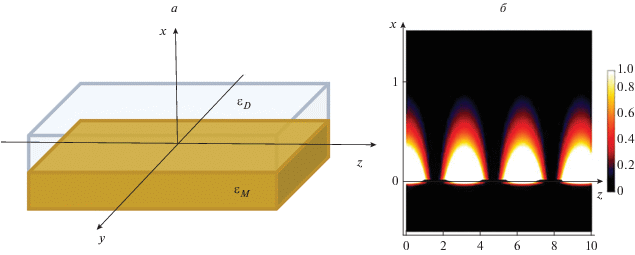
Амплитуды ППП экспоненциально убывают при удалении от границы раздела сред, т.е. ППП локализованы вблизи границы (рис. 1б). Такие волны “привязаны” к границе раздела сред и не излучаются с гладкой границы. Для трансформации поверхностной волны в объемную (излучаемую) волну гладкость границы должна быть нарушена, например, с помощью выступов, бороздок, и т.п. [1–3].

Рассмотрим механизм возникновения ППП на границе раздела однородных сред с различными диэлектрическими ${{{\varepsilon }}_{D}}$ и ${{{\varepsilon }}_{M}},$ а также магнитными ${{{\mu }}_{D}}$ и ${{{\mu }}_{M}}$ проницаемостями. В линейном режиме диэлектрические и магнитные проницаемости обеих сред не зависят от плотности энергии ППП. Полагаем, что ППП возбуждаются монохроматическим полем $\sim {\kern 1pt} \exp ( - i{\omega }t).$ Поверхностная волна распространяется вдоль границы раздела сред по оси z, а ось x направлена по нормали к границе. Поле ППП экспоненциально спадает при удалении от границы $\sim {\kern 1pt} \exp ( - {{{\alpha }}_{D}}x)$ как в положительном направлении оси $x > 0,$ так и $\sim {\kern 1pt} \exp ({{{\alpha }}_{M}}x)$ в отрицательном направлении оси $x < 0,$ причем $Re{{{\alpha }}_{D}} > 0,$ $Re{{{\alpha }}_{M}} > 0$ [1–5].

Для ППП с плоским волновым фронтом вдоль оси $y$ поле не меняется ${\partial \mathord{\left/ {\vphantom {\partial {\partial y}}} \right. \kern-0em} {\partial y}} \to 0.$ Из уравнений Максвелла $\nabla \times \vec {H} = - i{{c}^{{ - 1}}}{\omega \varepsilon }\vec {E},$ $\nabla \times \vec {E} = i{{c}^{{ - 1}}}{\omega \mu }\vec {H}$ получаем две системы уравнений для мод ППП [1]: для поперечной магнитной (ТМ-моды) с компонентами ${{H}_{y}},$ ${{E}_{x}},$ ${{E}_{z}}$ магнитного и электрического полей

и для поперечной электрической (ТЕ-моды) с компонентами ${{E}_{y}},$ ${{H}_{x}},$ ${{H}_{z}},$

Из систем уравнений (1) и (2) можно получить уравнение второго порядка для поля ${{H}_{y}}$ ТМ-моды и поля ${{E}_{y}}$ ТЕ-моды, соответственно,

Граничные условия при $x = 0$ для ТМ-моды имеют вид ${{H}_{{y1}}} = {{H}_{{y2}}},$ ${{E}_{{z1}}} = {{E}_{{z2}}},$ откуда следует $\frac{1}{{{{{\varepsilon }}_{D}}}}\frac{{d{{H}_{{Dy}}}}}{{dx}}$ = $\frac{1}{{{{{\varepsilon }}_{M}}}}\frac{{d{{H}_{{My}}}}}{{dx}},$ т.е. $ - {{{\varepsilon }}_{M}}{{{\alpha }}_{D}}$ = ${{{\varepsilon }}_{D}}{{{\alpha }}_{M}};$ для ТЕ-моды граничные условия ${{E}_{{yD}}} = {{E}_{{yM}}},$ ${{H}_{{zD}}} = {{H}_{{zM}}}$ дают равенство $\frac{1}{{{{{\mu }}_{D}}}}\frac{{d{{E}_{{Dy}}}}}{{dx}}$ = $\frac{1}{{{{\mu }_{M}}}}\frac{{d{{E}_{{My}}}}}{{dx}},$ т.е. $ - {{\mu }_{M}}{{\alpha }_{D}}$ = ${{\mu }_{D}}{{\alpha }_{M}}.$ Из граничных условий следует, что ТМ-мода ППП возбуждается на границе раздела сред с разными по знаку диэлектрическими проницаемостями, а ТЕ-мода ППП возбуждается при разных по знаку магнитных проницаемостях. В общем случае магнитная проницаемость – положительная величина, т.е. поверхностная TE-мода на границе раздела металла и диэлектрика не возбуждается. Однако в средах с отрицательной магнитной проницаемостью ТЕ-мода может быть возбуждена, так как ее магнитная проницаемость может быть отрицательной. Примером таких сред являются фотонные кристаллы и метаматериалы [23].

Решения уравнений (1)–(3) можно представить в форме ${{E}_{j}} = {{E}_{{0j}}}\exp (i{\beta }z),$ ${{H}_{j}} = {{H}_{{0j}}}\exp (i{\beta }z),$ где $j = D,M.$ Тогда остальные компоненты приобретают вид для ТМ-моды ${{E}_{x}} = \frac{{c{\beta }}}{{{\omega \varepsilon }}}{{H}_{y}},$ ${{E}_{z}} = i\frac{{c{\alpha }}}{{{\omega \varepsilon }}}{{H}_{y}},$ и для ТЕ-моды ${{H}_{x}} = - \frac{{с{\beta }}}{{{\omega \mu }}}{{E}_{y}},$ ${{H}_{z}} = - i\frac{{с{\alpha }}}{{{\omega \mu }}}{{E}_{y}}.$

Подставляя решения для ${{E}_{j}}$ и ${{H}_{j}}$ в уравнения (3), получаем характеристические уравнения для ТМ-моды и ТЕ-моды ППП ${{{\varepsilon }}_{j}}{{{\mu }}_{j}}{{c}^{{ - 2}}}{{{\omega }}^{2}}$ – ${{{\beta }}^{2}} + {\alpha }_{j}^{2} = 0,$ из этих уравнений находим коэффициенты ${{{\alpha }}_{j}}$ мод ${{{\alpha }}_{j}} = {{\left( {{{{\beta }}^{2}} - {{{\varepsilon }}_{j}}{{{\mu }}_{j}}{{c}^{{ - 2}}}{{{\omega }}^{2}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$ Исключая коэффициенты ${{{\alpha }}_{j}}$ из граничные условий $ - {{{\varepsilon }}_{M}}{{{\alpha }}_{D}} = {{{\varepsilon }}_{D}}{{{\alpha }}_{M}}$ и $ - {{{\mu }}_{M}}{{{\alpha }}_{D}} = {{{\mu }}_{D}}{{{\alpha }}_{M}},$ получаем дисперсионные уравнения для ТМ-моды ${{{\omega }}^{2}} - \frac{{{\varepsilon }_{D}^{2} - {\varepsilon }_{M}^{2}}}{{{{{\varepsilon }}_{D}}{{{\varepsilon }}_{M}}\left( {{{{\varepsilon }}_{D}}{{{\mu }}_{M}} - {{{\varepsilon }}_{M}}{{{\mu }}_{D}}} \right)}}{{c}^{2}}{{{\beta }}^{2}} = 0,$ и для ТЕ-моды ${{{\omega }}^{2}} - \frac{{{\mu }_{D}^{2} - {\mu }_{M}^{2}}}{{{{{\mu }}_{D}}{{{\mu }}_{M}}\left( {{{{\varepsilon }}_{M}}{{{\mu }}_{D}} - {{{\varepsilon }}_{D}}{{{\mu }}_{M}}} \right)}}{{c}^{2}}{{{\beta }}^{2}} = 0.$

Для ППП, которые распространяются вдоль границы немагнитного диэлектрика ${{{\mu }}_{D}} = 1$ и немагнитного металла ${{{\mu }}_{M}} = 1,$ возбуждается только ТМ-мода, для нее имеет место дисперсионное уравнение ${{{\omega }}^{2}}{\tilde {\varepsilon }} - {{c}^{2}}{{{\beta }}^{2}} = 0,$ где ${\tilde {\varepsilon }} = \frac{{{{{\varepsilon }}_{D}}{{{\varepsilon }}_{M}}}}{{{{{\varepsilon }}_{D}} + {{{\varepsilon }}_{M}}}}$ – эффективная диэлектрическая проницаемость. В этом случае ТЕ-мода не возбуждается. Эффективная диэлектрическая проницаемость ${\tilde {\varepsilon }}$ должна быть положительной для ППП, распространяющихся вдоль границы металла с ${\text{Re}}{{{\varepsilon }}_{M}} < 0$ и диэлектрика с ${\text{Re}}{{{\varepsilon }}_{D}} > 0,$ т.е. должны выполняться неравенства ${\text{Re}}{{{\varepsilon }}_{D}}{\text{Re}}{{{\varepsilon }}_{M}} < 0$ и ${\text{Re}}{{{\varepsilon }}_{D}} + {\text{Re}}{{{\varepsilon }}_{M}} < 0.$ При этом действительная часть диэлектрической проницаемости металла должна быть по модулю больше, чем диэлектрическая проницаемость диэлектрика. Тогда постоянная распространения ППП ТМ-моды будет иметь действительное значение ${\beta } = {{k}_{0}}\sqrt {{\tilde {\varepsilon }}} ,$ где ${{k}_{0}} = {{\omega } \mathord{\left/ {\vphantom {{\omega } c}} \right. \kern-0em} c}.$ Постоянные распространения ППП больше по величине, чем волновые векторы фотонов на той же частоте $~{\beta } > {{k}_{0}}.$ Поэтому электромагнитная волна, падающая на плоскую поверхность металла из воздуха, не возбуждает ППП, и для возбуждения ППП необходимо применять соответствующие методы [1–6] для уравнивая тангенциальной компоненты электромагнитной волны и постоянной распространения ППП.

Решения дисперсионного уравнение для ППП ТМ-моды ${{{\varepsilon }}_{D}}{{{\varepsilon }}_{M}}{{{\omega }}^{2}}$ – ${{c}^{2}}\left( {{{{\varepsilon }}_{D}} + {{{\varepsilon }}_{M}}} \right){{{\beta }}^{2}} = 0$ определяют ветви спектра ТМ-моды ППП. На границе раздела сред собственные коллективные электронные колебания (поверхностные электронные состояния или поверхностные плазмоны (ПП)), возникают при резонансе, когда эффективная диэлектрическая проницаемость ${\tilde {\varepsilon }} = {{{{{\varepsilon }}_{D}}{{{\varepsilon }}_{M}}} \mathord{\left/ {\vphantom {{{{{\varepsilon }}_{D}}{{{\varepsilon }}_{M}}} {\left( {{{{\varepsilon }}_{D}} + {{{\varepsilon }}_{M}}} \right)}}} \right. \kern-0em} {\left( {{{{\varepsilon }}_{D}} + {{{\varepsilon }}_{M}}} \right)}} \to \infty .$ Спектр ПП дают решения уравнения ${{{\varepsilon }}_{D}} + {{{\varepsilon }}_{M}} = 0.$ Диэлектрические проницаемости на оптических частотах можно представить для диэлектрика в виде ${{{\varepsilon }}_{D}} = {{1 + {\omega }_{{eD}}^{2}} \mathord{\left/ {\vphantom {{1 + {\omega }_{{eD}}^{2}} {\left( {{\omega }_{0}^{2} - {{{\omega }}^{2}} - i{\Gamma \omega }} \right)}}} \right. \kern-0em} {\left( {{\omega }_{0}^{2} - {{{\omega }}^{2}} - i{\Gamma \omega }} \right)}},$ а для металла в виде ${{{\varepsilon }}_{M}} = {{{\varepsilon }}_{{lat}}}$ – ${{{\omega }_{{eM}}^{2}} \mathord{\left/ {\vphantom {{{\omega }_{{eM}}^{2}} {({{{\omega }}^{2}} + i{\gamma \omega })}}} \right. \kern-0em} {({{{\omega }}^{2}} + i{\gamma \omega })}},$ где ${\omega }_{{ej}}^{2}$ – плазменные частоты, Γ, γ – частоты релаксаций колебаний, ${{\varepsilon }_{{lat}}}$ – диэлектрическая проницаемость ионной решетки металла.

Таким образом, в линейном режиме ППП распространяются в форме эванесцентной волны $\sim {\kern 1pt} {\text{exp}}\left( { - {{{\alpha }}_{D}}x} \right){\text{exp}}\left( { - i{\omega }t + i{\beta }z} \right)$ с гармонической зависимостью от времени и от продольной координаты.

ГИДРОДИНАМИЧЕСКАЯ МОДЕЛЬ

Наиболее последовательно динамика электронов в металле при воздействии электромагнитного поля описывается уравнением Шрёдингера

Из уравнения Шрёдингера (4) с помощью преобразования Маделунга [24] ${\Psi } = a\left( {t,\vec {r}} \right){\text{exp}}\left[ {ib\left( {t,\vec {r}} \right)} \right],$ можно получить гидродинамическую модель, описывающую взаимодействие электронов с электромагнитным полем. Полагая, что ${{a}^{2}} = {{\left| {\Psi } \right|}^{2}} = n\left( {t,\vec {r}} \right)$ – плотность, а $\nabla \phi = \vec {\upsilon }\left( {t,\vec {r}} \right)$ – скорость электронной жидкости, где $\phi = {{ - b\hbar } \mathord{\left/ {\vphantom {{ - b\hbar } m}} \right. \kern-0em} m},$ из уравнения Шрёдингера (4) получаем систему гидродинамических уравнений

где ${{U}_{q}} = - \frac{{{{\hbar }^{2}}}}{{2m}}\frac{{{{\nabla }^{2}}\sqrt n }}{{\sqrt n }}$ – квантовый потенциал, описывающий взаимодействие электронов [1, 13, 25].

Рассмотрим квантовую гидродинамическую модель, в которой градиент потенциала электронной жидкости обусловлен силой Лоренца $ - \nabla U = {{\vec {F}}_{L}},$ а квантовый потенциал представляет кинетическая энергия Томаса–Ферми ${{U}_{q}} = {{C}_{F}}{{n}^{{{5 \mathord{\left/ {\vphantom {5 3}} \right. \kern-0em} 3}}}},$ где ${{C}_{F}} = \frac{{3{{\hbar }^{2}}}}{{10m}}{{\left( {3{{\pi }^{2}}} \right)}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}$ [25]. Тогда уравнения (5), (6) приобретают вид

Для решения системы уравнений (7), (8) можно применить метод последовательных приближений, представляя плотность и скорость электронной жидкости в форме рядов $n\left( {t,\vec {r}} \right) = {{n}_{0}}$ + ${{n}_{1}}\left( {t,\vec {r}} \right) + {{n}_{2}}\left( {t,\vec {r}} \right) + \ldots $ и $\vec {\upsilon }\left( {t,\vec {r}} \right)$ = $ = {{\vec {\upsilon }}_{1}}\left( {t,\vec {r}} \right) + {{\vec {\upsilon }}_{2}}\left( {t,\vec {r}} \right) + \ldots .$ Пренебрегая квантовым давлением по сравнению с силой Лоренца [1] в уравнении (8), получаем уравнения гидродинамической модели в первом приближении

Для ТМ-моды ППП с компонентами поля в немагнитном металле ${{E}_{x}} = \frac{{c{\beta }A}}{{{\omega }{{{\varepsilon }}_{M}}}}\exp \left( {i\phi } \right),$ ${{E}_{z}} = $ $ = i\frac{{c{{{\alpha }}_{M}}A}}{{{\omega }{{{\varepsilon }}_{M}}}}\exp \left( {i\phi } \right),$ ${{B}_{x}} = A\exp \left( {i\phi } \right),$ где $\phi = - i{\omega }t + $ $ + \,\,{{{\alpha }}_{M}}x + i{\beta }z,$ векторное уравнение (10) приобретает вид системы уравнений $\frac{{\partial {{\upsilon }_{{1x}}}}}{{\partial t}} = - \frac{e}{m}{{E}_{x}}$ + $\frac{e}{{mc}}{{\upsilon }_{{1z}}}{{B}_{y}},$ $\frac{{\partial {{\upsilon }_{{1z}}}}}{{\partial t}} = - \frac{e}{m}{{E}_{z}}$ – $\frac{e}{{mc}}{{\upsilon }_{{1x}}}{{B}_{y}},$ а ${{\upsilon }_{{1y}}} = 0.$ Учитывая, что компоненты электрического и магнитного полей имеют одинаковый порядок величины, вторыми слагаемыми в правых частях этих уравнений можно пренебречь [1], т.к. их учет является превышением точности первого приближения. Тогда находим компоненты скорости ${{\upsilon }_{{1x}}} = - i\frac{e}{{m{\omega }}}{{E}_{x}}$ и ${{\upsilon }_{{1z}}} = - i\frac{e}{{m{\omega }}}{{E}_{z}},$ и подставляя в них компоненты ТМ-моды в металле, получаем ${{\upsilon }_{{1x}}} = - i\frac{{eс}}{{m{{{\omega }}^{2}}}} \times $ $ \times \,\,\frac{{{\beta }A}}{{{{{\varepsilon }}_{M}}}}\exp \left( {i\phi } \right),$ ${{\upsilon }_{{1z}}} = \frac{{eс}}{{m{{{\omega }}^{2}}}}\frac{{{{{\alpha }}_{M}}A}}{{{{{\varepsilon }}_{M}}}}\exp \left( {i\phi } \right).$ Подставляя выражения для компонент скорости в уравнение (9) и учитывая, что $\nabla {{\vec {\upsilon }}_{1}} = 0,$ для ТМ-моды ППП получаем ${{\partial {{n}_{1}}} \mathord{\left/ {\vphantom {{\partial {{n}_{1}}} {\partial t}}} \right. \kern-0em} {\partial t}} = 0$ в рассматриваемом приближении, т.е. ${{n}_{1}} = {\text{const}}{\text{.}}$

Во втором приближении система уравнений (7), (8) имеет вид

Систему уравнений (11), (12) с учетом выражения для скорости ${{\vec {\upsilon }}_{1}} = - i\frac{e}{{m{\omega }}}\vec {E}$ представим в виде

Решение уравнения (13) позволяет найти выражение для возмущения электронной плотности во втором приближении на частоте второй гармоники $\sim {\kern 1pt} \exp \left( { - i2{\omega }t} \right),$ ${{n}_{2}} = \frac{{{\omega }_{e}^{2}}}{{4\pi m{{{\omega }}^{4}}}}\nabla \left( {\vec {E}\nabla } \right)\vec {E}$ + $ + \,\,i\frac{{{\omega }_{e}^{2}}}{{4\pi mc{{{\omega }}^{3}}}}\nabla \left( {\vec {E} \times \vec {B}} \right).$ Решение уравнения (14) представляет возмущение электронной скорости во втором приближении ${{\vec {\upsilon }}_{2}} = i\frac{{{{e}^{2}}}}{{2{{m}^{2}}{{{\omega }}^{3}}}}\left( {\vec {E}\nabla } \right)\vec {E}$ – $ - \,\,\frac{{{{e}^{2}}}}{{2{{m}^{2}}c{{{\omega }}^{2}}}}\vec {E} \times \vec {B}.$

Вектор поляризации среды $\vec {P}$ может быть выражен через электронную плотность и вектор плотности тока электронной жидкости, которые связаны уравнением непрерывности $\frac{{\partial n}}{{\partial t}} + \nabla \vec {j} = 0,$ т.е. $\vec {j} = - \frac{1}{e}\frac{{\partial{ \vec {P}}}}{{\partial t}},$ $n = \frac{1}{e}\nabla \vec {P},$ где $\vec {j} = {{n}_{0}}\left( {{{{\vec {\upsilon }}}_{1}} + {{{\vec {\upsilon }}}_{2}}} \right),$ n = = n₀ + n₂. Вектор поляризации среды можно найти как $\vec {P} = - e\int {dt\vec {j}} ,$ т.е.

Следующее приближение увеличивают степень нелинейности тока $\vec {j} = {{n}_{0}}\left( {{{{\vec {\upsilon }}}_{1}} + {{{\vec {\upsilon }}}_{2}} + {{{\vec {\upsilon }}}_{3}}} \right) + {{n}_{2}}{{\vec {\upsilon }}_{1}},$ где возмущение скорости третьего порядка удовлетворяет уравнению

решение которого имеет вид ${{\vec {\upsilon }}_{3}} = - \frac{i}{{3{\omega }}} \times $ $ \times \,\,\left[ {\left( {{{{\vec {\upsilon }}}_{1}}\nabla } \right){{{\vec {\upsilon }}}_{2}} + \left( {{{{\vec {\upsilon }}}_{2}}\nabla } \right){{{\vec {\upsilon }}}_{1}} + \frac{e}{{mс}}{{{\vec {\upsilon }}}_{2}} \times \vec {B}} \right].$ Интегрируя по времени вектор плотности тока $\vec {j},$ полученный в третьем приближении, находим вектор поляризации среды

НЕЛИНЕЙНЫЕ МОДЫ ПОВЕРХНОСТНЫХ ПЛАЗМОН-ПОЛЯРИТОНОВ

Нелинейный отклик возникает в металле при воздействии достаточно мощной электромагнитной волны. Для теоретического анализа нелинейных процессов при распространении ППП полагаем, что ТМ-мода ППП возбуждается на оптической частоте на границе металла с воздухом с диэлектрическим проницаемостями ${{{\varepsilon }}_{M}}$ и ${{{\varepsilon }}_{0}} = 1,$ соответственно. Отклик электронной жидкости на второй гармонике для металла может иметь место на границе раздела сред из-за нарушения трансляционной инвариантности [1], т.е. для компоненты электрического поля ${{E}_{x}}.$ Компоненты поля ППП затухают экспоненциально $\sim {\kern 1pt} {\text{exp}}\left( {{{{\alpha }}_{M}}x} \right)$ вглубь металла ($x < 0$), причем глубина проникновения поля в металл на оптических частотах составляет два-три десятка нанометров при длине волны ППП, имеющей порядок нескольких сотен нанометров. Плотность энергии ППП $\sim {\kern 1pt} {{E}^{2}}$ зависит от нормальной к поверхности металла координаты как ${\text{exp}}\left( {2{{{\alpha }}_{M}}x} \right),$ поэтому энергия ППП сосредоточена вблизи поверхностного слоя.

Процесс формирования мод ППП на границе раздела диэлектрической среды и металла описывается классическими уравнениями Максвелла для поля с учетом нелинейной поляризации электронной жидкости $\nabla \times \vec {B}$ = ${{с}^{{ - 1}}}(\dot {\vec {E}} + 4{\pi }\dot {\vec {P}}),$ $\nabla \times \vec {E} = - {{с}^{{ - 1}}}\dot {\vec {B}}.$ Уравнения для нелинейной ТМ-моды ППП имеют вид $\frac{{d{{B}_{y}}}}{{dz}}$ = $ - {{с}^{{ - 1}}}\left( {{{{\dot {E}}}_{x}} + 4{\pi }{{{\dot {P}}}_{x}}} \right),$ ${{{\alpha }}_{M}}{{B}_{y}} = $ = ${{с}^{{ - 1}}}\left( {{{{\dot {E}}}_{z}} + 4{\pi }{{{\dot {P}}}_{z}}} \right),$ $\frac{{d{{E}_{x}}}}{{dz}} - {{{\alpha }}_{M}}{{E}_{z}} = - {{с}^{{ - 1}}}{{\dot {B}}_{y}},$ где в правых частях стоят компоненты вектора поляризации среды (17). Найти аналитические решения этой системы нелинейных уравнений в частных производных, в правых частях которых имеются члены, зависящие от первой, второй и третьей гармоник частоты возбуждающей ППП электромагнитной волны, весьма проблематично.

Полагаем, что ТМ-мода ППП возбуждается только на первой гармонике, а вторая и третья гармоники в результате дисперсии в металле несинхронны, что возможно при большой величине дисперсии в металле [1], т.е. ППП на них не возбуждаются. Для дальнейшего теоретического анализа нелинейную систему уравнений для компонент ТМ-моды представим с учетом только основных членов [26] вектора поляризации среды (17), дающих наибольший отклик электронной жидкости

где ${{{\varepsilon }}_{{Mx}}} = {{{\varepsilon }}_{{ML}}}$ + $4{\pi }{{{\chi }}_{2}}{{E}_{x}} - 4{\pi }{{{\chi }}_{3}}{{E}^{2}},$ ${{{\varepsilon }}_{{Mz}}} = {{{\varepsilon }}_{{ML}}} - $ $ - \,\,4{\pi }{{{\chi }}_{3}}{{E}^{2}},$ ${{{\varepsilon }}_{{ML}}} = {{{\varepsilon }}_{{lat}}}$ – ${{{\omega }_{{eM}}^{2}} \mathord{\left/ {\vphantom {{{\omega }_{{eM}}^{2}} {({{{\omega }}^{2}} + i{\gamma \omega })}}} \right. \kern-0em} {({{{\omega }}^{2}} + i{\gamma \omega })}},$ ${{{\chi }}_{2}}$ и ${{{\chi }}_{3}}$ – диэлектрическая восприимчивость металла второго и третьего порядков, ${{E}^{2}} = E_{x}^{*}{{E}_{x}} + E_{z}^{*}{{E}_{z}},$ ${{{\alpha }}_{M}}$ и ${{{\varepsilon }}_{{ML}}}$ являются комплексными величинами. Из системы трех уравнений (18), исключая ${{B}_{y}} = - i{{k}_{0}}{\alpha }_{M}^{{ - 1}}{{{\varepsilon }}_{{Mz}}}{{E}_{z}},$ получаем два уравнения для компонент электрического поля нелинейной ТМ-моды

В рассматриваемом случае для нелинейной ТМ-моды ППП ${{{{{\varepsilon }}_{{Mx}}}} \mathord{\left/ {\vphantom {{{{{\varepsilon }}_{{Mx}}}} {{{{\varepsilon }}_{{Mz}}}}}} \right. \kern-0em} {{{{\varepsilon }}_{{Mz}}}}} = 1,$ причем выполняется неравенство $\left| {{{{{E}_{z}}\partial {\text{ln}}{{{\varepsilon }}_{M}}} \mathord{\left/ {\vphantom {{{{E}_{z}}\partial {\text{ln}}{{{\varepsilon }}_{M}}} {\partial z}}} \right. \kern-0em} {\partial z}}} \right| \ll \left| {{{{{E}_{x}}{{{\alpha }}_{M}}{{{\varepsilon }}_{{Mx}}}} \mathord{\left/ {\vphantom {{{{E}_{x}}{{{\alpha }}_{M}}{{{\varepsilon }}_{{Mx}}}} {{{{\varepsilon }}_{{Mz}}}}}} \right. \kern-0em} {{{{\varepsilon }}_{{Mz}}}}}} \right|,$ т.к. ${{{\alpha }}_{M}}\sim {1 \mathord{\left/ {\vphantom {1 {{{x}_{M}}}}} \right. \kern-0em} {{{x}_{M}}}} \gg 1~\,{\text{с}}{{{\text{м}}}^{{ - 1}}}.$ В этом приближении, взяв вторые производные по z в уравнениях (19) и комбинируя эти уравнения с уравнения с первыми производными, систему уравнений первого порядка (19) можно представить в виде системы уравнений второго порядка

В общем случае множитель ${{\kappa }^{2}} = {\alpha }_{M}^{2} + k_{0}^{2}{{{\varepsilon }}_{{ML}}}$ является комплексной величиной. В частном случае, на малых длинах распространения ППП, пропорциональных нескольким длинам волн, когда можно пренебречь затуханием ППП, полагая ${{{\varepsilon }}_{{ML}}}$ и ${{{\alpha }}_{M}}$ действительными величинами, тогда ${{\kappa }^{2}}$ и ${\chi }$ – действительные величины. Введем двухкомпонентный комплексный электрический вектор ТМ-моды ППП $E = {{E}_{x}} + i{{E}_{z}},$ полагая, что ${{E}_{x}}$ и ${{E}_{z}}$ являются действительными величинами. Такой двухкомпонентный вектор можно представить в форме E = $\sqrt {E_{x}^{2} + E_{z}^{2}} {\text{exp}}\left[ {i~{\text{arctg}}\left( {{{{{E}_{z}}} \mathord{\left/ {\vphantom {{{{E}_{z}}} {{{E}_{x}}}}} \right. \kern-0em} {{{E}_{x}}}}} \right)} \right].$ Вектор E вращается в нормальной к поверхности металла плоскости (x, z) (рис. 1а). Систему уравнений (20), (21) представим в виде одного комплексного уравнения для вектора E,

где $\left( {E{\text{*}}E} \right)E = {{E}^{2}}E = {{E}^{3}}.$ Решение нелинейного уравнения (22) имеет вид где ${\text{sn}}\left( {Z + {{\phi }_{0}},\tilde {k}} \right)$ – эллиптический синус Якоби, $Z = {{\left( {{{{\chi }a_{1}^{2}} \mathord{\left/ {\vphantom {{{\chi }a_{1}^{2}} 2}} \right. \kern-0em} 2}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}z,$ ${{\phi }_{0}} = {\text{sn}}\left[ {E\left( 0 \right),\tilde {k}} \right],$ $\tilde {k} = {{{{a}_{2}}} \mathord{\left/ {\vphantom {{{{a}_{2}}} {{{a}_{1}}}}} \right. \kern-0em} {{{a}_{1}}}}$ – модуль эллиптического интеграла [27], $a_{1}^{2} = \frac{1}{\chi } \times $ $ \times \,\,\left\{ {{{\kappa }^{2}}\, + \,{{{\left[ {{{\kappa }^{4}} - 2{\chi }E_{0}^{2}} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right\},$ $a_{2}^{2} = \frac{1}{\chi }\left\{ {{{\kappa }^{2}} - {{{\left[ {{{\kappa }^{4}} - 2{\chi }E_{0}^{2}} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right\},$ $E_{0}^{2} = \left( {{{dE} \mathord{\left/ {\vphantom {{dE} {dz}}} \right. \kern-0em} {dz}}} \right)_{0}^{2}$ + $\left( {{\alpha }_{M}^{2} + k_{0}^{2}{{{\varepsilon }}_{{ML}}}} \right)E{{\left( 0 \right)}^{2}}$ – ${{{\chi }E{{{\left( 0 \right)}}^{4}}} \mathord{\left/ {\vphantom {{{\chi }E{{{\left( 0 \right)}}^{4}}} 2}} \right. \kern-0em} 2}.$ В случае краевых условий $E_{0}^{2} \to 0$ модуль эллиптического интеграла стремится к нулю $\tilde {k} \to 0,$ тогда ${\text{sn}}\left( Z \right) \to {\text{sin}}\left( Z \right),$ т.е. поток ППП имеет форму гармонической волны. В случае, когда $E_{0}^{2} \to {{{{\kappa }^{4}}} \mathord{\left/ {\vphantom {{{{\kappa }^{4}}} {2{\chi }}}} \right. \kern-0em} {2{\chi }}}{\text{,}}$ модуль стремится к единице $\tilde {k} \to 1,$ тогда ${\text{sn}}\left( {Z,1} \right) \to {\text{th}}\left( Z \right)$ при $Z < 0,$ т.е. формируется ударная волна ППП, и ${\text{\;sn}}\left( {Z,1} \right) \to {\text{cth}}\left( Z \right)$ при $Z > 0.$

Выражение (23) для двухкомпонентного электрического вектора в форме эллиптического синуса представляет нелинейную ТМ-моду ППП на границе раздела металла и воздуха. В нелинейном режиме ППП распространяются в форме эванесцентной кноидальной волны $\sim {\kern 1pt} {\text{exp}}\left( {{{{\alpha }}_{M}}x} \right){\text{sn}}\left( {Z + {{\phi }_{0}},\tilde {k}} \right){\text{exp}}\left( { - i{\omega }t} \right)$ с гармонической зависимостью от времени. Огибающие нелинейной ТМ-моды ППП в фиксированный момент времени при разных значениях модуля эллиптического интеграла $\tilde {k}$ представлены на рис. 2.

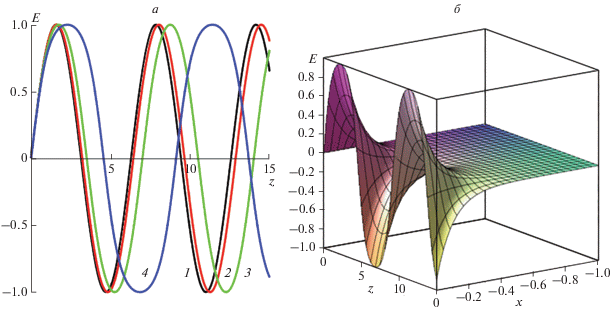
Из анализа вида огибающих нелинейных мод ППП, представленных на рис. 2, следует, что при увеличении значения $E_{0}^{2},$ т.е. модуля $\tilde {k}$ эллиптического интеграла, период ППП волн увеличивается, а форма огибающих меняется. Изменение параметров ТМ-моды ППП возможно с помощью варьирования условий ее возбуждения $\left( {{{dE} \mathord{\left/ {\vphantom {{dE} {dz}}} \right. \kern-0em} {dz}}} \right)_{0}^{2}$ и мощности источника $\sim {\kern 1pt} E{{\left( 0 \right)}^{2}},$ таким образом, можно управлять периодом кноидальной волны, представляющей нелинейную моду ППП.

ЗАКЛЮЧЕНИЕ

Поверхностные плазмон-поляритоны представляют собой гибридные волны, обусловленные взаимодействием фотонов, фононов и свободных электронов (электронной жидкости) на границе раздела диэлектрической и проводящей сред. Квантовая гидродинамическая модель, основанная на преобразовании Маделунга для уравнения Шредингера, позволяет последовательно описать физические механизмы, обуславливающие нелинейный отклик свободных электронов в металле на воздействие внешнего электромагнитного поля.

Динамика ППП зависит от параметров сред и параметров возбуждающей электромагнитной волны. В линейном и в нелинейном режимах на границе раздела немагнитных диэлектрической и проводящей сред формируется ТМ-мода ППП. В линейном режиме формируются гармонические волны, а в нелинейном режиме возникают кноидальные плазмон-поляритонные волны, параметры которых зависят от плотности энергии возбуждающей электромагнитной волны и свойств граничащих сред. Профили огибающих плазмон-поляритонных кноидальных волн и их периоды трансформируются при изменении мощности источника и/или условий возбуждения ППП на границе раздела сред, таким образом периодом нелинейной волны ППП можно управлять.

Работа выполнена при поддержке РНФ (проект № 19-72-20154).