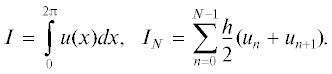Известия РАН. Серия физическая, 2021, T. 85, № 2, стр. 282-288

Прикладные задачи

В физических задачах часто требуется численно находить интегралы. Выделим два класса подынтегральных функций. Первый – периодические функции. Такие задачи возникают при разложении в ряды или интегралы Фурье; они являются некорректными [5]. Поэтому для них необходимо вычислять квадратуры с высокой точностью. Второй класс – функции, быстро убывающие на бесконечности. Приведем примеры таких задач.

1) Передача сигнала. Передать сигнал большого объема дорого. Используют следующий подход. Сигнал разлагают в интеграл Фурье, и в памяти хранят дискретный Фурье образ. Его, в отличие от аналогового сигнала, можно программно сжать без потери информации. Сжатый сигнал передают. По нему восстанавливают Фурье образ и воспроизводят исходный сигнал.

2) Функции Ферми–Дирака. Они зависят от индекса k и параметра x:

Подынтегральная функции быстро убывает на бесконечности. Функции (1) были введены в [6, 7] для описания проводимости твердых металлов. Они являются моментами фермиевского распределения электронов. Затем эти функции были использованы для описания термодинамики плотной горячей плазмы [8]. Сейчас они используются во многих областях физики. Наиболее важны функции с полуцелыми k, но их трудно вычислять.

3) Плазменное микрополе. Хаотическое движение заряженных частиц в плазме создает в ней поля, флуктуирующие на расстояниях порядка межатомных. Именно этими микрополями определяются многие оптические свойства плазмы [9, 10]. Распределение микрополя часто находят, представляя суммарное действие заряженных частиц интегралом Фурье, при этом Фурье образ корректируют с помощью различных модельных предположений. Первой была работа [11], в которой функция распределения равна

4) Скорости реакций. Поведение скоростей термоядерных реакций при низких температурах важно для расчета зажигания дейтериевых мишеней. Для многих ядерных реакций измерены экспериментальные зависимости сечений от скоростей частиц σ(υ). Тогда зависимость скорости реакции от температуры можно найти, усредняя сечение по распределению Максвелла

Подынтегральная функция быстро убывает при υ → ∞.

Вычисление квадратур

Для вычисления квадратур подобных типов в последние годы появился математический метод, ускоряющий вычисления в сотни раз. Оказалось, что для указанных классов функций квадратуры на равномерных сетках сходятся не по степенному закону, а по экспоненциальному. Наиболее полно данная проблема изложена в [1]; там же приведен исчерпывающий список литературы. В [2, 3] экспериментально было показано, что теоретические оценки работы [1] справедливы лишь для функций с полюсами первого порядка.

Опишем полученные результаты. 1) Мажорантную оценку работы [1] можно заметно улучшить. 2) Приведенное в [1] доказательство справедливо лишь для функций с полюсами первого порядка. 3) Найдена эмпирическая оценка погрешности для функций с полюсами порядка выше первого. 4) Эмпирически показано, что зависимость от числа узлов в этих оценках является не мажорантной, а асимптотически точной. Для иллюстрации данных результатов найдены новые точно берущиеся интегралы. Приведены примеры интегралов, для которых погрешность квадратурных формул зависит от шага сетки немонотонно и не описывается существующими теориями.

Мажорирующая константа

Пусть функция постоянна: $u(x) = C.$ Очевидно, для такой функции формула трапеций точна. Поэтому погрешность (5) для функции $u(x) - C$ такова же, как для функции $u(x).$ Однако константа M для функции $u(x) - C$ будет другой. Выберем такую константу C, чтобы минимизировать величину M для новой функции. Для вещественной функции $u(x)$ этот выбор очевиден: $C = 0.5(\max u(x)$ + $\min u(x)).$ Это дает

Легко видеть, что всегда ${{M}_{2}} \leqslant {{{{M}_{1}}} \mathord{\left/ {\vphantom {{{{M}_{1}}} 2}} \right. \kern-0em} 2}.$ Если же $u(x) > 0,$ причем ${{\max u(x)} \mathord{\left/ {\vphantom {{\max u(x)} {\min u(x)}}} \right. \kern-0em} {\min u(x)}}$ близко к 1, то ${{M}_{2}} \ll {{M}_{1}}.$

Аналогичную оценку можно построить для комплексной функции $u(x).$ Рассмотрим значения функции только на вещественном отрезке $x \in [0,2\pi ].$ Положим

Тогда получим оценку

Для вещественных функций оценка (9) переходит в (7). Заметим, что авторы [1] считали свою оценку ${{M}_{1}}$ неулучшаемой.

Апробация оценок

Хотя авторы [1] называют свою оценку мажорантной, фактически они получили гораздо более сильный результат. Наши численные расчеты показали, что если особые точки $u(x)$ являются полюсами первого порядка, то указанная в [1] зависимость от N является асимптотически точной. Опишем эти расчеты.

Для теста был выбран интеграл (6) с $q = 1,$ $r = 10.$ Все особые точки являются полюсами первого порядка. Они расположены в точках

Приведем типичный расчет, в котором выбрано очень малое $L = 0.05$ (ему соответствует $a = {{e}^{L}} \approx 1.051$) и все значения $N = 1,\,\,2,\,\,3,\,\,...$ Результаты показаны на рис. 1 и 2. На рис. 1 показана зависимость логарифма погрешности lg δ от N. Фактическая погрешность показана точками, оценка [1] – треугольниками, оценка [1] с константой ${{M}_{2}}$ – кружками. На начальных участках линий $LN \ll 1,$ и эти участки искривлены. При $LN \gg 1$ линии асимптотически переходят в прямые, что соответствует практически экспоненциальной сходимости. Видно, что наше уточнение константы M улучшает теоретическую оценку.

В данном примере выбрано очень малое L, т.е. особая точка расположена очень близко к вещественной оси. Такой пример считается очень трудным для обычных расчетов. Тем не менее, погрешность стремительно убывает при увеличении N. Уже при $N \approx 400$ она уменьшается до δ ∼ 10^–16. Если же взять $L\sim 1,$ то 16 верных знаков (предельная компьютерная точность) будут получены при $N \approx 20.$ Это наглядно показывает выгоды экспоненциальной сходимости.

На рис. 2 показано отношение оценки [1] с константой ${{M}_{2}}$ к фактической погрешности. Видно, что указанное отношение слегка отличается от константы при $LN < 0.5$ и очень быстро стремится к константе при увеличении N. Это убедительно свидетельствует, что зависимость от N в оценке [1] является не просто мажорантной, а асимптотически точной, и вдобавок применимой при очень малых значениях LN. Это показывает высокую ценность оценки [1].

Практические рекомендации

Из практики расчетов известно, что при степенном характере сходимости $\delta \sim O({{N}^{{ - p}}})$ знак реальной погрешности, начиная с некоторого ${{N}_{0}}$ не меняется при дальнейшем увеличении N. Это является важным свойством, которое позволяет строить оценки точности методом Ричардсона по сгущению сеток.

В данных расчетах мы наблюдали аналогичную картину: погрешность сохраняла свой знак при сгущении сеток. Поэтому здесь также возможно апостериорное определение погрешности по расчетам на сгущающихся сетках. При этом удобно проводить расчеты не при всех N подряд, а только при последовательно удваивающихся N.

Однако сами эти оценки будут другими. Мы используем их при $LN \gg 1,$ когда можно считать δ_N ≈ const ⋅ exp(–LN). В этом случае δ_2N ∼ $O\left( {\delta _{N}^{2}} \right).$ Это напоминает ньютоновскую сходимость, которую обычно называют квадратичной (зачастую не совсем корректно говорят, что число верных знаков удваивается с удвоением N). Это позволяет сформулировать следующую практическую рекомендацию.

Если требуется получить точность ε, то остановим вычисления, как только выполнится условие $\left| {{{I}_{N}} - {{I}_{{2N}}}} \right| < {{\varepsilon }^{{\nu }}},$ где показатель степени выбирают в пределах υ ≈ 0.65–0.75. Меньший показатель может не дать требуемой точности, больший – к избыточным вычислениям или отсутствию сходимости из-за ошибок округления.

Обобщение оценки погрешности

Мы провели тщательный анализ доказательства теоремы [1]. Удалось обнаружить, что при доказательстве теоремы сделано неявное предположение о том, что ближайшая особенность является полюсом первого порядка. Поэтому мы экспериментально исследовали, какова будет погрешность для полюсов целого порядка $q > 1.$ Для исследования был взят тестовый интеграл (6) при $r = 0.$

Численные расчеты показали, что фактическая погрешность при больших N превышает мажорантную оценку [1]. Поскольку эта оценка мажорантна, то превышение означает, что функциональная зависимость погрешности от N должна быть несколько иной. Более тщательный анализ позволил предложить следующую зависимость погрешности от N:

Для полюса первого порядка ($q = 1$) она переходит в оценку [1]. Видно, что при $LN \gg 1$ главным членом является экспонента в знаменателе, то есть погрешность будет близка к экспоненциальной. Наличие множителя ${{(LN)}^{{q - 1}}}$ в числителе несколько замедляет скорость сходимости тем сильнее, чем больше q, т.е. чем сильнее особенность. Тем не менее, сходимость очень быстра.

Апробация оценки

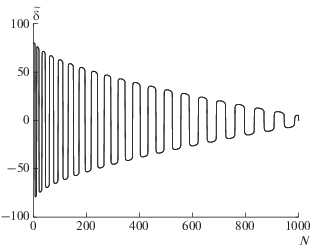
Результаты расчетов тестового интеграла показаны на рис. 3. По оси абсцисс, как и на рис. 2, отложен логарифм отношения теоретической оценки (11) к фактической погрешности расчета. Около каждой кривой указана кратность полюса q. Для сравнения приведена кривая для $q = 1.$

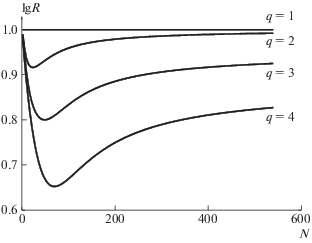
Видно, что линия $q = 1$ горизонтальна. Остальные линии – кривые с минимумом, переходящие в горизонтальные линии при увеличении N. Это показывает, что предложенная оценка (11) является асимптотически точной по N. Выход на асимптоту происходит тем медленнее, чем больше q. Из высот горизонтальных асимптот видно, что при $q = 1$ и $q = 2$ теоретическая оценка в ~10 раз больше фактической погрешности. При $q = 3$ превышение составляет ~8.5 раз; при $q = 4$ оно равно ~6.6 раз. Такие превышения показывают, что функциональная зависимость погрешности от N, L, q близка к истинной, но использование константы ${{M}_{2}}$ приводит к слишком большому превышению (константа ${{M}_{1}}$ даст еще худшие результаты).

Отметим, что в этих расчетах реальная погрешность сохраняет свой знак при увеличении N, как это было для полюса кратности 1. Поэтому здесь остаются в силе те же практические рекомендации по выбору сеток и критерию окончания расчета для получения заданной точности.

Новые тестовые интегралы

В [1] были рассмотрены непериодические функции на бесконечной прямой. Сформулированы условия, при которых соответствующие квадратуры сходятся экспоненциально. Найдены мажорантные оценки их погрешности.

Для верификации этих оценок необходимо иметь тестовые примеры с такими подынтегральными функциями, при которых интегралы выражаются через элементарные функции. Мы построили четыре таких интеграла, значения которых ранее были неизвестны. Приведем их без вывода.

В этих интегралах функция имеет существенно особую точку при $x = 0$ (то есть эта точка совпадает с концом отрезка интегрирования), а также бесконечно удаленную особую точку. Интегралы с такими особенностями возникают, например, при вычислении скоростей химических или ядерных реакций по их сечению в термодинамически равновесной среде.

Этот случай не подпадает под теорему [1], поскольку в ней предполагалось, что особая точка не лежит на отрезке интегрирования (хотя расстояние до отрезка интегрирования может быть сколь угодно малым). В связи с отсутствием теоретических оценок численный расчет таких примеров становится особенно интересным.

Пример расчета

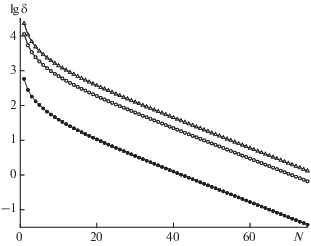
Для интеграла (15) были проведены численные расчеты для сеток с $N = 1,2,...,1000.$ Было найдено точное значение погрешности $\delta = \left| {I - {{I}_{N}}} \right|.$ Оказалось, что зависимость этой величины от N кардинально отличается от ранее рассмотренных случаев. Эта зависимость знакопеременна и затухает по амплитуде.

Для передачи такой зависимости был найден специфический масштаб. По оси ординат откладывалась величина

здесь μ – величина наименьшего из экстремумов. На рис. 4 показана погрешность в данном масштабе. Такой масштаб линейно изображает погрешность в малой окрестности нулевых значений, но логарифмически уменьшает ее вдали от нулей.

Такой вид погрешности, во-первых, не описывается ни одной из известных теорий. Во-вторых, к нему не применимы все известные методы апостериорного нахождения погрешности расчета. Видно, что подобные задачи требуют развития новых теоретических подходов.

Бесконечно удаленная особенность

Если подынтегральная функция имеет только бесконечно удаленную особую точку, то это должно быть антиподом только что рассмотренного примера. Следует ожидать очень быстрой сходимости квадратур. Рассмотрим следующий тестовый пример:

Этот пример также выходит за рамки теоремы [1]. Расчет показывает, что сходимость квадратурных формул оказывается качественно быстрее экспоненциальной. Она подчиняется закону ${{\delta }_{{2N}}}\sim O(\delta _{N}^{4}).$

Особая точка подынтегральной функции (17) является существенно особой. Тем не менее, сходимость оказывается исключительно быстрой. Это показывает, что характер сходимости определяется не столько типом особенности, сколько ее расположением. Чем дальше особая точка находится от отрезка интегрирования, тем сходимость быстрее. Расположение особой точки на отрезке кардинально ухудшает сходимость.