Известия РАН. Серия физическая, 2021, T. 85, № 2, стр. 276-281
Применение голографической интерферометрии для передачи информации через возмущенную океаническую среду
В. М. Кузькин 1, М. Бади 2, С. А. Пересёлков 3, *, Е. С. Казначеева 3
1 Федеральное государственное бюджетное учреждение науки Федеральный исследовательский центр
“Институт общей физики имени А.М. Прохорова Российской академии наук”
Москва, Россия
2 Университет штата Делавер
Ньюарк, США
3 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Воронежский государственный университет”
Воронеж, Россия
* E-mail: pereselkov@yandex.ru
Поступила в редакцию 28.08.2020
После доработки 25.09.2020
Принята к публикации 28.10.2020
Аннотация
Теория интерферометрической обработки гидроакустической информации обобщена на случай, когда интенсивные внутренние волны обусловливают взаимодействие мод поля источника. Дано объяснение экспериментальным данным по формированию голограммы при наличии интенсивных внутренних волн. Оценена погрешность передачи неискаженной информации через возмущенную океаническую среду.
ВВЕДЕНИЕ
Интерферометрическая обработка [1–3] основана на когерентном накоплении спектральной интенсивности волнового поля вдоль локализованных полос интерференционной картины (интерферограммы) в переменных частота–время, формируемой широкополосным источником, которая далее подвергается двукратному преобразованию Фурье. На выходе интегрального преобразования спектральная плотность концентрируется в узкой полосе в форме фокальных пятен, обусловленных интерференцией мод различных номеров. В отличие от сигнала, накопление помехи вдоль полос интерферограммы не когерентно и распределено по всей области двукратного интегрального преобразования. Восстановление зашумленной интерферограммы достигается фильтрацией двумерной спектральной плотности сигнала с последующим применением к ней двукратного обратного преобразования Фурье. Преобразованную спектральную плотность интерферограммы назовем голограммой, а саму обработку – голографической интерферометрией, позволяющей выделять слабые сигналы на фоне интенсивной помехи. Регулярный характер интерференционной картины, позволяющей реализовать такую обработку, обусловлен волноводной дисперсией и многомодовым распространением звуковых волн.
Наиболее очевидным применением голографической интерферометрии является локализация малошумных источников [1–3]. На ее основе разработаны два адаптивных алгоритма интерферометрической обработки, которые решают проблему локализации малошумных источников в условиях, когда отсутствует априорная информация о передаточной функции океанической среды [4–6].
Другое представляющее интерес применение голографической интерферометрии связано с возможностью передачей неискаженной гидроакустической информации через случайно-неоднородную океаническую среду. Впервые данный эффект экспериментально обнаружен при прохождении широкополосного сигнала стационарной трассы, возмущенной интенсивными внутренними волнами (ИВВ), в эксперименте SWARM-95 [7, 8] и описан в работах [9, 10].
В настоящей работе на основе теоретического анализа и численного моделирования изучен механизм формирования интерферограммы и голограммы, когда ИВВ приводят к взаимодействию мод поля источника. Объяснен экспериментальный эффект [10] образования двух непересекающихся областей голограммы, обусловленных невозмущенным и рассеянным полями. Оценена погрешность восстановления интерферограммы невозмущенного поля.
ФОРМИРОВАНИЕ ГОЛОГРАММЫ В ПРИСУТСТВИИ ИВВ
Теоретическое обоснование избежания искажений информации при наличии гидродинамических возмущений опирается на возможность представления интерферограммы в виде линейной суперпозиции двух независимых интерферограмм, порожденных невозмущенным и рассеянным полями. Тогда, согласно свойству линейности двукратного преобразования Фурье, на голограмме формируются две неперекрывающиеся локализованные спектральные области. Одна из них, обусловленная невозмущенным полем, концентрируется в форме фокальных пятен преимущественно в направлении оси времени, а вторая, вызванная гидродинамическим возмущением, – в направлении оси частоты. Фильтрация этих областей позволяет разрешить голограммы невозмущенного и рассеянного полей. Применение к ним обратного двукратного преобразования Фурье дает возможность реконструировать их интерферограммы. Одна из них обусловлена интерференцией мод невозмущенной среды, другая – изменчивостью среды.
В условиях, когда моды нельзя считать независимыми, вариации показателя преломления инициируют обмен энергии между их комплексными амплитудами. Изменения фазы, определяющей вид локализованных полос интерферограммы, обусловлены изменениями как горизонтальных волновых чисел, так и амплитуд мод. Поправки фазы по отношению к невозмущенному значению можно определить методом малых возмущений, позволяющим описать слабую межмодовую трансформацию, характерную для океанических неоднородностей.
Для простоты ограничимся рассмотрением ИВВ в форме одиночного солитона, распространяющегося вдоль акустической трассы. Поправки комплексных амплитуд ${{A}_{m}}$ определяются из системы линейных дифференциальных уравнений первого порядка для взаимодействующих мод
(1)
$\frac{{d{{A}_{m}}\left( {x,t} \right)}}{{dx}} = i\sum\limits_n {\left\{ {{{\xi }_{m}}{{{\delta }}_{{mn}}} + {{{\mu }}_{{mn}}}\left( {x,t} \right)} \right\}} {{A}_{n}}\left( {x,t} \right),$Коэффициенты взаимодействия мод равны
(2)
${{{\mu }}_{{mn}}}\left( {x,t} \right) = \frac{{\bar {k}_{0}^{2}}}{{2\sqrt {{{{\bar {h}}}_{m}}{{{\bar {h}}}_{n}}} }}\int\limits_0^H {{{{\bar {\psi }}}_{m}}\left( z \right){{{\bar {\psi }}}_{n}}\left( z \right){{{\tilde {n}}}^{2}}\left( {x,z,t} \right)dz} .$Здесь $\bar {k}_{0}^{2}$ – квадрат волнового числа на глубине $z = 0,$ ${{\bar {\psi }}_{m}}\left( z \right)$ – собственная функция m-й моды. Флуктуационная компонента квадрата показателя преломления записывается как
(3)
${{\tilde {n}}^{2}}\left( {x,z,t} \right) = - 2Q{{N}^{2}}\left( z \right)\Phi \left( z \right)\zeta \left( {x,t} \right),$(4)
$\zeta \left( {x,t} \right) = - B{\text{sec}}{{{\text{h}}}^{2}}\left[ {{{\left( {x - ut} \right)} \mathord{\left/ {\vphantom {{\left( {x - ut} \right)} \eta }} \right. \kern-0em} \eta }} \right].$Здесь B и η – амплитуда и полуширина солитона на уровне 0.42 от максимума, u – скорость распространения.
Учитывая малость ${{\tilde {n}}^{2}}$ по отношению к ${{\bar {n}}^{2}},$ ${{\tilde {n}}^{2}} \ll {{\bar {n}}^{2}},$ результирующее поле p представим как
где ${{p}_{0}}$ – невозмущенное поле, удовлетворяющее волновому уравнению(6)
$\Delta p\left( {x,z,t} \right) + \bar {k}_{0}^{2}\left( {{{{\bar {n}}}^{2}}\left( z \right) + {{{\tilde {n}}}^{2}}\left( {x,z,t} \right)} \right)p\left( {x,z,t} \right) = 0$с соответствующими граничными условиями при ${{\tilde {n}}^{2}}\left( {x,z,t} \right) = 0$, ${{p}_{s}}$ − рассеянное поле первого порядка относительно ${{\tilde {n}}^{2}}$. Запишем поля ${{p}_{{0,s}}}$ как сумму мод вида
(7)
${{p}_{0}}\left( {\omega } \right) = \sum\limits_m {{{{\bar {A}}}_{m}}} \left( {\omega } \right){\text{exp}}\left( {i{{{\bar {h}}}_{m}}\left( {\omega } \right){{x}_{0}}} \right),$(8)
$\begin{gathered} {{p}_{s}}\left( {{\omega },t} \right) = \sum\limits_m {{{{\tilde {A}}}_{m}}} \left( {{\omega },t} \right){\text{exp}}\left( {i{{\Phi }_{m}}\left( {{\omega },~t} \right)} \right),~ \\ 0 \leqslant x\left( t \right) \leqslant {{x}_{0}}.~ \\ \end{gathered} $Здесь ${{\Phi }_{m}}\left( {{\omega },~t} \right) = \int_0^{x\left( t \right)} {{{{\tilde {h}}}_{m}}} \left( {{\omega },~t} \right)dx{\kern 1pt} '$ − фаза m-моды рассеянного поля, ${{x}_{0}}$ − расстояние между источником и приемником. Поправки ${{\tilde {A}}_{m}}$ и ${{\tilde {h}}_{m}}$ определяются из решения системы уравнений (1). Цилиндрическое расхождение поля, модальное затухание, глубины источника ${{z}_{s}}$ и приемника ${{z}_{q}}$ формально учитываются амплитудной зависимостью мод.
Интерферограмма результирующего поля I = = |p|2, согласно (5), равна
где звездочкой обозначена комплексно-сопряженная величина. Первое и четвертое слагаемые представляют собой интерферограммы невозмущенного и рассеянного полей, а второе и третье слагаемые − интерферограммы, вызванные произведением невозмущенного и рассеянного полей. Невозмущенное и рассеянное поля некогерентны, поэтому второе и третье слагаемые можно рассматривать как некий фон (среднее значение), снижающий контрастность результирующей интерферограммы.Вычтем из интерферограммы I (9) среднее значение $\bar {\bar {I}}$, $\dddot I = I - \bar {\bar {I}}$. Тогда
(10)
$\dddot I\left( {{\omega },t} \right) = {{\dddot I}_{0}}\left( {\omega } \right) + {{\dddot I}_{s}}\left( {{\omega },t} \right).~$Согласно (7), (8),
(11)
$\begin{gathered} {{{\dddot I}}_{0}}\left( {\omega } \right) = \sum\limits_m {\sum\limits_n {{{{\bar {A}}}_{m}}} } \left( {\omega } \right)\bar {A}_{n}^{*}\left( {\omega } \right){\text{exp}}\left( {i{{{\bar {h}}}_{{mn}}}\left( {\omega } \right){{x}_{0}}} \right) = \\ = \sum\limits_m {\sum\limits_n {\dddot I_{0}^{{\left( {mn} \right)}}} } \left( {\omega } \right),~\,\,m \ne n,~ \\ \end{gathered} $(12)
$\begin{gathered} {{{\dddot I}}_{s}}\left( {{\omega },t} \right)\sum\limits_m {\sum\limits_n {{{{\tilde {A}}}_{m}}} } \left( {{\omega },x\left( t \right),t} \right)\tilde {A}_{n}^{*}\left( {{\omega },x\left( t \right),t} \right) \times \\ \times \,\,{\text{exp}}\left( {i\int\limits_0^{x\left( t \right)} {{{{\tilde {h}}}_{{mn}}}} \left( {{\omega },t} \right)dx{\kern 1pt} '} \right) = \\ = \sum\limits_m {\sum\limits_n {\dddot I_{s}^{{\left( {mn} \right)}}} } \left( {{\omega },t} \right),\,\,\,\,~m \ne n.~ \\ \end{gathered} $Здесь ${{\bar {h}}_{{mn}}} = {{\bar {h}}_{m}} - {{\bar {h}}_{n}},$ ${{\tilde {h}}_{{mn}}} = {{\tilde {h}}_{m}} - {{\tilde {h}}_{n}}{\kern 1pt} .$ Таким образом, при наличии возмущения интерферограмма представляет собой сумму интерферограмм невозмущенного и рассеянного полей.
Применим к интерферограмме $\dddot I\left( {{\omega },t} \right)$ (10) двукратное преобразование Фурье. В результате получаем сумму голограмм невозмущенного и рассеянного полей
(13)
$\begin{gathered} F\left( {\mathop \nu \limits^\prime ,~{\tau }} \right) = \sum\limits_m {\sum\limits_n {\int\limits_0^{\Delta t} {\int\limits_{{{{\omega }}_{1}}}^{{{{\omega }}_{2}}} {\left[ {\dddot I_{0}^{{\left( {mn} \right)}}\left( {\omega } \right) + \dddot I_{s}^{{\left( {mn} \right)}}\left( {{\omega },t} \right)} \right]} } } } \times \\ \times \,\,{\text{exp}}\left[ {i\left( {\mathop \nu \limits^\prime t - {\tau \omega }} \right)} \right]dtd{\omega } = \\ = \sum\limits_m {\sum\limits_n {F_{0}^{{\left( {mn} \right)}}} } \left( {\mathop \nu \limits^\prime ,{\tau }} \right) + \sum\limits_m {\sum\limits_n {F_{s}^{{\left( {mn} \right)}}} } \left( {\mathop \nu \limits^\prime ,{\tau }} \right). \\ \end{gathered} $Здесь $\mathop \nu \limits^\prime = 2{\pi }$ и τ − циклическая частота и время голограммы; $\Delta t$ − время наблюдения; ω1, 2 = = ${{{\omega }}_{0}} \mp \left( {{{\Delta {\omega }} \mathord{\left/ {\vphantom {{\Delta {\omega }} 2}} \right. \kern-0em} 2}} \right)$, $\Delta {\omega }$ и ${{{\omega }}_{0}}$ − ширина и средняя частота спектра.
Используя подход при получении голограммы движущегося источника [1], для парциальной голограммы невозмущенного поля находим
(14)
$\begin{gathered} F_{0}^{{\left( {mn} \right)}}\left( {\mathop \nu \limits^\prime ,{\tau }} \right) = {{{\bar {A}}}_{m}}\left( {{{{\omega }}_{0}}} \right)\bar {A}_{n}^{*}\left( {{{{\omega }}_{0}}} \right)\Delta {\omega }\Delta t \times \\ \times \,\,{\text{exp}}\left( {i{{\mathop \nu \limits^\prime \Delta t} \mathord{\left/ {\vphantom {{\mathop \nu \limits^\prime \Delta t} 2}} \right. \kern-0em} 2}} \right){\text{exp}}\left\{ {i\left[ {\left( {m - n} \right){{x}_{0}}{\alpha } - {\tau }{{{\omega }}_{0}}} \right]} \right\} \times \\ \times \,\,\frac{{{\text{sin}}\left( {\frac{{\mathop \nu \limits^\prime \Delta t}}{2}} \right)}}{{\left( {\frac{{\mathop \nu \limits^\prime \Delta t}}{2}} \right)}}\frac{{{\text{sin}}\left[ {\left( {\left( {m - n} \right){{x}_{0}}\frac{{d{\alpha }}}{{d{\omega }}} - {\tau }} \right)\frac{{\Delta {\omega }}}{2}} \right]}}{{\left[ {\left( {\left( {m - n} \right){{x}_{0}}\frac{{d{\alpha }}}{{d{\omega }}} - {\tau }} \right)\frac{{\Delta {\omega }}}{2}} \right]}},~ \\ \end{gathered} $Вычисление парциальной голограммы рассеянного поля (13) возможно лишь численными методами. Однако и без численного решения можно получить некоторые общие выводы относительно расположения на голограмме области локализации рассеянного поля. Положим, что в интерферограмме рассеянного поля (12) амплитуды ${{\tilde {A}}_{{m,n}}}$ медленно меняются с изменением частоты и времени по сравнению с “быстрым” экспоненциальным множителем. Тогда парциальную голограмму рассеянного поля можно представить как
(15)
$\begin{gathered} F_{s}^{{\left( {mn} \right)}}\left( {\mathop \nu \limits^\prime ,{\tau }} \right) = \sum\limits_m {\sum\limits_n {{{{\tilde {A}}}_{m}}} } \left( {{{{\omega }}_{0}},{{t}_{1}}} \right)\tilde {A}_{n}^{*}\left( {{{{\omega }}_{0}},{{t}_{1}}} \right) \times \\ \times \,\,\int\limits_0^{\Delta t} {\int\limits_{{{{\omega }}_{1}}}^{{{{\omega }}_{2}}} {\left[ {{\text{exp}}\left( {i{{\Phi }_{{mn}}}\left( {{\omega },~t} \right)} \right){\text{exp}}\left( {i\left( {\mathop \nu \limits^\prime t - {\tau \omega }} \right)} \right)} \right]} } dtd{\omega }.~ \\ \end{gathered} $Если в разности фаз ${{\Phi }_{{mn}}}\left( {{\omega },t} \right)$ = ${{\Phi }_{m}}\left( {{\omega },t} \right) - {{\Phi }_{n}}\left( {{\omega },t} \right)$ можно пренебречь изменениями частоты, то спектральная плотность рассеянного поля концентрируется вдоль оси частоты $\mathop \nu \limits^\prime $. Данный эффект ранее наблюдался в натурном эксперименте [10]. В противном случае, когда эту зависимость необходимо учитывать, спектральная плотность будет располагаться в узкой полосе под некоторым углом к оси частоты.
Таким образом, в присутствии ИВВ на голограмме реализуются две неперекрывающиеся области спектральной плотности невозмущенного и рассеянного полей. Применение к отфильтрованным спектральным плотностям обратных двукратных преобразований Фурье дает возможность реконструировать двумерные интерферограммы невозмущенного и рассеянного полей.
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ
Использовался невозмущенный горизонтально-однородный волновод, близкий по характеристикам экспериментальному каналу [7, 8]. Рассматривались два диапазона частот: $\Delta {{f}_{1}} = 100{\kern 1pt} - {\kern 1pt} 120$ Гц и $\Delta {{f}_{2}} = 300{\kern 1pt} - {\kern 1pt} 320$ Гц. Параметры жидкого поглощающего дна: отношение плотности грунта и воды ${\rho } = 1.8$; для первого диапазона частот комплексный показатель преломления $n = 0.84\left( {1 + i0.03} \right)$, для второго − $n = 0.84\left( {1 + i0.05} \right)$. Расстояние между неподвижными источником и приемником ${{x}_{0}} = 10$ км. Источник располагался на глубине ${{z}_{s}} = 12.5$ м, приемник − на глубине ${{z}_{q}} = 35$ м. Задавался равномерный спектр, импульсы регистрировались с периодичностью 5 с, дискретизация по частоте спектра принимаемого сигнала 0.25 Гц. Единичный солитон перемещался вдоль трассы в направлении от приемника к источнику. Параметры солитона: амплитуда $B = 15$ м, ширина $\eta = 150$ м, скорость $w = 0.7$ м/с. Время наблюдения $\Delta t = 20$ мин. Результаты моделирования приведены на рис. 1−4. С целью повышения контрастности и информативности на интерферограммах вырезаны средние значения.
Рис. 1.
Нормированные интерферограммы (а, в) и модули голограмм (в, г) невозмущенных полей: (а, б) полоса $\Delta {{f}_{1}}$, (в, г) полоса $\Delta {{f}_{2}}$.
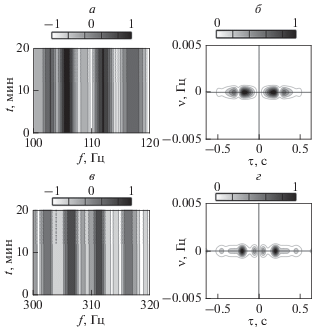
На рис. 1 представлены интерферограммы и модули голограмм для невозмущенных полей, т.е. когда солитон располагался вне стационарной трассы. С точностью до постоянного множителя интерферограмма невозмущенного поля является передаточной функцией волновода.
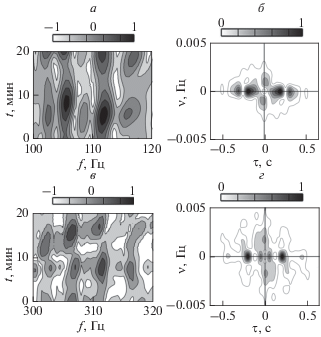
Интерферограммы и модули голограмм для начального момента времени наблюдения, когда солитон удален на расстояние ${{x}_{*}} = 5$ км от источника, приведены на рис. 2. За время наблюдения $\Delta t = 20$ мин солитон прошел расстояние $\Delta x = 840$ м. На низких частотах, когда рассеяние на неоднородности мало, в результирующей интерферограмме преобладают вертикальные локализованные полосы (рис. 2а), характерные невозмущенному волноводу. С повышением частоты̀ эффекты рассеяния возрастают, усиливается вклад интерференции мод рассеянного поля, что приводит к формированию горизонтальных локализованных полос (рис. 2в). В результате интерференционная картина усложняется. На голограммах спектральные плотности невозмущенного и рассеянного полей в форме фокальных пятен сконцентрированы вдоль осей времени τ и частоты ν (рис. 2б, 2г). Вне этих пятен спектральная плотность практически подавлена. Механизм расположения фокальных пятен делает возможным восстановление интерферограмм невозмущенного и рассеянного полей.
Рис. 2.
Нормированные интерферограммы (а, в) и модули голограмм (б, г), когда солитон расположен на трассе: (а, б) полоса $\Delta {{f}_{1}}$, (в, г) полоса $\Delta {{f}_{2}}$.
Фильтрация спектральных плотностей голограмм невозмущенного поля, сосредоточенных вблизи оси времени, и их образ Фурье показаны на рис. 3. Интерферограммы и топография расположения локализованных областей на голограммах невозмущенных полей в отсутствие солитона и восстановленных близки между собой (см. рис. 1). Максимумы расположения фокальных пятен совпадают. Наиболее ярко близость их интерферограмм иллюстрирует рис. 4.
Рис. 3.
Нормированные отфильтрованные модули голограмм (а, в) невозмущенного поля и восстановленные по ним интерферограммы (б, г): (а, б) полоса $\Delta {{f}_{1}}$, (в, г) полоса $\Delta {{f}_{2}}$.
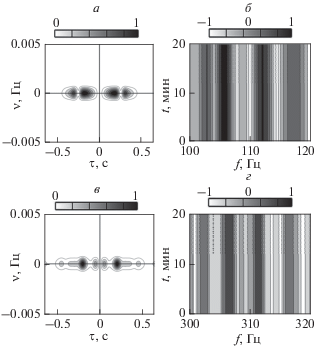
Рис. 4.
Зависимости нормированных интерферограмм невозмущенных полей от частоты в отсутствие солитона (сплошная линия) и реконструированные при его наличии (точки).
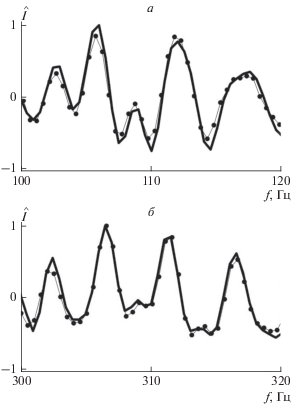
На рис. 4 приведены одномерные интерферограммы невозмущенных полей в отсутствие солитона на трассе (сплошная линия) и реконструированные (точки), когда солитон движется по трассе. Интерферограммы представляют собой горизонтальные сечения двумерных интерферограмм (рис. 1, 3). Погрешность восстановления интерферограмм оценивалась как
(16)
$d = \frac{{\sum\limits_{j = 1}^J {\left| {{{I}_{1}}\left( {{{f}_{j}}} \right) - {{I}_{2}}\left( {{{f}_{j}}} \right)} \right|} }}{{\sum\limits_{j = 1}^J {\left| {{{I}_{1}}\left( {{{f}_{j}}} \right)} \right|} }},~$ЗАКЛЮЧЕНИЕ
В условиях взаимодействия мод акустического поля источника, вызванного проявлением одиночного солитона, применяя голографическую интерферометрию, доказана возможность восстановления интерферограммы невозмущенного поля. Обработка основана на записи результирующей голограммы, формируемой невозмущенным и рассеянным полями, которая представляет собой непересекающиеся локализованные области спектральных плотностей, отвечающих отсутствию и наличию возмущения. Считывание этих областей путем обратного двукратного преобразования Фурье позволяет реконструировать интерферограмму невозмущенного поля с малыми искажениями.
Работа выполнена при поддержке РФФИ (проекты № 19-29-06075 и № 19-38-90326).
Список литературы
Кузнецов Г.Н., Кузькин В.М., Пересёлков С.А. // Акуст. журн. 2017. Т. 63. № 4. С. 406; Kuznetsov G.N., Kuz’kin V.M., Pereselkov S.A. // Acoust. Phys. 2017. V. 63. No 4. P. 449.
Кузнецов Г.Н., Кузькин В.М., Пересёлков С.А. // Изв. РАН. Сер. физ. 2017. Т. 81. № 8. С. 1041; Kuznetsov G.N., Kuz’kin V.M., Pereselkov S.A. // Bull. Russ. Acad. Sci. Phys. 2017. V. 81. No 8. P. 938.
Казначеев И.В., Кузнецов Г.Н., Кузькин В.М. Пересёлков С.А. // Акуст. журн. 2018. Т. 64. № 1. С. 33; Kaznacheev I.V., Kuznetsov G.N., Kuz’kin V.M., Pereselkov S.A. // Acoust. Phys. 2018. V. 64. No 1. P. 37.
Kaznacheeva E.S., Kuznetsov G.N., Kuz’kin V.M. et al. // Phys. Wave Phenom. 2019. V. 27. No 1. P. 73.
Kaznacheeva E.S., Kuz’kin V.M., Lyakhov G.A. et al. // Phys. Wave Phenom. 2020. V. 28. No 3. P. 267.
Пересёлков С.А., Кузькин В.М., Кузнецов Г.Н. // Изв. РАН. Сер. физ. 2020. Т. 84. № 6. С. 794; Pereselkov S.A., Kuz’kin V.M., Kuznetsov G.N. // Bull. Russ. Acad. Sci. Phys. 2020. V. 84. No 6. P. 648.
Apel J.R., Badiey M., Chiu C.-S. et al. // IEEE J. Ocean. Eng. 1997. V. 22. P. 465.
Frank S.D., Badiey M., Lynch J., Siegmann W.L. // JOSA. 2004. V. 116. No 6. P. 3404.
Kuz’kin V.M., Pereselkov S.A., Zvyagin V.G. et al. // Phys. Wave Phenom. 2018. V. 26. No 2. P. 160.
Badiey M., Kuz’kin V.M., Lyakhov G.A. et al. // Phys. Wave Phenom. 2019. V. 27. No 4. P. 313.
Кацнельсон Б.Г., Петников В.Г. Акустика мелкого моря. М.: Наука, 1997. 192 с.
Флатте С. Распространение звука во флуктуирующем океане. М.: Мир, 1982. 336 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая


