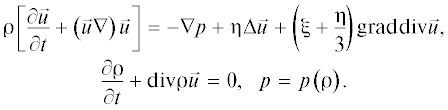Известия РАН. Серия физическая, 2021, T. 85, № 6, стр. 804-810
Поля радиационных сил в слое вязкой жидкости
В. А. Гусев 1, 2, Д. А. Жарков 1, *
1 Федеральное государственное бюджетное образовательное учреждение высшего образования
Московский государственный университет имени М.В. Ломоносова
Москва, Россия
2 Федеральное государственное бюджетное учреждение науки
Институт физики Земли имени О.Ю. Шмидта Российской академии наук
Москва, Россия
* E-mail: denis.Zharkov2014@yandex.ru
Поступила в редакцию 09.12.2020
После доработки 25.01.2021
Принята к публикации 26.02.2021
Аннотация
Приводятся результаты расчета поля поверхностной акустической волны в системе “слой вязкой жидкости–упругая подложка” с учетом сдвиговых компонент в жидкости. Рассмотрен механизм радиационного давления, действующий на жидкость и связанный с нелинейностью уравнений гидродинамики. Рассчитаны пространственные распределения силы радиационного давления, возникающей в вязкой жидкости со стороны стоячей поверхностной волны. Показано, что учет вязкости вызывает дополнительную силу, направленную к центру системы, а сдвиговые компоненты приводят к значительным градиентам радиационного давления вблизи границы раздела сред.
ВВЕДЕНИЕ
Решение ряда актуальных прикладных задач требует развития методик и устройств, позволяющих формировать материалы и структуры с заранее заданными свойствами и параметрами [1–6]. Проведенные ранее экспериментальные исследования [7, 8] показали возможность и эффективность методики, основанной на формировании стоячей поверхностной акустической волны (ПАВ) в жидком слое на упругой подложке.
Радиационные силы в жидкости, вызванные акустическим воздействием, находят широкое применение. Отметим здесь акустическую левитацию взвешенных в жидкости частиц [9, 10] и силовое воздействие на такие частицы [11]. При этом вопрос о влиянии вязкости на структуру формируемых в жидком слое радиационных сил не был полностью решен. В работах [7, 12] показано, что учет затухания потенциальной компоненты ПАВ в жидком слое слабо сказывается на дисперсионных характеристиках волны. Однако сдвиговые компоненты ПАВ в вязкой жидкости учтены не были, что привело к неточной записи граничных условий, а следовательно, и дисперсионного уравнения, и амплитудных характеристик. В то же время ясно, что сдвиговые компоненты будут локализованы вблизи границы раздела сред и могут оказать существенное влияние на характеристики волны. Расчеты скорости поверхностной волны и затухания проведены в работах [13, 14], однако этих результатов недостаточно для вычисления радиационных сил.
Целью данной работы является расчет поля ПАВ и формируемых ими радиационных сил в слоистых структурах с учетом вязкости и их сравнение с результатами, полученными ранее без учета вязкости. Далее поля поверхностных волн рассчитываются на основе линеаризованной системы уравнений движения вязкой жидкости и теории упругости. Затем рассчитывается тензор радиационного давления на основе представления, полученного усреднением уравнений гидродинамики по быстрым движениям в рамках квадратично-нелинейного приближения. Основная новизна работы связана с учетом сдвиговых компонент поля ПАВ в жидком слое и расчетом радиационных сил с их учетом.
АКУСТИЧЕСКОЕ ПОЛЕ В СИСТЕМЕ “ЖИДКИЙ СЛОЙ–УПРУГОЕ ПОЛУПРОСТРАНСТВО”
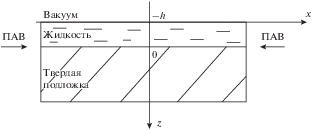
Пусть упругая среда занимает полупространство z ≥ 0, при этом ось z направлена вниз (рис. 1). Выше границы раздела сред в слое –h < z < 0 находится вязкая жидкость. Сверху при –∞ < z < –h находится вакуум. Вдоль границы раздела сред z = = 0 в положительном и отрицательном направлениях оси x распространяются навстречу друг другу две поверхностные волны одинаковой частоты, формируя стоячую волну. При этом поля этих встречных волн будут симметричны относительно точки x = 0. Далее для простоты ограничимся рассмотрением двумерной задачи.
Акустическое поле в вязком жидком слое описывается системой уравнений Навье–Стокса, непрерывности и состояния:
Здесь $\vec {u}$ – вектор колебательной скорости частиц жидкости, ${{\rho }}$ – плотность, $p$ – давление, ${{c}_{0}}$ – скорость звука в жидкости, ${{\xi }}$ и  – коэффициенты объемной и сдвиговой вязкости соответственно, t – время, $\Delta $ – лапласиан.
– коэффициенты объемной и сдвиговой вязкости соответственно, t – время, $\Delta $ – лапласиан.
Нелинейные члены системы (1) играют определяющую роль в формировании поля радиационного давления и вызываемых им течений в рамках рассматриваемого ниже механизма. Однако радиационное давление является квадратичным эффектом по акустическому полю ПАВ, и учет нелинейных членов для поля ПАВ приведет в выражениях для радиационного давления к величинам третьего и выше порядков малости по числу Маха. Это выходит за пределы точности модели, учитывающей квадратичную нелинейность. Поэтому при расчете акустического поля ПАВ нелинейными слагаемыми пренебрегается и используется линеаризованная система уравнений:
(2)
$\begin{gathered} {{{{\rho }}}_{0}}\frac{{\partial{ \vec {u}}}}{{\partial t}} = - \nabla p{\kern 1pt} '\, + {{\eta }}\Delta \vec {u} + \left( {{{\xi }} + \frac{{{\eta }}}{3}} \right){\text{grad}}~{\text{div}}\vec {u}, \\ \frac{{\partial \rho {\kern 1pt} '}}{{\partial t}} + {{\rho }_{0}}{\text{div}}\vec {u} = 0,\,\,\,\,p{\kern 1pt} ' = {{\rho }}{\kern 1pt} {\text{'}}c_{0}^{2}. \\ \end{gathered} $Здесь ${{{{\rho }}}_{0}}$ и ${{\rho }}{\kern 1pt} {\text{'}}$ – равновесная плотность и ее акустическое приращение, $p{\kern 1pt} '$ – акустическое давление.
Применяемая методика расчета поля поверхностной волны в целом аналогична стандартной [15] и отличается, главным образом, учетом сдвиговых компонент в жидкости. Удобно ввести скалярный потенциал φ и векторный потенциал $\vec {A}$ поля в жидкости в соответствии с представлением $\vec {u} = \nabla {{\varphi }} + {\text{rot}}\vec {A}.$ Подставляя это выражение в систему (2) и применяя поочередно операции дивергенции и ротора, получим уравнения для потенциалов:
(3)
$\frac{{{{\partial }^{2}}{{\varphi }}}}{{\partial {{t}^{2}}}} - c_{0}^{2}\Delta {{\varphi }} = \frac{b}{{{{{{\rho }}}_{0}}}}\Delta \frac{{\partial {{\varphi }}}}{{\partial t}},\,\,\,\,b = {{\xi }} + \frac{4}{3}{{\eta }},$В рассматриваемой двумерной задаче отсутствует зависимость от координаты y и uy = 0. Единственной отличной от нуля компонентой векторного потенциала является Ay ≡ A, т.е. $\vec {A} = \{ 0,A,0\} $ и векторное уравнение (4) сводится к скалярному.
В упругом полупространстве поле смещений $\vec {U} = \left( {U,~V = 0,W} \right)$ = 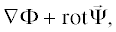 $U = \frac{{\partial {{\Phi }}}}{{\partial x}} - \frac{{\partial {{\Psi }}}}{{\partial z}},$ W = = $\frac{{\partial {{\Phi }}}}{{\partial z}} + \frac{{\partial {{\Psi }}}}{{\partial x}}$ также описываем скалярным Φ и векторным ${{\vec {\Psi }}}$ = {0, Ψ, 0} потенциалами, подчиняющимися волновым уравнениям [12, 15].
$U = \frac{{\partial {{\Phi }}}}{{\partial x}} - \frac{{\partial {{\Psi }}}}{{\partial z}},$ W = = $\frac{{\partial {{\Phi }}}}{{\partial z}} + \frac{{\partial {{\Psi }}}}{{\partial x}}$ также описываем скалярным Φ и векторным ${{\vec {\Psi }}}$ = {0, Ψ, 0} потенциалами, подчиняющимися волновым уравнениям [12, 15].
Удобно представить искомую стоячую ПАВ в виде суммы двух бегущих волн, распространяющихся навстречу друг другу, и вначале рассчитать поле этих волн. Поле второй получается изменением знака волнового числа. Отыскиваем решение уравнений (3) и (4), соответствующее гармонической поверхностной волне, бегущей вдоль оси x и локализованной вблизи границы раздела z = 0, вида $ \sim {\kern 1pt} {{e}^{{ - i({{\omega }}t - kx)}}}.$ Здесь ω – частота, $k = \frac{\omega }{c},$ c – искомая скорость поверхностной волны. Выражение для встречной бегущей волны получаем с помощью замены k → –k. В результате получаем следующие решения для потенциалов поля в жидком слое:
(5)
$\begin{gathered} {{\varphi }} = \left( {{{B}_{1}}{{e}^{{ - irz}}} + {{B}_{2}}{{e}^{{irz}}}} \right){{e}^{{ - i\left( {{{\omega }}t - kx} \right)}}}, \\ A = \left( {{{C}_{1}}{{e}^{{ - i{{\kappa }}z}}} + {{C}_{2}}{{e}^{{i{{\kappa }}z}}}} \right){{e}^{{ - i\left( {{{\omega }}t - kx} \right)}}}, \\ \end{gathered} $(6)
$\begin{gathered} {\text{Ф}} = D{{e}^{{ - qz}}}{{e}^{{ - i\left( {{{\omega }}t - kx} \right)}}},\,\,\,\,{{\Psi }} = F{{e}^{{ - sz}}}{{e}^{{ - i\left( {{{\omega }}t - kx} \right)}}}, \\ q = \sqrt {{{k}^{2}} - k_{l}^{2}} ,\,\,\,\,s = \sqrt {{{k}^{2}} - k_{t}^{2}} . \\ \end{gathered} $Здесь введены волновые числа kl = $\frac{\omega }{{{{c}_{l}}}}$ – для продольных волн и kt = $\frac{\omega }{{{{c}_{t}}}}$ – для поперечных волн.
Для определения параметров поверхностной волны необходимо добавить граничные условия, позволяющие найти скорость волны. Поскольку в рассматриваемой системе существует 6 волн (две потенциальные и две сдвиговые компоненты в жидком слое, а также две компоненты в упругом полупространстве), то и граничных условий должно быть 6: равенство нормальных и касательных смещений и напряжений на границе “жидкий слой–упругое полупространство” и равенство нулю нормальных и касательных напряжений на свободной поверхности жидкости [14]. Подстановка потенциалов (5) и (6) в эти граничные условия приводит к дисперсионному уравнению $\det \Delta \left( k \right) = 0,$ матрица $\Delta \left( k \right)$ которого имеет вид:
Поскольку определитель теперь становится комплексным, то определяемая из дисперсионного уравнения скорость волны получает мнимую добавку, которая интерпретируется как появление затухания волны. Зависимости скорости и коэффициента затухания от толщины слоя и частоты рассчитаны в работе [14].
Амплитуды встречных бегущих волн также находятся с помощью матрицы $\Delta \left( k \right)$ (с учетом замены $k \to - k$ для встречных волн), для чего необходимо исключить одно из уравнений в силу их линейной зависимости, а затем применить формулы Крамера. Складывая поля бегущих волн, получаем поле искомой стоячей ПАВ. Однако выражения для поля в вязком слое оказываются слишком громоздкими, поэтому приведем зависимости колебательной скорости и давления в стоячей волне для случая идеальной жидкости, чтобы прояснить основную структуру поля [12]:
(7)
$\begin{gathered} {{u}_{x}} = \frac{k}{r}{{U}_{0}}\sin r\left( {z + h} \right)\sin kx\sin {{\omega }}t, \\ {{u}_{z}} = - {{U}_{0}}\cos r\left( {z + h} \right)\cos kx\sin {{\omega }}t, \\ p{\kern 1pt} ' = - \frac{{{{{{\rho }}}_{0}}{{\omega }}}}{r}{{U}_{0}}\sin r\left( {z + h} \right)\cos kx\cos {{\omega }}t, \\ {{U}_{0}} = \frac{{2{{\omega }}q}}{{\cos rh}}\frac{{k_{t}^{2}}}{{\left( {{{k}^{2}} + {{s}^{2}}} \right)}}{{V}_{0}}. \\ \end{gathered} $РАДИАЦИОННОЕ ДАВЛЕНИЕ В ВЯЗКОЙ ЖИДКОСТИ
На взвешенные в жидкости частицы действует радиационная сила со стороны акустического поля. Обычно радиационную силу в этом случае связывают с разностью импульсов, действующих на частицу с разных сторон [16–19]. Когда волна падает на частицу, то она рассеивается, и импульсы с передней и задней сторон различаются. В результате усреднения получается ненулевая сила, направленная в сторону уменьшения импульса. При этом нелинейный параметр жидкости в выражения для радиационного давления не входит и, следовательно, нелинейность уравнений гидродинамики никак не влияет на этот механизм. Но эта сила для частицы с радиусом R и плотностью ρ пропорциональна (kR)4 и для наночастиц несущественна. Таким образом, можно ожидать, что наночастицы увлекаются жидкостью и их относительным движением можно пренебречь. Действительно, в работе [12] получены оценки характерных значений параметров, определяющих поведение наночастицы в акустическом поле, в частности, времени затухания движения частиц относительно жидкости:
В первом слагаемом величина $\frac{{2{{{{\rho }}}_{0}}{{R}^{2}}}}{{9{{\eta }}}}$ для частиц диоксида кремния размером порядка 200 нм [7] оказывается равной ~10–8–10–9 с, поправка, связанная с частотой, незначительна (~0.1, вплоть до ~1) и не влияет на порядок величины. Второе слагаемое имеет приблизительно такой же порядок ~10–8 с. Такие времена соответствуют частотам порядка сотен мегагерц. Соответственно, для частоты порядка десятков мегагерц параметр ${{{{\omega }}}_{0}}{{t}_{0}}.$ является малой величиной. Это означает, что при воздействии акустических полей с частотами порядка десятков мегагерц и ниже можно пренебречь собственным движением частиц малого размера и считать, что частицы полностью увлекаются жидкостью.
Поэтому при расчете радиационной силы на взвешенные наночастицы на первый план выступает другой механизм [12], связанный с нелинейностью уравнений гидродинамики и действующий именно на элемент объема жидкости. Наличие нелинейных слагаемых приводит при усреднении по периоду акустической волны к появлению ненулевой силы – собственно радиационной силы. При отсутствии нелинейных членов усреднение, очевидно, давало бы ноль для периодических процессов. Соответственно, радиационное давление в этом механизме определяется не параметрами частиц, а нелинейностью исходных уравнений акустического поля в жидкости. Радиационные силы, в свою очередь, вызывают акустические течения, увлекающие частицы. Если частицы малы (наночастицы), то они полностью увлекаются жидкостью и перемещаются вместе с ней.
Для расчета радиационного давления на элемент объема жидкости и акустических течений предложены различные модели, которым посвящено множество работ. Для определенности будем исходить из результатов работы [20]. В ней на основе гидродинамического подхода и процедуры разделения быстрых и медленных движений из полной системы уравнений механики сплошной среды (1) с учетом нелинейных слагаемых получено выражение для тензора радиационных напряжений в случае вязкой жидкости [20]:
(8)
$\begin{gathered} {\text{П}}_{{ik}}^{{RAD}} = \frac{{{\varepsilon }}}{{{{{{\rho }}}_{0}}c_{0}^{2}}}\left\langle {{{p}^{{'2}}}} \right\rangle {{{{\delta }}}_{{ik}}} + {{{{\rho }}}_{0}}\left\langle {{{u}_{i}}{{u}_{k}}} \right\rangle + \frac{{{\eta }}}{{{{{{\rho }}}_{0}}c_{0}^{2}}}\frac{\partial }{{\partial {{x}_{k}}}}\left\langle {p{\kern 1pt} '{{u}_{i}}} \right\rangle + \\ + \,\,\frac{{{{\xi }} + {{{\eta }} \mathord{\left/ {\vphantom {{{\eta }} 3}} \right. \kern-0em} 3}}}{{{{{{\rho }}}_{0}}c_{0}^{2}}}{{{{\delta }}}_{{ik}}}\frac{\partial }{{\partial {{x}_{l}}}}\left\langle {p{\kern 1pt} '{{u}_{l}}} \right\rangle . \\ \end{gathered} $Здесь угловые скобки означают усреднение по периоду акустической волны, ε – параметр нелинейности жидкости. Радиационная сила ${{F}_{i}},$ действующая на элемент объема жидкости, выражается через тензор ${{\Pi }_{{ik}}}{\text{:}}$
Для вывода выражения (8) нужно разделить медленные гидродинамические и быстрые акустические переменные, полагая ρ = ρ0 + ρ', p = = $P + c_{0}^{2}{{\rho }}{\kern 1pt} {\text{'}} + {{\varepsilon }}\frac{{{{{{\rho }}}^{{{\text{'2}}}}}}}{{c_{0}^{2}{{{{\rho }}}_{{\text{0}}}}}},$ ${{u}_{i}} = {{U}_{i}} + u_{i}^{'},$ где величины со штрихом относятся к акустическим переменным, а Ui – скорость усредненного движения (акустического течения), возникающего за счет радиационного давления. Здесь уравнение состояния, связывающее давление и плотность, также учитывает квадратичную нелинейность. Проведя усреднение, выделив уравнения для среднего и осциллирующего движений и найдя приближенное решение для осциллирующего движения, можно прийти к выражению (8). Подчеркнем еще раз, что тензор радиационных напряжений (8) появляется именно из-за нелинейности уравнений гидродинамики. В то же время акустические поля допустимо рассчитывать в линейном приближении, чтобы оставаться в рамках квадратично-нелинейных эффектов.
Влияние вязкости жидкости проявляется в нескольких факторах. Во-первых, появляется затухание потенциальной компоненты поля ПАВ, во‑вторых, появляются сдвиговые компоненты поля ПАВ, в-третьих, в тензоре радиационных напряжений (8) появляется дополнительное слагаемое. Ясно, что относительная роль первого и третьего факторов пропорциональна коэффициентам вязкости, и для слабовязких жидкостей они не должны приводить к радикальному изменению радиационных сил. Амплитуда же сдвиговых компонент – второй фактор – вблизи границы раздела сред должна быть одного порядка по сравнению с амплитудами других компонент ПАВ. Именно роль сдвиговых компонент может быть недооценена. Поэтому далее проведем сравнение пространственных распределений радиационной силы, создаваемой стоячей ПАВ, для трех случаев: (а) для идеальной жидкости без вязкости, (б) для приближенной модели жидкости с учетом вязкости для продольной компоненты и без учета сдвиговых компонент (формально положено C1 = C2 = 0) – рис. 2, (в) для точной модели с учетом сдвиговых компонент – рис. 3.
Рис. 2.
Пространственное распределение радиационной силы с учетом вязкости для потенциальной
компоненты и без учета сдвиговых компонент для частоты (1/2π) кГц при 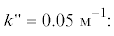 (а) x-компонента, (б) z-компонента.
(а) x-компонента, (б) z-компонента.

Рис. 3.
Пространственное распределение радиационной силы с учетом сдвиговых компонент для частоты (1/2π) кГц: (а) x-компонента, $0 \leqslant kz \leqslant 0.5,$ (б) x-компонента, $0 \leqslant kz \leqslant 0.00005,$ (в) z-компонента, $0 \leqslant kz \leqslant 0.5,$ (г) z-компонента, $0 \leqslant kz \leqslant 0.00005.$

При расчетах задавались следующие параметры: плотность жидкости – 1000 кг/м3, плотность подложки – 2700 кг/м3, скорость звука в жидкости с0 = 1400 м/с, в твердом теле: сl = 7650 м/с, сt = = 4500 м/с, η = 0.0004 Па ⋅ с, ξ = 0.001 Па ⋅ с, b = = 0.0015 Па · с, ε = 3.5, 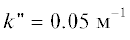 (
(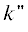 ‑ мнимая часть волнового числа, ответственная за затухание волны; при построении
увеличена относительно расчетного значения при заданных η и ξ, чтобы показать роль
затухания вдоль оси x). Частота волн принята равной (1/2π) кГц, толщина слоя 5 м. В этом случае получаем
два решения дисперсионного уравнения – высокоскоростное c = 4142 м/с и низкоскоростное c = 1592 м/с, соответствующие различным модам поверхностной волны в жидком слое. На
рис. 2–3 представлены результаты расчетов для высокоскоростной волны, поскольку она обладает
большей длиной волны, равной примерно 26 м, и, соответственно, именно она образует
крупномасштабную структуру поля. Для сравнения приведем скорость рэлеевской волны
на границе упругой подложки и вакуума cR = 4126 м/с и скорость волны Стоунли на границе упругого и жидкого полупространств
cS = 1399.4 м/с.
‑ мнимая часть волнового числа, ответственная за затухание волны; при построении
увеличена относительно расчетного значения при заданных η и ξ, чтобы показать роль
затухания вдоль оси x). Частота волн принята равной (1/2π) кГц, толщина слоя 5 м. В этом случае получаем
два решения дисперсионного уравнения – высокоскоростное c = 4142 м/с и низкоскоростное c = 1592 м/с, соответствующие различным модам поверхностной волны в жидком слое. На
рис. 2–3 представлены результаты расчетов для высокоскоростной волны, поскольку она обладает
большей длиной волны, равной примерно 26 м, и, соответственно, именно она образует
крупномасштабную структуру поля. Для сравнения приведем скорость рэлеевской волны
на границе упругой подложки и вакуума cR = 4126 м/с и скорость волны Стоунли на границе упругого и жидкого полупространств
cS = 1399.4 м/с.
На рис. 2 представлены горизонтальная и вертикальная компоненты радиационной силы без учета сдвиговых компонент. Видно, что вдоль оси x образуется квазипериодическая структура. Если вязкостью пренебречь полностью, то формируется периодическое синусоидальное распределение. В данном случае за счет затухания акустических волн радиационная сила увеличивается при удалении от центра структуры, т.е. появляется дополнительная сила, направленная к середине при x = 0 (точке симметрии встречных поверхностных волн). Это может способствовать более эффективному сбору взвешенных частиц вблизи этой области. Интересно также отметить, что на некоторой глубине z в жидком слое радиационная сила оказывается равной нулю. При переходе через нуль происходит изменение полярности (или сдвиг на полпериода) пространственного распределения обеих компонент силы, положения минимумов и максимумов меняются местами. Поэтому с точки зрения формирования упорядоченных структур необходимо более детально исследовать поле вблизи границы раздела. При этом для горизонтальной компоненты наибольшее значение силы наблюдается как раз в области вблизи границы. Для вертикальной компоненты, наоборот, ее значения вблизи границы меньше, а положение нуля силы располагается значительно ближе к самой границе. Это означает, что формирование упорядоченных структур происходит, в основном, именно в этой сравнительно небольшой области.
Пространственная структура радиационных сил с учетом сдвиговых компонент проиллюстрирована на рис. 3. Из графиков видно, что на расстояниях, меньших длины волны, происходит экспоненциальное затухание поля. Видно, что учет сдвиговых компонент приводит к появлению значительных сил, сосредоточенных вблизи границы раздела сред. Это связано с быстрым затуханием и, соответственно, большим градиентом поля. Важно подчеркнуть, что условие прилипания вязкой жидкости к упругому полупространству здесь автоматически выполняется в силу учета соответствующего граничного условия. Движение среды и соответствующие радиационные силы связаны с тем, что сама граница движется относительно лабораторной системы отсчета при распространении поверхностной волны (или колебаниях в стоячей волне). Хотя область локализации сдвиговых компонент весьма мала, достигаемые большие значения радиационной силы могут привести в среднем к существенному воздействию на характер движения жидкости, причем именно в области вблизи границы. Они могут определять формирующуюся на подложке структуру при испарении жидкого слоя со взвешенными частицами и, таким образом, являться основным управляющим фактором на последнем этапе процесса самоорганизации ансамблей этих частиц.
ЗАКЛЮЧЕНИЕ
Таким образом, рассчитаны с учетом сдвиговых компонент дисперсионные и амплитудные характеристики поверхностной волны в слое вязкой жидкости, а также радиационные силы, действующие на элемент объема жидкости и увлекаемые им взвешенные частицы. Рассмотрен механизм радиационного давления на элемент объема жидкости, обусловленный нелинейностью уравнений гидродинамики. Проведено сравнение трех случаев: (1) без вязкости, (2) с вязкостью, но без учета сдвиговых компонент и (3) с учетом сдвиговых компонент. Показано, что вязкость приводит к значимым изменениям пространственной структуры радиационных сил и может привести к улучшению условий образования упорядоченных ансамблей наночастиц. Дополнительная радиационная сила, обусловленная сдвиговыми компонентами акустического поля в жидкости, сосредоточена в узком слое вблизи границы раздела сред, в которой и происходит формирование упорядоченных ансамблей частиц. Поэтому достигаемые радиационной силой в этой области значительные величины будут являться одним из основных факторов, определяющих движение жидкости и параметры формирующейся структуры. В дальнейшем планируется рассчитать вызванные радиационным давлением акустические течения и движение взвешенных наночастиц в этих течениях.
Работа поддержана РФФИ (проект № 20-02-00493).
Список литературы
Sarvazyan A.P., Rudenko O.V., Nyborg W.L. // Ultrasound Med. Biol. 2010. V. 36. No. 9. P. 1379.
Wixforth A. // Superlat. Microstruct. 2003. V. 33. P. 389.
Strobl C.J., Guttenberg Z.V., Wixforth A. // IEEE Trans. Ultrason. Ferroelectr. Freq. Contr. 2004. V. 51. P. 1432.
Lebedev-Stepanov P.V., Rudenko O.V. // Acoust. Phys. 2009. V. 55. No. 6. P. 729.
Бадмаев Б.Б., Дамдинов Б.Б., Дембелова Т.С. // Изв. РАН Сер. физ. 2015. Т. 79. № 10. С. 1461; Badmaev B.B., Damdinov B.B., Dembelova T.S. // Bull. Russ. Acad. Sci. Phys. 2015. V. 79. P. 1301.
Макарова Д.Н., Дембелова Т.С., Бадмаев Б.Б. // Акуст. журн. 2020. Т. 66. № 6. С. 610; Makarova D.N., Dembelova T.S., Badmaev B.B. // Acoust. Phys. 2020. V. 66. No. 6. P. 613.
Rudenko O.V., Lebedev-Stepanov P.V., Gusev V.A. et al. // Acoust. Phys. 2010. V. 56. No. 6. P. 935.
Макалкин Д.И., Коршак Б.А., Брысев А.П. // Акуст. журн. 2017. Т. 63. С. 553; Makalkin D.I., Korshak B.A., Brysev A.P. // Acoust. Phys. 2017. V. 63. No. 5. P. 590.
Суханов Д.Я., Росляков С.Н., Емельянов Ф.С. // Акуст. журн. 2020. Т. 66. № 2. С. 154; Sukhanov D.Ya., Roslyakov S.N., Emel’yanov F.S. // Acoust. Phys. 2020. V. 66. No. 2. P. 137.
Li J., Liu C.J., Zhang W.J. // Acoust. Phys. 2017. V. 63. No. 1. P. 125.
Николаева А.В., Цысарь С.А., Сапожников О.А. // Акуст. журн. 2016. Т. 62. № 1. С. 29; Nikolaeva A.V., Tsysar S.A., Sapozhnikov O.A. // Acoust. Phys. 2016. V. 62. No. 1. P. 38.
Гусев В.А., Руденко О.В. // Акуст. журн. 2019. Т. 65. № 2. С. 166; Gusev V.A., Rudenko O.V. // Acoust. Phys. 2010. V. 56. No. 6. P. 861.
Волькенштейн М.М., Левин В.М. // Акуст. журн. 1988. № 4. С. 34; Vol’kenshtein M.M., Levin V.M. // Sov. Phys. Acoust. 1988. V. 34. No. 4. P. 351.
Gusev V.A., Simonova P.A. // Phys Wave Phenom. 2015. V. 23. No. 4. P. 268.
Викторов И.А. Звуковые поверхностные волны в твердых телах. М.: Наука, 1981. 288 с.
Горьков Л.П. // ДАН СССР. 1961. Т. 140. № 1. С. 88; Gor’kov L.P. // Sov. Phys. Dokl. 1961. No. 6. P. 773.
Гольдберг З.А. // В кн.: Мощные ультразвуковые поля. Т. 2. М.: Наука, 1968. С. 49.
Андреев В.Г., Демин И.Ю., Корольков З.А., Шанин А.В. // Изв. РАН Сер. физ. 2016. Т. 80. № 10. С. 1321; Andreev V.G., Demin I.Yu., Korolkov Z.A., Shanin A.V. // Bull. Russ. Acad. Sci. Phys. 2016. V. 80. No. 10. P. 1191.
Диденкулов И.Н., Корчагина Т.С., Прончатов-Рубцов Н.В., Сагачева А.А. // Изв. РАН Сер. физ. 2020. Т. 84. № 6. С. 772; Didenkulov I.N., Korchagina T.S., Pronchatov-Rubtsov N.V., Sagacheva A.A. // Bull. Russ. Acad. Sci. Phys. 2020. V. 84. P. 634.
Руденко О.В. // В кн.: Нелинейные проблемы теории колебаний и теории управления. Вибрационная механика. СПб.: Наука, 2009. С. 402.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая