Известия РАН. Серия физическая, 2021, T. 85, № 6, стр. 811-816

ВВЕДЕНИЕ

На сегодняшний день в области медицинской акустики быстро развивается направление неинвазивной хирургии, в котором мощные фокусированные ультразвуковые пучки используются для разрушения заданных структур организма внутри тела человека, например, опухолей [1]. При проектировании преобразователей для генерации мощного ультразвука и определения эффективности и безопасности терапевтического воздействия возникает задача моделирования нелинейных звуковых пучков [2]. В большинстве случаев излучателем генерируется монохроматическая волна, спектр которой в процессе распространения обогащается высшими гармониками за счет эффектов акустической нелинейности. Одним из часто используемых уравнений для моделирования ультразвуковых пучков является нелинейное уравнение Вестервельта. Теоретическая модель, основанная на данном уравнении, позволяет количественно точно описывать нелинейные ударно-волновые поля, создаваемые фокусированными преобразователями мощного ультразвука в однородных поглощающих средах [3, 4]. Однако в общем случае для решения данного уравнения, когда эволюционной переменной выступает время, необходимо использование суперкомпьютерных мощностей [5].

Для оптимизации численного эксперимента по распространению нелинейных фокусированных ультразвуковых пучков создаются специальные алгоритмы. В данной работе рассматривается важный для практики случай направленного трехмерного пучка. В этом случае возможен переход в бегущую систему координат, ось которой ориентирована вдоль преимущественного направления распространения волны в пучке, т.е. вдоль оси z (рис. 1). Благодаря такому переходу уравнение Вестервельта принимает вид эволюционного уравнения, выражающего первую производную акустического давления по осевой координате через комбинацию членов, которую можно считать известной для заданного z. Обычно численное решение уравнения такого типа строится с использованием метода расщепления по физическим факторам [6], согласно которому на каждом шаге по координате z вдоль преимущественного направления распространения волны каждый физический эффект рассчитывается отдельно с помощью определенного метода. Типовой размер матриц для хранения поля давления может достигать N_x = 10 000 на N_y = 10 000 (рис. 1) для каждой из N_max = 1000 гармоник профиля нелинейной волны [7]. Даже при учете сделанных упрощений количество данных и соответствующая сложность расчетов требуют использования суперкомпьютерных мощностей.

Путем оптимизации распределения высших гармоник по пространству удается снизить требования к количеству оперативной памяти, в результате чего задача может быть решена на ПК с многоядерными центральными процессорами (CPU) [7]. Однако даже в случае параллельного исполнения вычислений на нескольких ядрах процессора (обычно от 2 до 16), ускоряющих расчеты в примерно соответствующее число раз, один расчет может занимать до нескольких суток. Это происходит из-за необходимости проведения вычислительных действий с большим количеством данных на каждом шаге алгоритма. При этом для характеризации поля одного излучателя во всем диапазоне мощностей обычно требуется провести несколько десятков расчетов [4]. Помимо быстроты расчетов, использование вычислений на ПК также ограничено оперативной памятью процессора. В случае нехватки памяти на проведение вычислений с имеющимся количеством данных происходит обмен данными с жестким диском, что значительно замедляет алгоритм и делает расчеты нецелесообразными. Потенциальным способом решения проблемы скорости вычислений является использование графических процессоров (GPU), имеющих до нескольких тысяч узкоспециализированных ядер и позволяющих выполнять достаточно широкий спектр математических операций [8]. Однако увеличение числа ядер не обязательно ускоряет вычисления в соответствующее число раз. Это обусловлено тем, что ядра на GPU менее мощные, и, соответственно, их производительность и скорость вычисления ниже по сравнению с ядрами CPU. Кроме того, хранение и запись данных при выполнении каждого из шагов алгоритма вдоль эволюционной координаты производится в оперативной памяти CPU, что приводит к необходимости обмена данными между центральным и графическим процессорами на каждом шаге алгоритма, на что уходит дополнительное время. В силу данных особенностей архитектуры GPU важной задачей становится нахождение баланса между максимальными размерами обрабатываемых на данном шаге алгоритма данных, которые помещаются в оперативную память графического процессора во избежание их передачи по частям, и минимизацией обмена данными между оперативной памятью центрального и графического процессоров.

Целью данной работы являлась разработка алгоритма, реализующего численные расчеты эффектов акустической нелинейности, дифракции и поглощения в однонаправленном уравнения Вестервельта на графических процессорах (GPU), что позволит ускорить решение задачи моделирования нелинейных ультразвуковых пучков.

ТЕОРЕТИЧЕСКАЯ МОДЕЛЬ

Уравнение Вестервельта в бегущей системе координат можно записать в эволюционной форме как:

где p(x, y, z, τ) – акустическое давление, ${{c}_{0}}$ – скорость звука в среде, $\tau = t - {z \mathord{\left/ {\vphantom {z {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}}$ – время в бегущей системе координат, $\beta $ – коэффициент нелинейности, $\delta $ – коэффициент термовязкого поглощения [3, 4]. Дифференциальные операторы в правой части уравнения в порядке слева направо описывают эффекты дифракции, нелинейности и термовязкого поглощения.

При численном решении уравнения (1) на каждом шаге по z дискретизованное поле давления $p\left( {x,y,z,\tau } \right)$ представлено в памяти ЭВМ в виде трехмерной матрицы, которая содержит набор комплексных амплитуд N_max гармоник спектра волны в разложении ее профиля в конечный ряд Фурье в каждой пространственной точке плоскости xy на сетке с числом точек N_x и шагом Δx по оси x и N_y с шагом Δy по оси y:

где круговые частоты гармоник ${{\omega }_{n}} = \omega n,$ $\omega $ – круговая частота монохроматического источника, ${{p}_{n}}$ – комплексные амплитуды гармоник. Отметим, что в памяти ЭВМ достаточно хранить только одну половину спектра (по положительным частотам), т.к. вторая половина по отрицательным частотам является комплексно-сопряженной к первой.

Как было указано ранее, на CPU данная задача решается достаточно долго, и в настоящее время все большую популярность приобретает использование графических процессоров, для работы с которыми уже адаптировано большое количество алгоритмов. Преимущество графических процессоров (GPU) заключается в том, что они содержат до нескольких тысяч небольших ядер, способных выполнять максимально много арифметических операций одновременно, в то время как в составе центральных процессоров присутствует несколько мощных ядер, выполняющих максимально широкий набор инструкций [8]. Для современных GPU уже реализованы библиотеки многих стандартных математических операций и методов, связанных, например, с линейной алгеброй и быстрым преобразованием Фурье (БПФ).

Рассмотрим физические эффекты, входящие в уравнение (1), по отдельности. Эффект дифракции описывается следующим уравнением [9]:

где $\Delta = \frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}$ – оператор Лапласа. Тогда для комплексной амплитуды одной гармоники дифракционное уравнение (3) запишется в виде: где ${{k}_{n}} = {{{{\omega }_{n}}} \mathord{\left/ {\vphantom {{{{\omega }_{n}}} {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}}$ – волновое число. При решении уравнения (4) методом углового спектра амплитуды пространственного спектра находятся при помощи прямого БПФ от двумерного распределения поля гармоники ${{p}_{n}}\left( {x,y,z} \right)$ на данном расстоянии z от источника: где $x = m\Delta x,$ $y = l\Delta y.$ Умножение амплитуд спектра на пропагатор, соответствующий уравнению (4), дает решение для амплитуд на следующей плоскости, отстоящей от предыдущей на шаг ∆z:

При совершении обратного БПФ получается решение на следующем расстоянии z + Δz от источника:

Далее рассмотрим эффект термовязкого поглощения, для которого уравнение записывается в виде:

В спектральном представлении данное уравнение имеет точное аналитическое решение:

Нелинейные эффекты описываются дифференциальным уравнением:

Так как акустическое давление представлено в виде ряда Фурье по временным гармоникам (2), то уравнение (10) в данной точке пространства запишется в виде системы нелинейных связанных уравнений [10]:

где $p_{n}^{*}$ – комплексно-сопряженная амплитуда гармоники. Таким образом, для нахождения поля на следующем шаге $\Delta z$ по оси z необходимо решить систему обыкновенных дифференциальных уравнений первого порядка для амплитуд гармоник, которая может быть поставлена как задача Коши:

Здесь вектор значений $\vec {y}$ размера N_max представляет набор гармоник в каждой точке пространства, а $\vec {f}$ – функция от амплитуд гармоник, стоящая в правой части уравнения (10). Приближенное решение системы на следующем m + 1 шаге строится методом Рунге–Кутты четвертого порядка точности [10]:

Вычисления повторяются в цикле до прохождения необходимого интервала по оси z. При этом используется метод расщепления по физическим факторам второго порядка точности [13]. Это означает, что на каждом шаге цикла сначала выполняется расчет операторов дифракции и поглощения на шаге ${{\Delta z} \mathord{\left/ {\vphantom {{\Delta z} 2}} \right. \kern-0em} 2},$ далее вычисляется оператор нелинейности на полном шаге $\Delta z,$ и снова повторяется расчет для первых двух операторов на половине шага.

Расчеты были проведены на CPU Intel Core i7 4790 (4 физических ядра и 8 виртуальных ядер) и на GPU видеокарты Nvidia GTX1070, для чего была написана программа на языке C, содержащая функции ядра CUDA, которые реализовали алгоритмы (6), (9) и (13) соответственно. Двумерные фурье-преобразования, выполнение которых необходимо при использовании метода углового спектра, проводились с помощью встроенной библиотеки cuFFT из пакета Сuda Development Toolkit. Параллельное исполнение здесь достигается как за счет внутреннего параллелизма алгоритма быстрого преобразования Фурье, реализованного для GPU, так и за счет выполнения функции ядра CUDA при умножении пространственного спектра на пропагатор (6). Распараллеливание алгоритмов поглощения и нелинейности производилось по пространственным координатам плоскости xy. На многоядерном процессоре ядра выполняли параллельно вычисления операторов поглощения и нелинейности для различных пространственных точек в плоскости xy. В алгоритме для CPU параллельный расчет дифракции достигался за счет одновременной обработки ядрами CPU полей нескольких гармоник по алгоритму (5)–(7).

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

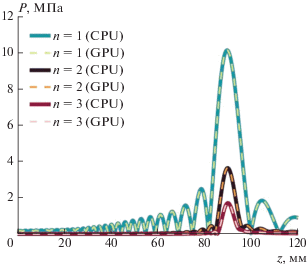
Начальное распределение комплексной амплитуды первой гармоники в плоскости z = 0 было получено при помощи интеграла Рэлея [14], рассчитанного для фокусированного преобразователя с частотой 1 МГц, диаметром 10 см и с фокусным расстоянием 9 см [12]. Распределение задавалось на квадратной сетке с общим числом ячеек N_xN_y, где N_x = N_y = 2560, с пространственными шагами Δx = Δy = 0.4 мм, количество гармоник, используемых в расчете, N_max = 50. В результате работы алгоритма были получены распределения первых трех гармоник поля на оси излучателя (рис. 2), а также в фокальной (рис. 3а–3в) и осевой плоскостях (рис. 3г–3е). Рассчитанные пространственные распределения амплитуд гармоник сравнивались с распределениями, полученными в программе, реализованной на CPU. Оба расчета дали неотличимые друг от друга результаты, что подтвердило правильность реализованного для GPU алгоритма.

В табл. 1 представлено сравнение времени работы однопоточного алгоритма, реализованного на CPU, с многопоточными алгоритмами для CPU и с алгоритмом для GPU при распространении пучка на 1200 шагов (или на 120 мм). Благодаря использованию GPU можно примерно на порядок ускорить расчеты по сравнению с 8-поточным алгоритмом для CPU, хотя ядер на графическом процессоре в сотни раз больше. Это связано с различием мощностей ядер процессоров, а также со временем, затраченным на обмен данными между CPU и GPU. Обратим внимание на скорость вычислений на GPU по сравнению со скоростью вычислений на 8 потоках CPU для различного числа гармоник (табл. 2). Видно, что ускорение растет пропорционально увеличению количества гармоник. В силу того, что вычисления в обоих алгоритмах основаны на наборе простейших арифметических операций для большого объема данных, алгоритм для GPU выполняется быстрее за счет большего количества параллельных потоков, несмотря на меньшую мощность ядер данного процессора. Поэтому ускорение растет при увеличении объема данных, например, за счет увеличения числа гармоник.

ЗАКЛЮЧЕНИЕ

Продемонстрировано применение вычислений на графических процессорах для распараллеливания алгоритма решения уравнения Вестервельта на примере расчета поля, создаваемого фокусирующим ультразвуковым излучателем. Реализованная версия алгоритма для GPU позволила ускорить вычисления по сравнению с алгоритмом для CPU на порядок. Планируется дальнейшая оптимизация алгоритма для GPU для большего ускорения вычислений.

Работа выполнена при поддержке РФФИ (проект № 20-32-70142).