1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 85, № 6, 2021

Известия РАН. Серия физическая, 2021, T. 85, № 6, стр. 889-894

Применение параметрического моделирования случайных процессов для определения потерь в линейных колебательных системах

И. А. Карпов 1, *, А. С. Гребенников 1, А. А. Ким 1

1 Федеральное государственное бюджетное учреждение науки Институт машиноведения имени А.А. Благонравова Российской академии наук
Москва, Россия

* E-mail: karpov@imash.ac.ru

Поступила в редакцию 09.12.2020
После доработки 25.01.2021
Принята к публикации 26.02.2021

Полный текст (PDF)

Аннотация

Предложен новый метод определения потерь в акустических средах, основанный на параметрическом моделировании измеренных случайных вибрационных или акустических колебаний. Метод апробирован в лабораторном эксперименте, показана его работоспособность и перспективность.

ВВЕДЕНИЕ

Данная работа относится к области акустики, которая формулируется как “экспериментальная идентификация параметров колебательных систем” [1], и направлена на решение одной из ее задач – экспериментальное определение количества демпфирования (потерь) в вибрационных и акустических системах.

Экспериментальная идентификация параметров необходима для проверки и построения адекватных математических моделей колебательных систем, способных верно прогнозировать колебания систем и решать с их помощью практические задачи. Эта область акустики развивается уже более полувека, и в ней получено немало полезных научных и прикладных результатов [1]. Однако в ней еще остается ряд не до конца решенных проблем. Одна из них – это определение с приемлемой точностью параметров, характеризующих потери колебательной энергии из-за вязкого и сухого трения, излучения и рассеяния звука, нелинейных эффектов и других трудно контролируемых причин. Теория пока не может рассчитывать эти параметры с нужной точностью [2], а экспериментальные методы [1, 3–7] могут обеспечить их измерение лишь при определенных условиях и ограничениях на величину коэффициента потерь. Между тем создание современных эффективных средств снижения шума и вибраций, в частности, акустических метаматериалов, требует знания точных величин демпфирования виброакустических систем и умения ими управлять [8]. Поэтому разработка простого и надежного метода для экспериментального определения коэффициента потерь в широком динамическом диапазоне и с высокой точностью – актуальная задача современной акустики.

Данная задача решается с помощью параметрических моделей авторегрессии и скользящего среднего (АРСС-моделей или ARMA-models) дискретно-временных случайных процессов (какими в большинстве своем и являются акустические и вибрационные сигналы технических источников). Параметрические методы с АРСС-моделями разрабатывались и применялись первоначально в тех областях науки, где требуется прогнозирование и управление случайными процессами – в экономике, управлении производственными процессами, затем в теории автоматического регулирования [9], а с конца прошлого века и в технической акустике, особенно в задачах виброакустической диагностики и мониторинга изделий машиностроения и строительства, включая задачу идентификации их модальных параметров [10–14]. Однако систематического и целенаправленного исследования возможностей, особенностей и ограничений метода идентификации потерь в виброакустических системах с помощью АРСС-моделей никто не проводил.

В первой нашей работе [15] такая задача была сформулирована и рассмотрена на основе авторегрессионной АР-модели, был построен новый алгоритм идентификации потерь, учитывающий специфику виброакустических систем и отличающийся от известных алгоритмов, в частности, от алгоритма Юла–Уолкера [16] использованием возбуждающих случайных сигналов с конечной полосой рабочих частот; алгоритм был успешно опробован и отработан на искусственных сигналах в компьютерном эксперименте.

В представленном исследовании, являющемся продолжением статьи [15], основное содержание составляют результаты лабораторного эксперимента, проведенного авторами с целью проверки работоспособности предложенного метода на двух реальных колебательных системах и оценки его точности. Сопоставление с результатами, полученными в этом же эксперименте одним из классических методов на основе спектрального анализа, показало, что параметрический метод не уступает классическому по точности идентификации потерь и превосходит его по экономичности (для получения результата ему требуется существенно меньше данных измерения). Тем самым экспериментально подтверждена работоспособность предложенного параметрического метода идентификации потерь колебательных систем и показана перспективность его использования в измерительной практике.

ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ

Эксперимент проводился на вибрационной установке, состоящей из электродинамического вибростенда и его системы управления. Функциональная схема установки представлена на рис. 1.

Рис. 1.

Функциональная схема экспериментальной установки.

Исполнительным элементом виброустановки является электродинамический вибростенд, на рабочем столе которого закрепляется оснастка с исследуемым образцом. Система управления вибростендом представляет собой программно-аппаратный комплекс, реализованный на основе персонального компьютера. Аппаратная часть комплекса содержит два акселерометра B&K Type 4393, блок согласования сигналов – усилитель NEXUS, устройство генерации и сбора динамических сигналов NI USB-4431 и управляющий компьютер. Включение в состав системы управления устройства NI USB-4431 позволяет использовать компьютер одновременно как для генерации, так и для регистрации сигналов.

Специализированное программное обеспечение системы управления – это разработанный в среде MATLAB пакет программ для генерации, сбора, обработки и визуализации данных.

В эксперименте исследовались два образца в виде простейших механических колебательных систем-осцилляторов, отличающихся своей добротностью (рис. 2).

Рис. 2.

Образец 1 (а) и образец 2 (б).

Образец 1 с низкой добротностью (Q < 10) состоит из слоя резины и массы (рис. 2а). Образец 2 (Q > 40) был выполнен в виде массы, закрепленной на специально спроектированной стальной задемпфированной пластине (рис. 2б).

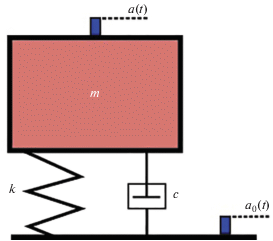
Два акселерометра измеряли ускорение массы осциллятора a(t) и вибростола a0(t) – см. рис. 3. Задача состояла в определении по этим данным коэффициента потерь осцилляторов двумя методами – классическим и параметрическим, и в сравнении этих двух методов.

Рис. 3.

Расчетная модель образца.

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ПОТЕРЬ КЛАССИЧЕСКИМ И ПАРАМЕТРИЧЕСКИМ МЕТОДАМИ

При определении коэффициента потерь одним из классических методов [1] стенд возбуждался гармоническим сигналом переменной частоты и с постоянной амплитудой ускорения a0 = = 3 м ⋅ с–2. По измеренному сигналу a(t) строилась амплитудно-частотная характеристика (АЧХ), коэффициент потерь рассчитывался по ширине резонансной кривой.

(1)
$\eta = \frac{{\Delta f}}{{{{f}_{0}}}},$
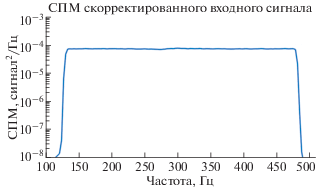
где f0 – собственная частота осциллятора. Измерения дали следующие значения для собственных частот и коэффициента потерь – см. табл. 1.

Таблица 1.  

Модальные параметры, определенные классическим методом

  Собственная частота f0, Гц Коэффициент потерь $\eta $
Образец 1 (рис. 2а) 280.7 0.0958
Образец 2 (рис. 2б) 401.2 0.0223

При определении коэффициента потерь параметрическим методом стенд возбуждался случайным шумом a0(t). a0(t) – это гауссов сигнал, с постоянной спектральной плотностью мощности (СПМ) в полосе частот, содержащей собственную частоту резонатора (пример такого сигнала см. на рис. 4). В качестве параметрической модели ускорения a(t) использовалась авторегрессионая модель скользящего среднего x[n]

(2)
$\begin{gathered} x\left[ n \right] = - {{a}_{1}}x\left[ {n - 1} \right] - {{a}_{2}}x[n - 2] + {{b}_{0}}w\left[ n \right] + \\ + \,\,{{b}_{1}}w\left[ {n - 1} \right], \\ \end{gathered} $
Рис. 4.

Спектральная плотность мощности случайного сигнала возбуждения a0(t).

с четырьмя неизвестными параметрами a1, a2, b0, b1 (обоснование выбора см. далее). Для удобства для сигналов a(t) и a0(t) введены принятые в литературе стандартные обозначения x(t) и w(t). В развернутом виде это система линейных алгебраических уравнений с четырьмя неизвестными:

(3)
$\begin{gathered} \left[ {\begin{array}{*{20}{c}} {x\left[ 2 \right]}&{x\left[ 1 \right]}&{ - w\left[ 3 \right]}&{ - w\left[ 2 \right]} \\ {x\left[ 3 \right]}&{x\left[ 2 \right]}&{ - w\left[ 4 \right]}&{ - w\left[ 3 \right]} \\ {x\left[ 4 \right]}&{x\left[ 3 \right]}&{ - w\left[ 5 \right]}&{ - w\left[ 4 \right]} \\ \vdots & \vdots & \vdots & \vdots \\ {x\left[ {N - 1} \right]}&{x\left[ {N - 2} \right]}&{ - w\left[ N \right]}&{ - w\left[ {N - 1} \right]} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{a}_{1}}} \\ {{{a}_{2}}} \\ {{{b}_{0}}} \\ {{{b}_{1}}} \end{array}} \right] = \\ = - \left[ {\begin{array}{*{20}{c}} {x\left[ 3 \right]} \\ {x\left[ 4 \right]} \\ {x\left[ 5 \right]} \\ \vdots \\ {x\left[ N \right]} \end{array}} \right]\,\,\,\,{\text{или}}\,\,\,\,{\mathbf{{\rm Z}}}d = {{x}_{1}}, \\ \end{gathered} $
где $d = {{\left[ {\begin{array}{*{20}{c}} {{{a}_{1}}}&{{{a}_{2}}}&{{{b}_{0}}}&{{{b}_{1}}} \end{array}} \right]}^{T}}$ – искомый вектор. Будем искать решение d из условия минимума квадратичной невязки $\left\{ {{{{\left( {{\mathbf{Z}}d - {{x}_{1}}} \right)}}^{T}}\left( {{\mathbf{Z}}d - {{x}_{1}}} \right) \to \min } \right\}{\text{:}}$

(4)
$\begin{gathered} \frac{\partial }{{\partial {{d}^{Т}}}}{{\left( {{\mathbf{Z}}d - {{x}_{1}}} \right)}^{T}}\left( {{\mathbf{Z}}d - {{x}_{1}}} \right) = \\ = \,\,0 \Rightarrow {{{\mathbf{Z}}}^{Т}}{\mathbf{Z}}d - {{{\mathbf{Z}}}^{Т}}{{x}_{1}} = 0. \\ \end{gathered} $

Таким образом получено, что d можно найти из уравнения:

(5)
$d = {{\left( {{{{\mathbf{Z}}}^{Т}}{\mathbf{Z}}} \right)}^{{ - 1}}}{{{\mathbf{Z}}}^{Т}}{{x}_{1}}.$

Отсюда по АР-модели второго порядка с помощью формул, полученных в статье [15], можно найти искомые собственную частоту f0 и коэффициент потерь $\eta {\text{:}}$

(6)
$\begin{gathered} \eta = \frac{{ - 1}}{{2\pi {{f}_{0}}T}}\ln \left( {{{a}_{2}}} \right);\,\,\,\,{{f}_{0}} = \\ = \sqrt {\frac{1}{{{{{\left( {2\pi T} \right)}}^{2}}}}\left( {\frac{{{{{\left( {\ln \left( {{{a}_{2}}} \right)} \right)}}^{2}}}}{4} + {{{\left( {\arccos \left[ {\frac{{ - {{a}_{1}}}}{{2\sqrt {{{a}_{2}}} }}} \right]} \right)}}^{2}}} \right)} . \\ \end{gathered} $

Выбор количества параметров скользящего среднего был сделан из следующих соображений. Если написать уравнение колебаний для системы, изображенной на рис. 3:

(7)
$m\ddot {x}\left( t \right) + c\left( {\dot {x}\left( t \right) - {{{\dot {x}}}_{0}}\left( t \right)} \right) + k\left( {x\left( t \right) - {{x}_{0}}\left( t \right)} \right) = 0,$
где $x$, x0 – смещение массы и стола, и подставить в это уравнение формулы конечных разностей

(8)
$\begin{gathered} \dot {y}\left( {nT} \right) \cong \frac{{y\left( {nT} \right) - y\left( {\left( {n - 1} \right)T} \right)}}{T};\,\,\,\,\ddot {y}\left( {nT} \right) \cong \\ \cong \frac{{y\left( {nT} \right) - 2y\left( {\left( {n - 1} \right)T} \right) + y\left( {\left( {n - 2} \right)T} \right)}}{{{{T}^{2}}}}, \\ \end{gathered} $

то видно, что получившееся уравнение можно свести к виду АРСС-модели с p = 2 и q = 2, то есть к уравнению с четырьмя параметрами. Здесь T = Fs–1, Fs – частота дискретизации.

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ПОТЕРЬ ПАРАМЕТРИЧЕСКИМ МЕТОДОМ В ОБЩЕМ СЛУЧАЕ

Для исследования более сложных систем следует использовать следующую общую АРСС-модель в виде конечно-разностного уравнения, позволяющую вычислять члены дискретно-временного ряда по его предыдущим значениям [9]:

(9)
$x\left[ n \right] = - \sum\limits_{j = 1}^p {{{a}_{j}}x\left[ {n - j} \right]} + \sum\limits_{j = 0}^{q - 1} {{{b}_{j}}w\left[ {n - j} \right]} ,$
где p и q – количество параметров авторегрессии (АР) и скользящего среднего (СС), и составить следующие матрицы:
(10)
$\begin{gathered} {\mathbf{Z}}d = {{x}_{1}},\,\,\,\,{\text{где}}\,\,\,\,{\mathbf{Z}} = \\ = \left[ {\begin{array}{*{20}{c}} {x\left[ l \right]}&{x\left[ {l - 1} \right]}& \vdots &{x\left[ {l - p + 1} \right]}&{ - w\left[ {l + 1} \right]}&{ - w\left[ l \right]}& \vdots &{ - w\left[ {l - q + 2} \right]} \\ {x\left[ {l + 1} \right]}&{x\left[ l \right]}& \vdots &{x\left[ {l - p + 2} \right]}&{ - w\left[ {l + 2} \right]}&{ - w\left[ {l + 1} \right]}& \vdots &{ - w\left[ {l - q + 3} \right]} \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ {x\left[ {N - 1} \right]}&{x\left[ {N - 2} \right]}& \vdots &{x\left[ {N - p} \right]}&{ - w\left[ N \right]}&{w\left[ {N - 1} \right]}& \vdots &{w\left[ {N - q + 1} \right]} \end{array}} \right]; \\ d = {{\left[ {\begin{array}{*{20}{c}} {{{a}_{1}}}&{{{a}_{2}}}& \ldots &{{{a}_{p}}}&{{{b}_{0}}}&{{{b}_{1}}}& \ldots &{{{b}_{{q - 1}}}} \end{array}} \right]}^{T}}; \\ {{x}_{1}} = - {{\left[ {\begin{array}{*{20}{c}} {x\left[ {l + 1} \right]}&{x\left[ {l + 2} \right]}& \ldots &{x\left[ N \right]} \end{array}} \right]}^{T}}, \\ \end{gathered} $
где l – это наибольшее число из $\left\{ {p,q - 1} \right\}.$ Далее, аналогично (5), находится вектор коэффициентов d. Если исследуемая система имеет количество степеней свободы M большее двух, то удобнее находить пары собственных значений zi1 и zi2 следующей матрицы

(11)
${\mathbf{G}} = \left[ {\begin{array}{*{20}{c}} 0&1& \vdots &0&0 \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0&0& \vdots &0&1 \\ { - {{a}_{{2M}}}}&{ - {{a}_{{2M - 1}}}}& \vdots &{ - {{a}_{2}}}&{ - {{a}_{1}}} \end{array}} \right],$

а по ним искомые параметры:

(12)
$\begin{gathered} {\text{если}}\,\,\,\,{{z}_{{i1}}} + {{z}_{{i2}}} \geqslant 0 \\ \left\{ \begin{gathered} {{\omega }_{i}} = \sqrt {\frac{1}{{4{{T}^{2}}}}{{{\left[ {\ln \left( {{{z}_{{i1}}}{{z}_{{i2}}}} \right)} \right]}}^{2}} + {{{\left( {\frac{1}{T}{\text{arctg}}\left| {\frac{{{{z}_{{i1}}} - {{z}_{{i2}}}}}{{{{z}_{{i1}}} + {{z}_{{i2}}}}}} \right|} \right)}}^{2}}} \hfill \\ {{\eta }_{i}} = - \frac{1}{{T{{\omega }_{i}}}}\ln \left[ {{{z}_{{i1}}}{{z}_{{i2}}}} \right] \hfill \\ \end{gathered} \right., \\ {\text{если}}\,\,\,\,{{z}_{{i1}}} + {{z}_{{i2}}} < 0 \\ \left\{ \begin{gathered} {{\omega }_{i}} = \sqrt {\frac{1}{{4{{T}^{2}}}}{{{\left[ {\ln \left( {{{z}_{{i1}}}{{z}_{{i2}}}} \right)} \right]}}^{2}} + {{{\left[ {\frac{1}{T}\left( {\pi - {\text{arctg}}\left| {\frac{{{{z}_{{i1}}} - {{z}_{{i2}}}}}{{{{z}_{{i1}}} + {{z}_{{i2}}}}}} \right|} \right)} \right]}}^{2}}} \hfill \\ {{\eta }_{i}} = - \frac{1}{{T{{\omega }_{i}}}}\ln \left[ {{{z}_{{i1}}}{{z}_{{i2}}}} \right] \hfill \\ \end{gathered} \right.. \\ \end{gathered} $

ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Результаты определения собственных частот и коэффициента потерь параметрическим методом представлены в табл. 2.

Таблица 2.  

Модальные параметры, определенные параметрическим методом

  Собственная частота f0 (Гц) и отличие от результата таблицы 1 Коэффициент потерь $\eta $ и отличие от значений таблицы 1
Образец 1 (рис. 2а) 277.7 1.1% 0.0966 0.9%
Образец 2 (рис. 2б) 398.1 0.8% 0.0225 1%

Сравнение этих результатов с результатами, полученными классическим методом (табл. 1), показывает, что разница между ними невелика (порядка одного процента). По точности результатов эти два метода, таким образом, сравнимы.

Однако по другим критериям они отличаются значительно, особенно по времени измерения и объема необходимых данных измерения. Исследования классическими методами, связанные со спектральным анализом, требуют измерения длинных реализаций сигналов, в то время как для параметрического метода достаточно коротких реализаций. Например, в частотном диапазоне проведенного эксперимента для классического метода требовались записи сигналов продолжительностью в несколько минут, в то время как для параметрического метода достаточно было записей сигналов длиной в доли секунды (<0.5 с).

ЗАКЛЮЧЕНИЕ

Предложен метод экспериментального определения коэффициента потерь колебательной системы с помощью параметрического АРСС-моделирования. Проведен лабораторный эксперимент, подтвердивший работоспособность и перспективность метода.

Список литературы

  1. Ewins D.J. Modal testing: theory and practice. Letchworth: Research Studies Press, 1986. 356 p.

  2. Нашиф А., Джоунс Д., Хендерсон Дж. Демпфирование колебаний. М.: Мир, 1988. 448 с.

  3. McConnell K.G. Vibration testing: theory and practice. N.Y.: John Wiley, 1995. 320 p.

  4. Heylen W., Lammens S., Sas P. Modal analysis: theory and practice. Leuven: Katholic University, 1997. 492 p.

  5. Trivett D.H., Robinson A.Z. // J. Acoust. Soc. Amer. 1981. V. 70. P. 1166.

  6. Hua Y., Sarkar T.K. // IEEE Trans. Acoust. Speech. Signal Proc. 1990. V. 38. P. 1272.

  7. Liu K. // J. Sound Vib. 1996. V. 197. No. 4. P. 387.

  8. Бобровницкий Ю.И, Томилина Т.М. // Акуст. журн. 2018. Т. 64. № 5. С. 517; Bobrovnitskii Y.I., Tomilina T.M. // Acoust. Phys. 2018. V. 64. No. 5. P. 519.

  9. Бокс Дж., Дженкинс Г.Д. Анализ временных рядов. Прогноз и управление. М.: Мир, 1974. 604 с.

  10. Spiridonakos M.D., Fassois S.D. // Mech. Syst. Signal Proc. 2014. V. 47. P. 175.

  11. Pi Y.L., Mickleborough N.C. // J. Eng. Mech. 1989. V. 115. P. 2232.

  12. Gautier P.-E., Gontier C., Small M. // J. Sound Vib. 1995. V. 179. P. 227.

  13. Bertha M., Galinval J.-C. // Mech. Syst. Signal Proc. 2016. V. 88. P. 166.

  14. Yang J.-H., Lam H.-F. // Mech. Syst. Signal Proc. 2019. V. 133. Art. No. 106289.

  15. Карпов И.А. // Уч. зап. физ. фак-та МГУ. 2020. № 1. C. 2011701.

  16. Марпл С.Л., мл. Цифровой спектральный анализ и его приложения. М.: Мир, 1990. 584 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал