1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 85, № 6, 2021

Известия РАН. Серия физическая, 2021, T. 85, № 6, стр. 895-900

Об оценке скорости ротационных волн в простой кубической решетке кристалла фуллерита

И. С. Павлов 1, 2, *, В. И. Ерофеев 1, А. В. Муравьева 2, А. А. Васильев 3

1 Институт проблем машиностроения РАН – филиал Федерального государственного бюджетного научного учреждения “Федеральный исследовательский центр Институт прикладной физики Российской академии наук”
Нижний Новгород, Россия

2 Федеральное государственное автономное образовательное учреждение высшего образования “Национальный исследовательский Нижегородский государственный университет имени Н.И. Лобачевского”
Нижний Новгород, Россия

3 Федеральное государственное бюджетное образовательное учреждение высшего образования “Тверской государственный университет”
Тверь, Россия

* E-mail: ispavlov@mail.ru

Поступила в редакцию 09.12.2020
После доработки 25.01.2021
Принята к публикации 26.02.2021

Полный текст (PDF)

Аннотация

Методом структурного моделирования построена трехмерная математическая модель простой кубической решетки кристалла фуллерита. Получены аналитические зависимости скоростей акустических и вращательных (ротационных) волн от параметров микроструктуры такой среды. Показано, что в зависимости от значений параметров микроструктуры скорость ротационных волн может превосходить скорость поперечных волн.

ВВЕДЕНИЕ

В настоящее время интенсивно развиваются технологии создания метаматериалов – нового класса веществ со сложно организованной внутренней структурой (микроструктурой), обладающих уникальными физико-механическими свойствами [1]. Впервые они появились в области оптики и фотоники [2], но сейчас все чаще встречаются и в других областях. Например, широко применяются акустические метаматериалы [3–7], используемые, в частности, как акустические поглотители [8].

Одним из примеров материала с уникальными физико-механическими свойствами являются фуллериты – твердотельные структуры, образованные на основе фуллеренов (как С60, так и высших фуллеренов – С70, С76, С78, С80, С82 и т.д.) [9]. Принадлежность фуллеритов к кристаллам молекулярного типа позволяет рассматривать образующие их фуллерены подобно молекулам, причем при тепловом движении они могут легко менять относительную пространственную ориентацию даже в условиях кристаллического окружения, т.е. совершать так называемые ориентационные фазовые переходы. Такая способность фуллеренов обусловлена их высокосимметричной, почти сферической формой. Смена ориентации фуллеренов происходит в том случае, когда они, совершая крутильные колебания, преодолевают определенный энергетический барьер и переходят к псевдовращению. В частности, фуллерены С60 в кристалле находятся в состоянии почти свободного вращения с тремя степенями свободы [9].

Сверх- и ультра-твердые фуллериты характеризуются уникально высокими значениями скоростей продольных упругих волн и широким диапазоном этих значений в пределах от 11 до 26 км/с в зависимости от их структуры, определяемой условиями синтеза [10]. Измеренное в одной из фуллеритовых фаз значение 26 км/с является рекордным – оно почти на 20% больше скорости продольных волн в графите вдоль атомных слоев, равной 21.6 км/с (до последнего времени это значение было наибольшим для всех известных веществ) и на 40% больше соответствующей скорости в алмазе (18.6 км/с). Скорости поперечных волн в твердых фуллеритовых фазах также высоки (их значения лежат в пределах от 7 до 9.7 км/с), но все же они меньше, чем в алмазе (11.6–12.8 км/с), которые по-прежнему остаются рекордными среди известных в настоящее время веществ.

Экспериментальные данные показывают [9], что фуллерены С60 при комнатной температуре кристаллизуются с образованием гранецентрированной кубической решетки (ГЦК) – самой плотноупакованной из кубических решеток с постоянной решетки а = 1.417 нм. Расстояние между центрами ближайших фуллеренов С60 в кристаллической структуре 1.002 нм, плотность фуллерита составляет 1.72 г/см3. При понижении температуры до 250 К, кристаллическая структура фуллерита С60 испытывает фазовое превращение первого рода, при котором ГЦК-решетка перестраивается в простую кубическую (ПК) решетку [11].

Однако создание метаматериалов и исследование протекающих в них линейных и нелинейных волновых процессов [12–14] при отсутствии адекватных математических моделей крайне затруднительно. Одним из наиболее эффективных методов построения математических моделей метаматериалов является метод структурного моделирования [15–19]. Этот метод в явном виде учитывает микроструктуру среды и позволяет строить не только дискретные, но и континуальные модели среды в различных приближениях. Микроструктура среды в таких моделях, как правило, описывается частицами конечного размера, их взаимным расположением по отношению друг к другу (т.е. структурой решетки), а также параметрами силового и моментного взаимодействия между частицами. Сами же взаимодействия обычно моделируются стержнями, балками [20, 21] или пружинами [16, 22]. В отличие от обобщенных континуумов типа среды Коссера [23], математические модели метаматериалов, построенные таким методом, позволяют не только получить представление о качественном влиянии локальной структуры на эффективные модули упругости соответствующей среды, но и проводить количественные оценки этих величин.

В данной работе методом структурного моделирования разрабатывается трехмерная математическая модель простой кубической решетки кристалла фуллерита, состоящего из сферических частиц, обладающих тремя трансляционными и тремя ротационными (вращательными) степенями свободы. В рамках такой модели удалось установить аналитические зависимости между параметрами микроструктуры и макрохарактеристиками среды и, как следствие, произвести теоретические оценки скоростей ротационных волн.

ДИСКРЕТНАЯ МОДЕЛЬ КРИСТАЛЛА ФУЛЛЕРИТА

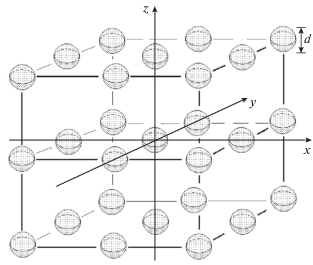
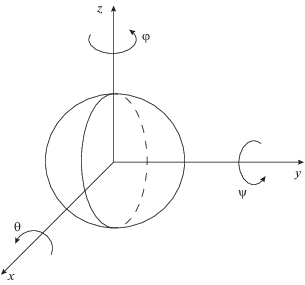
Рассмотрим кубическую решетку из жестких шарообразных частиц (зерен) массы M, имеющих форму шара диаметром d (рис. 1). В исходном состоянии они сосредоточены в узлах решетки с периодом a. Каждая частица обладает шестью степенями свободы: центр масс частицы с номером N = N(i, j, k) может смещаться вдоль осей x, y и z (трансляционные степени свободы ${{u}_{{i,j,k}}},$ ${{\nu }_{{i,j,k}}}$ и ${{w}_{{i,j,k}}}$), а сама частица может поворачиваться вокруг каждой из этих осей (ротационные степени свободы ${{\theta }_{{i,j,k}}},$ ${{\psi }_{{i,j,k}}}$ и ${{\varphi }_{{i,j,k}}}$) (рис. 2). В этом случае кинетическая энергия частицы N описывается следующей формулой:

(1)
$T = \frac{M}{2}\left( {u_{t}^{2} + \nu _{t}^{2} + w_{t}^{2}} \right) + \frac{J}{2}\left( {\varphi _{t}^{2} + \theta _{t}^{2} + \psi _{t}^{2}} \right),$
где $J = \frac{2}{5}M{{\left( {\frac{d}{2}} \right)}^{2}}$ = $\frac{1}{{10}}M{{d}^{2}}$ = $\frac{2}{5}M\frac{{3{{b}^{2}}}}{4} = 0.3M{{b}^{2}}$ – момент инерции частицы относительно каждой оси, проходящей через ее центр масс.

Рис. 1.

Трехмерная решетка из сферических частиц.

Рис. 2.

Ротационные степени свободы частицы.

Пространство между частицами представляет собой безмассовую упругую среду, через которую передаются силовые и моментные воздействия, моделируемые упругими пружинами. Считается, что частица N = N (i, j, k) взаимодействует лишь с ближайшими соседями, удаленными от нее на расстояние а (частицы 1-й координационной сферы: (i – 1, j, k), (i, j – 1, k), (i, j + 1, k), (i + 1, j, k)), $a\sqrt 2 $ (частицы 2-й координационной сферы: (i – 1, j – 1, k), (i – 1, j + 1, k), (i + 1, j – 1, k), (i + 1, j + 1, k)) и $a\sqrt 3 $ (частицы 3-й сферы: (i – 1, j – 1, k – 1), (i – 1, j – 1, k + 1), (i – 1, j + 1, k – 1), (i – 1, j + 1, k + 1), (i + 1, j – 1, k – 1), (i + 1, j – 1, k + 1), (i + 1, j + 1, k – 1), (i + 1, j + 1, k + 1)) (рис. 1).

Центральные и нецентральные взаимодействия соседних частиц моделируются упругими пружинами пяти типов: центральными (с жесткостью K0), нецентральными с жесткостью K1 (рис. 3), диагональными (K2), а также пружинами с жесткостями K3 и K4, соединяющими центральную частицу с зернами, соответственно, второй и третьей координационных сфер. Центральные пружины K0 соединяют центры соседних частиц, точки соединения с частицами пружин вида K1 и K2 лежат в вершинах куба со стороной b, вписанного в шар диаметра $d = b\sqrt 3 $ (на рис. 3 ${{{\text{A}}}_{{\text{2}}}}{\text{B}}_{1}^{'},$ ${{{\text{B}}}_{{\text{2}}}}{\text{A}}_{1}^{'},$ ${{{\text{E}}}_{{\text{2}}}}{\text{C}}_{1}^{'},$ ${{{\text{C}}}_{{\text{2}}}}{\text{E}}_{1}^{'}$ – пружины с жесткостью K1, ${{{\text{A}}}_{{\text{2}}}}{\text{C}}_{1}^{'},$ ${{{\text{E}}}_{{\text{2}}}}{\text{B}}_{1}^{'},$ ${{{\text{B}}}_{{\text{2}}}}{\text{E}}_{1}^{'},$ ${{{\text{C}}}_{{\text{2}}}}{\text{A}}_{1}^{'}$ – пружины вида K2), а пружины с жесткостями K3 и K4 прикреплены к серединам ближайших друг к другу ребер кубов, геометрические центры которых в исходном состоянии расположены на расстояниях $a\sqrt 2 $ и $a\sqrt 3 .$

Рис. 3.

Схема силовых взаимодействий между ближайшими соседями по решетке (частицами первой координационной сферы).

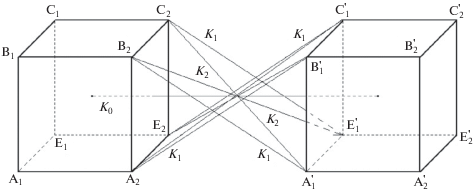
Пружины с жесткостями K0, K1, K2 и K3 описывают взаимодействия частиц внутри одного слоя. Так, центральные (K0) и нецентральные (K1) пружины характеризуют взаимодействия при растяжении–сжатии материала. Через пружины K1 передаются также моменты при поворотах частиц. Пружины с жесткостью K1 и K2 характеризуют силовые взаимодействия частиц при сдвиговых деформациях в материале. Заметим, что выбранная схема силовых взаимодействий внутри одного слоя аналогична введенной в двумерной решетке из круглых частиц [17].

Предполагается, что смещения зерен малы по сравнению с размерами элементарной ячейки рассматриваемой решетки. Взаимодействие частиц при отклонениях от положения равновесия определяется относительными удлинениями пружин. Потенциальная энергия, обусловленная взаимодействием частицы N c восемью ближайшими соседями по решетке, описывается формулой

(2)
$\begin{gathered} {{U}_{N}} = \frac{1}{2}\left( {\sum\limits_{n = 1}^4 {\frac{{{{K}_{0}}}}{2}D_{{0n}}^{2}} + \sum\limits_{n = 1}^{16} {\frac{{{{K}_{1}}}}{2}D_{{1n}}^{2}} + \sum\limits_{n = 1}^{16} {\frac{{{{K}_{2}}}}{2}D_{{2n}}^{2}} + } \right. \\ \left. { + \,\,\sum\limits_{n = 1}^4 {\frac{{{{K}_{3}}}}{2}D_{{3n}}^{2}} + \sum\limits_{n = 1}^4 {\frac{{{{K}_{4}}}}{2}D_{{4n}}^{2}} } \right), \\ \end{gathered} $
где Dln (l = 0, 1, 2, 3, 4) – удлинения пронумерованных в произвольном порядке пружин пяти типов, соединяющих частицу с ее соседями. Эти удлинения определяются изменениями расстояний между точками соединения соответствующих пружин (рис. 3). Далее от полученной дискретной модели перейдем в континуальное приближение. Для этого выразим удлинения пружин через смещения и углы поворотов частиц и разложим последние в ряд Тейлора до квадратичных членов.

КОНТИНУАЛЬНАЯ МОДЕЛЬ КРИСТАЛЛА ФУЛЛЕРИТА

В случае длинноволновых возмущений, когда λ $ \gg $ a функция Лагранжа L рассматриваемой среды из сферических частиц с точностью до квадратичных слагаемых примет вид:

(3)
$\begin{gathered} L = \frac{M}{2}\left( {u_{t}^{2} + \nu _{t}^{2} + w_{t}^{2}} \right) + \frac{J}{2}\left( {\varphi _{t}^{2} + \theta _{t}^{2} + \psi _{t}^{2}} \right) - \\ - \,\,\frac{M}{2}\left[ {c_{1}^{2}\left( {u_{x}^{2} + \nu _{y}^{2} + w_{z}^{2}} \right) + c_{2}^{2}\left( {\nu _{x}^{2} + \nu _{z}^{2} + u_{y}^{2} + u_{z}^{2} + } \right.} \right. \\ \left. { + \,\,w_{x}^{2} + w_{y}^{2}} \right) + {{s}^{2}}({{\nu }_{y}}{{w}_{z}} + {{\nu }_{z}}{{w}_{y}} + {{u}_{x}}{{w}_{z}} + {{u}_{z}}{{w}_{x}} + \\ + \,\,{{u}_{x}}{{\nu }_{y}} + {{u}_{y}}{{\nu }_{x}}) + \beta _{1}^{2}({{\varphi }^{2}} + {{\theta }^{2}} + {{\psi }^{2}}) + \\ + \,\,\beta _{2}^{2}({{\nu }_{x}}\varphi - {{w}_{x}}\psi + {{w}_{y}}\theta - {{u}_{y}}\varphi + {{u}_{z}}\psi - {{\nu }_{z}}\theta ) + \\ + \,\,{{b}^{2}}c_{3}^{2}\left( {\varphi _{z}^{2} + \theta _{x}^{2} + \psi _{y}^{2}} \right) + \\ + \,\,{{b}^{2}}c_{4}^{2}\left( {\varphi _{x}^{2} + \varphi _{y}^{2} + \theta _{y}^{2} + \theta _{z}^{2} + } \right.\left. {\left. {\psi _{x}^{2} + \psi _{z}^{2}} \right)} \right]. \\ \end{gathered} $

Здесь введены обозначения: ci (i = 1–4) – характерные скорости распространения соответственно продольной, поперечной и ротационных волн, s – коэффициент связи между продольными и сдвиговыми деформациями, β1 и β2 – параметры связи микроповоротов с поперечной и продольной волнами.

С помощью вариационного принципа Гамильтона–Остроградского из функции Лагранжа (3) получена система дифференциальных уравнений, описывающая распространение акустических и ротационных волн в кубической решетке из сферических частиц:

(4)
$\begin{gathered} {{u}_{{tt}}} - с_{1}^{2}{{u}_{{xx}}} - с_{2}^{2}\left( {{{u}_{{yy}}} + {{u}_{{zz}}}} \right) - {{s}^{2}}\left( {{{\nu }_{{xy}}} + {{w}_{{xz}}}} \right) + \\ + \,\,\frac{{\beta _{2}^{2}}}{2}\left( {{{\varphi }_{y}} - {{\psi }_{z}}} \right) = 0, \\ {{\nu }_{{tt}}} - с_{1}^{2}{{\nu }_{{yy}}} - с_{2}^{2}\left( {{{\nu }_{{xx}}} + {{\nu }_{{zz}}}} \right) - \\ - \,\,{{s}^{2}}\left( {{{u}_{{xy}}} + {{w}_{{yz}}}} \right) + \frac{{\beta _{2}^{2}}}{2}\left( {{{\theta }_{z}} - {{\varphi }_{x}}} \right) = 0, \\ {{w}_{{tt}}} - с_{1}^{2}{{w}_{{zz}}} - с_{2}^{2}\left( {{{w}_{{xx}}} + {{w}_{{yy}}}} \right) - {{s}^{2}}({{u}_{{xz}}} + {{\nu }_{{yz}}}) + \\ + \,\,\frac{{\beta _{2}^{2}}}{2}\left( {{{\psi }_{x}} - {{\theta }_{y}}} \right) = 0, \\ {{\theta }_{{tt}}} - c_{3}^{2}{{\theta }_{{xx}}} - с_{4}^{2}\left( {{{\theta }_{{yy}}} + {{\theta }_{{zz}}}} \right) + \\ + \,\,\frac{{\beta _{2}^{2}}}{{2J}}\left( {{{w}_{y}} - {{\nu }_{z}}} \right) + \frac{{\beta _{1}^{2}}}{J}\theta = 0, \\ {{\psi }_{{tt}}} - c_{3}^{2}{{\psi }_{{yy}}} - \,\,c_{4}^{2}\left( {{{\psi }_{{xx}}} + {{\psi }_{{zz}}}} \right) + \frac{{\beta _{2}^{2}}}{{2J}}\left( {{{u}_{z}} - {{w}_{x}}} \right) + \frac{{\beta _{1}^{2}}}{J}\psi = 0, \\ {{\varphi }_{{tt}}} - c_{3}^{2}{{\varphi }_{{zz}}} - c_{4}^{2}\left( {{{\varphi }_{{xx}}} + {{\varphi }_{{yy}}}} \right) + \\ + \,\,\frac{{\beta _{2}^{2}}}{{2J}}\left( {{{\nu }_{x}} - {{u}_{y}}} \right) + \frac{{\beta _{1}^{2}}}{J}\varphi = 0. \\ \end{gathered} $

Система (4) аналогична уравнениям динамики континуума Коссера, состоящего из центрально-симметричных частиц с тремя трансляционными и тремя ротационными степенями свободы [24]. Отличия наблюдаются лишь в коэффициентах. Коэффициенты уравнений системы (4), т.е. макропараметры среды, выражаются через силовые постоянные K0, K1, K2, K3, K4, период решетки a и размер частицы $b = {d \mathord{\left/ {\vphantom {d {2\sqrt 3 }}} \right. \kern-0em} {2\sqrt 3 }}$ следующим образом:

(5)
$\begin{gathered} c_{1}^{2} = \frac{1}{{a\rho }}\left( {{{K}_{0}} + \frac{{8{{{(a - b)}}^{2}}}}{{{{{(a - b)}}^{2}} + {{b}^{2}}}}{{K}_{1}} + \frac{{4{{{(a - b)}}^{2}}}}{{{{{(a - b)}}^{2}} + 2{{b}^{2}}}}} \right. \times \\ \left. { \times \,\,{{K}_{2}} + \frac{{{{K}_{3}}}}{{\sqrt 2 }} + \frac{{2{{K}_{4}}}}{3}} \right), \\ c_{2}^{2} = \frac{1}{{a\rho }}\left( {\frac{{4{{b}^{2}}}}{{{{{(a - b)}}^{2}} + {{b}^{2}}}}{{K}_{1}} + } \right. \\ \left. { + \,\,\frac{{4{{b}^{2}}}}{{{{{(a - b)}}^{2}} + 2{{b}^{2}}}}{{K}_{2}} + \frac{{{{K}_{3}}}}{{2\sqrt 2 }} + \frac{{2{{K}_{4}}}}{3}} \right), \\ {{s}^{2}} = \frac{1}{{a\rho }}\left( {\frac{{{{K}_{3}}}}{{\sqrt 2 }} + \frac{{4{{K}_{4}}}}{3}} \right), \\ \beta _{1}^{2} = \frac{{8{{b}^{2}}}}{{a\rho }}\left( {\frac{{{{K}_{1}}}}{{{{{(a - b)}}^{2}} + {{b}^{2}}}} + } \right.\left. {\frac{{{{K}_{2}}}}{{{{{(a - b)}}^{2}} + 2{{b}^{2}}}}} \right), \\ \beta _{2}^{2} = \frac{{8{{b}^{2}}}}{{a\rho }}\left( {\frac{{{{K}_{2}}}}{{{{{(a - b)}}^{2}} + 2{{b}^{2}}}}} \right), \\ c_{3}^{2} = \frac{{2{{b}^{2}}}}{{a\rho }}\left( {\frac{{{{K}_{1}}}}{{{{{(a - b)}}^{2}} + {{b}^{2}}}}} \right), \\ c_{4}^{2} = \frac{1}{{a\rho }}\left( {\frac{{{{K}_{1}}({{a}^{2}} + {{{(a - b)}}^{2}})}}{{{{{(a - b)}}^{2}} + {{b}^{2}}}} + \frac{{{{K}_{2}}{{a}^{2}}}}{{{{{(a - b)}}^{2}} + 2{{b}^{2}}}}} \right). \\ \end{gathered} $
Здесь $\rho = {M \mathord{\left/ {\vphantom {M {{{a}^{3}}}}} \right. \kern-0em} {{{a}^{3}}}}$ – плотность рассматриваемой среды. Из (5) следует

$\beta _{1}^{2} + {{s}^{2}} = 2c_{2}^{2},\,\,\,\,\beta _{2}^{2} + 4с_{3}^{2} = \beta _{1}^{2}.$(6)

Таким образом, в данной анизотропной среде имеется лишь 5 независимых макроконстант, причем при переходе к изотропной среде (в этом случае $с_{1}^{2} = c_{2}^{2} + {{s}^{2}}$) останется лишь 4 константы. Данная среда становится изотропной при выполнении следующего соотношения:

(7)
$\begin{gathered} {{K}_{0}} = \frac{{4{{b}^{2}} - 8{{{(a - b)}}^{2}}}}{{{{{(a - b)}}^{2}} + {{b}^{2}}}}{{K}_{1}} + \frac{{4a(2b - a)}}{{{{{(a - b)}}^{2}} + 2{{b}^{2}}}}{{K}_{2}} - \\ - \,\,\frac{{{{K}_{3}}}}{{4\sqrt 2 }} + \frac{4}{3}{{K}_{4}}. \\ \end{gathered} $

В данной модели ${{\beta }_{2}} \equiv 0$ при отсутствии пружин K2, в результате чего исчезает связь между трансляционными и ротационными степенями свободы частиц в линейном приближении, присутствующая в континууме Коссера. Если K1 = 0, то ${{с}_{3}} \equiv 0,$ в то время как в континууме Коссера этот коэффициент является ненулевым. Введение центральных пружин (с жесткостью K0) обеспечивает превосходство скорости продольных волн над скоростями остальных волн. Пружины K3 и K4 кажутся, на первый взгляд, дублирующими друг друга. Однако, как следует из формул (5), пружины этих двух типов в количественном отношении по-разному влияют на параметры ${{с}_{1}},$ ${{с}_{2}}$ и s. Кроме того, соотношение (7) показывает их разное качественное влияние на выполнение условия изотропии среды.

АНАЛИЗ ЗАВИСИМОСТИ СКОРОСТЕЙ АКУСТИЧЕСКИХ И РОТАЦИОННЫХ ВОЛН ОТ ПАРАМЕТРОВ МИКРОСТРУКТУРЫ

В отличии от классической теории упругости, рассматриваемая здесь трехмерная модель кристаллической среды учитывает ротационные степени свободы. Но наблюдать экспериментально в лабораторных условиях распространение ротационных волн в твердых телах до сих пор никому не удавалось [25]. Известно лишь, что их близкими аналогами являются спиновые волны в ферромагнетиках [26] и волны директора в жидких кристаллах [27]. В связи с этим вызывают интерес теоретические оценки скоростей таких волн. Анализ соотношений (5) с учетом положительных жесткостей пружин Ki ($i = 0{\kern 1pt} - {\kern 1pt} 4$) показывает, что из скоростей с1, с2, с3, с4 наибольшей является скорость продольных волн с1, а наименьшей – скорость ротационных волн с3.

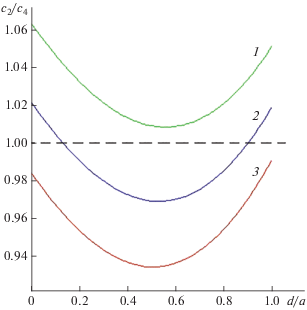
На рис. 4 приведены зависимости отношения скорости поперечных волн с2 к скорости ротационных волн с4 от относительного размера частиц d/a при K10 = 0.5, K30 = 1.2, K40 = 1.4 (здесь и далее Ki0 = Ki/K0). Из этого рисунка видно, что увеличение параметра моментных взаимодействий K20 приводит к тому, что с4 > с2. Кроме того, численный анализ показывает, что увеличение параметров K30 и K40, а также уменьшение параметра K10 ведет к противоположному результату – с2 > с4. Таким образом, в рассматриваемой среде скорости с2 и с4 одного порядка. При этом в кристалле фуллерита с простой кубической решеткой c1 = = 2943 м/c, c2 = 2325 м/c [28].

Рис. 4.

Зависимость отношения скоростей поперечных и ротационных волн с2/c4 от относительного размера частиц при K1/K0 = 0.5, K3/K0 = 1.2, K4/K0 = 1.4. Кривая 1 соответствует K2/K0 = 0.2, кривая 2 – K2/K0 = = 0.3, кривая 3 – K2/K0 = 0.4.

ЗАКЛЮЧЕНИЕ

В данной работе методом структурного моделирования построена трехмерная математическая модель простой кубической решетки кристалла фуллерита из сферических частиц, обладающих тремя трансляционными и тремя ротационными степенями свободы. Найдено условие на параметры микроструктуры такой среды, при выполнении которого среда становится изотропной. Получены аналитические зависимости скоростей акустических и ротационных волн от параметров микроструктуры. Наибольшей среди всех скоростей является скорость продольных волн с1, а наименьшей – скорость ротационных волн с3. Скорость ротационных волн с4 может превосходить скорость поперечных волн с2. Соотношению с4 > с2 способствуют увеличение параметров моментных взаимодействий K10 и K20, а также уменьшение параметров K30 и K40.

Работа выполнена в рамках государственного задания ИПФ РАН на проведение фундаментальных научных исследований на 2021–2023 гг. по теме № 0030-2021-0025, а также при финансовой поддержке Российского фонда фундаментальных исследований (проекты № 19-08-00965-а и 18-29-10073-мк).

Список литературы

  1. Гуляев Ю.В., Лагарьков А.Н., Никитов С.А. // Вестн. РАН. 2008. Т. 78. № 5. С. 438.

  2. Shining Zhu, Xiang Zhang // Nat. Sci. Rev. 2018. V. 5. No. 2. P. 131.

  3. Бобровницкий Ю.И. // Акуст. журн. 2014. Т. 60. № 4. С. 347; Bobrovnitskii Yu.I. // Acoust. Phys. 2014. V. 60. No. 4. P. 371.

  4. Бобровницкий Ю.И. // Акуст. журн. 2015. Т. 61. № 3. С. 283; Bobrovnitskii Yu.I. // Acoust. Phys. 2015. V. 61. No. 3. P. 255.

  5. Федотовский В.С. // Акуст. журн. 2018. Т. 64. № 5. С. 547; Fedotovskii V.S. // Acoust. Phys. 2018. V. 64. No. 5. P. 548.

  6. Cummer S.A., Christensen J., Alù A. // Nat. Rev. Mater. 2016. V. 1. Art. No. 16001.

  7. Zhou L., Jiang H. // Phys. Stat. Sol. B. 2016. V. 253. No. 7. P. 1331.

  8. Бобровницкий Ю.И., Томилина Т.М. // Акуст. журн. 2018. Т. 64. № 5. С. 517; Bobrovnitskii Yu.I., Tomilina T.M. // Acoust. Phys. 2018. V. 64. No. 5. P. 519.

  9. Сидоров Л.Н., Юровская М.А., Борщевский А.Я. и др. Фуллерены. Уч. пособ. М.: Экзамен, 2005. 688 с.

  10. Бланк В.Д., Левин В.М., Прохоров В.М. и др. // ЖЭТФ. 1998. Т. 114. С. 1364. Blank V.D., Levin V.M., Prokhorov V.M. et al. // J. Exp. Theor. Phys. 1998. V. 87. P. 741.

  11. Кобелев Н.П., Моравский А.П., Сойфер Я.М. и др. // ФТТ. 1994. Т. 36. № 9. С. 2732.

  12. Руденко О.В. // Изв. РАН. Сер. физ. 2015. Т. 79. № 10. С. 1369; Rudenko O.V. // Bull. Russ. Acad. Sci. Phys. 2015. V. 79. No. 10. P. 1215.

  13. Ерофеев В.И., Герасимов С.И., Кажаев В.В., Павлов И.С. // Изв. РАН. Сер. физ. 2016. Т. 80. № 10. С. 1333; Erofeev V.I., Gerasimov S.I., Kazhaev V.V., Pavlov I.S. // Bull. Russ. Acad. Sci. Phys. 2016. V. 80. No. 10. P. 1203.

  14. Ерофеев В.И., Леонтьева А.В., Мальханов А.О. // Изв. РАН. Сер. физ. 2018. Т. 82. № 5. С. 591; Erofeev V.I., Leonteva A.V., Malhanov A.O. // Bull. Russ. Acad. Sci. Phys. 2018. V. 82. No. 5. P. 520.

  15. Chunyu Li, Tsu-Wei Chou // Int. J. Sol. Struct. 2003. V. 40. No. 10. P. 2487.

  16. Павлов И.С., Потапов А.И. // ДАН. 2008. Т. 421. № 3. С. 348; Pavlov I.S., Potapov A.I. // Dokl. Phys. 2008. V. 53. No. 7. P. 408.

  17. Pavlov I.S., Potapov A.I., Maugin G.A. // Int. J. Sol. Struct. 2006. V. 43. No. 20. P. 6194.

  18. Ерофеев В.И., Павлов И.С. Структурное моделирование метаматериалов. Нижний Новгород: ИПФ РАН, 2019. 196 с.

  19. Vasiliev A.A., Pavlov I.S. // IOP Conf. Ser. Mater. Sci. Engin. 2018. V. 447. Art. No. 012079.

  20. Spadoni A., Ruzzene M. // J. Mech. Phys. Sol. 2012. V. 60. P. 156.

  21. Конек Д.А., Войцеховски К.В., Плескачевский Ю.М., Шилько С.В. // МКМК. 2004. Т. 10. № 1. С. 35.

  22. Vasiliev A.A., Miroshnichenko A.E., Dmitriev S.V. // Eur. J. Mech. A. 2014. V. 46. P. 96.

  23. Altenbach H., Maugin G.A., Erofeev V.I. Mechanics of generalized continua. Berlin, Heidelberg: Springer-Verlag, 2011. 350 p.

  24. Новацкий В. Теория упругости. М.: Мир, 1975. 872 с.

  25. Erofeev V.I., Pavlov I.S., Vikulin A.V. // Mater. Phys. Mech. 2018. V. 35. No. 1. P. 53.

  26. Ахиезер А.И., Барьяхтар В.Г., Пелетминский С.В. Спиновые волны. М.: Наука, 1967. 368 с.

  27. Lee J.D., Eringen A.C. // J. Chem. Phys. 1971. V. 54. No. 12. P. 5027.

  28. Yildirim T., Harris A.B. // Phys. Rev. B. 1992. V. 46. Art. No. 7878.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал