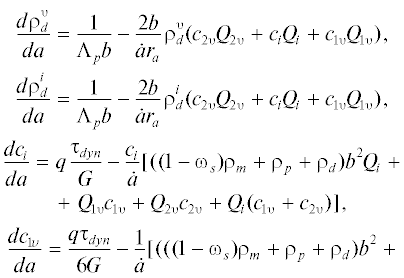Известия РАН. Серия физическая, 2021, T. 85, № 7, стр. 1002-1007

ВВЕДЕНИЕ

Экспериментальные исследования процессов деформационного упрочнения гетерофазных сплавов, как правило, ограничиваются рассмотрением влияния только лишь какого-то одного размера частиц в рамках одной объемной доли. Этот размер частиц определяется технологией приготовления таких сложных систем [1, 2]. Математическое моделирование, учитывающее реальные физические процессы, которые протекают во время пластической деформации, позволяет варьировать различные параметры, влияющие на поведение кривых течения, изменение плотности дислокаций. Кроме того, математическое моделирование обеспечивает прогноз протекания этих процессов и выявление управляющих параметров, отвечающих за деформационное поведение гетерофазных сплавов и их максимальную прочность.

В данной работе методом математического моделирования проведен расчет кривых течения, характеристик деформационной дефектной структуры и параметров зоны сдвига гетерофазного кристаллического материала с некогерентными дисперсными частицами и алюминиевой матрицей. Были исследованы материалы с разными объемными долями упрочняющей фазы. В рамках каждой из трех рассмотренных объемных долей варьировался размер частиц от нано- до микроразмеров.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Модель пластической деформации монокристаллов гетерофазных материалов с недеформируемой упрочняющей фазой [3], развиваемая в данной работе, сформулирована на основе детального анализа последовательных дислокационных превращений в дисперсно-упрочненных материалах, сопровождающихся формированием различных элементов дефектной структуры. Сдвигообразующая скользящая дислокационная петля, движущаяся от источника, многократно пересекается с порогообразующими дислокациями леса. В результате этого, помимо хорошо известных дислокационных структур, формирующихся в зоне сдвига при движении матричной (сдвигообразующей) дислокации, таких как кольца Орована, призматические петли [4–8], могут появляться протяженные диполи между частицами [3]. Такие диполи формируются в результате неполной аннигиляции ветвей дислокаций, огибающих недеформируемые частицы при их преодолении. Неполная аннигиляция ветвей дислокаций возможна лишь при достижении критической плотности дислокаций ${{\rho }_{c}}$ [3]. При этом порогообразующие дислокации выводят участки скользящей дислокации на достаточно большие расстояния вверх и вниз от плоскости ее первоначального скольжения, лишая при этом дислокации, огибающие частицы, возможности аннигилировать.

При переходе через критическую плотность дислокаций ${{\rho }_{c}}$ изменяется характер дислокационной структуры зоны сдвига. При плотностях дислокаций $\rho < {{\rho }_{c}}$ дислокации накапливаются на препятствиях дислокационной природы, ограничивающих зону сдвига, и на частицах (геометрически необходимые дислокации [9, 10]). Размер зоны сдвига при $\rho < {{\rho }_{c}}$ определяется междислокационными взаимодействиями. При плотности дислокаций больше критической $\rho > {{\rho }_{c}}$ появляются дополнительные элементы дислокационной структуры – дипольные и мультипольные дислокационные конфигурации, вытянутые от частицы к частице. Такие конфигурации могут быть достаточно прочными протяженными барьерами, чтобы обеспечить накопление на них большого числа дислокаций. Появление сильных внутризонных барьеров существенно изменяет характер дислокационной структуры зоны сдвига, величину свободного пробега дислокаций и, следовательно, интенсивность их накопления [3, 11, 12].

Таким образом, математическая модель включает уравнения баланса сдвигообразующих дислокаций, призматических дислокационных петель межузельного и вакансионного типа, дислокаций в дипольных конфигурациях вакансионного и межузельного типа, межузельных атомов, моновакансий и бивакансий, а также уравнение, связывающее скорость деформации с дефектностью материала и приложенным воздействием [11, 13, 14]:

(1)

Здесь а – деформация сдвига; $\dot {a}$ – скорость деформации, F – параметр, определяемый формой дислокационных петель и их распределением в зоне сдвига; D – диаметр зоны сдвига; b – модуль вектора Бюргерса; ω_s – доля винтовых дислокаций; ${{P}_{{as}}}$ – вероятность аннигиляции винтовых дислокаций; ${{r}_{a}}$ – критический радиус захвата, ${{\tau }_{{dyn}}}$ – напряжение, избыточное над статическим сопротивлением движению дислокаций; ${{Q}_{j}}$ – кинетический коэффициент; ν_D – частота Дебая; k – постоянная Больцмана; T – температура деформирования; 〈χ〉 – отношение средней длины дислокаций, накопившихся на частицах, к их размеру; Λ_p – расстояние между частицами второй фазы, δ – размер частиц; q – параметр, определяющий интенсивность генерации точечных дефектов; G – модуль сдвига; B – параметр, определяемый вероятностью образования дислокационных барьеров, ограничивающих зону сдвига; ρ – плотность дислокаций, ξ – множитель Смоллмэна, ${{\rho }_{p}} = \rho _{p}^{i} + \rho _{p}^{{{\upsilon }}}$ – плотность призматических дислокационных петель, ${{\rho }_{d}} = \rho _{d}^{i} + \rho _{d}^{{{\upsilon }}}$ – плотность дислокаций в дипольных конфигурациях; $\tau $ – сдвиговое напряжение; Λ – длина свободного дислокационного сегмента; ${{\beta }_{r}}$ – доля реагирующих дислокаций леса.

Атермическая составляющая сопротивления движению дислокаций τ_а в дисперсно-упрочненном сплаве с некогерентными частицами обусловлена напряжением трения τ_f, взаимодействием с реагирующими дислокациями леса τ_d и напряжением обхода частиц (напряжением Орована) τ_Or: τ_а = τ_f + τ_d + τ_Or.

Для решения системы обыкновенных дифференциальных уравнений, описывающих баланс деформационных линейных и точечных дефектов, необходимо задать начальные значения концентраций точечных дефектов и плотностей дислокаций. Начальная концентрация точечных дефектов соответствует концентрации термодинамически равновесных точечных дефектов при данной температуре, начальная плотность сдвигообразующих дислокаций соответствует состоянию недеформированного кристалла, предполагается отсутствие дислокационных призматических петель и дислокаций в дипольных конфигурациях при $a = 0{\text{:}}$ $\rho _{m}^{{(0)}} = {{10}^{{12}}}$ м^–2, $\rho _{p}^{{(0)}} = \rho _{d}^{{(0)}} = 0,$ $c_{i}^{{(0)}} = \exp \left( {{{ - U_{i}^{f}} \mathord{\left/ {\vphantom {{ - U_{i}^{f}} {kT}}} \right. \kern-0em} {kT}}} \right),$ $c_{{{\upsilon }}}^{{(0)}} = \exp \left( {{{ - U_{{{\upsilon }}}^{f}} \mathord{\left/ {\vphantom {{ - U_{{{\upsilon }}}^{f}} {kT}}} \right. \kern-0em} {kT}}} \right),$ $c_{{2{{\upsilon }}}}^{{(0)}} = \exp \left( {{{ - U_{{2{{\upsilon }}}}^{f}} \mathord{\left/ {\vphantom {{ - U_{{2{{\upsilon }}}}^{f}} {kT}}} \right. \kern-0em} {kT}}} \right).$

Основные расчеты проведены при следующих значениях параметров для монокристаллов дисперсно-упрочненных сплавов с алюминиевой матрицей: b = 2.5 ⋅ 10^–10 м, F = 4, ν_D = 10¹³ c^–1, β_r = 0.14, ξ = 0,5, τ_f =1 МПа, α_dyn ≈ 0.33, k = $1.38 \cdot {{10}^{{ - 23}}}$ Дж/К, ω_s = 0.3, $U_{{{\upsilon }}}^{f} = 0.73$ эВ, $U_{{2{{\upsilon }}}}^{f} = 1.37$ эВ, $U_{i}^{f} = 3.2$ эВ. Объемная доля упрочняющей фазы задавалась равной f₁ = 10^–4%, f₂ = 0.01%, f₃ = 0.1% для материалов с разными масштабными характеристиками упрочняющей фазы. Размеры упрочняющих частиц и расстояния между ними варьировались в физически реализуемых пределах.

Решение уравнений баланса элементов деформационной дефектной среды осуществлялось методом Рунге–Кутты–Мерсона четвертого порядка точности [15] с автоматическим выбором шага интегрирования, позволяющим решать умеренно и сильно жесткие системы обыкновенных дифференциальных уравнений. Автоматический выбор шага позволяет значительно сократить время вычислений.

АНАЛИЗ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ

Решение системы (1) позволяет получить зависимости плотностей всех линейных и точечных дефектов от степени деформации, а также кривые течения $\tau (a).$ Модель позволяет анализировать влияние температуры деформации, размера упрочняющих частиц и расстояния между ними на механические характеристики материала.

Предел текучести дисперсно-упрочненных материалов с фиксированной объемной долей упрочняющей фазы зависит от дисперсности второй фазы: чем меньше размер упрочняющих частиц (при этом и расстояние между частицами меньше), тем выше предел текучести (рис. 1). Это утверждение справедливо для материалов с разными объемными долями упрочняющих частиц (рис. 1а–1в). Это объясняется тем, что в материалах с наноразмерными частицами и малым расстоянием между ними напряжение Орована больше, чем в материалах с меньшей степенью дисперсности. Именно напряжение Орована дает значимый вклад в предел текучести.

Рис. 1.

Кривые деформационного упрочнения сплава на основе алюминия с некогерентными недеформируемыми частицами, объемная доля которых равна: а – 10^–4, б – 0.01, в – 0.1%. Размер упрочняющих частиц: 10 (1), 20 (2), 50 (3), 100 (4), 200 (5), 500 (6) нм.

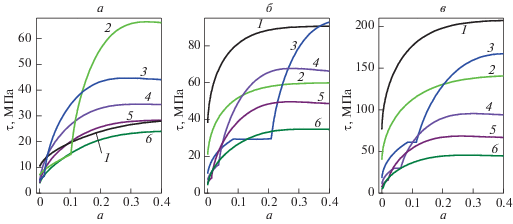
Рисунок 1 демонстрирует различие в форме кривых течения для материалов с разными масштабными характеристиками упрочняющей фазы. Видно, что в материале с размером частиц $\delta $ = = 10 нм и самой малой из исследуемых объемной доли упрочняющей фазы могут формироваться очень низкие напряжения (рис. 1а, кривая 1). Для такого сплава упрочняющий эффект обеспечивают призматические петли, плотность которых достаточно низкая. В этом материале дипольные структуры не формируются, так как не достигается критическая плотность дислокаций. При увеличении размера частиц в 2 раза ($\delta $ = 20 нм) уже при степени деформации а = 0.1 начинают формироваться дислокационные дипольные конфигурации (рис. 1а, кривая 2), которые вносят существенный вклад в упрочнение материала. Для материалов с более крупными упрочняющими частицами $\delta $ = 50–500 нм выполняется следующая зависимость: чем крупнее частицы в пределах одной объемной доли упрочняющей фазы, тем меньшее напряжение течения достигается в ходе процесса пластической деформации (рис. 1а–1в).

В материале с размером частиц $\delta $ = 20 нм при появлении дислокационных диполей увеличивается плотность сдвигообразующих дислокаций ${{\rho }_{m}}$ (рис. 2а, кривая 1). Возрастание ${{\rho }_{m}}(\delta )$ происходит в интервале наноразмерных частиц, а в зоне микроразмерных частиц ${{\rho }_{m}}(\delta )$ уменьшается с увеличением размера частиц в материале. Максимальное значение как плотности сдвигообразующих дислокаций ${{\rho }_{m}},$ так и плотности дислокаций в дипольных конфигурациях ${{\rho }_{d}}$ достигается в материале с размером упрочняющих частиц $\delta $ = 50 нм (рис. 2а, кривые 1, 3). В материалах с микроразмерными частицами основной и сопоставимый вклад в упрочнение вносят сдвигообразующие и дипольные дислокации, причем плотность ${{\rho }_{m}}$ немного превышает ${{\rho }_{d}}.$

Рис. 2.

Зависимость плотности сдвигообразующих дислокаций (1), призматических петель (2) и дислокаций в дипольных конфигурациях (3) от размера упрочняющих частиц. Степень деформации – 0.2. Объемная доля упрочняющей фазы: а – 10^–4, б – 0.01%.

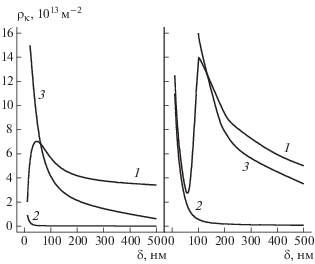
Увеличение объемной доли некогерентных дисперсных частиц приводит к заметному увеличению прочностных свойств (напряжения течения, предела текучести и деформационного упрочнения) в материале либо с самыми мелкими из рассматриваемых частиц $\delta $ = 10 нм (рис. 1а–1в, кривая 1), либо с более крупными частицами $\delta $ = = 100–500 нм (рис. 1а–1в, кривые 4–6). Для материалов с размером упрочняющих частиц $\delta $ = 20–50 нм уже нет такой однозначной зависимости (рис. 1, кривые 2, 3). Для данных материалов процесс пластической деформации может проходить по разному сценарию в зависимости от объемной доли упрочняющей фазы. Пластическая деформация протекает либо только в докритической области плотностей дислокаций, тогда в зоне сдвига генерируются сдвигообразующие дислокации и призматические петли, либо сначала в докритической области, а при достижении в материале критической плотности дислокаций начинают формироваться дислокационные диполи.

При появлении диполей их плотность существенно возрастает и вносит большой вклад в упрочнение материала. В этом случае может сложиться ситуация, когда в материале с меньшей объемной долей упрочняющей фазы напряжение течения будет больше, чем в материале большей объемной долей упрочняющей фазы (рис. 1а, 1б, кривая 2 со степени деформации 0.2, кривая 3 до деформации 0.23). На рис. 2 видно, что в материале с $\delta $ = 50 нм дислокационные диполи уже присутствуют при деформации 0.2 в материале с объемной долей f₁ = 10^–4% (рис. 2а, кривая 3), но не начали формироваться в материале с большей объемной долей f₂ = 0.01% (рис. 2б, кривая 3). Это объясняет большую плотность дислокаций и большее напряжение течения в материале с меньшей объемной долей упрочняющей фазы до степени деформации 0.2. В материале с размером частиц $\delta $ = 20 нм и объемной долей f₁ = 10^–4% была достигнута критическая плотность дислокаций при деформации а = 0.1, после чего появились дислокационные диполи (рис. 2а, кривая 3), и их плотность начала резко расти, в отличие от материала с таким же размером частиц, но объемной долей f₂ = 0.01%, где критическая плотность не была достигнута, и диполи не появились (рис. 2б, кривая 3).

Заметим, что рис. 2 иллюстрирует процесс перехода дислокационных диполей в разряд сдвигообразующих дислокаций: при наличии в материале дипольных конфигураций плотность сдвигообразующих дислокаций заметно выше (рис. 2а, 2б, кривые 1, 3).

Теоретический расчет размера зоны сдвига D в зависимости от величины сдвига не выявляет резких отклонений в размере зоны сдвига (рис. 3) исследованных дисперсно-упрочненных сплавов. На рис. 3а–3в продемонстрировано изменение размера зоны сдвига от степени пластической деформации для сплавов с разными объемными долями упрочняющих некогерентных частиц. Видно, что размер зоны сдвига в основном уменьшается с ростом величины деформации в пределах 30 ≤ D ≤ 350 мкм при всех исследованных значениях объемных долей и размеров упрочняющих частиц. При этом кривые течения существенно отличаются при вариации масштабных характеристик упрочняющей фазы. Механические свойства материала определяются в основном размером частиц, типом дислокаций, формирующихся вблизи частиц в зоне сдвига, и способностью трансформации дипольных дислокационных структур в сдвигообразующие дислокации.

Рис. 3.

Зависимость диаметра зоны сдвига от величины деформации в сплаве с упрочняющими частицами размером, нм: 10 (а); 20 (б); 50 (в). Объемная доля частиц: 10^–4 (1), 0.01 (2), 0.1 (3) %.

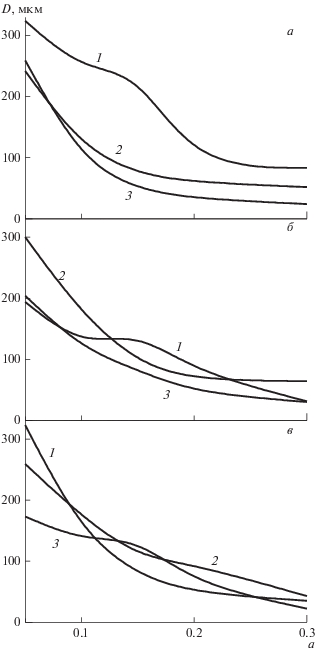
Изменение максимальных прочностных свойств на кривой течения при разных значениях объемной доли и в зависимости от размера упрочняющих частиц показано на рис. 4. Видно, что при увеличении размера частиц в пределах одной объемной доли упрочняющей фазы наблюдается уменьшение максимальной прочности ${{\tau }_{{max}}}.$ Но в области наноразмерных частиц ($\delta $ = 10–100 нм) такая монотонная зависимость нарушается (рис. 4, кривые 1, 2, 3). Кроме того, при большей объемной доле наноразмерных частиц упрочняющей фазы ($\delta $ = 20–50 нм) теоретический расчет прогнозирует меньшую максимальную прочность ${{\tau }_{{max}}}$ (рис. 4, кривые 1, 2). Это обусловлено составом дислокационного ансамбля материалов с разной степенью дисперсности. При меньшей объемной доле частиц в процессе деформации начинают формироваться дипольные структуры (рис. 2а). Причем, чем позже в процессе пластической деформации начинается образование диполей, тем быстрее и значительнее растет их плотность, что вносит вклад в общую плотность дислокаций и, как следствие, в упрочнение материала (рис. 2а, 2б). В материале с большей объемной долей упрочняющей фазы критическая плотность дислокаций в процессе деформации не достигается, и диполи не формируются (рис. 2б). Поэтому плотность дислокаций в процессе деформации растет незначительно, оставаясь меньше, чем в материале с тем же размером частиц, но с меньшей объемной долей упрочняющей фазы.

Рис. 4.

Зависимость наибольшего значения напряжения течения от размера частиц в сплавах с объемными долями упрочняющей фазы: 10^–4 (1), 0.01 (2), 0.1 (3) %.

ЗАКЛЮЧЕНИЕ

В ходе исследования выполнены математическое моделирование и теоретический расчет кривых течения дисперсно-упрочненных кристаллических сплавов с алюминиевой матрицей для трех объемных долей некогерентных дисперсных частиц при комнатной температуре с учетом вариации размеров частиц для каждой объемной доли в диапазоне от нано- до микроразмеров.

При малой объемной доле наноразмерных частиц максимальным прочностным свойствам кривых течения соответствует наличие в дислокационном ансамбле не только сдвигообразующих дислокаций и дислокационных призматических петель, но и дислокаций в дипольных конфигурациях. Диполи начинают формироваться только при достижении в материале критической плотности дислокаций в процессе пластической деформации. Чем больше степень деформации, при которой образовались дипольные конфигурации, тем быстрее их плотность возрастает в процессе пластической деформации. Появление дипольных дислокационных конфигураций создает условия для значительного увеличения напряжения течения.

В сплаве с микроразмерными частицами с самого начала пластической деформации в дислокационном ансамбле присутствуют сдвигообразующие дислокации, призматические петли и дипольные конфигурации. В этих материалах плотность дислокаций в процессе пластической деформации растет монотонно, как и напряжение течения. В материалах с микроразмерными частицами прочностные свойства существенно ниже, чем в материалах с наноразмерными частицами при одной и той же объемной доле упрочняющей фазы.

Максимальные величины напряжения течения в материалах с микроразмерными упрочняющими частицами возрастают при увеличении объемной доли частиц. В материалах с наноразмерными частицами при малых величинах объемной доли частиц возможны ситуации, когда в материалах с меньшей объемной долей упрочняющей фазы максимальная прочность больше, чем в материалах с большей объемной долей частиц. На наш взгляд, этот факт надо учитывать при изготовлении таких материалов. Математическая модель позволяет прогнозировать усиление прочностных свойств гетерофазных кристаллических материалов, упрочненных дисперсными некогерентными частицами от нано- до микроразмеров.

Работа выполнена в рамках государственного задания Министерства науки и высшего образования Российской Федерации (тема № FEMN-2020-0004).