1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 86, № 11, 2022

Известия РАН. Серия физическая, 2022, T. 86, № 11, стр. 1634-1640

Об аналитическом описании динамики планарных импульсов, распространяющихся в режиме туннельной ионизации

В. А. Халяпин 1, 2, *, А. Н. Бугай 3

1 Федеральное государственное автономное образовательное учреждение высшего образования “Балтийский федеральный университет имени И. Канта”
Калининград, Россия

2 Федеральное государственное образовательное бюджетное учреждение высшего образования “Калининградский государственный технический университет”
Калининград, Россия

3 Международная межправительственная организация “Объединенный институт ядерных исследований”
Дубна, Россия

* E-mail: slavasxi@gmail.com

Поступила в редакцию 30.06.2022
После доработки 15.07.2022
Принята к публикации 22.07.2022

Полный текст (PDF)

Аннотация

На основе метода моментов рассмотрена задача о динамике планарного импульса, распространяющегося в режиме туннельной ионизации. Получена система уравнений на параметры сигнала, с помощью метода Ляпунова найдены условия его квазиустойчивого распространения.

ВВЕДЕНИЕ

Исследование динамики интенсивных импульсов, распространяющихся в режиме ионизации, представляет как теоретический, так и практический интерес в связи с их применением в различных областях: дистанционном зондировании атмосферы [1], управлении молниями [2], генерации суперконтинуума [3], генерации терагерцового излучения [4] и др. Хорошо известно, что решение нелинейного уравнения Шрёдингера (НУШ) устойчиво только для одномерного случая $D = 1$, который отвечает чисто пространственным или временным сигналам. При размерности $D = 2,$ что соответствует пучкам или планарным пространственно-временным импульсам и при $D = 3,$ соответствующей оптическим пулям, решения не устойчивы [5]. Для стабилизации сигналов с $D > 1$ были предложены такие механизмы как насыщающая нелинейность [6], конкурирующие нелинейности [7], дифракция или дисперсия более высокого порядка [8], градиентный волновод [9], генерация второй гармоники [10]. Было показано, что ионизация также может стабилизировать сигнал [11–18]. Эта стабилизация обусловлена балансом между самофокусировкой, дифракцией и плазменной расходимостью. Известно, что ионизация приводит к сдвигу спектра импульса в сторону более высоких частот [19–21]. Это обусловлено генерацией свободных электронов и приводит к отрицательному значению показателя преломления и, следовательно, к синему смещению спектра сигнала. Это явление противоположно хорошо известному вынужденному комбинационному саморассеянию (ВКС) [22–26].

Ионизация диэлектрика интенсивным световым импульсом может быть описана с помощью формулы Келдыша [27]. Различают два предельных режима (в зависимости от параметра Келдыша): многофотонный и режим туннельной ионизации. Аналитическое исследование импульсов, распространяющихся в режиме туннельной ионизации, представляет интерес поскольку область аномальной дисперсии групповой скорости для большинства сред относится к инфракрасной полосе пропускания [28]. Предел туннельной ионизации изучался в основном с помощью экспериментов и численного моделирования [28]. Это связано с математическими затруднениями, которые возникают при описании вклада туннельной ионизации в динамику сигнала. В работе [19] формула Келдыша для режима туннельной ионизации была аппроксимирована линейной функцией, а авторы [29] предложили использовать для этой цели степенную зависимость скорости ионизации от интенсивности. Недостатками этих подходов является то, что параметры приближенных формул для скорости ионизации приходится каждый раз подбирать в зависимости от рассматриваемого диапазона интенсивностей. В настоящей работе мы предлагаем подход к приближенному учету вклада туннельной ионизации, лишенный вышеотмеченных недостатков.

МЕТОД МОМЕНТОВ

В настоящей работе рассматривается динамика планарных сигналов, распространяющихся в режиме туннельной ионизации, с помощью метода моментов [25, 30, 31]. Уравнения, описывающие соответствующую динамику, имеют вид

(1)
$\begin{gathered} \frac{{\partial \psi }}{{\partial z}} + \frac{{i{{\beta }_{2}}}}{2}\frac{{{{\partial }^{2}}\psi }}{{\partial {{\tau }^{2}}}} - \frac{{{{\beta }_{3}}}}{6}\frac{{{{\partial }^{3}}\psi }}{{\partial {{\tau }^{3}}}} - i\gamma \psi {{\left| \psi \right|}^{2}} + \frac{\gamma }{\omega }\frac{\partial }{{\partial \tau }}\left( {\psi {{{\left| \psi \right|}}^{2}}} \right) + \\ + \,\,i\gamma {{T}_{R}}\psi \frac{{\partial {{{\left| \psi \right|}}^{2}}}}{{\partial \tau }} + i\eta \psi \int\limits_{ - \infty }^\tau W d\tau {\kern 1pt} ' - \frac{{i\mu }}{2}\frac{{{{\partial }^{2}}\psi }}{{\partial {{x}^{2}}}} = 0. \\ \end{gathered} $
Здесь $\omega $ – центральная частота сигнала, $k$ – волновое число на центральной частоте, $z$ – координата, вдоль которой распространяется сигнал, $x$ – поперечная координата, $\tau = t - {z \mathord{\left/ {\vphantom {z {{{\vartheta }_{g}}}}} \right. \kern-0em} {{{\vartheta }_{g}}}}$ – время в сопутствующей системе координат, ${{\vartheta }_{g}}$ – групповая скорость на частоте $\omega ,$ $\mu = {1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0em} k},$ $\eta = {{s\omega {{\tau }_{c}}{{N}_{0}}} \mathord{\left/ {\vphantom {{s\omega {{\tau }_{c}}{{N}_{0}}} 2}} \right. \kern-0em} 2}$ – параметр, связанный с электронной плазмой, $s = {{{{k}_{0}}\omega {{\tau }_{с}}} \mathord{\left/ {\vphantom {{{{k}_{0}}\omega {{\tau }_{с}}} {{{n}_{0}}{{N}_{c}}\left( {1 + {{\omega }^{2}}\tau _{c}^{2}} \right)}}} \right. \kern-0em} {{{n}_{0}}{{N}_{c}}\left( {1 + {{\omega }^{2}}\tau _{c}^{2}} \right)}}$ – поперечное сечение лавинной ионизации, ${{N}_{c}} = {{{{\varepsilon }_{0}}{{m}_{e}}{{\omega }^{2}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{0}}{{m}_{e}}{{\omega }^{2}}} {{{e}^{2}}}}} \right. \kern-0em} {{{e}^{2}}}}$ – критическая плотность плазмы, выше которой плазма перестает быть прозрачной, ${{\varepsilon }_{0}}$ – восприимчивость вакуума, ${{\tau }_{c}}$ – время столкновения электронов, $e$ и $m$ – соответственно заряд и масса электрона, ${{N}_{0}}$ – концентрация неионизированных молекул, $W$ – степень ионизации, определяемая формулой Келдыша в пределе малых значений параметра Келдыша (режим туннельной ионизации). ${{\beta }_{2}}$ – коэффициент дисперсии групповой скорости (ДГС), ${{\beta }_{3}}$ – положительный параметр, определяющий дисперсию третьего порядка, $\gamma $ – коэффициент кубической нелинейности, ${{T}_{R}}$ – характеризует вклад ВКС. Коэффициент ${{\beta }_{2}}$ положителен, если центральная частота импульса лежит в области нормальной дисперсии групповой скорости, и отрицателен в противоположном случае. Зависимость степени ионизации $W$ от интенсивности I для диэлектрика в пределе туннельной ионизации определяется формулой Келдыша [27].
(2)
$W = {{W}_{0}}{{\left( {\frac{{\left| \psi \right|}}{{{{B}_{T}}}}} \right)}^{{5{\text{/}}2}}}\exp \left( { - \frac{{{{B}_{T}}}}{{\left| \psi \right|}}} \right).$
Здесь ${{W}_{0}}\, = \,{{\sqrt \pi U_{i}^{{5{\text{/}}2}}{{m}^{{3{\text{/}}2}}}} \mathord{\left/ {\vphantom {{\sqrt \pi U_{i}^{{5{\text{/}}2}}{{m}^{{3{\text{/}}2}}}} {9\sqrt 8 {{\hbar }^{4}}{{N}_{0}}}}} \right. \kern-0em} {9\sqrt 8 {{\hbar }^{4}}{{N}_{0}}}},$ ${{B}_{T}}\, = \,{{\pi {{m}^{{1{\text{/}}2}}}U_{i}^{{3{\text{/}}2}}} \mathord{\left/ {\vphantom {{\pi {{m}^{{1{\text{/}}2}}}U_{i}^{{3{\text{/}}2}}} {2e\hbar }}} \right. \kern-0em} {2e\hbar }},$ $\hbar $ – постоянная Планка, ${{U}_{i}}$ – потенциал ионизации.

Анализ динамики параметров импульса проводился на основе метода моментов. Пробное решение выберем в виде

(3)
$\psi = B\exp \left[ { - \frac{1}{2}{{{\left( {\frac{\tau }{{{{\tau }_{p}}}}} \right)}}^{2}} - \frac{1}{2}{{{\left( {\frac{x}{a}} \right)}}^{2}} + i\left( {\phi - \frac{{C{{\tau }^{2}}}}{{2\tau _{p}^{2}}} - \frac{{\varepsilon {{x}^{2}}}}{{2{{a}^{2}}}}} \right)} \right],$
где $B$ – амплитуда сигнала, ${{\tau }_{p}}$ – его длительность, $C$ – параметр, определяющий частотную модуляцию, $\phi $ – фаза, $a$ – параметр, пропорциональный ширине планарного сигнала, $\varepsilon $ – описывает кривизну волновых поверхностей. Все параметры зависят от координаты $z.$ Определим моменты импульса в виде

(4)
$E = \int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {{{{\left| \psi \right|}}^{2}}d\tau dx} } ,$
(5)
$\tau _{p}^{2} = \frac{2}{E}\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {{{\tau }^{2}}{{{\left| \psi \right|}}^{2}}d\tau } dx} ,$
(6)
${{a}^{2}} = \frac{2}{E}\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {{{x}^{2}}{{{\left| \psi \right|}}^{2}}d\tau } dx} ,$
(7)
$C = \frac{i}{E}\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {\tau \left( {\psi {\text{*}}\frac{{\partial \psi }}{{\partial \tau }} - \psi \frac{{\partial \psi {\text{*}}}}{{\partial \tau }}} \right){{{\left| \psi \right|}}^{2}}d\tau } dx} ,$
(8)
$\varepsilon = \frac{i}{E}\int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {x\left( {\psi {\text{*}}\frac{{\partial \psi }}{{\partial x}} - \psi \frac{{\partial \psi {\text{*}}}}{{\partial x}}} \right){{{\left| \psi \right|}}^{2}}d\tau } dx} .$

Следуя методу моментов, получаем систему уравнений

(9)
$E = {{B}^{2}}\pi {{\tau }_{p}}a = {\text{const}},$
(10)
$\frac{{d\nu }}{{dz}} = - \frac{C}{{{{L}_{d}}\nu }},$
(11)
$\frac{{d\rho }}{{dz}} = - \frac{\varepsilon }{{{{L}_{D}}\rho }},$
(12)
$\frac{{dC}}{{dz}} = - \frac{{\left( {1 + {{C}^{2}}} \right)}}{{{{L}_{d}}{{\nu }^{2}}}} + \frac{1}{{{{L}_{N}}\nu \rho }},$
(13)
$\frac{{d\varepsilon }}{{dz}} = - \frac{1}{{{{L}_{D}}{{\rho }^{2}}}}\left( {1 + {{\varepsilon }^{2}}} \right) + \frac{1}{{{{L}_{N}}\nu \rho }} - \frac{{\exp \left( { - \sqrt {{{{{I}_{T}}\nu \rho } \mathord{\left/ {\vphantom {{{{I}_{T}}\nu \rho } {{{I}_{0}}}}} \right. \kern-0em} {{{I}_{0}}}}} } \right)}}{{{{L}_{\eta }}{{\nu }^{{3{\text{/}}4}}}{{\rho }^{{7{\text{/}}4}}}}}.$
В системе (10)–(13) были введены безразмерные параметры $\nu = {{{{\tau }_{p}}} \mathord{\left/ {\vphantom {{{{\tau }_{p}}} {{{\tau }_{0}}}}} \right. \kern-0em} {{{\tau }_{0}}}},$ $\rho = {a \mathord{\left/ {\vphantom {a {{{a}_{0}}}}} \right. \kern-0em} {{{a}_{0}}}},$ где ${{\tau }_{0}},$ ${{a}_{0}}$ – начальные значения соответствующих параметров. Характерные дисперсионная, дифракционная, нелинейная и ионизационные длины определяются следующими выражениями ${{L}_{d}} = {{\tau _{0}^{2}} \mathord{\left/ {\vphantom {{\tau _{0}^{2}} {\left| {{{\beta }_{2}}} \right|}}} \right. \kern-0em} {\left| {{{\beta }_{2}}} \right|}},$ ${{L}_{D}} = {{a_{0}^{2}} \mathord{\left/ {\vphantom {{a_{0}^{2}} \mu }} \right. \kern-0em} \mu },$ ${{L}_{N}} = {{c{{n}_{0}}} \mathord{\left/ {\vphantom {{c{{n}_{0}}} {4\pi \gamma {{I}_{0}}}}} \right. \kern-0em} {4\pi \gamma {{I}_{0}}}},$ ${{L}_{\eta }} = {{I_{T}^{{7{\text{/}}4}}} \mathord{\left/ {\vphantom {{I_{T}^{{7{\text{/}}4}}} {2\sqrt \pi \eta {{W}_{0}}{{\tau }_{0}}I_{0}^{{7{\text{/}}4}}}}} \right. \kern-0em} {2\sqrt \pi \eta {{W}_{0}}{{\tau }_{0}}I_{0}^{{7{\text{/}}4}}}},$ где введены обозначения ${{I}_{{0,T}}} = {{c{{n}_{0}}B_{{0,T}}^{2}} \mathord{\left/ {\vphantom {{c{{n}_{0}}B_{{0,T}}^{2}} {8\pi }}} \right. \kern-0em} {8\pi }}.$ В выражении (13) для учета ионизационного слагаемого мы использовали оценку ${{{{I}_{T}}} \mathord{\left/ {\vphantom {{{{I}_{T}}} I}} \right. \kern-0em} I}\sim {{\left( {{{{{U}_{i}}} \mathord{\left/ {\vphantom {{{{U}_{i}}} {\hbar w}}} \right. \kern-0em} {\hbar w}}} \right)}^{2}} \gg 1$ и ключевое приближение $\exp \left( {{{{{B}_{T}}} \mathord{\left/ {\vphantom {{{{B}_{T}}} {\left| \psi \right|}}} \right. \kern-0em} {\left| \psi \right|}}} \right)\, \approx $ $ \approx \,\exp \left( {{{{{B}_{T}}} \mathord{\left/ {\vphantom {{{{B}_{T}}} {{{B}_{0}}}}} \right. \kern-0em} {{{B}_{0}}}}\, - \,\left( {{{{{B}_{T}}} \mathord{\left/ {\vphantom {{{{B}_{T}}} {2{{B}_{0}}}}} \right. \kern-0em} {2{{B}_{0}}}}} \right)\left( {{{{{r}^{2}}} \mathord{\left/ {\vphantom {{{{r}^{2}}} {{{R}^{2}}}}} \right. \kern-0em} {{{R}^{2}}}}\, + \,{{{{\tau }^{2}}} \mathord{\left/ {\vphantom {{{{\tau }^{2}}} {\tau _{p}^{2}}}} \right. \kern-0em} {\tau _{p}^{2}}}} \right)} \right),$ которое позволило нам учесть вклад туннельной ионизации в динамику сигнала.

СТАЦИОНАРНОЕ РЕШЕНИЕ И ЕГО УСТОЙЧИВОСТЬ

Для того чтобы найти параметры стационарного состояния и условия его устойчивости, перепишем (10)–(13) в виде

(14)
$\frac{{d\nu }}{{d\xi }} = \frac{{{{P}_{\nu }}}}{{{{m}_{\nu }}}},$
(15)
$\frac{{d{{P}_{\nu }}}}{{d\xi }} = - \frac{{\partial U}}{{\partial \nu }},$
(16)
$\frac{{d\rho }}{{d\xi }} = \frac{{{{P}_{\rho }}}}{{{{m}_{\rho }}}},$
(17)
$\frac{{d{{P}_{\rho }}}}{{d\xi }} = - \frac{{\partial U}}{{\partial \rho }} + \tilde {F}.$
Здесь ${{P}_{\nu }} = {{{{m}_{\nu }}\partial \nu } \mathord{\left/ {\vphantom {{{{m}_{\nu }}\partial \nu } {\partial \xi }}} \right. \kern-0em} {\partial \xi }} = {{ - C} \mathord{\left/ {\vphantom {{ - C} \nu }} \right. \kern-0em} \nu },$ ${{P}_{\rho }} = {{{{m}_{\rho }}\partial \rho } \mathord{\left/ {\vphantom {{{{m}_{\rho }}\partial \rho } {\partial \xi }}} \right. \kern-0em} {\partial \xi }} = {{ - \varepsilon } \mathord{\left/ {\vphantom {{ - \varepsilon } \rho }} \right. \kern-0em} \rho },$ ${{m}_{\nu }} = 1,$ ${{m}_{\rho }} = {{{{L}_{D}}} \mathord{\left/ {\vphantom {{{{L}_{D}}} {{{L}_{d}}}}} \right. \kern-0em} {{{L}_{d}}}},$ $\xi = {z \mathord{\left/ {\vphantom {z {{{L}_{d}}}}} \right. \kern-0em} {{{L}_{d}}}}.$ Систему (14)–(17) можно трактовать как механическую аналогию, описывающую движение частицы по поверхности с координатными осями $\nu $ и $\rho $ в потенциальном поле

(18)
$U = \frac{1}{{2{{\nu }^{2}}}} + \frac{{{{L}_{d}}}}{{2{{L}_{D}}{{\rho }^{2}}}} - \frac{{{{L}_{d}}}}{{{{L}_{N}}\nu \rho }}.$

При этом масса частицы зависит от направления движения. Роль внешней силы, действующей вдоль координаты $\rho ,$ играет ионизационное слагаемое $\tilde {F} = {{{{L}_{d}}\exp ( - \sqrt {{{{{I}_{T}}\nu \rho } \mathord{\left/ {\vphantom {{{{I}_{T}}\nu \rho } {{{I}_{0}}}}} \right. \kern-0em} {{{I}_{0}}}}} )} \mathord{\left/ {\vphantom {{{{L}_{d}}\exp ( - \sqrt {{{{{I}_{T}}\nu \rho } \mathord{\left/ {\vphantom {{{{I}_{T}}\nu \rho } {{{I}_{0}}}}} \right. \kern-0em} {{{I}_{0}}}}} )} {{{L}_{\eta }}{{\nu }^{{3{\text{/}}4}}}{{\rho }^{{11{\text{/}}4}}}}}} \right. \kern-0em} {{{L}_{\eta }}{{\nu }^{{3{\text{/}}4}}}{{\rho }^{{11{\text{/}}4}}}}}.$ Стационарное решение этой системы уравнений можно записать как

(19)
${{L}_{d}} = {{L}_{N}},$
(20)
$\frac{1}{{{{L}_{D}}}} = \frac{1}{{{{L}_{N}}}} - \frac{{\exp \left( { - \sqrt {{{{{I}_{T}}} \mathord{\left/ {\vphantom {{{{I}_{T}}} {{{I}_{0}}}}} \right. \kern-0em} {{{I}_{0}}}}} } \right)}}{{{{L}_{\eta }}}}.$

Выражения (19), (20) можно переписать в виде

(21)
${{\tau }_{0}} = \sqrt {\frac{{2\left| {{{\beta }_{2}}} \right|}}{{{{k}_{0}}{{n}_{2}}{{I}_{0}}}}} ,$
(22)
$\frac{1}{{{{a}_{0}}}} = \sqrt {{{k}_{0}}{{n}_{0}}\left( {\frac{{{{k}_{0}}{{n}_{2}}{{I}_{T}}}}{{2X}} - 2\sqrt \pi \eta {{W}_{0}}\sqrt {\frac{{2\left| {{{\beta }_{2}}} \right|}}{{{{k}_{0}}{{n}_{2}}{{I}_{T}}}}} \frac{{\exp ( - \sqrt X )}}{{{{X}^{{5{\text{/}}4}}}}}} \right)} .$
Здесь $X = {{{{I}_{T}}} \mathord{\left/ {\vphantom {{{{I}_{T}}} {{{I}_{0}}}}} \right. \kern-0em} {{{I}_{0}}}}$ и мы использовали соотношение ${{8\pi \gamma } \mathord{\left/ {\vphantom {{8\pi \gamma } {c{{n}_{0}}}}} \right. \kern-0em} {c{{n}_{0}}}} \equiv {{k}_{0}}{{n}_{2}},$ где ${{n}_{2}}$ – нелинейный показатель преломления среды. Из (21), (22) следует, что с ростом интенсивности длительность сигнала уменьшается, а ширина увеличивается. Подкоренное выражение в (25) должно быть положительным (равенство нулю подкоренного выражения соответствует бесконечной ширине сигнала). Из этого условия находим
(23)
${{I}_{0}} < {{4{{I}_{T}}} \mathord{\left/ {\vphantom {{4{{I}_{T}}} {{{{\left( {\tilde {W}\left( {2{{A}^{2}}} \right)} \right)}}^{2}}}}} \right. \kern-0em} {{{{\left( {\tilde {W}\left( {2{{A}^{2}}} \right)} \right)}}^{2}}}},$
где $A = {{4\eta {{W}_{0}}\sqrt {2\pi \left| {{{\beta }_{2}}} \right|} } \mathord{\left/ {\vphantom {{4\eta {{W}_{0}}\sqrt {2\pi \left| {{{\beta }_{2}}} \right|} } {{{{\left( {{{k}_{0}}{{n}_{2}}{{I}_{T}}} \right)}}^{{3{\text{/}}2}}}}}} \right. \kern-0em} {{{{\left( {{{k}_{0}}{{n}_{2}}{{I}_{T}}} \right)}}^{{3{\text{/}}2}}}}},$ $\tilde {W}\left( x \right)$ – функция Ламберта [32].

Рассмотрим вопрос устойчивости стационарного решения (21), (22) системы (14)–(17). Следуя методу Ляпунова [33], получаем четыре собственных значения

(24)
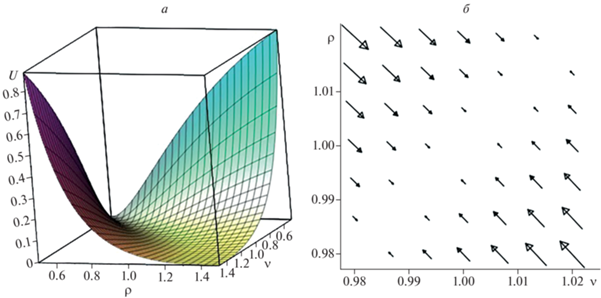
$\lambda = \pm \sqrt {\frac{{ - \left( {{{U}_{{,\nu \nu }}}{{m}_{2}} - d{{m}_{1}}} \right) \pm \sqrt {{{{\left( {{{U}_{{,\nu \nu }}}{{m}_{2}} - d{{m}_{1}}} \right)}}^{2}} - 4{{m}_{1}}{{m}_{2}}\left( {h{{U}_{{,\nu \rho }}} - d{{U}_{{,\nu \nu }}}} \right)} }}{{2{{m}_{1}}{{m}_{2}}}}} .$
Здесь нижние индексы после запятой обозначают производную по соответствующим переменным, $h = {{\tilde {F}}_{{,\nu }}} - {{U}_{{,\nu \rho }}},$ $d = {{\tilde {F}}_{{,\rho }}} - {{U}_{{,\rho \rho }}}.$ Стационарное решение будет устойчивым, если $\lambda $ не имеет положительной действительной части. Легко показать, что $\lambda $ будет чисто мнимой, если выполняются условия

(25)
$h{{U}_{{,\nu \rho }}} - d{{U}_{{,\nu \nu }}} > 0,$
(26)
${{U}_{{,\nu \nu }}}{{m}_{2}} - d{{m}_{1}} > 0.$

Равенство нулю действительной части означает, что вследствие малых возмущений параметры сигнала будут осциллировать в окрестности стационарных значений. Если убрать ионизационное слагаемое $\left( {\tilde {F} = 0} \right),$ то (25), (26) можно записать в виде условия минимума ${{U}_{{,\nu \nu }}}{{U}_{{,\rho \rho }}} - {{\left( {{{U}_{{,\nu \rho }}}} \right)}^{2}} > 0,$ ${{U}_{{,\nu \nu }}} > 0.$ Как и следовало ожидать, потенциальная функция в этом случае не имеет минимума. На рис. 1а представлен вид потенциальной поверхности $U$ без учета ионизации, а на рис. 1б соответствующее векторное поле ${{F}_{\nu }},$ ${{F}_{\rho }}.$ Если же учесть ионизацию, то в рамках используемого приближения (${{{{I}_{T}}} \mathord{\left/ {\vphantom {{{{I}_{T}}} {{{I}_{0}}}}} \right. \kern-0em} {{{I}_{0}}}} \gg 1$) условия (25), (26) выполняются при любых интенсивностях. Этот результат согласуется с полученным ранее в работе [34] выводом для планарных сигналов, в которой была использована линейная аппроксимация формулы Келдыша в туннельном пределе. Следует отметить, что при рассмотрении вопроса устойчивости мы пренебрегли смещением частоты сигнала. Учет этого эффекта привел бы к выводу систему из равновесия. Однако, поскольку смещение частоты входит в систему уравнений на параметры сигнала через высшую дисперсию $\left( {{{\beta }_{3}}} \right)$ и нелинейность $\left( {{\gamma \mathord{\left/ {\vphantom {\gamma \omega }} \right. \kern-0em} \omega }} \right)$ [34], то этой дестабилизацией на начальном этапе динамики можно пренебречь. Кроме того, как было показано в работах [28, 35, 36], поглощение, вызванное ионизацией, приводит к тому, что сигнал распространяется в режиме световой пули на расстояниях порядка нескольких миллиметров в диэлектрике.

Рис. 1.

Потенциальное поле $U\left( {\nu ,\rho } \right),$ определяющее динамику относительной длительности $\nu $ и ширины $\rho $ планарной пули (без вклада ионизации ${{L}_{\eta }} = \infty $) (а). Соответствующее поле сил, проекции, которых определяются выражениями ${{F}_{\nu }} = {{ - \partial U} \mathord{\left/ {\vphantom {{ - \partial U} {\partial \nu }}} \right. \kern-0em} {\partial \nu }},$ ${{F}_{\rho }} = {{ - \partial U} \mathord{\left/ {\vphantom {{ - \partial U} {\partial \rho }}} \right. \kern-0em} {\partial \rho }}$ (б).

Исследуем область интенсивностей, удовлетворяющую условию (23), в зависимости от центральной длины волны сигнала. В качестве материала возьмем сапфир. Для сапфира (${{U}_{I}} = 7.3\,\,{\text{эВ}},$ $~{{N}_{0}} = 2.36 \cdot {{10}^{{28}}}\,\,{{{\text{м}}}^{{ - 3}}},$ ${{\tau }_{c}} = 1.59 \cdot {{10}^{{ - 15{\text{\;}}}}}\,\,{\text{c}}$) приближенная зависимость показателя преломления от длины волны в среднем инфракрасном диапазоне может быть записана в виде [37]

(27)
${{n}_{0}} = 1.75\sqrt {1 + \frac{{1.73{{{\left( {\lambda [{\text{мкм}}]} \right)}}^{2}}}}{{{{{\left( {\lambda [{\text{мкм}}]} \right)}}^{2}} - {{{18}}^{2}}}}} ,$
а коэффициент ДГС определятся следующей зависимостью

(28)
${{\beta }_{2}} = \frac{{{{\lambda }^{3}}}}{{2\pi {{c}^{2}}}}\frac{{{{d}^{2}}{{n}_{0}}}}{{d{{\lambda }^{2}}}}.$

Нелинейный показатель преломления аппроксимируется выражением [38]

(29)
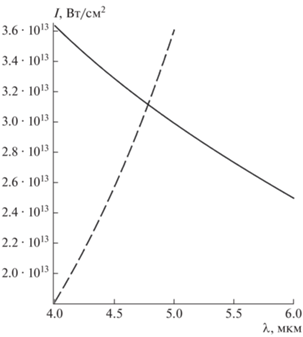
$\begin{gathered} {{n}_{2}} = n_{2}^{0} + {{N}_{1}}\exp \left( { - \frac{{\left( {\lambda - {{\lambda }_{0}}} \right)}}{{{{\lambda }_{1}}}}} \right) + \\ + \,\,{{N}_{2}}\exp \left( { - \frac{{\left( {\lambda - {{\lambda }_{0}}} \right)}}{{{{\lambda }_{2}}}}} \right). \\ \end{gathered} $
Здесь $n_{2}^{0}\, = \,2.5\, \cdot \,{{10}^{{ - 16}}}\,{{{\text{с}}{{{\text{м}}}^{2}}} \mathord{\left/ {\vphantom {{{\text{с}}{{{\text{м}}}^{2}}} {{\text{Вт}}}}} \right. \kern-0em} {{\text{Вт}}}}{\text{,}}$ ${{N}_{1}}\, = \,2.3 \cdot {{10}^{{ - 16}}}\,\,{{{\text{с}}{{{\text{м}}}^{2}}} \mathord{\left/ {\vphantom {{{\text{с}}{{{\text{м}}}^{2}}} {{\text{Вт}}}}} \right. \kern-0em} {{\text{Вт}}}}{\text{,}}$ ${{N}_{2}}\, = \,1.0 \cdot {{10}^{{ - 16}}}\,{{{\text{с}}{{{\text{м}}}^{{\text{2}}}}} \mathord{\left/ {\vphantom {{{\text{с}}{{{\text{м}}}^{{\text{2}}}}} {{\text{Вт}}}}} \right. \kern-0em} {{\text{Вт}}}},$ ${{\lambda }_{0}} = 266.0~\,\,{\text{нм,}}$ ${{\lambda }_{1}}\, = \,46.6\,~{\text{нм,}}$ ${{\lambda }_{2}} = 1086.3~\,\,{\text{нм}}{\text{.}}$ Подставляя (27)–(29) в (23), находим искомую зависимость (рис. 2). Для области, лежащей правее пунктирной линии выполняется условие $\omega {{\tau }_{p}} > 10,$ при котором справедливо используемое в работе приближение медленно меняющейся огибающей. Взяв ${{I}_{0}} = 2.8 \cdot {{10}^{{13}}}\,\,{{{\text{Вт}}} \mathord{\left/ {\vphantom {{{\text{Вт}}} {{{{\text{м}}}^{2}}}}} \right. \kern-0em} {{{{\text{м}}}^{2}}}},$ $\lambda = 5\,\,{\text{мкм}},$ из (21), (22) находим оценки для параметров планарного импульса: ${{\tau }_{0}} = 30\,\,{\text{фс}},$ $a = 10\,\,{\text{мкм}}.$

Рис. 2.

Сплошная линия описывается правой частью условия (23), которое определяет верхнюю границу интенсивности для существования стационарного решения в сапфире. Область правее пунктирной линии, определяющей интенсивность по формуле (21) для случая ${{\tau }_{p}}\omega = 10,$ соответствует области применимости метода медленно меняющейся огибающей $\left( {{{\tau }_{p}}\omega \geqslant 10} \right).$

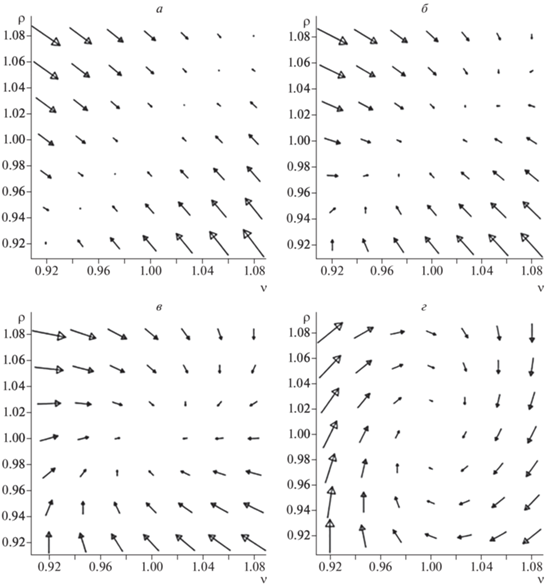
Выше мы получили, что условия устойчивости планарной пули относительно возмущений ее длительности и ширины (25), (26) выполняются для любых интенсивностей. Это означает, что при малых отклонениях частицы из положения равновесия (мы используем механическую аналогию) на нее действуют возвращающие силы, направленные в точку равновесия $\nu = 1,$ $\rho = 1.$ Из анализа векторного поля (с учетом ионизации) можно видеть (см. рис. 3), что возвращающие силы уменьшаются по экспоненциальному закону при уменьрис. 3а) возвращающие силы таковы, что векторное поле напоминает векторное поле для случая без ионизации (рис. 1). Таким образом, хотя формально условия устойчивости при такой интенсивности выполнены и возвращающие силы не равны нулю, фактически небольшие возмущения, связанные с эффектами, которыми мы пренебрегли, быстро выбьют систему из равновесия. Из анализа векторного поля можно предположить, что квазиустойчивость планарной пули при длине волны $\lambda = 5\,\,{\text{мкм}}$ можно ожидать начиная с интенсивности ${{I}_{0}} = 2 \cdot {{10}^{{13}}}\,\,{{{\text{Вт}}} \mathord{\left/ {\vphantom {{{\text{Вт}}} {{\text{с}}{{{\text{м}}}^{2}}}}} \right. \kern-0em} {{\text{с}}{{{\text{м}}}^{2}}}}.$ Схожая ситуация наблюдалась при исследовании области устойчивости трехмерных световых пуль [39]. В отличие от планарной пули область устойчивости трехмерной пули ограничена и снизу по интенсивности. Здесь мы также проводили анализ векторного поля и показали, что фактическая область устойчивости (ввиду влияния эффектов поглощения и слагаемых следующего порядка малости) лежит выше нижней границы формального окна устойчивости.

Рис. 3.

Векторное поле ${{F}_{\nu }} = {{ - \partial U} \mathord{\left/ {\vphantom {{ - \partial U} {\partial \nu }}} \right. \kern-0em} {\partial \nu }},$ ${{F}_{\rho }} = {{ - \partial U} \mathord{\left/ {\vphantom {{ - \partial U} {\partial \rho + \tilde {F}}}} \right. \kern-0em} {\partial \rho + \tilde {F}}}$ (с учетом ионизации), определяющее динамику планарного импульса с центральной длиной волны $\lambda = 5\,\,{\text{мкм}},$ распространяющегося в сапфире, с интенсивностью I0 = 1.5 · 1013 (а), 2 · 1013 (б), 2.3 · 1013 (в), 2.8 · 1013 Вт/см2 (г).

ЗАКЛЮЧЕНИЕ

Получено аналитическое описание распространения планарных импульсов в режиме взаимной компенсации эффектов дифракции и ионизационной расходимости, с одной стороны, и самофокусировки, с другой. Баланс временной динамики обуславливался компенсацией дисперсионного уширения кубической нелинейностью. С помощью метода моментов проанализирована динамика планарного сигнала в режиме туннельной ионизации. Получены аналитические выражения для квазистаионарных длительности и ширины планарного импульса. С помощью метода Ляпунова найдены условия квазиустойчивого распространения. Следует отметить, что учет смещения частоты в красную область спектра за счет явления вынужденного комбинационного саморассеяния или в синюю, если преобладают эффекты ионизации, будет приводить к медленному выходу системы из баланса и возникновению осцилляций. Кроме того, равновесие будет нарушаться и за счет поглощения фотонов в процессе ионизации, которым мы пренебрегли в данном исследовании. Поэтому равновесие, исследованное в работе, имеет квазиустойчивый характер.

Работа Халяпина В.А. выполнена при финансовой поддержке гранта Министерства науки и высшего образования РФ (проект № 075-02-2021-1748).

Список литературы

  1. Rairoux P., Schillinger H., Niedermeier S. et al. // Appl. Phys. B. 2000. V. 71. P. 573.

  2. Diels J.-C., Bernstein R., Stahlkopf K. et al. // Sci. Amer. 1997. V. 277. P. 50.

  3. Alfano R.R. The supercontinuum laser source. N.Y.: Springer, 1989. 538 p.

  4. D’Amico C., Houard A., Franco M. et al. // Phys. Rev. Lett. 2007. V. 98. Art. No. 235002.

  5. Kivshar Yu.S., Agrawal G.P. Optical solitons: from fibers to photonic crystals. N.Y.: Academic Press Inc., 2003. 540 p.

  6. Edmundson D.E., Enns R.H. // Opt. Lett. 1992. V. 17. P. 586.

  7. Mihalache D., Mazilu D., Crasovan L.-C. et al. // Phys. Rev. Lett. 2002. V. 88. Art. No. 073902.

  8. Fibich G., Ilan B. // Opt. Lett. 2004. V. 29. P. 887.

  9. Raghavan S., Agrawal Govind P. // 2000. V. 180. P. 377.

  10. Sazonov S.V., Kalinovich A.A., Komissarova M.V. et al. // Phys. Rev. A. 2019. V. 100. Art. No. 033835.

  11. Couairon A. // Eur. Phys. J. D. 1996. V. 27. P. 159.

  12. Henz S., Herrmann J. // Phys. Rev. E. 2006. V. 53. P. 4092.

  13. Sprangle P., Penano J.R., Hafizi B. // Phys. Rev. E. 2002. V. 66. Art. No. 046418.

  14. Sprangle P., Esarey E., Krall J. // Phys. Rev. E. 1996. V. 54. P. 4211.

  15. Penano J., Palastro J.P., Hafizi B. et al. // Phys. Rev. A. 2017. V. 96. Art. No. 013829.

  16. Couairon A., Mysyrowicz A. // Phys. Rep. 2007. V. 441. P. 47.

  17. Chekalin S.V., Dokukina E.A., Dormidonov A.E. et al. // J. Phys. B. 2015. V. 48. Art. No. 094 008.

  18. Воронин А.А., Желтиков А.М. // УФН. 2016. Т. 186. С. 957; Voronin A.A., Zheltikov A.M. // Phys. Usp. 2016. V. 59. P. 869.

  19. Saleh M.F., Chang W., Hölzer P. et al. // Phys. Rev. Lett. 2011. V. 107. Art. No. 203902.

  20. Hölzer P., Chang, W., Travers. J. et al. // Phys. Rev. Lett. 2011. V. 107. Art. No. 203901.

  21. Facao M., Carvalho M.I., Almeida P. // Phys. Rev. A. 2013. V. 87. Art. No. 063803.

  22. Дианов Е.М., Карасик А.Я., Мамышев П.В. // Письма в ЖЭТФ. 1985. Т. 41. № 6. С. 242; Dianov E.M., Karasik A.Y., Mamyshev P.V. et al. // JETP Lett. 1985. V. 41. No. 6. P. 294.

  23. Mitschke F.M., Mollenauer L.F. // Opt. Lett. 1986. V. 11. P. 659.

  24. Gordon J.P. // Opt. Lett. 1986. V. 11. P. 662.

  25. Santhanam J., Agraval G. // Opt. Commun. 2003. V. 222. P. 413.

  26. Bugay A.N., Khalyapin V.A. // Phys. Lett. A. 2017. V. 381. P. 399.

  27. Келдыш Л.В. // ЖЭТФ. 1964. Т. 47. С. 1945; Keldysh L.V. // Sov. Phys. JETP. 1965. V. 20. P. 1307.

  28. Залозная Е.Д., Дормидонов А.Е., Компанец В.О. и др. // Письма в ЖЭТФ. 2021. Т. 113. № 12. С. 817; Zaloznaya E.D., Dormidonov A.E., Kompanets V.O. et al. // JETP Lett. 2021. V. 113. No. 12. P. 817.

  29. Talepbour A., Yang J., Chin S.L. // Opt. Commun. 1999. V. 163. P. 29.

  30. Власов С.Н., Петрищев В.А., Таланов В.И. // Изв. вузов. Радиофиз. 1971. Т. 14. № 9. С. 1453.

  31. Маймистов А.И. // ЖЭТФ. 1993. Т. 104. № 5. С. 3620; Maimistov A.I. // JETP. 1993. V. 77. P. 727.

  32. Corless R., Gonnet G., Hare D.E.G. et al. // Adv. Comput. Math. 1996. V. 5. P.329.

  33. Ляпунов А.М. Общая задача об устойчивости движения. М.: Гостехиздат, 1950. 472 с

  34. Халяпин В.А., Бугай А.Н. // Изв. РАН. Сер. физ. 2021. Т. 85. № 12. С. 1781; Khalyapin V.A., Bugay A.N. // Bull. Russ. Acad. Sci. Phys. 2021. V. 85. No. 12. P. 1424.

  35. Дормидонов А.Е., Компанец В.О., Чекалин С.В. и др. // Квант. электрон. 2018. Т. 48. № 4. С. 372; Dormidonov A.E., Kompanets V.O., Chekalin S.V. et al. // Quantum Electron. 2018. V. 48. No. 4. P. 372.

  36. Bugay A.N., Khalyapin V.A. // Laser Phys. 2022. V. 32. Art. No. 025401.

  37. Malitson I.H. // J. Opt. Soc. Amer. 1962. V. 52. P. 1377.

  38. Major A., Yoshino F., Nikolakakos I. et al. // Opt. Lett. 2004. V. 15. P. 602.

  39. Bugay A.N., Khalyapin V.A. // Chaos Solitons Fractals. 2022. V. 156. Art. No. 111799.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал