1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 86, № 2, 2022

Известия РАН. Серия физическая, 2022, T. 86, № 2, стр. 194-198

Динамика трехмерных световых пуль в сверхрешетке с пространственно переменным показателем преломления

А. М. Белоненко 1, *, Ю. В. Двужилова 1, И. С. Двужилов 1, М. Б. Белоненко 1

1 Федеральное государственное автономное образовательное учреждение высшего образования “Волгоградский государственный университет”
Волгоград, Россия

* E-mail: arrow.doctor29@gmail.com

Поступила в редакцию 20.09.2021
После доработки 11.10.2021
Принята к публикации 22.10.2021

Полный текст (PDF)

Аннотация

Проведено численное моделирование динамики трехмерных световых пуль (предельно коротких оптических импульсов) в среде с пространственно-модулированным показателем преломления (в фотонном кристалле) на основе сверхрешетки из квантовых точек. Рассмотрена зависимость динамики импульсов от параметров фотонного кристалла (периода и глубины модуляции показателя преломления).

ВВЕДЕНИЕ

Нередко исследователи, которые работают в областях нелинейной оптики, нанофотоники и наноэлектроники пытаются решить одну из основных задач данных областей, основанную на новейших достижениях науки и техники в каждой области. Такой задачей является создание новых материалов, с помощью которых будет возможно управление параметрами оптических сигналов, уменьшение размеров структурных элементов устройств, а также создание на их основе системы передачи, обработки и хранения данных. Материалы, которые подлежат нашему исследованию – это сверхрешетки. Они представляют собой структуры, в которых помимо решетки есть искусственно созданный потенциал (с периодом, существенно превышающим период решетки), действующий на электроны. Таким образом, имеется возможность контроля зонного спектра [1].

Существует простейший способ создания сверхрешетки, которым мы и будем пользоваться. Данный способ заключается в образовании в твердом теле – кристалле периодической системы квантовых ям, которые связываются за счет туннельного эффекта, и в результате образуются коллективизированные состояния электронов с тем или иным законом дисперсии. В данном случае появляется возможность контролировать величину мини-зоны, благодаря изменению расстояния между квантовыми ямами.

Средой, которая подходит для образования сверхрешетки служит фотонный кристалл, имеющий пространственно-переменный показатель преломления. Выбор системы квантовых ям с туннелированием, как материала для фотонного кристалла обусловлен тем, что закон дисперсии электронов не описывается параболой, таким образом возникает нелинейный отклик на электромагнитные импульсы с напряженностью от 1000 до 10 000 В/см [2, 3]. Следует заметить, что неоднородность, возникающая в фотонном кристалле, является подходящей средой для исследования предельно коротких оптических импульсов (ПКОИ), световых пуль и других солитоноподобных состояний [4, 5].

Остановим свое внимание на трехмерных ПКОИ, которые представляют собой солитоноподобные импульсы, энергия которых локализована в пространстве. Длительность таких импульсов составляет несколько пикосекунд (1–5 колебаний электрического поля) [6].

Исследования распространения электромагнитных импульсов в фотонных кристаллах имеет большую теоретическую и практическую значимость в современной нелинейной оптике и нанофотонике, таким образом, задача, рассмотренная в настоящей работе, является весьма актуальной [7].

ФИЗИЧЕСКАЯ МОДЕЛЬ И ОСНОВНЫЕ УРАВНЕНИЯ

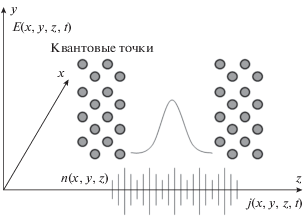
Геометрия задачи (рис. 1): вектор-потенциал электрического поля ПКОИ и ток направлены вдоль оси OY, а направление распространения импульса – оси OZ. Квантовые точки образуют систему квантовых ям, помещенных в фотонный кристалл. Предполагается, что туннелирование между квантовыми ямами вдоль осей OX и OZ мало, и им можно пренебречь.

Рис. 1.

Геометрия задачи.

Закон дисперсии для электронов в сверхрешетке:

(1)
$\varepsilon (p) = {{t}_{0}}2t\cos (bp),$
где p – момент импульса, который направлен вдоль оси OY, а b – расстояние между соседними квантовыми ямами (вдоль оси OY), t0 – энергия электронов в квантовой яме, t – туннельный интеграл перекрывания, действующий в соседних квантовых ямах.

Закон дисперсии (1) может быть записан в условиях электрон-электронного и электрон-фотонного взаимодействия, если понимать t0 и t, как соответствующие перенормированные константы.

С помощью уравнений Максвелла, используя калибровку Кулона (E = –∂A/c∂t), уравнение на вектор-потенциал электромагнитного поля световой пули, распространяющейся внутри сверхрешетки с пространственно переменным показателем преломления, будет иметь вид [8]:

(2)
$\frac{{{{\partial }^{2}}\vec {A}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}\vec {A}}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}\vec {A}}}{{\partial {{z}^{2}}}} - \frac{{{{n}^{2}}\left( {x,y,z} \right)}}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}\vec {A}}}{{\partial {{t}^{2}}}} + \frac{{4\pi }}{c}\vec {j} = 0.$
здесь $\vec {A}$ = (0, A(x, y, z, t),0) – вектор-потенциал электрического поля импульса, $\vec {j}$ = (0, j(x, y, z, t),0) – плотность электрического тока, n(x, y, z) – пространственное изменение показателя преломления, с – скорость света [9].

В данной работе использованы следующие приближения: во-первых, начальные условия по оси z выбираются однородными; во-вторых, эффекты, связанные с неоднородностью электромагнитного поля вдоль этой оси, не учитывались. Это связано с тем, что типичное время релаксации для электронов можно оценить, как 10–12–10–13 с [10]. Таким образом, в уравнении (2) мы пренебрегли слагаемым, отвечающим за неоднородность функции распределения электронов вдоль оси z. Такие приближения оправданы тем, что волновой фронт лазерного излучения однороден.

Воспользуемся кинетическим уравнением Больцмана для описания эволюции электронов в сверхрешетке:

(3)
$\frac{{\partial f}}{{\partial t}} - \frac{q}{c}\frac{{\partial {{A}_{z}}}}{{\partial t}}\frac{{\partial f}}{{\partial p}} = \frac{{{{F}_{0}} - f}}{\tau }.$
здесь f – функция распределения электронов, F0 – функция распределения Ферми, τ – время релаксации.

Плотность электрического тока, возникающего в сверхрешетке имеет вид [3]:

(4)
$j = 2e\sum\limits_{s = 1}^m {\int\limits_{ZB} {{{\nu }_{s}}\left( p \right)f\left( {p,s} \right)dp} } ,$
где νs(p) = (∂εs(p))/∂p – групповая скорость электронов, εs(p) – закон дисперсии, описывающий электронные свойства системы квантовых ям (формула (1)), e – заряд электрона, ZB – первая зона Бриллюэна.

С учетом формулы для плотности тока (уравнение 4) можно получить обобщенное уравнение синус-Гордона [12], описывающее динамику трехмерного ПКОИ в фотонном кристалле со сверхрешеткой:

(5)
$\begin{gathered} \frac{{{{\partial }^{2}}A}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}A}}{{\partial {{y}^{2}}}} - \frac{{{{n}^{2}}(x,y,z)}}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}A}}{{\partial {{t}^{2}}}} + \frac{{qb}}{{\pi h\tau }}\sin \left( {\frac{{aq}}{c}A} \right) = 0, \\ b = \int\limits_{ - q0}^{q0} {dp \cdot \cos \left( {ap} \right){{F}_{0}}\left( p \right)} , \\ {{F}_{0}}\left( p \right) = \frac{1}{{1 + \exp \left\{ {{{\varepsilon \left( p \right)} \mathord{\left/ {\vphantom {{\varepsilon \left( p \right)} {{{k}_{b}}T}}} \right. \kern-0em} {{{k}_{b}}T}}} \right\}}}, \\ \end{gathered} $
где kb – постоянная Больцмана, Т – температура.

Подробный вывод уравнения (6) показан в более ранних работах авторов [13].

В работе [14] показано, что трехмерная задача о распространении предельно короткого оптического импульса является цилиндрически симметричной. Это связано с тем, что эффектом накопления заряда можно пренебречь.

Таким образом, эффективное уравнение на вектор-потенциал А электромагнитного поля световой пули в цилиндрически симметричном случае примет вид:

(6)
$\begin{gathered} \frac{{{{\partial }^{2}}A}}{{\partial {{z}^{2}}}} + \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial A}}{{\partial r}}} \right) - \frac{{{{n}^{2}}(z,r)}}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}A}}{{\partial {{t}^{2}}}} + \\ + \,\,\,\frac{{qb}}{{\pi h\tau }}\sin \left( {\frac{{aq}}{c}A} \right) = 0,\,\,\,r = \sqrt {{{x}^{2}} + {{y}^{2}}} . \\ \end{gathered} $

Коэффициенты разложения b показаны в уравнении (5).

Начальные условия на вектор-потенциал ПКОИ имеют вид:

(7)
$\begin{gathered} {{А}_{{t = 0}}} = {{A}_{0}}\exp \left\{ { - \frac{{{{r}^{2}}}}{{{{\gamma }^{2}}}}} \right\}\exp \left\{ { - {{{{{\left( {z - {{z}_{c}}} \right)}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left( {z - {{z}_{c}}} \right)}}^{2}}} {{{\beta }^{2}}}}} \right. \kern-0em} {{{\beta }^{2}}}}} \right\}, \\ {{\left. {\frac{{dА}}{{dt}}} \right|}_{{t = 0}}} = \frac{{2vz}}{{{{\gamma }^{2}}}}{{A}_{0}}\exp \left\{ { - \frac{{{{r}^{2}}}}{{{{\gamma }^{2}}}}} \right\}\exp \left\{ { - {{{{{\left( {z - {{z}_{c}}} \right)}}^{2}}} \mathord{\left/ {\vphantom {{{{{\left( {z - {{z}_{c}}} \right)}}^{2}}} {{{\beta }^{2}}}}} \right. \kern-0em} {{{\beta }^{2}}}}} \right\}. \\ \end{gathered} $

Показатель преломления фотонного кристалла со сверхрешеткой на основе квантовых точек задан следующим образом:

(8)
$n(z,r) = {{n}_{0}}(1 + \alpha \cos ({{2\pi z} \mathord{\left/ {\vphantom {{2\pi z} {\chi )).}}} \right. \kern-0em} {\chi )).}}$
Здесь β, γ – параметры, определяющие ширину импульса по осям z и r соответственно, t0 – начальный момент времени, ν – начальная скорость импульса, α – глубина модуляции показателя преломления, χ – период модуляции показателя преломления.

РЕЗУЛЬТАТЫ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ

Уравнение для эволюции трехмерного ПКОИ (6) решалось с помощью явной численной схемы типа “крест” [15].

Эволюция импульса электромагнитного поля при его распространении в среде из квантовых точек (сверхрешетке) с пространственно переменным показателем преломления (фотонном кристалле), в случае одного колебания электрического поля представлена на рис. 2.

Рис. 2.

Динамика трехмерного ПКОИ в фотонном кристалле со сверхрешеткой, в различные моменты времени (параметры модуляции показателя преломления: глубина модуляции α = 0.1; период модуляции χ = 2.5 мкм): 2 (а), 4 (б), 8 (в), 12 пс (г).

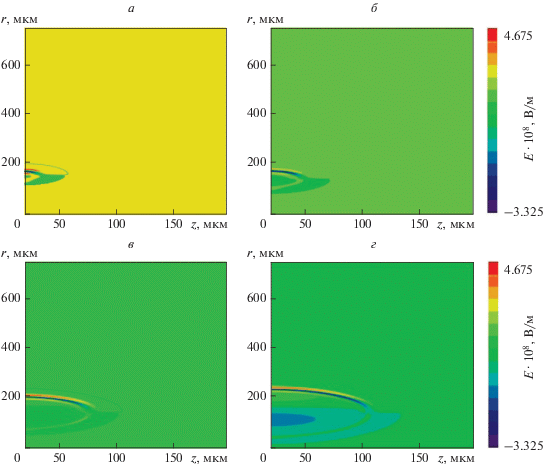
Из рис. 2, можно сделать вывод о том, что имеет место дифракционное и дисперсионное расширение импульса. Но импульс остается, локализован в пределах ограниченной области.

Эволюция трехмерного предельно короткого оптического импульса, в момент времени 4 пс, в фотонном кристалле со сверхрешеткой, с различными параметрами фотонного кристалла представлена на рис. 3.

Рис. 3.

Динамика трехмерного ПКОИ в фотонном кристалле со сверхрешеткой, в момент времени 4 пс, с различными значениями глубины модуляции показателя преломления, при фиксированном периоде модуляции χ = 2.5 мкм: α = = 0.3 (а), 0.7 (б), с различными значениями параметра модуляции показателя преломления α = 0.3: χ = 25 (в), 75 (г).

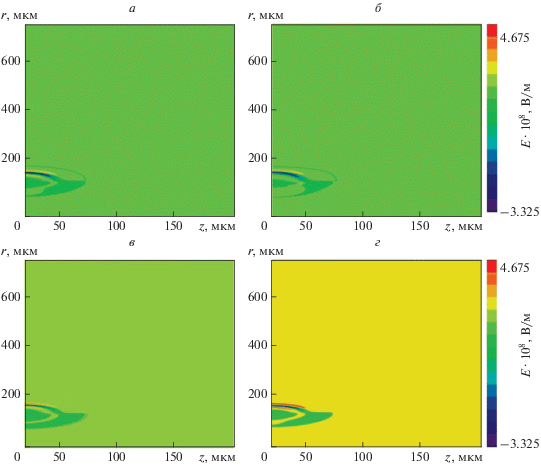
Из рис. 3 видно, что, изменение глубины модуляции показателя преломления и форма импульса меняется незначительно, чем можно в дальнейших исследованиях пренебречь, помимо этого энергия этого импульса остается в ограниченной пространственной области.

Варьируя, в свою очередь, период модуляции показателя преломления можно контролировать групповую скорость предельно короткого оптического импульса. Причем, чем больше период, тем скорость выше. Это обусловлено тем, что процессы отражения и интерференции происходят реже.

Следует отметить, что при распространении трехмерного ПКОИ в среде с пространственно переменным показателем преломления (фотонном кристалле на основе сверхрешетки) имеет место возбуждение внутренних колебательных мод, и, в связи с этим, импульс приобретает сложную поперечную структуру при распространении. Такой эффект связан с тем, что во время прохождения среды фотонного кристалла импульс взаимодействует с неоднородностью показателя преломления.

Влияние параметров фотонного кристалла на форму и групповую скорость волнового пакета предельно короткого импульса было неоднократно проверено для предельно коротких импульсов и световых пуль различных начальных форм [16–18].

ЗАКЛЮЧЕНИЕ

На основании уравнений Максвелла, в калибровке Кулона, описывающих динамику предельно коротких оптических импульсов в фотонном кристалле, с трехмерной сверхрешеткой, связанных сильным туннелированием вдоль одной оси, получено феноменологическое уравнение в форме классического (2 + 1)-мерного уравнения синус-Гордон с переменными коэффициентами для случая цилиндрической симметрии. Установлено устойчивое распространение трехмерных световых пуль в фотонном кристалле со сверхрешеткой на основе квантовых ям, которые связаны туннелированием. Энергия импульса остается сосредоточенной в ограниченной области пространства, однако, вследствие дисперсионных эффектов имеет место незначительное изменение формы световой пули. Параметры фотонного кристалла (период и глубина модуляции показателя преломления) оказывают влияние на групповую скорость волнового пакета импульса и его форму.

Полученные результаты могут быть использованы для решения актуальных задач современной нелинейной оптики и нанофотоники.

А.М. Белоненко, Ю.В. Двужилова и И.С. Двужилов выражают благодарность Министерству науки и высшего образования Российской Федерации и Совету по грантам Президента РФ (проект МК-2089.2021.1.2).

Список литературы

  1. Басс Ф.Г., Булгаков А.А., Тетервов А.П. Высокочастотные свойства полупроводников со сверхрешетками. М.: Наука, 1989. 286 с.

  2. Двужилов И.С., Двужилова Ю.В., Белоненко М.Б. // Опт. и спектроск. 2021. Т. 129. № 1. С. 92.

  3. Belonenko M., Demushkina E.V., Lebedev N.G. // J. Russ. Las. Res. 2006. V. 27. P. 457.

  4. Zhukov A.V., Bouffanais R., Belonenko M.B. et al. // Eur. Phys. J. D. 2015. V. 69. P. 242.

  5. Mekis A., Chen J.C., Kurland I. et al. // Phys. Rev. Lett. 1996. V. 77. P. 3787.

  6. Tokushima M., Kosaka H., Tomita A. et al. // Appl. Phys. Lett. 2000. V. 76. P. 952.

  7. Goorjian P.M., Silberberg Y. // J. Opt. Soc. Amer. B. 1997. V. 14. P. 3253.

  8. Fedorov, E.G. Zhukov A.V., Bouffanais R. et al. // Opt. Expr. 2019. V. 27. No. 20. Art. No. 27592.

  9. Белоненко М.Б., Мостовая Е.И. // Опт. и спектроск. 2019. Т. 126. № 5. С. 563.

  10. Ландау Л.Д., Лифшиц Е.М. Теория поля. М: Наука, 1988.

  11. Grahn H.T., Klitzing K., Ploog K. et al. // Phys. Rev. B. 1991. V. 43. Art. No. 12095.

  12. Li P., Mihalache D., Malomed B.A. // Phil. Trans. R. Soc. A. 2018. V. 376 (2124). Art. No. 20170378.

  13. Belonenko M.B., Meshcheryakova N.E. // J. Russ. Las. Res. 2008.V. 29. No. 1. P. 49.

  14. Zhukov A.V., Bouffanais R., Fedorov E.G. et al. // J. Appl. Phys. 2013. V. 114. Art. No. 143106.

  15. Бахвалов Н.С. Численные методы (анализ, алгебра, обыкновенные дифференциальные уравнения). М.: Наука, 1975. 632 с.

  16. Belonenko M.B., Dvuzhilov I.S., Tuzalina O.Yu. // J. Nano-Electron. Phys. 2015. V. 7. No. 4. Art. No. 04013.

  17. Belonenko M.B., Dvuzhilov I.S., Galkina E.N. et al. // Mod. Phys. Lett. B. 2016. V. 30. Art. No. 1650345.

  18. Dvuzhilova Y.V., Dvuzhilov I.S., Ten A.V. et al. // Mod. Phys. Lett. B. 2019. V. 33. No. 23. Art. No. 1950275.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал