1. На главную
  2. Электронные версии
  3. Известия РАН. Серия физическая
  4. T. 86, № 2, 2022

Известия РАН. Серия физическая, 2022, T. 86, № 2, стр. 182-186

Фазовые переходы в антиферромагнитной модели Изинга с конкурирующими обменными взаимодействиями в магнитном поле

К. Ш. Муртазаев 1, *, А. К. Муртазаев 2, М. К. Рамазанов 1, 2, М. А. Магомедов 1, 2

1 Федеральное государственное бюджетное учреждение науки “Институт физики имени Х.И. Амирханова” Дагестанского федерального исследовательского центра Российской академии наук
Махачкала, Россия

2 Федеральное государственное бюджетное учреждение науки Дагестанский федеральный исследовательский центр Российской академии наук
Махачкала, Россия

* E-mail: 5kurban@mail.ru

Поступила в редакцию 20.09.2021
После доработки 11.10.2021
Принята к публикации 22.10.2021

Полный текст (PDF)

Аннотация

Высокоэффективным репличным алгоритмом метода Монте-Карло исследована трехмерная антиферромагнитная Изинговская модель на объемно-центрированной кубической решетке с конкурирующими обменными спиновыми взаимодействиями во внешнем магнитном поле. Проведен анализ фазовых переходов. Показано, что сильное магнитное поле приводит к подавлению фазового перехода.

ВВЕДЕНИЕ

В настоящее время работы по изучению фазовых переходов (ФП), магнитных и термодинамических свойств модельных спиновых систем с конкурирующими обменными взаимодействиями представляют большой интерес в физике конденсированного состояния. Конкуренция обменных взаимодействий в магнитных спиновых системах может привести к возникновению фрустраций. Свойства и параметры фрустрированных спиновых систем сильно отличаются от свойств аналогичных систем без фрустраций. Спиновые системы с фрустрациями имеют большое разнообразие фаз и фазовых переходов. Такое разнообразие ФП обусловлено сильным вырождением таких систем и их высокой чувствительностью к различным внешним факторам. Внешнее магнитное поле, как внешний фактор, может привести к новым физическим явлениям в поведении фрустрированных и спиновых систем с конкурирующими обменными взаимодействиями [1–6].

В данном исследовании нами рассматривается трехмерная (3D) антиферромагнитная Изинговская объемно-центрированная кубическая (ОЦК) решетка с конкурирующими обменными спиновыми взаимодействиями. Будет изучено влияние магнитного поля на магнитные и термодинамические свойства рассматриваемой модели и характер ФП.

Изинговская модель с конкуренцией обменных спиновых взаимодействий на разных типах решеток исследована достаточно хорошо. Результаты численных расчетов и теоретических исследований в рассматриваемой модели приведены в работах [6–9]. В исследованиях, представленных в работе [6] авторы получили структуры подрешеток в основном состоянии для 3D антиферромагнитной Изинговской модели на ОЦК решетке с помощью алгоритма Ванга–Ландау метода Монте-Карло (МК). Авторами работы на фазовой диаграмме были обнаружены области, где реализуются фазовые переходы первого рода и второго рода. Результаты теоретических исследований, представленные в работе [7] показывают, что для Изинговской ОЦК решетки реализуется ФП II рода. Этот результат имеет хорошее согласие с данными, полученными в работе [6]. Влияние магнитного поля на род фазового перехода и термодинамические свойства для рассматриваемой Изинговской модели со значениями магнитного поля 0.0 ≤ H ≤ 6.0 исследовано в работе [8]. Обнаружено, что в рассмотренном интервале H наблюдается ФП второго рода. В работе [9] для антиферромагнитной Изинговской модели на слоистой треугольной решетке показано, что при значениях магнитных полей 0.0 ≤ H ≤ 6.0 наблюдается ФП второго рода. Обнаружено, что сильные магнитные поля снимают вырождение основного состояния и приводят размыванию ФП.

Анализ литературных данных показывает, что многие физические свойства спиновых систем с конкуренцией обменных спиновых взаимодействий зависят от наличия или отсутствия внешнего магнитного поля [10–12]. Поэтому, нами проводится численный расчет по исследованию ФП и термодинамических свойств 3D антиферромагнитной Изинговской модели на ОЦК решетке в сильных магнитных полях. Интерес к данным исследованиям объясняется еще тем, что большинство подобных работ посвящены моделям на гексагональных треугольных и квадратных решетках [13–23]. Исследование данной спиновой системы на основе эффективных и современных алгоритмов позволит ответить на ряд существующих вопросов, связанных с влиянием магнитного поля на термодинамические свойства и фазовые переходы спиновых решеточных систем с конкурирующими обменными взаимодействиями. Актуальность исследования влияния магнитного поля на ФП обусловлена еще и тем, что в современной микроэлектронике (и спинтронике) невозможно пренебречь влиянием внешних факторов на поведение приборов и элементов электроники. Уровень миниатюризации современной микроэлектроники таков, что те факторы, которые раньше рассматривались как несущественные, сегодня не могут быть игнорированы.

МОДЕЛЬ И МЕТОДИКА ИССЛЕДОВАНИЯ

Гамильтониан описывающую данную спиновую систему имеет следующий вид:

(1)
${\rm H} = - {{J}_{1}}\sum\limits_{\left\langle {i,j} \right\rangle } {{{S}_{i}}{{S}_{j}} - {{J}_{2}}} \sum\limits_{\left\langle {\left\langle {i,l} \right\rangle } \right\rangle } {{{S}_{i}}{{S}_{l}} - H} \sum\limits_i {{{S}_{i}}} ,$
где J1 и J2 – постоянные величины (константы) обменного спинового взаимодействия первых ближайших (J1= –1) и вторых (J2= –1) ближайших соседей(спинов), Si = ±1 – значение Изинговского спина, H – величина магнитного поля (приводится в единицах |J1|). Магнитное поля менялась в интервале 7.0 ≤ H ≤ 14.0.

Спиновые системы с конкуренцией спиновых обменных взаимодействий с помощью микроскопических гамильтонианов успешно исследуются на основе метода Монте-Карло (МК) [9, 11, 24–33]. В настоящее время расчеты проводятся на основе многих вариантов алгоритмов Монте-Карло метода. Одним из наиболее эффективных и точных для исследования и расчета подобных спиновых систем является репличный обменный алгоритм МК метода [34]. Поэтому для выполнения данного исследования нами используется репличный алгоритм Монте-Карло метода.

Репличный обменный алгоритм метода МК, который мы использовали можно описать в следующем виде:

1. Одновременно моделируются несколько Q копий (реплик) системы X1, X2, … XQ с температурами T1, T2, … TQ.

2. Для избавления от проблемы критического замедления системы после выполнения одного МК-шага/спин для всех копий реплик производится обмен конфигурациями (данными) между парой соседних реплик Xi и Xi + 1 с вероятностью:

$w({{X}_{i}} \to {{X}_{{i + 1}}}) = \left\{ \begin{gathered} \hfill 1,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{for}}\,\,\,\Delta \leqslant 0, \\ \hfill \exp ( - \Delta ),\,\,\,\,{\text{for}}\,\,\,\Delta > 0, \\ \end{gathered} \right.$
где $\Delta = \left( {{{U}_{i}} - {{U}_{{i + 1}}}} \right)\left( {{1 \mathord{\left/ {\vphantom {1 {{{T}_{i}}}}} \right. \kern-0em} {{{T}_{i}}}} - {1 \mathord{\left/ {\vphantom {1 {{{T}_{{i + 1}}}}}} \right. \kern-0em} {{{T}_{{i + 1}}}}}} \right),$ Ui и Ui + 1 – внутренние энергии реплик.

Расчеты проводились с использованием периодических граничных условий. Линейные размеры системы составляли 2 × L × L × L = N, L = 12–60, где N – количество спинов в системе, L – размер решетки. Для изучения типа ФП и определения критической температуры использовались гистограммный метод анализа данных и метод кумулянтов Биндера четвертого порядка [35, 36]. Для того, чтобы вывести систему в термодинамическое равновесие выделялся участок равный τ0 = 4 · 105 шагов МК на спин, что в несколько раз превосходит размер неравновесного участка. Усреднение термодинамических параметров проводилось вдоль марковской цепи длиной до τ = = 500τ0 шагов МК на спин.

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ НА ЭВМ

Расчет зависимости теплоемкости C от температуры производился с помощью следующего выражения:

(2)
$C = \left( {N{{K}^{2}}} \right)\left( {\left\langle {{{{\rm H}}^{2}}} \right\rangle - {{{\left\langle {\rm H} \right\rangle }}^{2}}} \right),$
где $K = {{\left| {{{J}_{1}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{J}_{1}}} \right|} {{{k}_{B}}T}}} \right. \kern-0em} {{{k}_{B}}T}}$ – обратная температуре величина, N – число частиц, H – оператор Гамильтониана.

Параметр порядка данной системы рассчитывался по следующей формуле [37]:

(3)
$m = 3{{m}_{1}} - {{m}_{2}} - {{m}_{3}} - {{m}_{4}},$
где ${{m}_{1}},{{m}_{2}},{{m}_{3}},{{m}_{4}}$ − параметры порядка по подрешеткам.

В данной системе сосуществуют 4 подрешетки. Более подробно про структуры подрешеток можно посмотреть в работе [6].

Для вычисления намагниченности использовалась формула:

(4)
$M = \frac{1}{N}\sum\limits_i {{{S}_{i}}} .$

Для определения типа ФП использовался метод кумулянтов Биндера UL четвертого порядка:

(5)
${{U}_{L}} = 1 - \frac{{{{{\left\langle {{{m}^{4}}} \right\rangle }}_{L}}}}{{\left\langle {3{{m}^{2}}} \right\rangle _{L}^{2}}}.$

Используя формулу (5) с высокой точностью можно найти критическую температуру TN, если в системе происходит фазовый переход II рода [10].

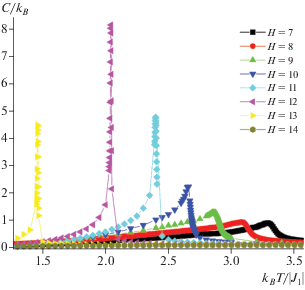
На рис. 1 показаны зависимости теплоемкости от температуры при L = 24 для разных значений величины магнитного поля. На рисунке отчетливо видно, что при значениях магнитного поля 7.0 ≤ H ≤ 10.0 с ростом значения H происходит смещение максимумов теплоемкости в область низких температур. Также на рисунке можно заметить рост значений максимумов теплоемкости. При значениях магнитного поля 11.0 ≤ H ≤ 13.0 в критической области наблюдаются более резкие пики. Можно предположить, что в этом интервале реализуется ФП первого рода. Мы предполагаем, что магнитное поле благоприятствует усилению конкурирующего спинового взаимодействия между первыми ближайшими и вторыми ближайшими соседями и в связи с этим наблюдается смещение максимумов теплоемкости в область низких температур. На рис. 1 видно, что для теплоемкости при значении магнитного поля H = 14 пик не наблюдается. Это говорит о том, что дальнейшее увеличение магнитного поля подавляет ФП.

Рис. 1.

Зависимость теплоемкости C/kB от температуры kBT/|J1|.

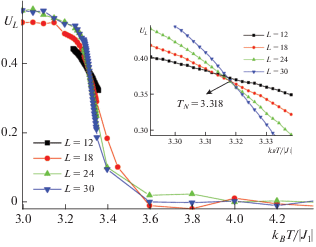
На рис. 2. представлены зависимости кумулянта Биндера четвертого порядка UL при значении магнитного поля H = 7.0 для разных размеров системы L. На графике видна отчетливая точка пересечения (TN = 3.318). Это говорит о том, что в системе реализуется фазовый переход II рода, а сама точка соответствует критической температуре. Аналогичные зависимости кумулянтов Биндера были построены и для значения магнитных полей 7.0 ≤ H ≤ 13.0. Анализ результатов показывает, что в интервале 7.0 ≤ H ≤ 10.0 наблюдается ФП второго рода. В интервале 11.0 ≤ H ≤ 14.0 на зависимостях кумулянтов Биндера не наблюдаются точки пересечения.

Рис. 2.

Зависимость кумулянта Биндера UL от температуры kBT/|J1| для разных L при H = 7.0.

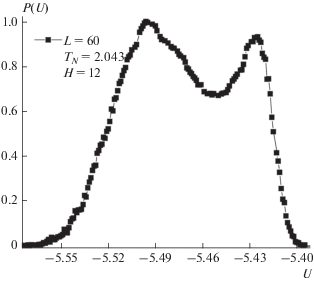
Анализ природы ФП был проведен используя гистограммный метод анализа данных. Гистограмма распределения энергии для спиновой системы с линейным размером L = 60 для поля H = 12.0 приведена на рис. 3. Как видно на графике, для поля H = 12.0 на гистограмме наблюдаются двойной максимум (два пика), который свидетельствует в пользу ФП I рода. Обнаружение двойного пика (бимодальность) на гистограммах распределение энергии говорит о том, что реализуется ФП I рода и является достаточным условием. Аналогичное поведение наблюдается в интервале значений поля 11.0 ≤ H ≤ 13.0.

Рис. 3.

Гистограмма распределения энергии для H = = 12.0.

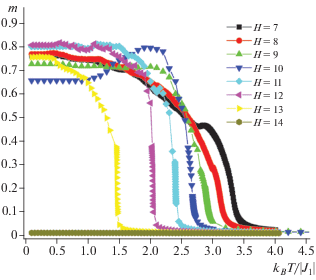
Температурные кривые магнитного параметра порядка m для различных значений H приведены на рис. 4. На рисунке видно, что с ростом H область спада магнитного параметра порядка сдвигается в сторону низких температур. Это объясняется тем, что магнитное поле усиливает конкурирующее спиновое взаимодействие между первыми соседями и вторыми ближайшими соседями. Для значений магнитных полей 11.0 ≤ H ≤ 13.0 наблюдаются более резкие спады параметра порядка. Такое поведение для температурных зависимостей магнитного параметра порядка является характерным для ФП первого рода.

Рис. 4.

Зависимость параметра порядка m от температуры kBT/|J1|.

Полученные результаты свидетельствуют, что в интервале значений поля 7.0 ≤ H ≤ 10.0 переход из антиферромагнитной фазы в парамагнитную происходит как ФП второго рода, а в интервале 11.0 ≤ H ≤ 13.0 наблюдается ФП первого рода. При дальнейшем росте значения магнитного поля подавляется фазовый переход.

ЗАКЛЮЧЕНИЕ

Изучена антиферромагнитная Изинговская модель на объемно-центрированной кубической решетке с конкуренцией обменных спиновых взаимодействий в сильных магнитных полях на основе репличного алгоритма МК метода. Рассмотрен интервал значений магнитного поля 7.0 ≤ H ≤ 14.0. Показано, что в диапазоне магнитного поля 7.0 ≤ ≤ H ≤ 10.0 происходит фазовый переход второго рода, а в диапазоне 11.0 ≤ H ≤ 13.0 фазовый переход первого рода

Исследование выполнено при финансовой поддержке РФФИ (проекты № 20-32-90079-аспиранты и № 19-02-00153-а) и Фонда развития теоретической физики и математики “БАЗИС”.

Список литературы

  1. Паташинский А.З., Покровский В.Л. Флуктуационная теория фазовых переходов. М.: Наука, 1982.

  2. Гехт Р.С. // УФН. 1989. Т. 159. С. 261.

  3. Katsumata K., Aruga Katori H., Kimura S. et al. // Phys. Rev. 2010. No. 82. Art. No. 104402.

  4. Ма Ш. Современная теория критических явлений. М.: Мир, 1980.

  5. Муртазаев А.К., Рамазанов М.К., Курбанова Д.Р., Бадиев М.К. // ФТТ. 2018. Т. 60. С. 1162.

  6. Murtazaev A.K., Ramazanov M.K., Kurbanova D.R. et al. // Mater. Lett. 2019. V. 236. P. 669.

  7. Муртазаев А.К., Рамазанов М.К., Кассан-Оглы Ф.А., Курбанова Д.Р. // ЖЭТФ. 2015. Т. 147. С. 127.

  8. Муртазаев А.К., Рамазанов М.К., Муртазаев К.Ш. и др. // ФТТ. 2020. Т. 62. С. 229.

  9. Murtazaev A.K., Badiev M.K., Ramazanov M.K., Magomedov M.A. // Physica A. 2020. V. 555. Art. No. 124530.

  10. Mengxing Ye, Chubukov A.V. // Phys. Rev. B. 2017. V. 95. Art. No. 014425

  11. Shun-Qing Shen, Zhang F.C. // Phys. Rev. B. 2002. V. 66. Art. No. 172407.

  12. Yamamoto D., Suzuki C., Marmorini G. et al. // Phys. Rev. Lett. 2020. V. 125. Art. No. 057204.

  13. Ramazanov M.K., Murtazaev A.K., Magomedov M.A. // Sol. St. Commun. 2016. V. 233. Art. No. 35.

  14. Муртазаев А.К., Магомедов М.А., Рамазанов М.К. // Письма в ЖЭТФ. 2018. Т. 107. С. 265.

  15. Рамазанов М.К., Муртазаев А.К. // Письма в ЖЭТФ. 2016. Т. 103. С. 522.

  16. Рамазанов М.К., Муртазаев А.К. // Письма в ЖЭТФ. 2017. Т. 106. С. 72.

  17. Рамазанов, М. К. Муртазаев А. К. // Письма в ЖЭТФ. 2019. Т. 109. С. 610.

  18. Murtazaev A.K., Ramazanov M.K., Badiev M.K. // Physica A. 2018. V. 507. Art. No. 210.

  19. Kassan-Ogly F.A., Murtazaev A.K., Zhuravlev A.K. et al. // J. Magn. Magn. Mater. 2015. V. 384. P. 247.

  20. Proshkin A.I., Kassan-Ogly F.A. // Mater. Sci. Forum. 2016. V. 845. P. 93.

  21. Kawamura H.J. // Phys. Soc. Japan. 1992. V. 61. Art. No. 1299.

  22. Mailhot A., Plumer M.L., Caille A. // Phys. Rev. 1994. V. 50. Art. No. 6854.

  23. Свистов Л.Е., Смирнов А.И., Прозорова Л.А. и др. // Письма в ЖЭТФ. 2004. Т. 80. С. 231.

  24. Masrour R., Jabar A., Benyoussef A., Hamedoun M. // J. Magn. Magn. Mater. 2016. V. 401. P. 695.

  25. Муртазаев А.К., Ризванова Т.Р., Рамазанов М.К., Магомедов М.А. // ФТТ. 2020. Т. 62. С. 1278.

  26. Муртазаев А.К., Кассан-Оглы Ф.А., Рамазанов М.К., Муртазаев К. Ш. // Физ. мет. и металловед. 2020. Т. 121. С. 346.

  27. Муртазаев А.К., Рамазанов М.К., Бадиев М.К. // Физ. низк. темп. 2019. Т. 45. С. 1493.

  28. Murtazaev A.K., Kurbanova D.R., Ramazanov M.K. // Physica A. 2020. V. 545. Art. No. 123548.

  29. Муртазаев А.К., Рамазанов М.К. // ФТТ. 2020. Т. 62. С. 868.

  30. Муртазаев А.К., Мазагаева М.К., Рамазанов М.К. и др. // ФТТ. 2020. Т. 63. С. 622.

  31. Murtazaev K.Sh., Murtazaev A.K., Ramazanov M.K. et al. // Low Temp. Phys. 2021. V. 47. P. 515.

  32. Бадиев М.К., Муртазаев А.К., Рамазанов М.К., Магомедов М.А. // Физ. низк. темп. 2020. Т. 46. С. 824.

  33. Wang F., Landau D.P. // Phys. Rev. E. 2001. V. 64. Art. No. 056101.

  34. Mitsutake A., Sugita Y., Okamoto Y. // Biopolymers. Peptide Sci. 2001. V. 60. P. 96.

  35. Binder K. // Z. Phys. 1981. V. 43. P. 119.

  36. Wang F., Landau D.P. // Phys. Rev. Lett. 2001. V. 86. Art. No. 2050.

  37. Landau D.P. // Phys. Rev. 1983. V. 27. Art. No. 5604.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал