Известия РАН. Серия физическая, 2022, T. 86, № 7, стр. 1031-1036

ВВЕДЕНИЕ

Интегралы от функций многих переменных встречаются во многих областях физики. Приведем примеры. Перенос нейтронов, фотонов и других частиц в среде описывается уравнением для функции распределения; эта функция зависит от трех координат среды и трех компонент вектора скорости частицы, то есть число переменных равно шести. Для определения коэффициентов теплопроводности или электропроводности среды приходится вычислять интегралы рассеяния; в них входят компоненты векторов скоростей двух частиц до момента столкновения и после момента столкновения. Общее число переменных в таком интеграле равно двенадцати. Возникают задачи и с существенно большим числом переменных.

В простейшей постановке рассматривают вычисление интеграла в единичном $p$-мерном кубе V. Пусть $x = ({{x}_{1}},{{x}_{2}},...,{{x}_{p}})$ есть p-мерный вектор. Требуется найти

Точность сеточных методов стремительно падает с увеличением размерности p. Для получения приемлемой точности приходится брать все больше и больше точек, что делает расчеты непомерно трудоемкими и очень затратными по времени. В связи с этим при больших размерностях $\left( {p > 3} \right)$ используется метод Монте-Карло. Он предполагает использование случайных чисел, которые являются математической абстракцией. На практике же приходится использовать последовательности, лишь имитирующие случайные числа. От выбора такой последовательности сильно зависит работоспособность метода.

Расчеты представительных тестовых интегралов показывают, что для получения хорошей точности важна не столько случайность, сколько равномерность распределения точек. Наиболее эффективными оказываются последовательности Соболя с так называемыми “магическими” числами точек $N = {{2}^{n}},$ $n = 0,1,....$

В данной работе получены следующие результаты. Во-первых, предложены смещенные точки Соболя – модификация, улучшающая равномерность распределения точек и повышающая точность кубатур. Во-вторых, построена многосеточная стратегия, дающая апостериорную оценку точности. Преимущества предлагаемых алгоритмов проиллюстрированы на представительных тестовых примерах.

ПСЕВДОСЛУЧАЙНЫЕ ТОЧКИ

Метод Монте-Карло основан на том, что в кубе $V$ выбирают $N$ случайных точек ${{x}_{j}};$ при этом число $N$ может быть произвольным, в отличие от кубатурных формул на регулярных сетках. Кубатурная формула имеет схожий вид с формулой средних. Однако оценка ее погрешности оказывается кардинально иной.

Здесь $Df$ есть дисперсия. Оценка погрешности имеет не мажорантный, а вероятностный характер: величина погрешности распределена по закону Гаусса с указанным в формуле стандартом. Напомним, что погрешность не превышает 1 стандарта с вероятностью 0.68.

Оценка погрешности (2) не зависит от размерности p. Случайные точки сильно проигрывают регулярным сеткам при $p = 1$ или $p = 2.$ Уже при $p = 4$ зависимость погрешности от $N$ для случайных точек и регулярных сеток одинакова. При дальнейшем увеличении размерности случайные точки оказываются более выгодными; выигрыш быстро увеличивается при возрастании p.

Формулы (2) предполагают, что случайные точки ${{x}_{j}}$ имеют равномерную плотность распределения в кубе $V$ и не коррелированы. Однако строгих математических способов построения таких точек не найдено. Предложен ряд математических алгоритмов; получаемые при этом точки называют псевдослучайными. Построению псевдослучайных точек посвящена обширная литература, например, [1–13]. В отечественной и зарубежной литературе наиболее распространены следующие генераторы:

• вихрь Мерсенна (Mersenne twister) и быстрый вихрь Мерсенна (SIMD-oriented fast Mersenne twister);

• мультипликативный конгруэнтный генератор (Multiplicative congruential generator);

• мультипликативный генератор Фибоначчи с запаздыванием (64-bit multiplicative lagged Fibonacci generator),

• комбинированный множественный рекурсивный генератор (combined multiple recursive generator);

• генератор Philo4x32;

• генератор Threefry4x64;

• генератор Марсалья (Marsaglia’s SHR3 shift-register generator);

• модифицированный генератор Subtract-with-Borrow (modified Subtract-with-Borrow generator);

• модифицированная последовательность Лемера.

Именно эти генераторы реализованы во многих коммерческих пакетах (например, Matlab).

Качество каждой последовательности псевдослучайных чисел проверяют с помощью некоторых наборов тестов, основанных на теории вероятности [14–17]. Но никакой набор тестов не может быть полным и исчерпывающим. Поэтому такие проверки носят ограниченный характер. Даже простейшие визуальные тесты показывают, что широко распространенные последовательности не обеспечивают достаточно хорошей равномерности заполнения единичного квадрата [18, 19]. Вопрос о влиянии такой неравномерности на фактическую погрешность кубатур остается недостаточно ясным.

ТОЧКИ СОБОЛЯ

Последовательность Соболя определена неоднозначно. В ней использованы так называемые направляющие числа, вид которых может варьироваться. В ранних работах [1] таблицы направляющих чисел были построены для размерностей $p \leqslant 13$ и чисел $n \leqslant 20$ $\left( {N \leqslant {{2}^{{20}}}} \right).$ Позднее были построены числа для больших $p$ и $N$ [20]. Правда, при этом направляющие числа также менялись. В настоящее время доступна программа [21]. Вариант открытого доступа содержит $p \leqslant 50$ и $n \leqslant 31$ $\left( {N \approx 2 \cdot {{{10}}^{9}}} \right).$ Коммерческий вариант программы имеет $p \leqslant {{2}^{{16}}} - 1.$

Напомним, что последовательности Соболя отдельно строятся для каждого p. Нельзя из p‑мерной последовательности Соболя получить последовательность меньшего числа измерений. То же относится к магическим отрезкам последовательностей Соболя.

Сама кубатурная формула Соболя имеет тот же вид, что и (2). Но оценка ее погрешности не вполне ясна. Распределение точек лишь при магических $N$ приближается по свойствам к равномерному. При промежуточных $N$ оно получается выбрасыванием части точек и теряет свойство равномерности. Поэтому для кубатур следует использовать лишь магические N.

Предпринимались различные попытки обобщить последовательности Соболя. Однако поиски оптимальных вариантов таких обобщений неизменно приводили опять к последовательностям Соболя. Поэтому мы относимся к таким обобщениям осторожно.

СМЕЩЕНИЕ ТОЧЕК СОБОЛЯ

Расположение точек Соболя несколько асимметрично. Например, если взять $N = {{2}^{n}},$ то среднее арифметическое всех проекций точек на любую ось будет не 0.5, а $0.5\left( {1 - {1 \mathord{\left/ {\vphantom {1 N}} \right. \kern-0em} N}} \right).$ Очевидно, эта асимметричность не благоприятна для получения хорошей точности кубатур.

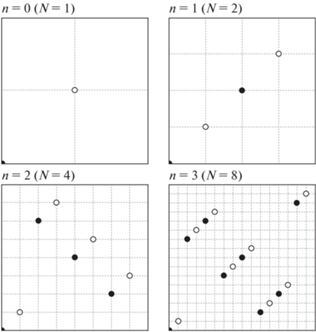
На рис. 1 черными кружками показаны двумерные точки Соболя для первых магических чисел. При $n = 0$ единственная точка лежит в углу единичного квадрата. Вычисление кубатуры по ней дает формулу первого порядка точности. Однако если сдвинуть эту точку на 0.5 по каждой координате, то кубатура по смещенной точке (светлый кружок) будет иметь второй порядок точности. Для случая $n = 1$ две точки расположены одна в углу квадрата и одна в центре, что также даст первый порядок точности. Но если сместить их на 0.25 по каждой координате, то погрешность кубатуры явно уменьшится. Поэтому можно предложить общий принцип смещения для любого числа измерений: если N = 2ⁿ, то прибавим ко всем координатам всех точек (2N)^–1. Это смещение целесообразно применять только для магических чисел Соболя. При этом смещения различны для различных N.

МНОГОСЕТОЧНЫЙ РАСЧЕТ

Тестовые расчеты показывают, что фактическая погрешность ${{\Delta }_{N}}$ убывает как $O\left( {{{N}^{{ - 1}}}} \right).$ Это наводит на мысль о возможности аппроксимации интеграла (и следовательно, его погрешности) как функции N. Однако эта аппроксимация не может быть гладкой, типа интерполяционной аппроксимации Ричардсона для сеточных методов. В данном случае точки получаются статистическими методами, поэтому их обработку нужно вести с помощью среднеквадратичной аппроксимации. Для этого нужно выбрать вид аппроксимации и приписать точкам какие-то веса.

В качестве рабочей гипотезы мы предположили закон убывания погрешности Δ_N ∼ N^–1. Но поскольку при увеличении $p$ явно проявляется статистический характер погрешности, то стандартное уклонение этих погрешностей мы приняли пропорциональными в степени ${{N}^{{ - 1{\text{/}}2}}}.$ Это и есть вес, используемый при аппркоксимации.

Была предложена следующая многосеточная процедура. Выполним расчет с магическими $N = {{2}^{n}},$ $n = 10,11,....$ В результате получим последовательность последовательность значений интеграла $\left\{ {{{I}_{N}}} \right\}.$ Теперь аппроксимируем эту последовательность по методу наименьших квадратов

Здесь a – уточненное значение интеграла. Одновременно вычислим стандартное уклонение ${{\sigma }_{a}}$ для величины a. Это стандартное уклонение является статистической оценкой точности для найденного значения интеграла.

Отметим, что начало последовательности $\left\{ {{{I}_{N}}} \right\},$ соответствующее $n = 0,1,...,9$ не учитывается при аппроксимации (3), поскольку эти сетки недостаточно подробны, и скорость убывания погрешности еще не соответствует $O\left( {{{N}^{{ - 1}}}} \right).$

ТЕСТОВЫЙ ИНТЕГРАЛ

Численные эксперименты целесообразно проводить на многомерных интегралах по единичному кубу, точные значения которых известны. Тогда можно непосредственно определять погрешность численного расчета и исследовать ее поведение. Обсудим, какие требования целесообразно предъявлять к подынтегральной функции.

В многомерных задачах используют понятие эффективной размерности функции. Например, рассмотрим две функции:

и где все ${{f}_{j}}({{x}_{j}})$ существенно отличны от констант. В первой функции все переменные в равной степени важны, и эффективная размерность функции равна p. Вторая функция зависит лишь от одной комбинации переменных, так что ее эффективная размерность равна 1. Чем больше эффективная размерность функции, тем задача труднее. Поэтому наиболее трудными оказываются функции первого типа.

Заметим, что не нарушая общности, можно считать все подынтегральные функции неотрицательными: их можно сделать неотрицательными путем прибавления константы, а такая процедура не влияет на погрешность любого метода. Пусть для функции типа произведения каждая ${{f}_{j}}$ существенно отлична от нуля лишь на участке длиной $\beta $ своего единичного ребра. Тогда произведение одномерных функций будет значимо отличаться от нуля в объеме ${{\beta }^{p}}.$ Если $\beta $ невелико, то при увеличении $p$ объем ${{\beta }^{p}}$ стремительно убывает; например, при $\beta = 0.1$ и $p = 10$ величина ${{\beta }^{p}} = {{10}^{{ - 10}}}.$ В этом случае для получения приемлемой точности любой метод Монте-Карло потребует числа узлов $N \gg {{\beta }^{{ - p}}}.$ Видно, что для того, чтобы число точек было разумным, следует брать $\beta $ близким к единице.

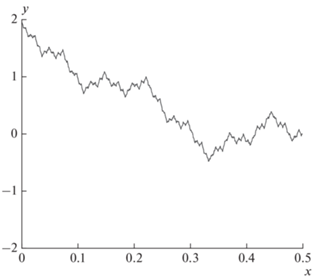
С учетом указанных соображений, в качестве теста мы выбрали тест вида (4). Он не является легким, несмотря на внешнюю простоту. Все ${{f}_{j}}$ будем считать одинаковыми и равными функции Вейерштрасса

где $a$ – произвольное нечетное число, не равное единице, а $b$ – положительное число, меньшее единицы. Известно, что при условиях $ab \geqslant 1,$ $a > 1$ функция Вейерштрасса непрерывна, но не имеет производной ни в одной точке. Такой тест исключительно сложен. Вид функции Вейерштрасса показан на рис. 2. С учетом симметрии функции Вейерштрасса интегрирование будем проводить по кубу со сторонами ${{x}_{j}} \in \left[ {0,0.5} \right].$ Для удобства отнормируем функцию Вейерштрасса так, чтобы выполнялось условие нормировки

РЕЗУЛЬТАТЫ РАСЧЕТОВ

Подсчитаем интеграл от многомерной функции Вейерштрасса (4), (6) с помощью трех качественно разных подходов: регулярной кубатуры на формулах трапеций, классического метода Монте-Карло с использованием Вихря Мерсенна и смещенных магических точек Соболя.

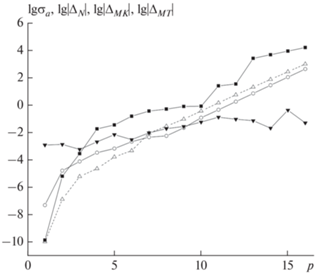
Сравним эти три подхода по величине погрешности при достаточно скромном числе точек $N = {{2}^{{20}}}.$ На рис. 3 приведены логарифмы погрешностей в зависимости от размерности p. Проанализируем приведенные кривые.

ЗАКЛЮЧЕНИЕ

Для вычисления многомерных интегралов наиболее эффективны магические точки Соболя. Предложено усовершенствование этих последовательностей – смещенные магические точки Соболя, обеспечивающие большую равномерность распределения точек в многомерном кубе. Это ощутимо повышает точность кубатур.

Существенной трудностью методов Монте-Карло является апостериорное подтверждение фактической точности. В данной работе предложен многосеточный алгоритм, позволяющий найти сеточное значение интеграла одновременно со статистически достоверной оценкой его точности. Ранее такие оценки были неизвестны.

Проведены расчеты представительных тестовых интегралов с высокой фактической размерностью $p$ (до $p = 16$). Рассматривались гладкие подынтегральные функции, а также многомерная функция Вейерштрасса, не имеющая производной ни в одной точке. Эти расчеты убедительно показывают преимущества предложенных методов.

Работа поддержана выполнена при поддержке Совета по грантам Президента РФ (проект № МК-3630.2021.1.1).