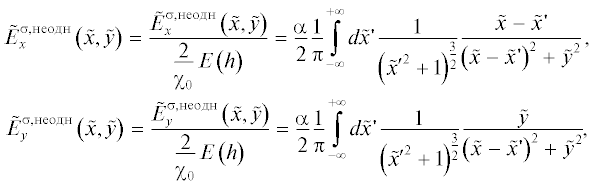Известия РАН. Серия физическая, 2022, T. 86, № 9, стр. 1251-1255

Электростатические поля поляризационных зарядов в диэлектрике с нелинейной восприимчивостью

М. Л. Акимов^1, *, М. А. Пятаков¹, О. П. Поляков¹, П. А. Поляков¹

¹ Федеральное государственное бюджетное образовательное учреждение высшего образования “Московский государственный университет имени М.В. Ломоносова”
Москва, Россия

^* E-mail: ml.akimov@physics.msu.ru

Поступила в редакцию 18.04.2022
После доработки 13.05.2022
Принята к публикации 23.05.2022

EDN: BKBFES
DOI: 10.31857/S0367676522090034

Полный текст (PDF)

Аннотация

Решена задача о вычислении электростатического поля, индуцированного нитью, заряженной с заданной линейной плотностью и расположенной над диэлектриком с конкретной нелинейной функциональной зависимостью диэлектрической восприимчивости от поля. Исследованы границы применимости метода изображений к расчету полей в поставленной задаче. Рассмотрены вклады наведенных объемных и поверхностных поляризационных зарядов в коллективное электрическое поле.

ВВЕДЕНИЕ

Известно решение классической электростатической задачи об электрическом поле, которое индуцировано в полубесконечном однородном диэлектрике с линейной поляризацией $\vec {P}$ зарядом с заданной линейной плотностью, когда тот находится над плоской поверхностью диэлектрика. В этом случае поляризация $\vec {P}$ пропорциональна напряженности электрического поля $\vec {E}$ в диэлектрической среде:

(1)

$\vec {P} = {{\varepsilon }_{0}}\chi \vec {E},$

где $\chi $ – диэлектрическая восприимчивость вещества, ${{\varepsilon }_{0}}$ – электрическая постоянная [1]. Поле при этом можно рассматривать, как поле пары фиктивных линейных зарядов, которые симметричны относительно плоской поверхности диэлектрика и называются электростатическими изображениями [1]. Причем можно провести аналогию с магнитными системами (удобство зависит от конкретной задачи), в этом случае вместо вектора поляризации будет рассматриваться вектор намагниченности, а вместо электрического поля – магнитное [2]. Если диэлектрик обладает диэлектрической восприимчивостью, которая не является постоянной величиной, а зависит от внешнего поля, в том числе нелинейно, то возможность применения метода электростатических изображений необходимо теоретически исследовать, так как метод может быть несправедлив. Но тогда для решения задачи потребуется рассмотрение нелинейных электростатических уравнений.

Подобные задачи имеют практическое применение, так как диэлектрики обладают рядом уникальных свойств по сравнению с другими веществами [3, 4]. Разрабатываются вычислительные методы для выявления новых свойств диэлектриков, изучаются новые композитные материалы и наноматериалы на основе и с применением изоляторов [5–7].

Широкое использование в технике нашли жидкие диэлектрики, которые применяются, например, в трибоэлектрических наногенераторах [8]. Они используются при изучении электрических разрядов в качестве среды, что в свою очередь важно для исследования новых и улучшения существующих способов получения водорода, наноматериалов и алмазов [9].

ПОСТАНОВКА ЗАДАЧИ

В работе рассматривается полубесконечная диэлектрическая среда с нелинейной поляризацией и с плоской поверхностью. Для этой нелинейной поляризации можно записать:

(2)

$\vec {P} = {{\varepsilon }_{0}}\chi \left( {\left| {\vec {E}} \right|} \right)\vec {E},$

а диэлектрическая восприимчивость задается в виде

(3)

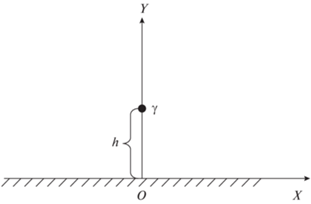
$\begin{gathered} \chi = \chi \left( {\left| {\vec {E}\left( {x,y} \right)} \right|} \right) = \frac{{{{P}_{s}}}}{{{{\varepsilon }_{0}}E}}\left( {1 - {{e}^{{{{ - E} \mathord{\left/ {\vphantom {{ - E} {{{E}_{k}}}}} \right. \kern-0em} {{{E}_{k}}}}}}}} \right) = \\ = \frac{{{{P}_{s}}}}{{{{\varepsilon }_{0}}{{E}_{k}}}}\frac{{{{E}_{k}}}}{E}\left( {1 - {{e}^{{{{ - E} \mathord{\left/ {\vphantom {{ - E} {{{E}_{k}}}}} \right. \kern-0em} {{{E}_{k}}}}}}}} \right) = {{\chi }_{0}}\frac{{{{E}_{k}}}}{E}\left( {1 - {{e}^{{{{ - E} \mathord{\left/ {\vphantom {{ - E} {{{E}_{k}}}}} \right. \kern-0em} {{{E}_{k}}}}}}}} \right), \\ \end{gathered} $

где ${{\chi }_{0}} = \frac{{{{P}_{s}}}}{{{{\varepsilon }_{0}}{{E}_{k}}}},$ ${{\chi }_{0}}$ – это начальная (постоянная) диэлектрическая восприимчивость, или восприимчивость при малых полях.

На рис. 1 показана данная система: линейный заряд $\gamma $ находится в вакууме на высоте $h$ над диэлектриком, введена декартова система координат, а диэлектрическая среда занимает полупространство $y \leqslant 0.$ Расчет поля поляризационных зарядов данной среды, индуцированных линейным точечным зарядом, сводится к решению следующей системы сингулярных интегральных уравнений:

(4)

$\left\{ {\begin{array}{*{20}{c}} {{{E}_{x}}\left( {x,y} \right) = {{E}_{{\gamma x}}}\left( {x,y} \right) + {{E}_{{\sigma x}}}\left( {x,y} \right) + {{E}_{{\rho x}}}\left( {x,y} \right),} \\ {{{E}_{y}}\left( {x,y} \right) = {{E}_{{\gamma y}}}\left( {x,y} \right) + {{E}_{{\sigma y}}}\left( {x,y} \right) + {{E}_{{\rho y}}}\left( {x,y} \right),} \end{array}} \right.$

где ${{E}_{{\gamma x}}}\left( {x,y} \right)$ и ${{E}_{{\gamma y}}}\left( {x,y} \right)$ – компоненты поля заряженной с линейной плотностью $\gamma $ нити, ${{E}_{{\sigma x}}}\left( {x,y} \right)$ и ${{E}_{{\sigma y}}}\left( {x,y} \right)$ – компоненты поля поверхностных индуцированных зарядов, ${{E}_{{\rho x}}}\left( {x,y} \right)$ и ${{E}_{{\rho y}}}\left( {x,y} \right)$ – компоненты поля объемных индуцированных зарядов. Данные компоненты определяются следующими соотношениями в любой точке с заданными координатами:

(5)

$\begin{gathered} {{E}_{{\gamma x}}}\left( {x,y} \right) = \frac{\gamma }{{2\pi {{\varepsilon }_{0}}}}\frac{x}{{{{x}^{2}} + {{{\left( {y - h} \right)}}^{2}}}},\,\,\,\,{{E}_{{\gamma y}}}\left( {x,y} \right) = \frac{\gamma }{{2\pi {{\varepsilon }_{0}}}}\frac{{y - h}}{{{{x}^{2}} + {{{\left( {y - h} \right)}}^{2}}}}, \\ {{E}_{{\sigma x}}}\left( {x,y} \right) = \frac{1}{{2\pi {{\varepsilon }_{0}}}}\int\limits_{ - \infty }^{ + \infty } {dx{\kern 1pt} '{{P}_{y}}\left( {x{\kern 1pt} ', - 0} \right)\frac{{x - x{\kern 1pt} '}}{{{{{\left( {x - x'} \right)}}^{2}} + {{y}^{2}}}}} , \\ {{E}_{{\sigma y}}}\left( {x,y} \right) = \frac{1}{{2\pi {{\varepsilon }_{0}}}}\int\limits_{ - \infty }^{ + \infty } {dx{\kern 1pt} '{{P}_{y}}\left( {x{\kern 1pt} ', - 0} \right)\frac{y}{{{{{\left( {x - x{\kern 1pt} '} \right)}}^{2}} + {{y}^{2}}}},} \\ {{E}_{{\rho x}}}\left( {x,y} \right) = - \frac{1}{{2\pi {{\varepsilon }_{0}}}}\int\limits_{ - \infty }^{ + \infty } {dx{\kern 1pt} '\int\limits_{ - \infty }^0 {dy{\kern 1pt} '} {\text{div}}\vec {P}\left( {x{\kern 1pt} ',y{\kern 1pt} '} \right)\frac{{x - x{\kern 1pt} '}}{{{{{\left( {x - x{\kern 1pt} '} \right)}}^{2}} + {{{\left( {y - y{\kern 1pt} '} \right)}}^{2}}}}} , \\ {{E}_{{\rho y}}}\left( {x,y} \right) = - \frac{1}{{2\pi {{\varepsilon }_{0}}}}\int\limits_{ - \infty }^{ + \infty } {dx{\kern 1pt} '\int\limits_{ - \infty }^0 {dy{\kern 1pt} '} {\text{div}}\vec {P}\left( {x{\kern 1pt} ',y{\kern 1pt} '} \right)\frac{{y - y{\kern 1pt} '}}{{{{{\left( {x - x{\kern 1pt} '} \right)}}^{2}} + {{{\left( {y - y{\kern 1pt} '} \right)}}^{2}}}}.} \\ \end{gathered} $

Рис. 1.

Линейный точечный заряд на высоте $h.$

Рассмотрим решение системы уравнений (4) и (5) методом последовательных приближений. Причем полагаем, что

(6)

$\frac{E}{{{{E}_{k}}}} \ll 1.$

Тогда выражение (3) приближенно будет равно

(7)

$\chi \approx {{\chi }_{0}}\left( {1 - \frac{E}{{2{{E}_{k}}}}} \right).$

Положим в первом приближении $\chi = {{\chi }_{0}}$ и найдем при $y > 0$

(8)

$\begin{gathered} {{E}_{{0x}}}\left( {x,y} \right) = \,\,\frac{\gamma }{{2\pi {{\varepsilon }_{0}}}}\frac{x}{{{{x}^{2}} + {{{\left( {y - h} \right)}}^{2}}}} - \frac{\gamma }{{2\pi {{\varepsilon }_{0}}}}\frac{{{{\chi }_{0}}}}{{2 + {{\chi }_{0}}}}\frac{x}{{{{x}^{2}} + {{{\left( {y + h} \right)}}^{2}}}}, \\ {{E}_{{0y}}}\left( {x,y} \right) = \,\,\frac{\gamma }{{2\pi {{\varepsilon }_{0}}}}\frac{{y - h}}{{{{x}^{2}} + {{{\left( {y - h} \right)}}^{2}}}} - \frac{\gamma }{{2\pi {{\varepsilon }_{0}}}}\frac{{{{\chi }_{0}}}}{{2 + {{\chi }_{0}}}}\frac{{y + h}}{{{{x}^{2}} + {{{\left( {y + h} \right)}}^{2}}}}, \\ \end{gathered} $

а при y ≤ 0

(9)

$\begin{gathered} {{E}_{{0x}}}\left( {x,y} \right) = \frac{\gamma }{{2\pi {{\varepsilon }_{0}}}}\frac{2}{{2 + {{\chi }_{0}}}}\frac{x}{{{{x}^{2}} + {{{\left( {y - h} \right)}}^{2}}}}, \\ {{E}_{{0y}}}\left( {x,y} \right) = \frac{\gamma }{{2\pi {{\varepsilon }_{0}}}}\frac{2}{{2 + {{\chi }_{0}}}}\frac{{y - h}}{{{{x}^{2}} + {{{\left( {y - h} \right)}}^{2}}}}. \\ \end{gathered} $

Отметим, что решения (8) и (9) согласуются с результатами, полученными методом изображений для однородных изотропных диэлектриков, у которых постоянная диэлектрическая восприимчивость [1, 10]. Положим в (8) и в (9), что ${{\chi }_{0}} \gg 1,$ и осуществим переход к безразмерным выражениям введением параметров $\tilde {x} = \frac{x}{h},$ $\tilde {y} = \frac{y}{h}.$ Получим из (8) и (9) соответственно

(10)

$\begin{gathered} {{{\tilde {E}}}_{{0x}}}\left( {\tilde {x},\tilde {y}} \right) = \frac{{{{E}_{{0x}}}\left( {\tilde {x},\tilde {y}} \right)}}{{\frac{2}{{{{\chi }_{0}}}}E\left( h \right)}} = \,\,\frac{{{{\chi }_{0}}}}{2}\frac{{\tilde {x}}}{{{{{\tilde {x}}}^{2}} + {{{\left( {\tilde {y} - 1} \right)}}^{2}}}} - \frac{{{{\chi }_{0}}}}{2}\frac{{\tilde {x}}}{{{{{\tilde {x}}}^{2}} + {{{\left( {\tilde {y} + 1} \right)}}^{2}}}}, \\ {{{\tilde {E}}}_{{0y}}}\left( {\tilde {x},\tilde {y}} \right) = \frac{{{{E}_{{0y}}}\left( {\tilde {x},\tilde {y}} \right)}}{{\frac{2}{{{{\chi }_{0}}}}E\left( h \right)}} = \,\,\frac{{{{\chi }_{0}}}}{2}\frac{{\tilde {y} - 1}}{{{{{\tilde {x}}}^{2}} + {{{\left( {\tilde {y} - 1} \right)}}^{2}}}} - \frac{{{{\chi }_{0}}}}{2}\frac{{\tilde {y} + 1}}{{{{{\tilde {x}}}^{2}} + {{{\left( {\tilde {y} + 1} \right)}}^{2}}}}, \\ \end{gathered} $

(11)

${{\tilde {E}}_{{0x}}}\left( {\tilde {x},\tilde {y}} \right) = \frac{{{{E}_{{0x}}}\left( {\tilde {x},\tilde {y}} \right)}}{{\frac{2}{{{{\chi }_{0}}}}E\left( h \right)}} = \frac{{\tilde {x}}}{{{{{\tilde {x}}}^{2}} + {{{\left( {\tilde {y} - 1} \right)}}^{2}}}},\,\,\,\,\,{{\tilde {E}}_{{0y}}}\left( {\tilde {x},\tilde {y}} \right) = \frac{{{{E}_{{0y}}}\left( {\tilde {x},\tilde {y}} \right)}}{{\frac{2}{{{{\chi }_{0}}}}E\left( h \right)}} = \frac{{\tilde {y} - 1}}{{{{{\tilde {x}}}^{2}} + {{{\left( {\tilde {y} - 1} \right)}}^{2}}}},$

где

(12)

$E\left( h \right) = \frac{\gamma }{{2\pi {{\varepsilon }_{0}}h}}.$

Используя метод последовательных приближений, подставляем (9) в (7), считая, что ${{\chi }_{0}} \gg 1,$ и переходим к безразмерным параметрам аналогично тому, как это было сделано в (10) и (11), получаем для диэлектрической восприимчивости

(13)

$\chi \approx {{\chi }_{0}}\left( {1 - \frac{\alpha }{2}\frac{1}{{\sqrt {{{{\tilde {x}}}^{2}} + {{{\left( {\tilde {y} - 1} \right)}}^{2}}} }}} \right),$

где

(14)

$\alpha = \frac{{2E\left( h \right)}}{{{{\chi }_{0}}{{E}_{k}}}}.$

Подставляем формулы (11) и (13) в ${{E}_{{\sigma x}}}\left( {x,y} \right),$ ${{E}_{{\sigma y}}}\left( {x,y} \right),$ ${{E}_{{\rho x}}}\left( {x,y} \right),$ ${{E}_{{\rho y}}}\left( {x,y} \right)$ из (5) (при условии ${{\chi }_{0}} \gg 1$), осуществляя переход к безразмерным выражениям введением параметров $\tilde {x} = \frac{x}{h},$ $\tilde {y} = \frac{y}{h},$ $\tilde {x}{\kern 1pt} ' = \frac{{x{\kern 1pt} '}}{h},$ $\tilde {y}{\kern 1pt} ' = \frac{{y{\kern 1pt} '}}{h},$ вычисляем поправочные к электрическому полю члены, которые обусловлены зависящей от этого поля восприимчивостью (7), а источниками этих дополнительных вкладов в суммарное электрическое поле являются поверхностные и объемные индуцированные заряды диэлектрической среды. Имеем

(15)

(16)

$\begin{gathered} {{{\tilde {E}}}_{{\rho x}}}\left( {\tilde {x},\tilde {y}} \right) = \frac{{{{E}_{{\rho x}}}\left( {\tilde {x},\tilde {y}} \right)}}{{\frac{2}{{{{\chi }_{0}}}}E\left( h \right)}} = - \frac{{{{\chi }_{0}}}}{{4\pi }}\int\limits_{ - \infty }^{ + \infty } {d\tilde {x}{\kern 1pt} '\int\limits_{ - \infty }^0 {d\tilde {y}{\kern 1pt} '\frac{\alpha }{{{{{\left( {{{{\tilde {x}}}^{{'2}}} + {{{\left( {y{\kern 1pt} ' - 1} \right)}}^{2}}} \right)}}^{{\frac{3}{2}}}}}}\frac{{\tilde {x} - \tilde {x}{\kern 1pt} '}}{{{{{\left( {\tilde {x} - \tilde {x}{\kern 1pt} '} \right)}}^{2}} + {{{\left( {\tilde {y} - \tilde {y}{\kern 1pt} '} \right)}}^{2}}}}} } , \\ {{{\tilde {E}}}_{{\rho y}}}\left( {\tilde {x},\tilde {y}} \right) = \frac{{{{E}_{{\rho y}}}\left( {\tilde {x},\tilde {y}} \right)}}{{\frac{2}{{{{\chi }_{0}}}}E\left( h \right)}} = - \frac{{{{\chi }_{0}}}}{{4\pi }}\int\limits_{ - \infty }^{ + \infty } {d\tilde {x}{\kern 1pt} '\int\limits_{ - \infty }^0 {d\tilde {y}{\kern 1pt} '\frac{\alpha }{{{{{\left( {{{{\tilde {x}}}^{{'2}}} + {{{\left( {\tilde {y}{\kern 1pt} ' - 1} \right)}}^{2}}} \right)}}^{{\frac{3}{2}}}}}}\frac{{\tilde {y} - \tilde {y}{\kern 1pt} '}}{{{{{\left( {\tilde {x} - \tilde {x}{\kern 1pt} '} \right)}}^{2}} + {{{\left( {\tilde {y} - \tilde {y}{\kern 1pt} '} \right)}}^{2}}}}} } , \\ \end{gathered} $

В (15) $\tilde {E}_{x}^{{\sigma ,{\text{неодн}}}}$ и $\tilde {E}_{y}^{{\sigma ,{\text{неодн}}}}$ – это часть компонент напряженности электрического поля, создаваемого поверхностными индуцированными зарядами диэлектрической среды, соответствующая неоднородной части диэлектрической восприимчивости – части восприимчивости, линейно зависящей от поля.

РЕЗУЛЬТАТЫ

Отметим, что из соотношений (15) и (16) видно, что зависящая от поля линейно (оставляются два слагаемых в разложении (7)) диэлектрическая восприимчивость (7) вносит поправку в суммарное поле пропорционально первой степени параметра $\alpha ,$ определяемого в (14).

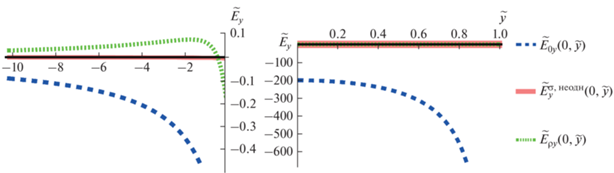
По формулам (10), (11), (15) и (16) построены зависимости при ${{\chi }_{0}} = 200 \gg 1,$ $\alpha = 0.01,$ то есть согласно (14) $\frac{{E\left( h \right)}}{{{{E}_{k}}}} = \frac{{\alpha {{\chi }_{0}}}}{2} = \frac{{0.01 \cdot 200}}{2} = 1.$ При построении были учтены особенности подынтегральных выражений в (15) и (16) (особые точки). Они заключаются в том, что в формулах (15) при $\tilde {x}{\kern 1pt} ' = \tilde {x},$ $\tilde {y} = 0$ и в формулах (16) при $\tilde {x}{\kern 1pt} ' = \tilde {x},$ $\tilde {y}{\kern 1pt} ' = \tilde {y}$ осуществляется деление нуля на ноль. Возникает сингулярность, которую необходимо устранить. Это было сделано путем разбиения области интегрирования и выкалывания особых точек. На рис. 2 слева показаны зависимости только для $y$-компонент поля, когда координаты $\tilde {x} = 0,$ а $ - 10 \leqslant \tilde {y} \leqslant - 0.01,$ справа – для $y$-компонент поля, когда $\tilde {x} = 0,$ а $0.01 \leqslant \tilde {y} \leqslant 0.99.$ График синего цвета – это $y$-компонента поля, вычисленного в первом приближении, то есть при постоянной диэлектрической восприимчивости; оранжевого – $y$-компонента поля поверхностных индуцированных зарядов; зеленого – $y$-компонента поля объемных индуцированных зарядов.

Рис. 2.

Графики полей: зависимость синего цвета – это $y$-компонента поля из первого приближения, оранжевого – $y$-компонента поля поверхностных индуцированных зарядов, зеленого – $y$-компонента поля объемных индуцированных зарядов.

ЗАКЛЮЧЕНИЕ

Из полученных зависимостей можем сделать вывод, что при данных значениях параметров объемные и поверхностные поляризационные заряды, обусловленные неоднородностью восприимчивости, если сравнивать модули, вносят незначительный вклад в коллективное электрическое поле. Это означает, что вплоть до значений $\frac{E}{{{{E}_{k}}}} = 1$ (в предельном случае $E = E\left( h \right)$ – максимально возможное поле), когда еще можно осуществлять разложение, как в (7), возможно с хорошей степенью точности пользоваться методом отображений, не ограничиваясь постоянством диэлектрической проницаемости. Это существенное утверждение, так как постоянство восприимчивости сильно ограничивало бы диапазон используемых полей.

Список литературы

Смайт В. Электростатика и электродинамика. М.: ИЛ, 1954. 604 с.
Пятаков М.А., Акимов М.Л., Поляков П.А. // Изв. РАН. Сер. физ. 2021. Т. 85. № 11. С. 1568; Piatakov M.A., Akimov M.L., Polyakov P.A. // Bull. Russ. Acad. Sci. Phys. 2021. V. 85. No. 11. P. 1230.
Wei T., Liu K., Fan P. et al. // Ceram. Int. 2021. V. 47. No. 3. P. 3713.
Shi J., Akbarzadeh A.H. // Compos. Struct. 2020. V. 250. Art. No. 112395.
Wang C.C., Pilania G., Boggs S.A. et al. // Polymer. 2014. V. 55. No. 4. P. 979.
Liu J., Zhang M., Guan L. et al. // Polymer Testing. 2021. V. 100. Art. No. 107236.
Chen L., Yan L., Guo Y. et al. // Synth. Met. 2020. V. 269. Art. No. 116555.
Wang J., Wu Z., Pan L. et al. // ACS Nano. 2019. V. 13. No. 2. P. 2587.
Лебедев Ю.А. // Физика плазмы 2017. Т. 43. № 6. С. 577; Lebedev Yu.A. // Plasma Phys. Rep. 2017. V. 43. No. 6. P. 685.
Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. М.: Наука, 1992. 664 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Серия физическая

Архивы выпусков Информация о журнале Отправить рукопись в журнал