Известия РАН. Серия физическая, 2023, T. 87, № 1, стр. 38-43

ВВЕДЕНИЕ

Графеновые сверхрешетки (ГСР), при получении которых используются различные способы формирования периодического потенциала, в последние годы широко исследуются теоретически и экспериментально. Непараболичность энергетического спектра ГСР позволяет ожидать проявления ряда нелинейных эффектов, известных для полупроводниковых сверхрешеток (СР). Одним из таких эффектов является распространение в сверхрешетках уединенных волн – солитонов и бризеров. В работе [1] было проанализировано уравнение Даламбера, записанное для электромагнитных волн, распространяющихся в ГСР, состоящей из чередующихся полосок щелевой и бесщелевой модификации графена [2]. Энергетический спектр сверхрешетки, рассмотренной в [1], имеет вид:

Здесь ${{p}_{x}},$ ${{p}_{z}}$ – компоненты квазиимпульса электрона, $d$ – период СР, ${{v}_{F}} = {{10}^{8}}\,\,см\, \cdot {{с}^{{ - 1}}}$ – скорость на поверхности Ферми в графене, $\Delta $ – полуширина запрещенной зоны в щелевой модификации графена. В расчетах будем полагать ${{\Delta }} = 0.13\,\,{\text{эВ,}}$ что соответствует полуширине запрещенной зоны графена на подложке из карбида кремния. Параметр ${{\Delta }_{1}}$ соответствует полуширине минизоны проводимости одномерной полупроводниковой СР. Например, в [3] полагают ${{{{\Delta }}}_{1}} = 0.059\,\,{\text{эВ}}{\text{.}}$ В настоящей работе будем считать значение ${{\Delta }_{1}}$ меньше или порядка $\Delta .$ Известно [1], что в этом материале вектор-потенциал электромагнитного поля является решением уравнения Даламбера, представляемого в виде

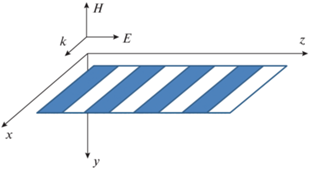
Здесь $\alpha = {{qd{{A}_{z}}} \mathord{\left/ {\vphantom {{qd{{A}_{z}}} {\hbar c}}} \right. \kern-0em} {\hbar c}}$ – безразмерная компонента векторного потенциала в направлении чередования слоев СР, $\omega _{0}^{2} = \frac{{2\pi {{n}_{0}}{{q}^{2}}{{d}^{2}}\Delta }}{{{{a}_{0}}{{\hbar }^{2}}}},$ ${{n}_{0}}$ – поверхностная концентрация носителей заряда, ${{a}_{0}} = 0.12$ – толщина графенового слоя, $b = {{{{\Delta }_{1}}} \mathord{\left/ {\vphantom {{{{\Delta }_{1}}} \Delta }} \right. \kern-0em} \Delta }.$ Уравнение колебаний в форме (2) соответствует направлению вектора напряженности электрического поля вдоль оси z, при этом волна распространяется вдоль оси х (рис. 1). Уравнение (2) имеет решение в виде $2\pi $-импульса, выраженное неявно [1]:

$\xi = \frac{{x - vt}}{{{{L}_{0}}}},$ ${{L}_{0}} = \frac{c}{{{{\omega }_{0}}}}\sqrt {1 - \frac{{{{v}^{2}}}}{{{{c}^{2}}}}} ,$ $v$ – скорость электромагнитного импульса. В работе [4] исследуется вопрос области стабильности $2\pi $-импульса в ГСР, а также динамика $\pi $-импульса. Исследованию взаимодействия кинков и антикинков уравнения (2) посвящен обзор [5]. В статье [6] численно исследовано неупругое столкновение кинков и антикинков с одинаковой, но противоположной по направлению скоростью. После взаимодействия кинка и антикинка они уходят в бесконечность, когда скорость рассматриваемых уединенных волн либо больше некоторого критического значения, либо находится внутри ряда резонансных окон; в противном случае они образуют состояние, подобное бризеру, которое медленно распадается за счет излучения энергии.

В работе [7] предложен способ получения приближенного решения нелинейного уравнения Клейна–Гордона в виде бегущего бризера малой амплитуды и в качестве примера исследовано решение уравнения (2), принимающее вид

$\gamma = {1 \mathord{\left/ {\vphantom {1 {\sqrt {{{1 - {{\vartheta }^{2}}} \mathord{\left/ {\vphantom {{1 - {{\vartheta }^{2}}} {{{c}^{2}}}}} \right. \kern-0em} {{{c}^{2}}}}} }}} \right. \kern-0em} {\sqrt {{{1 - {{\vartheta }^{2}}} \mathord{\left/ {\vphantom {{1 - {{\vartheta }^{2}}} {{{c}^{2}}}}} \right. \kern-0em} {{{c}^{2}}}}} }}.$ При выводе (4) предполагалось, что $\omega \approx 1$ и $\omega < 1.$

Наличие бризерного решения нелинейного уравнения интересно само по себе, а исследование динамики бризера в нелинейной среде может дать сведения о применимости ее, например, для передачи информации при помощи солитоноподобных импульсов [8]. Ряд исследований посвящен динамике уединенных волн, являющихся решениями уравнений типа Клейна–Гордона (см., например, [9–13], а также литературу, приведенную в [7]). В качестве экспериментального доказательства существования электромагнитного бризера в ГСР может выступить бризероэлектрический эффект, который должен проявляться в возникновении потока электронов в направлении распространения волны. В работе [14] рассмотрен эффект увлечения электронов в поле бризера в полупроводниковой СР в качестве примера использования бризерного решения уравнения синус-Гордона, описывающего распространение нелинейных волн в указанной структуре. Ряд работ (например, [15–17]) посвящены эффекту увлечения электронов солитонами (кинками) в полупроводниковых и графеновых сверхрешетках. В настоящей работе предпринята попытка решить аналогичную поставленной в [14] задачу о бризероэлектрическом эффекте в графеновой сверхрешетке.

ИССЛЕДОВАНИЕ БРИЗЕРОЭЛЕКТРИЧЕСКОГО ЭФФЕКТА В ГРАФЕНОВОЙ СВЕРХРЕШЕТКЕ В БЕССТОЛНОВИТЕЛЬНОМ ПРИБЛИЖЕНИИ

Геометрия задачи показана на рис. 1. Волна распространяется вдоль оси х (перпендикулярно к направлению чередования слоев сверхрешетки), вектор $\vec {E}$ электрической напряженности поля волны направлен вдоль оси z (вдоль оси сверхрешетки), вектор $\vec {H}$напряженности магнитного поля волны вдоль оси y, то есть $\vec {E} = \left\{ {0,0,E} \right\},$ $\vec {H} = \left\{ {0, - H,0} \right\}.$ Векторы $\vec {E}$ и $\vec {H}$ связаны с векторным потенциалом электромагнитного поля соотношениями

что в рассматриваемой геометрии задачи приводит к соотношениям

Учитывая, что значения величин $\omega $ и $\gamma $ близки к единице, выражение (4) для векторного потенциала бризера можно представить в виде произведения ${{A}_{z}} = PQ$ быстроосциллирующей функции $P$ и медленно меняющейся функции $Q{\text{:}}$

Дифференцируя только быстроосциллирующую часть, получаем соотношение между напряженностями электрического и магнитного полей:

В бесстолкновительном приближении плотность тока увлечения электронов бризером определяется следующим образом:

где $\overrightarrow u = \left\{ {{{u}_{x}},\,\,{{u}_{z}}} \right\}$ – вектор скорости электрона в ГСР, ${{p}_{x}},$ ${{p}_{z}}$ – решения классических уравнений движения электрона в поле электромагнитной волны

Ввиду малости ${{u}_{x}}$ по сравнению со скоростью света $c$ вторым слагаемым во втором уравнении системы (13) пренебрегаем. Воспользовавшись выражением (11), получаем:

Решая второе уравнение в (14), получаем

Поскольку рассматривается эффект увлечения электронов нелинейной волной, можно электрическое поле волны считать слабым в том смысле, что оно мало влияет на разогрев электронного газа в материале. Поэтому можно подобрать такие значения температуры, когда большинство электронов находятся вблизи дна минизоны проводимости и выполняется условие ${{p}_{0}}{{\nu }_{F}} \ll \Delta ,{{\Delta }_{1}},$ где ${{p}_{0}}$ – некоторое характерное значение абсолютной величины квазиимпульса электрона. В этом случае вторым слагаемым в знаменателе правой части первого уравнения в (14) можно пренебречь. Учитывая (15), первое из уравнений движения электрона принимает вид:

Интегрируя (16) в пределах от минус бесконечности до текущего момента времени $t,$ получаем:

Полагая, что в далеком прошлом векторный потенциал поля бризера был равен нулю, получаем

С учетом приближения ${{p}_{x}}{{\nu }_{F}} \ll \Delta ,{{\Delta }_{1}}$ выражение для плотности тока увлечения принимает вид:

Заряд, переносимый через единицу площади поперечного сечения образца (в рассматриваемом случае двумерной структуры – через единицу длины поперечного сечения), в результате прохождения бризера, определяется выражением

для определенности полагаем ${{x}_{0}} = 0.$ Преобразуем выражение (4). Введем новые переменные: Получаем:

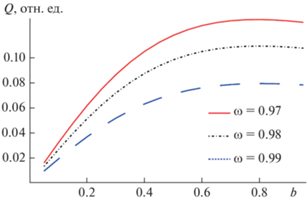
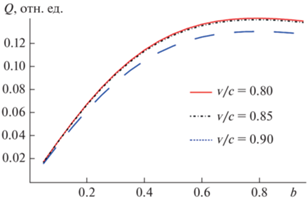
На рис. 2 и 3 приведены зависимости заряда, увлекаемого бризером, от параметра $b = {{{{\Delta }_{1}}} \mathord{\left/ {\vphantom {{{{\Delta }_{1}}} \Delta }} \right. \kern-0em} \Delta }$ при разных значениях параметров $\omega $ и ${v \mathord{\left/ {\vphantom {v c}} \right. \kern-0em} c},$ соответственно. Выбранные значения параметра $\omega $ и скорости $v$ обусловлены условиями существования решения в указанной форме. При характерных значениях параметров d = 2 ⋅ 10^–6 см, Δ = 0.13 эВ, n₀ = 10¹⁰ см^–2, υ_F = 10⁸ см/с, ${{a}_{0}}$ = 0.12 нм получаем величину увлеченного заряда, приходящуюся на единицу длины поперечного сечения, равной ${{Q}_{0}}$ = 5 ⋅ 10^–19 Кл/см. Полагая толщину образца порядка ${{a}_{0}},$ величина увлеченного бризером заряда, отнесенная к единице площади поперечного сечения, составляет примерно $Q_{0}^{'}$ = 10^–12 Кл/см², что по порядку величины совпадает со значением, полученным в работе [14] для полупроводниковой СР с одномерным периодическим потенциалом.

ВЫЧИСЛЕНИЕ ХАРАКТЕРНОГО ВРЕМЕНИ ПРОБЕГА БРИЗЕРА В ГРАФЕНОВОЙ СВЕРХРЕШЕТКЕ

Будем предполагать время свободного пробега электрона $\tau $ большим по сравнению со временем пребывания электрона в поле l/v (l – длина бризера), ${w \mathord{\left/ {\vphantom {w v}} \right. \kern-0em} v}$ ($w$ – ширина бризера, $v$ – скорость электрона). Тогда при определении формы бризера можно пренебречь столкновениями, а найденное таким образом поле волны подставить в уравнение Больцмана, учитывающее столкновения [14, 15]. При условии, что длина $\lambda $ свободного пробега электрона мала по сравнению с длиной $l$ бризера ($\lambda \ll l$), в уравнении Больцмана можно пренебречь членом с пространственной производной:

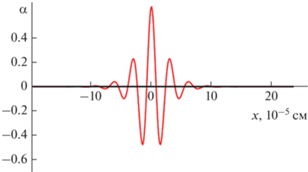
Средняя длина свободного пробега $\lambda $ в графене при комнатной температуре и концентрации носителей заряда $n\sim {{10}^{{12~}}}\,\,{\text{с}}{{{\text{м}}}^{{ - 2}}}$ составляет $\lambda \sim 4 \cdot {{10}^{{ - 5}}}\,\,{\text{см}}$ [18], при этом ширина бризера составляет порядка ${{10}^{{ - 4}}}\,\,~{\text{см}}$ (рис. 4), поэтому условие $\lambda \ll l$ выполняется в графеновой сверхрешетке значительно менее строго, чем в полупроводниковой [14–16].

В уравнении (25) $f\left( {{{p}_{x}},{{p}_{z}},t} \right)$ – функция распределения электронов проводимости, ${{f}_{0}}\left( {{{p}_{x}},{{p}_{z}}} \right)$ – равновесная функция распределения, поле бризера ${{E}_{z}}\left( {x,t} \right)$ определяется выражениями (7), (4). Решение уравнения (25) с начальным условием $f\left( {\vec {p},{{t}_{0}}} \right) = {{f}_{0}}\left( {\vec {p}} \right)$ имеет вид:

При стремлении t₀ к минус бесконечности первое слагаемое в (26) стремится к нулю. Выражение для электронной функции распределения принимает вид:

Равновесную функцию распределения возьмем в форме функции распределения Максвелла–Больцмана. Выражение для плотности тока вдоль направления колебаний электрического поля волны принимает вид:

В (28)–(30) был произведен переход к безразмерным переменным: ${{{{p}_{{x,z}}}d} \mathord{\left/ {\vphantom {{{{p}_{{x,z}}}d} \hbar }} \right. \kern-0em} \hbar } \to {{p}_{{x,z}}},$ ${{x{{\omega }_{0}}b} \mathord{\left/ {\vphantom {{x{{\omega }_{0}}b} c}} \right. \kern-0em} c} \to x,$ $t{{\omega }_{0}}b \to t,$ ${{kT} \mathord{\left/ {\vphantom {{kT} \Delta }} \right. \kern-0em} \Delta } \to T,$ и введены обозначения: ${{\beta }_{1}} = {{v_{F}^{2}{{\hbar }^{2}}} \mathord{\left/ {\vphantom {{v_{F}^{2}{{\hbar }^{2}}} {\left( {{{\Delta }^{2}}{{d}^{2}}} \right)}}} \right. \kern-0em} {\left( {{{\Delta }^{2}}{{d}^{2}}} \right)}},$ $\tau {\kern 1pt} ' = \tau {{\omega }_{0}}b,$ функция $\alpha \left( {x,t} \right)$ определяется выражением (22).

Для определения времени пробега бризера найдем скорость изменения его волнового импульса, отнесенную к единице площади поперечного сечения образца:

Импульс бризера (в расчете на единицу площади) равен

Из (31), (32) получаем время пробега бризера

Выражение (33) исследуется численно. Расчет показывает, что отношение интегралов в (33) дает величину порядка единицы. При характерных значениях параметров $b = {{{{\Delta }_{1}}} \mathord{\left/ {\vphantom {{{{\Delta }_{1}}} \Delta }} \right. \kern-0em} \Delta } = 0.25,$ $d = 2 \cdot {{10}^{{ - 6}}}$ см, Δ = 0.13 эВ, ${{n}_{0}}$ = 10¹⁰ см^–2, $\tau = {{10}^{{ - 10}}}$ c, $\varepsilon = 3.3,$ $T = 200$ К получаем величину ${{\tau }_{s}}\sim {{10}^{{ - 12}}}$ с. Для сравнения, в работе [14] в случае полупроводниковой сверхрешетки получили ${{\tau }_{s}} = {{10}^{{ - 10}}}$ с. Следует отметить, что используемое в настоящей работе бризерное решение является приближенным, форма которого сохраняется на протяжении около десяти ширин импульса, что соответствует приблизительно ${{10}^{{ - 12}}}{\text{--}}{{10}^{{ - 11}}}$ с. Поскольку вычисленное время пробега бризера, обусловленное влиянием столкновений, оказывается одного порядка с этой величиной, можно подобрать параметры сверхрешетки и внешнего поля, при которых бризероэлектрический эффект можно рассматривать в бесстолкновительном приближении.

ЗАКЛЮЧЕНИЕ

Таким образом, исследован бризероэлектрический эффект в графеновой сверхрешетке в бесстолкновительном приближении и оценено влияние столкновений электронов с неоднородностями кристаллической решетки на среднее время пробега бризера. В бесстолкновительном приближении величина увлеченного бризером заряда по порядку величины совпадает с зарядом, увлекаемым бризером в полупроводниковой сверхрешетке. За счет большей длины свободного пробега в графене по сравнению с типичными полупроводниками условие малости длины свободного пробега по сравнению с шириной бризера, требуемое для рассмотрения поля бризера как однородного, выполняется хуже, чем для полупроводниковой СР. За счет особенностей энергетического спектра ГСР интегралы в выражении для среднего времени пробега бризера приходится брать численно. Кроме того, исходя из способа получения выражения для времени пробега бризера эта величина, вообще говоря, зависит от времени, поэтому приведенные оценки среднего времени пробега бризера верны с точностью до порядка. Полученное время пробега бризера оказывается одного порядка со временем, в течение которого форма бризерного решения может считаться постоянной, что может служить обоснованием использования бесстолновительного приближения при расчете величины увлеченного заряда.