Известия РАН. Серия физическая, 2023, T. 87, № 1, стр. 44-48
Флоке-спектр дираковского кристалла в поле импульсного излучения
С. В. Крючков 1, 2, Е. И. Кухарь 2, *, Д. А. Силиванов 2
1 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Волгоградский государственный социально-педагогический университет”
Волгоград, Россия
2 Федеральное государственное бюджетное образовательное учреждение высшего образования
“Волгоградский государственный технический университет”
Волгоград, Россия
* E-mail: eikuhar@yandex.ru
Поступила в редакцию 29.08.2022
После доработки 16.09.2022
Принята к публикации 26.09.2022
- EDN: JIWCBE
- DOI: 10.31857/S0367676522700089
Аннотация
Вычислен флоке-спектр дираковского кристалла, помещенного в поле электромагнитного излучения, равного суперпозиции двух волн, поляризованных во взаимно перпендикулярных направлениях. Каждая из волн представляет собой последовательность импульсов гауссовского профиля. Исследована зависимость квазиэнергетической щели от коэффициента заполнения сигналов и временного сдвига между сигналами.
ВЕДЕНИЕ
Современные технологии позволяют получать низкоразмерные структуры различного типа, в том числе 2D кристаллы моноатомной толщины [1, 2]. Открытие так называемых дираковских и вейлевских кристаллов имеет не только практическое [3, 4], но и фундаментальное значение. Хорошо известно, что свободный графен характеризуется линейной зависимостью между энергией и импульсом электрона, т.е. коническим типом закона дисперсии. В то время как графену на подложке может соответствовать гиперболический тип закона дисперсии. Как видно имеет место математическое сходство электронных состояний в физике низкоразмерных систем и релятивистской квантовой физике. Последнее дает возможность использовать современные наноматериалы в качестве платформы для моделирования и проверки некоторых эффектов квантовой электродинамики [5–8]. Таким образом, изучение нелинейных оптических и электрических свойств дираковских и вейлевских кристаллов представляет интерес для той области, что развивающейся на стыке физики твердого тела и физики высоких энергий.
Уникальность указанных выше материалов объясняется наличием в квантовом уравнении для электронных состояний слагаемых, связывающих импульс носителя заряда с его псевдоспиновой степенью свободы. Следствием проявления такой связи являются, например, эффект Zitterbewegung [9–11], переходы типа “полуметалл – изолятор” [12–15] и “дираковский–полудираковский кристалл” [16, 17]. Благодаря которым реализуются так называемые флоке-топологические изоляторы [18]. На данный момент исследования взаимодействия дираковских материалов с ВЧ полем касаются в основном непрерывного режима ЭМ излучения. Ниже излагаются результаты исследования флоке-спектра дираковского кристалла, помещенного в поле импульсного излучения.
ФЛОКЕ-ФОРМАЛИЗМ И ФЛОКЕ-СПЕКТР
В отсутствие электромагнитного (ЭМ) излучения графен обладает полуметаллическим типом проводимости. Однако, если последний поместить в высокочастотное (ВЧ) поле ЭМ волны, то при определенных условиях возможен переход к состоянию зонного диэлектрика [12–15]. Здесь стоит отметить, что задача о взаимодействии кристалла с ВЧ излучением является нестационарной. Математической основой теории явлений, возникающих в квантовых системах, находящихся под управлением периодических полей, является флоке-формализм [13]. Подход к решению задач в рамках флоке-теории заключается в перенормировке гамильтониана системы, находящейся в периодическом поле, таким образом, чтобы проблема временной эволюции сводилась к стационарной задаче – задаче на собственные значения нового “эффективного” гамильтониана, не зависящего от времени. В этом случае говорят о флоке-спектре системы [15]. Таким образом, указанное выше диэлектрическое состояние носит характер динамически наведенного (усредненного по времени) состояния. Соответствующая перенормировка происходит с использованием унитарных операторов, включающих в себя быстро осциллирующие функции [19]. Такой подход успешно использовался для объяснения динамического сужения зон проводимости узкощелевых полупроводников [20], эффектов динамической локализации [21], фото-туннелирования [22], переходов между сверхтекучими и диэлектрическими фазами [23], возможности реализации искусственных флоке-топологических зонных изоляторов (ФТИ) [18], возможности управления осцилляциями Шубникова-де Гааза [19] и т.д. В [14] флоке-спектр трактуется как закон дисперсии для связанных электрон-фотонных состояний, возникающих в дираковских кристаллах, помещенных в сильное поле лазерного излучения.
Пусть дираковский кристалл связан с плоскостью xy, а ЭМ излучение распространяется вдоль оси Oz так, что электрическая составляющая осциллирует вдоль графеновой плоскости. В силу малости толщины моноатомного слоя можно воспользоваться дипольным приближением и считать, что электрическое поле в той области пространства, где расположен образец, не зависит от координат. Вместе с этим гамильтониан системы также не будет зависеть от координат [13]:
(1)
$H\left( {\vec {p},t} \right) = {{\upsilon }_{{\text{F}}}}\left( {\vec {p} + \frac{e}{c}\vec {A}} \right) \cdot \vec {\sigma }.$Здесь $\vec {\sigma } = \left( {{{\sigma }_{x}},{{\sigma }_{y}},{{\sigma }_{z}}} \right)$ – матрицы Паули, ${{\upsilon }_{{\text{F}}}}$ – скорость Ферми, $\vec {A}\left( {t + T} \right) = \vec {A}\left( t \right)$ – векторный потенциал ЭМ поля волны в плоскости xy, $T$ – период ЭМ излучения. Таким образом, задача о решении уравнения $i\hbar \dot {\psi } = H\left( t \right)\,\psi $ удовлетворяет требованиям теоремы Флоке, согласно которой спинор $\psi ,$ описывающий состояние электрона в 2D гексагональной структуре, можно записать в виде
(2)
$\psi \left( t \right) = {{e}^{{ - \frac{{i\tilde {\varepsilon }t}}{\hbar }}}}\chi \left( t \right),$(3)
$\left[ { - i\hbar \frac{\partial }{{\partial t}} + H} \right]\chi = \tilde {\varepsilon }\chi .$Решение нестационарной задачи (3) можно свести к решению однородной алгебраической системы уравнений [13]:
(4)
$\sum\limits_k {{{H}_{{n,k}}}{{u}_{k}}} = \left( {\tilde {\varepsilon } + n\hbar \Omega } \right){{u}_{n}}.$НАВЕДЕНИЕ ЗАПРЕЩЕННОЙ ЗОНЫ ИМПУЛЬСНЫМ ИЗЛУЧЕНИЕМ
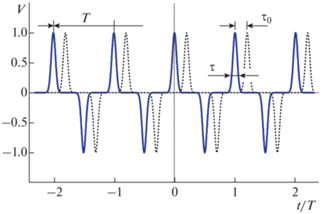
Считаем, что дираковский кристалл облучается двумя ЭМ волнами, поляризованными во взаимно перпендикулярных направлениях. Каждая из волн представляет собой последовательность импульсов гауссовского профиля. Длительность каждого импульса равна $\tau .$ Эти последовательности должны, кроме всего прочего, удовлетворять дополнительным требованиям. Во-первых, ни одна из них не должна иметь постоянных составляющих, т.е. усредненное по периоду $T$ значение напряженности электрического поля равно нулю ${{\left\langle {\vec {E}\left( t \right)} \right\rangle }_{T}} = 0.$ Во-вторых, они должны быть сдвинуты друг по отношению к другу на некоторое время ${{\tau }_{0}}$ (рис. 1). Согласно сказанному, напряженность электрического поля в плоскости xy равна
(5)
$\vec {E}\left( t \right) = {{E}_{0}}\left\{ {V\left( {t + {{\tau }_{0}}} \right),V\left( t \right)} \right\},$(6)
$V\left( t \right) = \sum\limits_{n = - \infty }^\infty {{{{\left( { - 1} \right)}}^{n}}F\left( {\frac{{2t - nT}}{{2\tau }}} \right)} ,\,\,\,\,F\left( \xi \right) = {{e}^{{ - {{\xi }^{2}}}}}.$Отношение ${\tau \mathord{\left/ {\vphantom {\tau T}} \right. \kern-0em} T}$ будем называть коэффициентом заполнения, полагая $\tau \ll T.$ Флоке-спектр носителей заряда в кристалле будем искать путем усреднения уравнения (3) по периоду сигналов. Для этого разложим периодическую функцию (6) в ряд Фурье (с учетом условия $\tau \ll T$):
(7)
$\begin{gathered} V\left( t \right) = \sum\limits_{k = - \infty }^\infty {{{C}_{{2k + 1}}}\left( {\Omega \tau } \right){{e}^{{i\left( {2k + 1} \right)\Omega t}}}} , \\ {{C}_{k}}\left( x \right) = \frac{x}{{\sqrt \pi }}\exp \left( { - \frac{{{{k}^{2}}{{x}^{2}}}}{4}} \right), \\ \end{gathered} $(8)
$\vec {A}\left( t \right) = \frac{{ic{{E}_{0}}}}{\Omega }\sum\limits_{k = - \infty }^\infty {\frac{{{{C}_{{2k + 1}}}\left( {\Omega \tau } \right)}}{{2k + 1}}{{e}^{{i\left( {2k + 1} \right)\Omega t}}}\left\{ {{{e}^{{i\left( {2k + 1} \right)\Omega {{\tau }_{0}}}}},1} \right\}} .$После подстановки (8) в выражение для величины ${{H}_{{n,k}}},$ фигурирующей в (4), запишем
(9)
$\begin{gathered} {{\upsilon }_{F}}\vec {p} \cdot \vec {\sigma }{{u}_{n}} + \hbar {{\Omega }_{0}} \times \\ \times \,\,\sum\limits_{k = - \infty }^\infty {\frac{{{{C}_{{2k + 1}}}}}{{2k + 1}}\left( {{{{\left( { - 1} \right)}}^{{k + 1}}}{{\sigma }_{x}} + i{{\sigma }_{y}}} \right){{u}_{{n + 2k + 1}}}} = \\ = \left( {\tilde {\varepsilon } + n\hbar \Omega } \right){{u}_{n}}, \\ \end{gathered} $(11)
${{\Delta }_{{\text{g}}}} = \frac{{8\hbar \Omega _{0}^{2}}}{\Omega }\left( {C_{1}^{2} - \frac{{C_{3}^{2}}}{{27}} + \ldots } \right).$Результат (11) получен с точностью до слагаемых, содержащих ${{C}_{n}}$ с $n \leqslant 3,$ однако он всегда может быть уточнен с повышением порядка спиноров ${{u}_{n}},$ удерживаемых в уравнениях (9).
К результату (11) можно прийти, если применить метод усреднения по быстрым осцилляциям [17]. Данный подход обладает большей наглядностью вычислений и позволяет относительно просто получить флоке-спектр вблизи дираковской точки. Согласно ему спинор $\chi \left( t \right),$ фигурирующий в (2), представляется в виде постоянной и ВЧ частей: $\chi \left( t \right) = {{u}_{0}} + {{u}_{{{\text{ac}}}}}\left( t \right),$ ${{u}_{0}} = {\text{const,}}$ $\left\langle {{{u}_{{{\text{ac}}}}}} \right\rangle = 0,$ причем $\left| {{{u}_{{{\text{ac}}}}}} \right| \ll \left| {{{u}_{0}}} \right|.$ После усреднения (3) по периоду ВЧ поля, запишем
(12)
${{\upsilon }_{{\text{F}}}}\vec {p} \cdot \vec {\sigma }\,{{u}_{0}} + \frac{{{{\upsilon }_{{\text{F}}}}e}}{c}\left\langle {\vec {A} \cdot \vec {\sigma }\,{{u}_{{{\text{ac}}}}}} \right\rangle = \,\tilde {\varepsilon }{{u}_{0}}$.Спинор uac можно найти, если в (3) оставить только ВЧ компоненты и отбросить все слагаемые, содержащие в качестве множителя ${{u}_{{{\text{ac}}}}}.$ Последнее оказывается возможным в силу условия (10). В результате получим
(13)
$\begin{gathered} {{u}_{{{\text{ac}}}}} = - \frac{{i{{\Omega }_{0}}}}{\Omega } \times \\ \times \,\,\sum\limits_{n = - \infty }^\infty {\frac{{{{C}_{{2n + 1}}}\left( {\Omega \tau } \right)}}{{{{{\left( {2n + 1} \right)}}^{2}}}}} {{e}^{{i\left( {2n + 1} \right)\Omega t}}}\left( {{{e}^{{i\left( {2n + 1} \right)\Omega {{\tau }_{0}}}}}{{\sigma }_{x}} + {{\sigma }_{y}}} \right){{u}_{0}}. \\ \end{gathered} $После подстановки (13) в (12) приходим к задаче на собственные значения
(14)
$\left( {{{\upsilon }_{{\text{F}}}}\vec {p} \cdot \vec {\sigma } + {{\Delta }_{{{\text{ac}}}}}{{\sigma }_{z}}} \right){{u}_{0}} = \tilde {\varepsilon }{{u}_{0}},$(15)
${{\Delta }_{{{\text{ac}}}}} = - {{\Delta }_{0}}\sum\limits_{n = 0}^\infty {\frac{{C_{{2n + 1}}^{2}\left( {\Omega \tau } \right)\sin \left( {2n + 1} \right)\Omega {{\tau }_{0}}}}{{{{{\left( {2n + 1} \right)}}^{3}}}}} ,$(16)
$\tilde {\varepsilon }\left( {\vec {p}} \right) = \pm \sqrt {\upsilon _{{\text{F}}}^{2}{{p}^{2}} + \Delta _{{{\text{ac}}}}^{2}} ,$Таким образом, если выполняется неравенство (10) квазиэнергетическая щель пропорциональна квадрату амплитуды, также, как и в случае эллиптически поляризованного гармонического сигнала [13, 14]. Из формул (15) и (17) также следует, что величина ${{\Delta }_{g}}$ определяется временным сдвигом импульсов ${{\tau }_{0}}.$ Например, если ${{\tau }_{0}} = 0,$ то щель не наводится. Если в (15) положить $\Omega {{\tau }_{0}} = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ и пренебречь слагаемыми с $n \geqslant 2,$ то результат (17) перейдет в (11). Графики зависимости квазиэнергетической щели от коэффициента заполнения сигналов и временного сдвига между сигналами, построенный по формулам (15) и (17), показан на рис. 2 и 3 соответственно. Из рис. 2 видно, что в рамках условия $\tau \ll T$ квазиэнергетическая щель увеличивается с ростом коэффициента заполнения. С помощью (15) можно показать, что квазиэнергетическая щель не наводится, если сдвиг во времени между последовательностями импульсов ${{\tau }_{0}}$ удовлетворяет условию: $2{{\tau }_{0}} = nT$ (n – целое число).
Рис. 2.
Зависимость квазиэнергетической щели от коэффициента заполнения сигналов (T = 0.16 пс): τ0 = = 39 (1), 16 (2) и 8 фс (3).
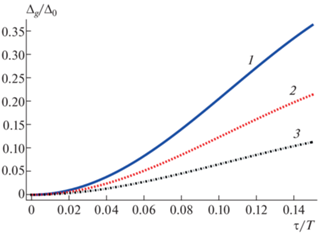
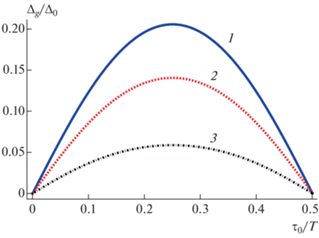
Рис. 3.
Зависимость квазиэнергетической щели от временного сдвига между сигналами (T = 0.16 пс): τ = = 16 (1), 12 (2) и 8 фс (3).
Отметим, что эффект динамического наведения запрещенной зоны ожидается и в том случае, если образец подвергнуть излучению, представляющему собой монополярную последовательность ЭМ импульсов: $E = {{E}_{0}}\left| {V\left( t \right)} \right|.$ Однако в этой ситуации у переменного электрического поля будет существовать постоянная составляющая, наличие которой не предполагается в применяемых выше методах вычислений. Тем не менее постоянную составляющую поля всегда можно убрать, создав в образце напряжение смещения, равное ${{E}_{{bias}}} = {{\sqrt \pi \tau {{E}_{0}}} \mathord{\left/ {\vphantom {{\sqrt \pi \tau {{E}_{0}}} T}} \right. \kern-0em} T}.$
ЗАКЛЮЧЕНИЕ
Выше вычислен флоке-спектр дираковского электрона в поле ЭМ волн, поляризованных во взаимно перпендикулярных направлениях. Режим излучения предполагался импульсным, а профиль отдельного ЭМ импульса – гауссовским. Результатом действия импульсного излучения также, как и в случае непрерывного синусоидального излучения [13, 14] является динамическое наведение запрещенной зоны в дираковской точке. Ширина ${{\Delta }_{g}}$ этой зоны растет с увеличением коэффициента заполнения сигналов (рис. 2). Одним из необходимых условий появления квазиэнергетической щели является наличие определенного сдвига во времени между последовательностями ЭМ импульсов, поляризованных во взаимно перпендикулярных направлениях. Таким образом, запрещенная зона не наводится ЭМ излучением, если сдвиг во времени ${{\tau }_{0}}$ удовлетворяет условию: $2{{\tau }_{0}} = nT$ (n – целое число), в частности, если ${{\tau }_{0}} = 0.$
Ширина запрещенной зоны ${{\Delta }_{g}}$ вычислена двумя способами: методом флоке-матрицы [13] и методом усреднения по быстрым осцилляциям [17]. Каждый из этих методов имеет свои преимущества. Первый позволяет для ширины ${{\Delta }_{g}}$ аналитически вычислить поправку любого порядка при произвольных значениях квазиимпульса электрона и амплитуды ЭМ поля, но требует длительных расчетов и для больших индексов у спиноров un – привлечения численных схем, реализуемых с помощью ЭВМ. Второй позволяет относительно просто вычислить флоке-спектр $\tilde {\varepsilon }\left( {\vec {p}} \right)$ и найти выражение для общего слагаемого ряда (15). Однако результат, полученный на его основе, справедлив при выполнении условия (10) и может быть отнесен только к окрестности дираковской точки.
В заключении оценим величину $\Omega ,$ удовлетворяющую неравенству (10). Положив здесь ${{\upsilon }_{F}}$ = = 108 см ⋅ с–1 и типичное для амплитуды напряженности электрического поля значение ${{E}_{0}}$ = = 102 В ⋅ см–1, найдем что для выполнения условия (10) достаточно использовать $\Omega $ ∼ 20–60 ТГц.
Список литературы
Khandelwal A., Mani K., Karigerasi M.H. et al. // Mater. Sci. Engin. B. 2017. V. 221. P. 17.
Zhang L., Hasan M.M., Tang Y. et al. // Mater. Today. 2021. V. 50. P. 442.
Prasongkit J., Shukla V., Grigoriev A. et al. // Appl. Surf. Sci. 2019. V. 497. Art. No. 143660.
Datta B., Vaidya J., Ghatak S. et al. // Appl. Phys. Lett. 2021. V. 119. Art. No. 133501.
Katsnelson M.I., Novoselov K.S., Geim A.K. // Nature Phys. 2006. V. 2. P. 620.
Katsnelson M.I. // Eur. Phys. J. B. 2006. V. 51. P. 157.
Young A.F., Kim P. // Nature Phys. 2009. V. 5. P. 222.
Фирсова Н.Е., Ктиторов С.А. // ФТТ. 2021. Т. 63. № 2. С. 277; Firsova N.E., Ktitorov S.A. // Phys. Solid State. 2021. V. 63. P. 313.
Cserti J., Dávid G. // Phys. Rev. B. 2006. V. 74. Art. No. 172305.
Rusin T.M., Zawadzki W. // Phys. Rev. B. 2013. V. 88. Art. No. 235404.
Белоненко М.Б., Янушкина Н.Н. // ФТТ. 2012. Т. 54. С. 2331; Belonenko M.B., Yanyushkina N.N. // Phys. Solid State. 2012. V. 54. P. 2462.
Delplace P., Gomez-Leon A., Platero G. // Phys. Rev. B. 2013. V. 88. Art. No. 245422.
Oka T., Aoki H. // Phys. Rev. B. 2009. V. 79. Art. No. 081406.
Kibis O.V. // Phys. Rev. B. 2010. V. 81. Art. No. 165433.
Weber C.P. // J. Appl. Phys. 2021. V. 129. Art. No. 070901.
Montambaux G., Piéchon F., Fuchs J.-N. et al. // Eur. Phys. J. B. 2009. V. 72. P. 509.
Kukhar E.I., Kryuchkov S.V. // Physica E. 2021. V. 134. Art. No. 114811.
Wang Y.H., Steinberg H., Jarillo-Herreroand P. et al. // Science. 2013. V. 342. P. 453.
Kibis O.V., Morina S., Dini K. et al. // Phys. Rev. B. 2016. V. 93. Art. No. 115420.
Holthaus M. // Phys. Rev. Lett. 1992. V. 69. P. 351.
Creffield C.E., Sols F., Ciampini D. et al. // Phys. Rev. A. 2010. V. 82. Art. No. 035601.
Ma R., Tai M.E., Preiss P.M. et al. // Phys. Rev. Lett. 2011. V. 107. Art. No. 095301.
Eckardt A., Weiss C., Holthaus M. // Phys. Rev. Lett. 2005. V. 95. Art. No. 260404.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Серия физическая