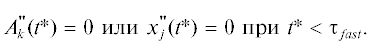1. На главную
  2. Электронные версии
  3. Химическая физика
  4. T. 39, № 9, 2020

Химическая физика, 2020, T. 39, № 9, стр. 23-30

Кинетические особенности быстрых релаксаций химических реакций

Н. И. Кольцов *

Чувашский государственный университет им. И.Н. Ульянова
Чебоксары, Россия

* E-mail: koltsovni@mail.ru

Поступила в редакцию 19.08.2019
После доработки 06.11.2019
Принята к публикации 20.11.2019

Полный текст (PDF)

Аннотация

В начале переходных процессов нелинейных химических реакций происходят быстрые изменения кинетических характеристик, которые зачастую не наблюдаются в ходе нестационарных экспериментов. Эти периоды быстрых релаксаций могут нести важную информацию о механизмах сложных реакций. В работе исследована эволюция периода быстрых релаксаций типовых химических реакций по мере удаления от равновесия. Введена трехуровневая классификация форм неравновесных кинетических зависимостей по уровню информативности. Максимальную информативность имеют немонотонные кривые с перегибами (“овраги” и “холмы”), среднюю − монотонные кривые с перегибами (“волны”), минимальную − монотонные кривые без перегибов (“спуски” и “подъемы”). Сформулирован критерий существования периода быстрых релаксаций, в течение которого существуют информативные формы кинетических кривых (овраги, холмы, волны). Показано, что при их исследовании могут наблюдаться состояния “ложного” равновесия, в которых кинетические кривые кажутся постоянными вдали от равновесия. Полученные результаты могут быть полезны при реконструкции механизмов химических реакций.

Ключевые слова: неравновесная кинетика, сложные реакции, быстрая релаксация.

ВВЕДЕНИЕ

Нестационарные кинетические модели нелинейных химических реакций, протекающих в реакторе идеального смешивания (РИС) , описываются системами обыкновенных дифференциальных уравнений (ОДУ), см., например, [1–9]. Решения таких ОДУ представляют собой зависимости концентраций реагентов от времени, кинетических параметров и начальных условий. Для различных реакций эти зависимости, вообще говоря, различны, т.е. являются своеобразными кинетическими портретами (кодами) [10–18]. Равновесные портреты различаются только формой зависимостей, которая может быть довольно сложной (гистерезисы, изломы, петли, изолы) [10–14]. Неравновесные портреты менее экзотичны, но могут включать любые специфические параметры кинетических кривых [15–27]. Так, в работе [15] доказано простое (но важное) свойство зависимости скорости линейных реакций (с конечным числом затухающих колебаний) от времени − число интервалов монотонности не может быть больше числа независимых реагентов. Если же число затухающих колебаний бесконечно (это возможно при двух и более независимых реагентах), то это свойство не выполняется и число интервалов монотонности может быть любым. На практике такое бесконечно затухающее колебание может выглядеть как конечно-затухающее и приводить к неверным выводам.

В работах [16–18] предложена классификация неравновесных концентрационных кривых на основе трех признаков, описывающих их форму, − специальных точек, пересечений и совпадений. На основе этой классификации для последовательной реакции выделено и проанализировано шесть типов (patterns) специальных точек (высшая, Эйлера, Ламберта, касания, золотая и тройная) и 6 из 612 возможных комбинаций взаимного расположения (reciprocal relations) кинетических кривых. Классификация характеристик длительности переходных процессов в зависимости от удаленности от равновесия (линейные и нелинейные времена релаксации, медленные релаксации, бесконечные релаксации) и их связь с равновесными характеристиками подробно исследованы в работах [6, 19–27] и др. Для экспериментального исследования химических реакций применяются различные релаксационные методы, см., например, [28–32]. Современные нестационарные методы TAP, SSITKA и другие обеспечивают временны́е разрешения не выше ∼10–3–10–5 с. Поэтому элементарные поверхностные процессы с малыми характерными временами остаются малоизученными [29]. Эти работы показывают, что изучение свойств неравновесных нелинейных кинетических процессов остается актуальным.

Исследуем связи между переходными процессами, формой кинетических кривых и механизмами нелинейных химических реакций вдали от равновесия. Для этого введем классификацию неравновесных форм кинетических кривых по сложности: немонотонные с экстремумами, монотонные с перегибами и монотонные без перегибов, т.е. по особенностям скорости и ускорения. Время протекания реакции разделим на два релаксационных периода − вблизи равновесия (медленный) и вдали от равновесия (более быстрый). Медленные релаксации соответствуют линейному (квазилинейному) протеканию реакции и хорошо наблюдаются, но малоинформативны. Более быстрые релаксации отражают основные нелинейные свойства исследуемого процесса и часто наблюдаются хуже, но более информативны. Наблюдаемость быстрых релаксаций зависит от значений кинетических параметров, экспериментальных методов и оборудования. При определенных значениях кинетических параметров наиболее быстрые релаксационные процессы могут становиться невидимыми для наблюдателя. В результате чего информация о некоторых важных свойствах химической реакции может быть потеряна. Проанализируем подробнее период быстрых релаксаций и его информационную значимость для понимания истинной кинетики исследуемого процесса.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Пусть химическая реакция $\sum {{{a}_{{ik}}}{{{\text{A}}}_{k}}} $ = $\sum {{{a}_{{ - ik}}}{{{\text{A}}}_{k}}} $ с участием основных (наблюдаемых) веществ Ak, k = 1, …, N, и промежуточных (ненаблюдаемых) веществ Xj, j = 1, …, n, протекает через стадии:

(1)
$\begin{gathered} \sum {{{a}_{{ik}}}{{{\text{A}}}_{k}}} + \sum {{{b}_{{ij}}}{{{\text{X}}}_{j}}} = \sum {{{b}_{{ - ij}}}{{{\text{X}}}_{j}}} + \sum {{{a}_{{ - ik}}}{{A}_{k}}} , \\ i = 1, \ldots ,I, \\ \end{gathered} $
где a±ij ≥ 0, b±ik ≥ 0 – стехиометрические коэффициенты веществ в стадии i. Динамика этой реакции в безградиентном реакторе описывается ОДУ с начальными условиями (н.у.) Ak(0) = Ak0, xj(0) = xj0:
(2)
$A_{k}^{'} = \sum {({{a}_{{ - ik}}} - {{a}_{{ik}}})({{r}_{i}} - {{r}_{{ - i}}})} + {{q}^{0}}A{{_{k}^{0}}^{{}}}--q{{A}_{k}},$
(3)
$x_{j}^{'} = \sum {({{b}_{{ - ij}}} - {{b}_{{ij}}}){{{({{r}_{i}} - {{r}_{{ - i}}})}}_{j}}} ,$
где Ak и xj – концентрации основных и промежуточных веществ, мольн. доли; r±I = ${{k}_{{ \pm i}}}\Pi A_{k}^{{a \pm ik}}x_{j}^{{b \pm {\text{i}}k}}$ – скорости стадий в прямом и обратном направлениях, 1/с; k±i – константы скоростей стадий, 1/с; q0 и q – скорости потока на входе и выходе реактора, 1/с; $A_{k}^{0}$ – концентрации основных веществ на входе реактора (индекс “0” сверху обозначает данные на входе реактора, а индекс “0” снизу – н.у.).

В равновесии $A_{k}^{'}$ = 0, $x_{j}^{'}$ = 0 и система уравнений (2), (3) становится алгебраической:

(4)
$\begin{gathered} \sum {({{a}_{{ - ik}}} - {{a}_{{ik}}})({{r}_{i}} - {{r}_{{ - i}}})} = q{{A}_{k}} - {{q}^{0}}A_{k}^{0}, \\ \sum {({{b}_{{ - ij}}} - {{b}_{{ij}}}){{{({{r}_{i}} - {{r}_{{ - i}}})}}_{j}}} = 0. \\ \end{gathered} $

Если уравнения (4) нелинейны, то они допускают несколько физичных решений (равновесий)

(5)
$\begin{gathered} {{A}_{{k\infty }}} = {{A}_{{k\infty }}}\left( {{{k}_{{ \pm i}}},{{q}^{0}},q,A_{k}^{0}} \right), \\ {{x}_{{j\infty }}} = {{x}_{{j\infty }}}\left( {{{k}_{{ \pm i}}},{{q}^{0}},q,A_{k}^{0}} \right), \\ \end{gathered} $

координаты которых зависят от кинетических параметров реакции и в общем случае не могут быть записаны аналитически. Устойчивость равновесий (5) в линейном приближении определяется спектром собственных чисел λp = λp(k±i, q0, q), p = = 1, …, s, т.е. корнями характеристического уравнения, вычисленными в этих равновесиях [1]:

${{\lambda }^{s}} + {{\sigma }_{1}}{{\lambda }^{{s - 1}}} + \ldots + {{\sigma }_{s}} = 0,$

где σp − определители порядка p из частных производных от правых частей системы (2), (3). Если действительная часть характеристического корня

(6)
${\text{Re}}{{\lambda }_{p}} < 0,\,\,\,\,p = 1, \ldots ,s,$

то равновесие устойчиво, а иначе – неустойчиво. Если при условии (6) выполняется и равенство для мнимой части характеристического корня:

(7)
${\text{Im}}{{\lambda }_{p}} = 0,\,\,\,\,p = 1, \ldots ,s,$

то кинетические кривые допускают только конечное число затухающих колебаний [1–3, 15], которые вблизи равновесия исчезают полностью (топологический тип – узел). В противном случае, т.е., если условие (7) не выполняется, кинетические кривые допускают (теоретически) бесконечное число колебаний, которые не прекращаются и вблизи равновесия (топологический тип − фокус). Их специфику дополнительно описывают любые амплитудно-частотные характеристики (период, частота и др.).

Для удобства введем простую классификацию типов форм и релаксаций. Разделим неравновесные формы кинетических кривых на немонотонные с экстремумами (“овраги” и “холмы”), монотонные с перегибами (“волны” вниз или вверх) и монотонные без перегибов (“спуски” и “подъемы”). Разделим процесс движения к равновесиям на три релаксационных “периода” – начальный (самый быстрый), средний (более медленный) и конечный (медленный). Рассмотрим особенности этих периодов по мере удаления от равновесия.

Медленные релаксации. Переходные процессы вблизи устойчивых равновесий происходят медленно (квазилинейно), не зависят от н.у. и носят затухающий характер. Форма кинетических кривых на этом участке может быть только монотонной без перегибов (“спуски”, “подъемы”) или немонотонной с бесконечным числом колебаний малой амплитуды (“овражки” и “холмики”) [15–18]. Темп движения к устойчивому равновесию характеризует линейное время релаксации [19–25]. Это время не зависит от н.у., а зависит только от кинетических параметров реакции и является временнóй константой реакции, которая может быть как угодно большой (медленные релаксации):

(8)
$\tau \left( {{{k}_{{ \pm i}}},{{q}^{0}},q,A_{k}^{0}} \right) = {{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {{\text{min}}\left| {{\text{Re}}{{\lambda }_{p}}} \right|}}} \right. \kern-0em} {{\text{min}}\left| {{\text{Re}}{{\lambda }_{p}}} \right|}}.$

Средние релаксации. Вдали от равновесий переходные процессы в системе (2), (3) происходят быстрее и описываются решениями задачи Коши с заданными начальными условиями. Форма кинетических кривых на этом участке зависит от н.у., устойчивости и типов равновесий и может быть монотонной (“спуски”, “подъемы” и “волны”) или немонотонной с конечным или бесконечным числом колебаний большой амплитуды (“овраги” и “холмы”) [15–18]. Такие кривые можно характеризовать числом и частотой экстремумов, размахом, скоростью изменения и т.д. Особенности релаксации к равновесиям (в линейном приближении) определяются всем спектром собственных чисел, а длительность переходного процесса характеризуется нелинейным временем релаксации, за которое достигается малая окрестность равновесия [19, 26, 27]. Это время, как правило, обратно пропорционально кинетическим параметрам реакции и больше линейного времени релаксации

(9)
${{\tau }_{{a{v}}}}\left( {{{k}_{{ \pm i}}},{{q}^{0}},q,A_{k}^{0},{{A}_{{k0}}},{{x}_{{j0}}}} \right)\sim {{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} {{\text{min}}(q,{{k}_{{ \pm i}}})}}} \right. \kern-0em} {{\text{min}}(q,{{k}_{{ \pm i}}})}} > \tau .$

Быстрые релаксации. Выделим из периода средних релаксаций начальный этап (подпериод) вблизи н.у. реакции, т.е. максимально удаленный от равновесий. На этом этапе переходные процессы в системе (2), (3) зависят от тех же кинетических параметров и н.у., но специфические особенности этих процессов не всегда могут наблюдаться экспериментально (быстрые релаксации). Если эти параметры превысят некоторые критические значения: k±i > $k_{{ \pm i}}^{*},$ то этот период будет протекать очень быстро (практически мгновенно) и перестанет быть наблюдаемым в стандартных экспериментах:

(10)
${{\tau }_{{fast}}}\left( {{{k}_{{ \pm i}}},{{q}^{0}},q,A_{k}^{0},{{A}_{{k0}}},{{x}_{{j0}}}} \right)\sim {{t}_{{resp}}} \to 0,$

где tresp – время отклика, зависящее от параметров оборудования (разрешающей способности, погрешности измерений и других; далее полагаем tresp ∼ 10−3). Если в этом периоде, т.е. вдали от равновесия (вблизи н.у.), происходят качественные изменения формы какой-либо кинетической кривой (существуют экстремумы или перегибы), то обязательно изменяется ее выпуклость (ускорение проходит через ноль) и выполняется хотя бы одно из равенств [33]

(11)

Равенства (11) с учетом (2), (3) выражаются через концентрации реагентов явным образом (после дифференцирования константы ${{q}^{0}}A_{k}^{0}$ в правых частях исчезают) и могут быть записаны в виде

(12)
$\sum {({{a}_{{ - ik}}} - {{a}_{{ik}}})} (r_{i}^{'} - r_{{ - i}}^{'}) = qA_{k}^{'},\,\,\,\,{{A}_{k}} \to {{A}_{{k0}}},$
(13)
$\sum {({{b}_{{ - ij}}} - {{b}_{{ij}}})} (r_{i}^{'} - r_{{ - i}}^{'}) = 0,\,\,\,\,{{x}_{j}} \to {{x}_{{j0}}},$

где

$r_{{ \pm i}}^{'} = {{k}_{{ \pm i}}}\sum {\left( {{{a}_{{ \pm ik}}}A_{k}^{{a \pm ik - {\text{1}}}}A_{k}^{'}x_{j}^{{b \pm {\text{i}}k}} + {{b}_{{ \pm ik}}}A_{k}^{{a \pm ik}}x_{j}^{{b \pm {\text{i}}k - {\text{1}}}}x_{j}^{'}} \right)} .$

Каждое из этих соотношений связывает неравновесные концентрации реагентов и параметры механизма реакции.

Если соотношения (12), (13) выполняются хотя бы для одного реагента, то его концентрация изменяется во времени в виде конечного (для равновесий типа узел) или бесконечного (для равновесий типа фокус) числа интервалов монотонности, т.е. кинетические кривые могут иметь форму “оврагов”, “холмов” или “волн”. При этом концентрации реагентов, для которых эти соотношения не выполняются, всегда изменяются монотонно без перегибов в течение всего переходного процесса, т.е. кинетические кривые этих реагентов могут иметь только форму “спусков” или “подъемов”. В противном случае, если соотношения (12), (13) не выполняются ни для одного реагента, то движение к равновесию происходит только монотонно без перегибов для всех реагентов, т.е. в форме “спусков” или “подъемов”. Таким образом, соотношения (12), (13) выражают критерий существования периода быстрых релаксаций в реакции (1). Общий алгоритм применения этого критерия следующий: 1) задаем предполагаемый механизм реакции (1); 2) записываем ее динамическую модель (2), (3); 3) записываем закон сохранения (ЗС) на основе динамической модели; 4) записываем соотношения (12), (13) для динамической модели; 5) переписываем эти соотношения с учетом ЗС; 6) анализируем выполнимость полученных соотношений по каждому реагенту с учетом н.у.; 7) если н.у. выполнимы (непротиворечивы), то быстрые релаксации по данному реагенту возможны, иначе – невозможны. Отметим, что в конкретных реакциях соотношения (12), (13) позволяют получить дополнительную информацию о механизме процесса – например, возможность или невозможность одновременного наблюдения разных форм кинетических кривых и др. (см. ниже пример 3).

Рассмотрим особенности кинетики быстрых релаксаций на примерах нелинейных реакций. Для этого растянем масштаб времени вблизи н.у. с необходимой дискретностью, превышающей стандартное время отклика оборудования (замедленная “съемка”).

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Пример 1. Пусть реакция A = B протекает в закрытой системе по нелинейной циклической схеме

(1.1)
$2{\text{A}} = 2{\text{B,}}\,\,\,\,{\text{B}} = {\text{A}},$

где A и B – реагенты. Ее динамическая модель (2) имеет вид

(1.2)
$\begin{gathered} A{\kern 1pt} ' = - 2{{k}_{1}}{{A}^{2}} + 2{{k}_{{ - 1}}}{{B}^{2}} + {{k}_{2}}B - {{k}_{{ - 2}}}A, \\ B{\kern 1pt} ' = 2{{k}_{1}}{{A}^{2}} - 2{{k}_{{ - 1}}}{{B}^{2}} - {{k}_{2}}B + {{k}_{{ - 2}}}A. \\ \end{gathered} $

В этой реакции при начальных условиях A0 = 1, B0 = 0 выполняется ЗС A + B = A0 + B0 = 1, и в равновесии (4) уравнения (1.2) запишутся как 2k1A2 – – 2k−1(1 – A)2 – k2(1 – A) + k–2A = 0. Отсюда с учетом (5)–(7) следует наличие единственного (детального [10]) устойчивого равновесия типа “узел”:

(1.3)
${{A}_{\infty }} = {{\left\{ {{{{\left[ {{{{({{k}_{2}} + {{k}_{{ - 2}}})}}^{2}} + 8({{k}_{1}}{{k}_{2}} + 2{{k}_{1}}{{k}_{{ - 1}}} + {{k}_{{ - 1}}}{{k}_{{ - 2}}})} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} - {{k}_{2}} - {{k}_{{ - 2}}} - 4{{k}_{{ - 1}}}} \right\}} \mathord{\left/ {\vphantom {{\left\{ {{{{\left[ {{{{({{k}_{2}} + {{k}_{{ - 2}}})}}^{2}} + 8({{k}_{1}}{{k}_{2}} + 2{{k}_{1}}{{k}_{{ - 1}}} + {{k}_{{ - 1}}}{{k}_{{ - 2}}})} \right]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} - {{k}_{2}} - {{k}_{{ - 2}}} - 4{{k}_{{ - 1}}}} \right\}} {(4{{k}_{1}} - 4{{k}_{{ - 1}}})\,\,{\text{при}}\,\,{{k}_{1}} \ne {{k}_{{ - 1}}}}}} \right. \kern-0em} {(4{{k}_{1}} - 4{{k}_{{ - 1}}})\,\,{\text{при}}\,\,{{k}_{1}} \ne {{k}_{{ - 1}}}}}.$
(1.4)
${{A}_{\infty }} = {{(2{{k}_{1}} + {{k}_{2}})} \mathord{\left/ {\vphantom {{(2{{k}_{1}} + {{k}_{2}})} {(4{{k}_{1}} + {{k}_{2}} + {{k}_{{ - 2}}})}}} \right. \kern-0em} {(4{{k}_{1}} + {{k}_{2}} + {{k}_{{ - 2}}})}}\,\,{\text{при}}\,\,{{k}_{1}} = {{k}_{{ - 1}}}.$

Линейное время релаксации к этому равновесию, определяемое выражением (8), равно

(1.5)
$\tau = {1 \mathord{\left/ {\vphantom {1 {(4{{k}_{1}}{{A}_{\infty }} + 4{{k}_{{ - 1}}}(1 - {{A}_{\infty }})}}} \right. \kern-0em} {(4{{k}_{1}}{{A}_{\infty }} + 4{{k}_{{ - 1}}}(1 - {{A}_{\infty }})}} + {{k}_{2}} + {{k}_{{ - 2}}}).$

Среднее и быстрое времена релаксации, определяемые выражениями (9), (10), в общем случае определяются громоздкими выражениями, поэтому приведем их только для равновесия (1.4) при k1 = k2 = k−1 = k−2:

(1.6)
${{\tau }_{{a{v}}}}\sim {1 \mathord{\left/ {\vphantom {1 {{{k}_{1}}}}} \right. \kern-0em} {{{k}_{1}}}},\,\,\,\,{{\tau }_{{fast}}}\sim {{t}_{{resp}}}\sim {{10}^{{ - 3}}}.$

Критерий существования быстрых релаксаций (11) или (12), (13) по любому реагенту запишется как (4k1A + k–2)A' = (4k–1B + k2)B ' и с учетом ЗС в дифференциальной форме: A ' + B ' = 0, примет вид

(1.7)
$4{{k}_{1}}A + 4{{k}_{{ - 1}}}B + {{k}_{2}} + {{k}_{{ - 2}}} = 0.$

Это равенство не выполняется ни при каких физичных значениях кинетических параметров и концентраций реагентов. Следовательно, в этой реакции быстрые релаксации не возникают, и весь переходный процесс хорошо наблюдается независимо от параметров оборудования.

Пример 2. Пусть реакция A = С протекает в закрытой системе по нелинейной последовательной схеме

(2.1)
$2{\text{A}} = 2{\text{B}},\,\,\,\,{\text{B}} = {\text{C}},$

где A, B и C – реагенты. Ее динамическая модель (2) имеет вид

(2.2)
$\begin{gathered} A{\kern 1pt} ' = - 2{{k}_{1}}{{A}^{2}} + 2{{k}_{{ - 1}}}{{B}^{2}}, \\ B{\kern 1pt} ' = 2{{k}_{1}}{{A}^{2}} - 2{{k}_{{ - 1}}}{{B}^{2}} - {{k}_{2}}B + {{k}_{{ - 2}}}С, \\ С{\kern 1pt} ' = {{k}_{2}}B - {{k}_{{ - 2}}}C. \\ \end{gathered} $

В этой реакции при начальных условиях A0 = 1, B0 = 0, С0 = 0 выполняется ЗС A + B + C = A0 + B0+ + C0 = 1. С его учетом в равновесии (4) система (2.2) запишется как k1A2 = k–1(1 – A – С)2, k2(1 – ‒ A – С) = k–2С. Отсюда с учетом (5)–(7) в общем случае следует наличие единственного детального устойчивого равновесия типа “узел”:

(2.3)
$\begin{gathered} {{A}_{\infty }} = {1 \mathord{\left/ {\vphantom {1 {(1 + a + ab)}}} \right. \kern-0em} {(1 + a + ab)}},\,\,\,\,{{C}_{\infty }} = {{{{k}_{2}}(1 - {{A}_{\infty }})} \mathord{\left/ {\vphantom {{{{k}_{2}}(1 - {{A}_{\infty }})} {({{k}_{2}} + {{k}_{{ - 2}}})}}} \right. \kern-0em} {({{k}_{2}} + {{k}_{{ - 2}}})}}, \\ {{B}_{\infty }} = 1 - {{A}_{\infty }} - {{С}_{\infty }}\,\,{\text{при}}\,\,{{k}_{ - }}_{1} \ne 0,\,\,\,\,{{k}_{ - }}_{2} \ne 0, \\ \end{gathered} $

где α ≡ (k1/k–1)1/2, β ≡ k2/k–2. В частном случае при k–1 = 0 координаты равновесия равны A∞ = 0, B∞ = k–2/(k2 + k–2), C∞ = k2/(k2 + k–2). В общем случае времена релаксации (8)–(10) определяются громоздкими выражениями, поэтому приведем их только при k1 = k2 = k–1 = k–2:

(2.4)
$\tau \approx {{0.9} \mathord{\left/ {\vphantom {{0.9} {{{k}_{1}}}}} \right. \kern-0em} {{{k}_{1}}}},\,\,\,\,{{\tau }_{{{\text{ср}}}}}\sim {1 \mathord{\left/ {\vphantom {1 {{{k}_{1}}}}} \right. \kern-0em} {{{k}_{1}}}},\,\,\,\,{{\tau }_{{fast}}}\sim {{10}^{{ - 3}}}.$

Критерий быстрых релаксаций (12), (13) по A, B и С запишется соответственно как A" = –4k1AA' + + 4k–1BB ' = 0, A → 1, B" = 4k1AA' – 4k–1BB ' – k2B ' + + k–2С ' = 0, B → 0 и С" = k2B' – k−2C ' = 0, С → 0, или

(2.5)
${{k}_{1}}A{\kern 1pt} ' = {{k}_{{ - 1}}}B{\kern 1pt} ',$
(2.6)
$4{{k}_{1}}AA{\kern 1pt} '\, + {{k}_{{ - 2}}}С{\kern 1pt} ' = (4{{k}_{{ - 1}}}B + {{k}_{2}})B{\kern 1pt} ',$
(2.7)
${{k}_{2}}B{\kern 1pt} ' = {{k}_{{ - 2}}}C{\kern 1pt} '.$

Вблизи н.у. скорости изменения исходных веществ и продуктов должны иметь противоположные знаки, т.е. должны выполняться следующие “стартовые” условия:

(2.8)
$A{\kern 1pt} ' \to - 2{{k}_{1}} < 0,\,\,\,\,B{\kern 1pt} ' \to 2{{k}_{1}} > 0,\,\,\,\,С{\kern 1pt} ' \to + 0.$

Символ “→ +0” означает стремление к нулю сверху (оставаясь неотрицательным: ≥0). Условия (2.8) противоречат (2.5), но не противоречат (2.6) или (2.7). Следовательно, быстрые релаксации по исходному веществу А не возможны, а по продуктам B и С – возможны (рис. 1, 2).

Рис. 1.

Кинетика реакции (2.1) в замедленной “съемке” при k1 = k2 = k–1 = k–2 = 103: 1 – A(t), 2 – B(t), 3 – C(t).

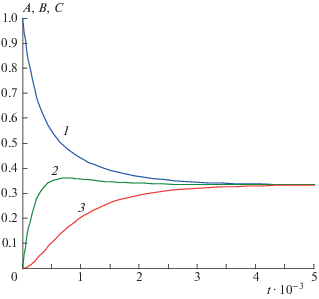
Рис. 2.

Ускорения реагентов реакции (2.1) при k1 = k2 = = k–1 = k–2 = 103: 1 – A "(t), 2 – B "(t), 3 – C "(t).

Из рис. 1, 2 видно, что при выбранных значениях кинетических параметров кривые зависимостей A(t) и A "(t) монотонны без перегибов (“спуски”), а кривые зависимостей B(t) и B"(t), C(t) и C "(t) проходят через “холмы”, “овраги” и “волны”. Анализ показал что при вариации кинетических параметров ситуация качественно не меняется, что подтверждает наличие периода быстрых релаксаций только для продуктов реакции. Отметим, что в зависимости от стехиометрических чисел стадий, брутто-уравнение схемы реакции (2.1) может быть различным: A = С или 2А = B + С и т.д. Это означает, что критерий быстрых релаксаций (2.5)–(2.7) применим ко всем реакциям, протекающим по схеме (2.1) .

Пример 3. Пусть гетерогенная реакция A = B протекает в открытой системе по схеме

(3.1)
${\text{A}} + {\text{Z}} = {\text{X}},\,\,\,\,{\text{X}} = {\text{Z}} + {\text{B}},$

где А, В и Х, Z – основные и промежуточные вещества. Для нее модель (2), (3) запишется в виде

(3.2)
$\begin{gathered} A{\kern 1pt} ' = - {{k}_{1}}Az + {{k}_{{ - 1}}}x + {{q}^{0}}{{A}^{0}} - qA, \\ B{\kern 1pt} ' = {{k}_{2}}x - {{k}_{{ - 2}}}zB + {{q}^{0}}{{B}^{0}} - qB. \\ \end{gathered} $
(3.3)
$x{\kern 1pt} ' = {{k}_{1}}Az - {{k}_{{ - 1}}}x - {{k}_{2}}x{\text{ }} + {\text{ }}{{k}_{{ - 2}}}zB,\,\,\,\,x + z = 1,$

где A0 = 1, B0 = 0 на входе, а A0 = 1, B0 = 0, x0 = 0, z0 = 1 – начальные условия. В равновесии

(3.4)
$\begin{gathered} {{k}_{1}}Az - {{k}_{{ - 1}}}x = {{q}^{0}}{{A}^{0}} - qA, \\ - ({{k}_{2}}x - {{k}_{{ - 2}}}zB) = {{q}^{0}}{{B}^{0}} - qB, \\ {{k}_{1}}Az - {{k}_{{ - 1}}}x = {{k}_{2}}x - {{k}_{{ - 2}}}zB, \\ \end{gathered} $

откуда находим координаты единственного физичного равновесия:

(3.5)
$\begin{gathered} {{A}_{\infty }} = {{({{k}_{{ - 1}}}x + {{q}^{0}}{{A}^{0}})} \mathord{\left/ {\vphantom {{({{k}_{{ - 1}}}x + {{q}^{0}}{{A}^{0}})} {\left( {{{k}_{1}}z + q} \right)}}} \right. \kern-0em} {\left( {{{k}_{1}}z + q} \right)}}, \\ {{B}_{\infty }} = {{({{k}_{2}}x + {{q}^{0}}{{B}^{0}})} \mathord{\left/ {\vphantom {{({{k}_{2}}x + {{q}^{0}}{{B}^{0}})} {({{k}_{{ - 2}}}z + q)}}} \right. \kern-0em} {({{k}_{{ - 2}}}z + q)}}, \\ {{х}_{\infty }} = {{\left[ {b - {{{({{b}^{2}} - 4ac)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right]} \mathord{\left/ {\vphantom {{\left[ {b - {{{({{b}^{2}} - 4ac)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right]} {2a}}} \right. \kern-0em} {2a}}, \\ \end{gathered} $

где

$\begin{gathered} a = ({{k}_{1}}{{k}_{2}} + {{k}_{{ - 1}}}{{k}_{{ - 2}}})q + {{k}_{1}}{{k}_{{ - 2}}}{{q}^{0}}, \\ b = ({{k}_{1}}{{k}_{2}} + {{k}_{{ - 1}}}{{k}_{{ - 2}}})q + ({{k}_{{ - 1}}} + {{k}_{2}}){{q}^{2}} \\ + \,\,({{k}_{1}}{{A}^{0}} + {{k}_{{ - 2}}}{{B}^{0}})q{{q}^{0}} + {\text{ }}2{{k}_{1}}{{k}_{{ - 2}}}{{q}^{0}}, \\ c = ({{k}_{1}}{{A}^{0}} + {{k}_{{ - 2}}}{{B}^{0}})q{{q}^{0}} + {{k}_{1}}{{k}_{{ - 2}}}{{q}^{0}}. \\ \end{gathered} $

Времена релаксации (8)–(10) к этому равновесию выражаются громоздкими соотношениями, поэтому приведем выражения для них при k±i ∼ k1 и q ∼ 1:

(3.6)
$\tau = {1 \mathord{\left/ {\vphantom {1 {[{{k}_{1}}(1 - {{х}_{\infty }}) + q]}}} \right. \kern-0em} {[{{k}_{1}}(1 - {{х}_{\infty }}) + q]}},$
(3.7)
${{\tau }_{{a{v}}}}\sim {1 \mathord{\left/ {\vphantom {1 {{\text{min}}}}} \right. \kern-0em} {{\text{min}}}}\left( {q,{{k}_{1}}} \right),\,\,\,\,{{\tau }_{{fast}}}\sim {{10}^{{ - 3}}}.$

Критерий быстрых релаксаций (12), (13) по продуктам A, B и X запишется соответственно как A " = –k1A'z – k1Az' + k–1x' – qA' = 0, A → 1; B " = k2x' – – k−2z'B – k–2zB' – qB' = 0, B → 0; x" = k1A'z + k1Az' – – k–1x' – k2x' + k–2z'B + k–2zB ' = 0, x → 0, или

(3.8)
$\left( {{{k}_{1}}z + q} \right)A{\kern 1pt} ' = ({{k}_{1}}A + {{k}_{{ - 1}}})x{\kern 1pt} ',$
(3.9)
$({{k}_{{ - 2}}}z + q)B{\kern 1pt} ' = ({{k}_{2}} + {{k}_{{ - 2}}}B)x{\kern 1pt} ',$
(3.10)
$({{k}_{1}}A{\kern 1pt} ' + {{k}_{{ - 2}}}B{\kern 1pt} ')z = ({{k}_{{ - 1}}} + {{k}_{2}} + {{k}_{1}}A + {{k}_{{ - 2}}}B)x{\kern 1pt} '.$

Вблизи н.у. должны выполняться следующие “стартовые” условия:

(3.11)
$\begin{gathered} A{\kern 1pt} ' = {{q}^{0}}{{A}^{0}} - \left( {{{k}_{1}} + q} \right) \ne 0, \\ B{\kern 1pt} ' \to {{q}^{0}}{{B}^{0}} > 0,\,\,\,\,x{\kern 1pt} ' \to {{k}_{1}} > 0. \\ \end{gathered} $

Условия (3.11) не противоречат ни одному из равенств (3.8)–(3.10). Значит, быстрые релаксации возможны по всем реагентам (рис. 3, 4).

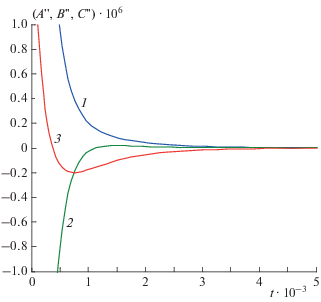
Рис. 3.

Кинетика реакции (3.1) в замедленной “съемке” при k1 = 103, k2 = 104, k–1 = 103, k–2 = 5 ⋅ 103, q = = 2 ⋅ 103, q0 = 103: 1 – A(t), 2 – B(t), 3 – x(t).

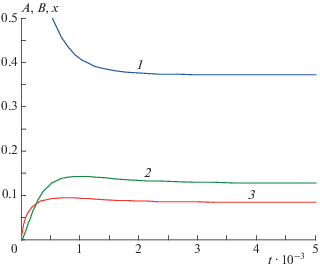
Рис. 4.

Ускорения реагентов реакции (3.1) при k1 = 103, k2 = 104, k–1 = 103, k–2 = 5 ⋅ 103, q = 2 ⋅ 103, q0 = 103: 1 – A"(t), 2 – B "(t), 3 – x"(t).

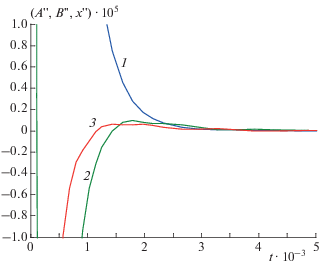
Из рис. 3, 4 видно, что при выбранных значениях кинетических параметров кривые зависимостей A(t) и A "(t) монотонны без перегибов (“спуски”), а концентрационные кривые продуктов проходят через один “холм” и одну “волну” вниз. Однако анализ показал, что при других (например, равных) значениях кинетических параметров концентрационная кривая исходного реагента А может проходить через один “овраг” и одну “волну” вверх, а концентрационные кривые продуктов B и X при этом изменяются монотонно без перегибов (“подъемы”). Это подтверждает наличие периода быстрых релаксаций по всем реагентам.

Пример 4. Пусть реакция 2A = B + C протекает по параллельной схеме:

(4.1)
${\text{A}} = {\text{B}},\,\,\,\,{\text{A}} = {\text{C}},$

где А, В и C – основные вещества. Для нее модель (2), (3) в закрытой системе запишется соответственно как

(4.2)
$\begin{gathered} A{\kern 1pt} ' = - {{k}_{1}}A + {{k}_{{ - 1}}}B - {{k}_{2}}A + {{k}_{{ - 2}}}C, \\ B{\kern 1pt} ' = {{k}_{1}}A - {{k}_{{ - 1}}}B,\,\,\,\,C{\kern 1pt} ' = {{k}_{2}}A - {{k}_{{ - 2}}}C, \\ \end{gathered} $

где A0 = 1, B0 = 0, C0 = 0 – начальные условия и A + + B + C = A0 + B0 + C0 = 1 – закон сохранения. В равновесии

(4.3)
$\begin{gathered} {{A}_{\infty }} = {{{{k}_{{ - 1}}}{{k}_{{ - 2}}}} \mathord{\left/ {\vphantom {{{{k}_{{ - 1}}}{{k}_{{ - 2}}}} K}} \right. \kern-0em} K},\,\,\,\,{{B}_{\infty }} = {{{{k}_{1}}{{k}_{{ - 2}}}} \mathord{\left/ {\vphantom {{{{k}_{1}}{{k}_{{ - 2}}}} K}} \right. \kern-0em} K}, \\ {{С}_{\infty }} = {{{{k}_{{ - 1}}}{{k}_{2}}} \mathord{\left/ {\vphantom {{{{k}_{{ - 1}}}{{k}_{2}}} K}} \right. \kern-0em} K},\,\,\,\,K \equiv {{k}_{1}}{{k}_{{ - 2}}} + {{k}_{ - }}_{1}{{k}_{2}} + {{k}_{{ - 1}}}{{k}_{{ - 2}}}. \\ \end{gathered} $

Времена релаксации (8)–(10) к этому равновесию равны (при k±I ∼ k1)

(4.4)
$\tau = {{\text{2}} \mathord{\left/ {\vphantom {{\text{2}} {{{{\{ {{k}_{{\text{1}}}} + {{k}_{{\text{2}}}} + {{k}_{{ - {\text{1}}}}} + {{k}_{{ - {\text{2}}}}} - [{{{({{k}_{{\text{1}}}} + {{k}_{{ - {\text{1}}}}})}}^{{\text{2}}}} + {{{(k_{{\text{2}}}^{{\text{2}}} + {{k}_{{ - {\text{2}}}}})}}^{{\text{2}}}} - {\text{2}}{{k}_{{\text{1}}}}{{k}_{{ - {\text{2}}}}} - {\text{2}}{{k}_{{ - {\text{1}}}}}{{k}_{{\text{2}}}} - {\text{2}}{{k}_{{ - {\text{1}}}}}{{k}_{{ - {\text{2}}}}})]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\} }}} \right. \kern-0em} {{{{\{ {{k}_{{\text{1}}}} + {{k}_{{\text{2}}}} + {{k}_{{ - {\text{1}}}}} + {{k}_{{ - {\text{2}}}}} - [{{{({{k}_{{\text{1}}}} + {{k}_{{ - {\text{1}}}}})}}^{{\text{2}}}} + {{{(k_{{\text{2}}}^{{\text{2}}} + {{k}_{{ - {\text{2}}}}})}}^{{\text{2}}}} - {\text{2}}{{k}_{{\text{1}}}}{{k}_{{ - {\text{2}}}}} - {\text{2}}{{k}_{{ - {\text{1}}}}}{{k}_{{\text{2}}}} - {\text{2}}{{k}_{{ - {\text{1}}}}}{{k}_{{ - {\text{2}}}}})]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\} }},$
(4.5)
${{\tau }_{{a{v}}}}\sim {1 \mathord{\left/ {\vphantom {1 {{\text{min}}}}} \right. \kern-0em} {{\text{min}}}}({{k}_{i}}),\,\,\,\,{{\tau }_{{fast}}}\sim {{10}^{{ - 3}}}.$

Критерий быстрых релаксаций (12), (13) по продуктам A, B и С запишется соответственно как A"= –k1A' + k–1B' – k2A' + k–2C ' = 0, A → 1; B" = k1A' – – k–1B' = 0, B → 0; C" = k2A' – k−2C ' = 0, C → 0, или с учетом ЗС

(4.6)
$ - {{k}_{1}}A{\kern 1pt} '\,\, + {{k}_{{ - 1}}}B{\kern 1pt} '\,\, - {{k}_{2}}A{\kern 1pt} '\,\, + {{k}_{{ - 2}}}C{\kern 1pt} ' = 0,$
(4.7)
${{k}_{1}}A{\kern 1pt} ' = {{k}_{{ - 1}}}B{\kern 1pt} ',$
(4.8)
${{k}_{2}}A{\kern 1pt} ' = {{k}_{{ - 2}}}C{\kern 1pt} '.$

Вблизи н.у. должны выполняться следующие “стартовые” условия:

(4.9)
$\begin{gathered} A{\kern 1pt} ' \to - \left( {{{k}_{1}} + {{k}_{2}}} \right) < 0, \\ B{\kern 1pt} ' \to {{k}_{1}} > 0,\,\,\,\,С{\kern 1pt} ' \to {{k}_{2}} > 0. \\ \end{gathered} $

Условия (4.9) противоречат всем равенствам (4.6)–(4.8), значит быстрые релаксации невозможны ни по одному из реагентов, рис. 5, 6.

Рис. 5.

Кинетика реакции (4.1) в замедленной “съемке” при k1 = 103, k2 = 102, k–1 = 10, k–2 = 1: 1 – A(t), 2 – B(t), 3 – С(t).

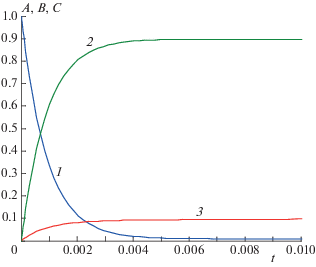
Рис. 6.

Ускорения реагентов реакции (4.1) при k1 = k2 = = k–1 = k–2 = 103: 1 – A"(t), 2 – B"(t), 3 – С"(t).

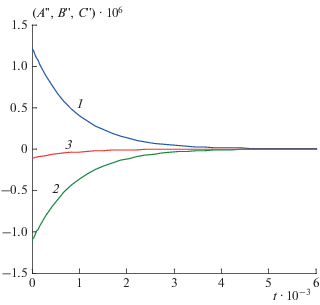
Все кинетические кривые на рис. 5, 6 изменяются монотонно без перегибов (“спуски” и “подъемы”). Анализ показал, что при других значениях кинетических параметров они не изменяются качественно, т.е. периода быстрых релаксаций ни по одному реагенту нет. Подчеркнем, что если эта же реакция: 2A = B + C, протекает по схеме (2.1) , то быстрые релаксации уже невозможны (см. Пример 2). Это объясняется тем, что критерий быстрых релаксаций привязан к схеме реакции, а не к ее брутто-уравнению.

ЗАКЛЮЧЕНИЕ

В нестационарных кинетических экспериментах по мере удаления от равновесия полезно выделять три качественно различных типа релаксационных процессов – медленные, средние и быстрые. Медленные (близкие к равновесию) и средние (более удаленные от равновесия) релаксации хорошо известны и описаны в литературе. Быстрые релаксации, наиболее удаленные от равновесия и, соответственно, близкие к начальным условиям реакции, ранее в литературе не упоминались. Быстрые релаксации могут наблюдаться, если значения кинетических параметров превышают разрешающие возможности оборудования, что затрудняет возможность их наблюдения. В данной работе получен стехиометрический критерий возникновения периода быстрых релаксаций, который позволяет априори установить возможность их существования и условия экспериментального наблюдения. Если этот критерий выполняется, то в течение этого периода обязательно существуют три информативные формы кинетических кривых (“овраги”, “холмы”, “волны”), которые несут дополнительную информацию о механизме исследуемой реакции. Полученные результаты расширяют понимание особенностей осуществления переходных процессов нелинейных химических реакций и могут быть полезны при решении обратных задач химической кинетики с использованием неравновесных экспериментов и оборудования с высоким разрешением.

Автор выражает благодарность В.Х. Федотову за полезные обсуждения результатов работы.

Список литературы

  1. Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний. М.: Наука, 1981.

  2. Вольтер Б.В., Сальников И.Е. Устойчивость режимов работы химических реакторов. М.: Химия, 1981.

  3. Николис Г., Пригожин И. Самоорганизация в неравновесных системах: От диссипативных структур к упорядоченности через флуктуации. М.: Мир, 1979.

  4. Киперман C.Л. Основы химической кинетики в гетерогенном катализе. М.: Химия, 1979.

  5. Яблонский Г.С., Быков В.И., Елохин В.И. Кинетика модельных реакций гетерогенного катализа. Новосибирск: Наука, 1984.

  6. Горбань А.Н. Обход равновесия (уравнения химической кинетики и их термодинамический анализ). Новосибирск: Наука, 1984.

  7. Быков В.И., Цыбенова С.Б. Нелинейные модели химической кинетики. М.: КРАСАНД, 2011.

  8. Быков В.И. Моделирование критических явлений в химической кинетике. М.: URSS, 2014.

  9. Bykov V.I., Tsybenova S.B., Yablonsky G.S. Chemical complexity via simple models. Berlin. New York: Germany. De Gruyter, 2018.

  10. Зельдович Я.Б. Избранные труды. Химическая физика и гидродинамика. М.: Наука, 1984. С. 43.

  11. Кольцов Н.И., Алексеев Б.В., Федотов В.Х. // ДАН СССР. 1991. Т. 317. № 1. С. 147.

  12. Кольцов Н.И., Федотов В.Х., Алексеев Б.В. // ДАН СССР. 1991. Т. 318. № 5. С. 1179.

  13. Кольцов Н.И., Федотов В.Х., Алексеев Б.В. // Прямые и обратные задачи в химической кинетике. Новосибирск: Наука, 1993. С. 175.

  14. Кольцов Н.И., Алексеев Б.В., Федотов В.Х. // ЖФХ. 1997. Т. 71. № 4. С. 758.

  15. Федотов В.Х., Кольцов Н.И., Алексеев Б.В. // ЖФХ. 1987. Т. 61. № 5. С. 1399.

  16. Constales D., Yablonsky G.S., Marin G.B. // Comp. and Math. with Applic. 2013. V. 65. № 10. P. 1614.

  17. Yablonsky G.S. // Theor. Found. Chem. Eng. 2014. V. 48. № 5. P. 608.

  18. Branco-Pinto D., Yablonsky G., Marin G., Constales D. // Entropy. 2015. V. 17. N 10. P. 6783.

  19. Горбань А.Н., Быков В.И., Яблонский Г.С. Очерки о химической релаксации. Новосибирск: Наука, 1986.

  20. Алексеев Б.В., Федотов В.Х., Кольцов Н.И., Киперман С.Л. // Хим. физика. 1982. Т. 1. № 6. С. 776.

  21. Федотов В.Х., Кольцов Н.И., Киперман С.Л. // Изв. ВУЗов. Хим и хим. технол. 1985. Т. 28. № 12. С. 38.

  22. Кольцов Н.И., Федотов В.Х., Алексеев Б.В., Киперман С.Л. // Изв. ВУЗов. Хим. и хим. технол. 1987. Т. 30. № 5. С. 57.

  23. Kol’tsov N.I., Fedotov V.Kh. // Surf. Sci. 1988. V. 206. № 3. P. 518.

  24. Кольцов Н.И., Федотов В.Х., Алексеев Б.В. Математические методы в химической кинетике. Новосибирск: Наука, 1990.

  25. Федотов В.Х., Кольцов Н.И. Хим. физика. 2014. Т. 33. № 6. С. 18.

  26. Кольцов Н.И., Алексеев Б.В. // Сообщ. по кинетике и катализу. 1984. Т. 24. № 3–4. С. 309.

  27. Федотов В.Х., Кольцов Н.И. // Изв. вузов. Химия и хим. технол. 2014. Т. 57. № 2. С. 63.

  28. Боднева В.Л., Иванов Г.К., Шуб Б.Р. // Хим. физика. 2004. Т. 23. № 6. С. 24.

  29. Харламов В.Ф., Харламов Ф.В. // Хим. физика. 2008. Т. 27. № 2. С. 47.

  30. Москаленко А.С., Уманский С.Я. // Хим. физика. 2012. Т. 31. № 2. С. 61.

  31. Мешков Д.А., Иванов В.А., Нечаев С.К., Аветисов В.А. // Хим. физика. 2014. Т. 33. № 7. С. 47.

  32. Григорян Г.М., Ткаченко Т.Л. // Хим. физика. 2017. Т. 36. № 2. С. 18.

  33. Корн Г., Корн Т. Справочник по математике. М.: Наука. 1978. 831 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Химическая физика

Архивы выпусков Информация о журнале Отправить рукопись в журнал