1. На главную
  2. Электронные версии
  3. Химическая физика
  4. T. 39, № 9, 2020

Химическая физика, 2020, T. 39, № 9, стр. 18-22

Математическое моделирование процесса окисления дисперсного алюминия водой

Н. С. Шайтура 1, *, М. Н. Ларичев 1

1 Федеральный исследовательский центр химической физики им. Н.Н. Семёнова Российской академии наук
Москва, Россия

* E-mail: tesh-s@yandex.ru

Поступила в редакцию 19.06.2019
После доработки 11.07.2019
Принята к публикации 22.07.2019

Полный текст (PDF)

Аннотация

Заметный интерес к практическому использованию процесса окисления дисперсного алюминия водой как к источнику газообразного водорода для нужд водородной энергетики обусловливает необходимость не только понимания механизма процесса, но и возможность его математического моделирования. Такое моделирование выполнено в настоящей работе благодаря проведенному ранее авторами экспериментальному изучению кинетики и механизма процесса окисления дисперсного алюминия водой. Предложена модель процесса окисления, найдены эффективные энергии активации процессов, протекающих при окислении алюминия. Полученная модель позволила не только предсказывать скорости окисления алюминия водой в диапазоне температур 50–100 °C, но и уточнить механизм процесса.

Ключевые слова: окисление Al, водород, водородная энергетика, гидроксид алюминия, математическое моделирование.

ВВЕДЕНИЕ

Процесс окисления металлического алюминия водой привлекает внимание исследователей во многом как перспективный источник газообразного водорода для нужд водородной энергетики [1]. Изучению различных аспектов этого процесса посвящено заметное количество работ, выполняемых в ведущих научных центрах многих стран мира [2–6]. В опубликованной авторами работе [6] был изучен механизм процесса низкотемпературного (до 100 °С) окисления дисперсного Al водой. Такое низкотемпературное окисление Al представляется наиболее безопасным для потребителя, легко реализуемым и может быть рекомендовано для использования при конструировании энергетических устройств широкого профиля.

Цель данной работы – проведение математического моделирования процесса низкотемпературного окисления алюминия водой для оценки возможности расчетов при планировании экспериментов и конструировании экспериментального оборудования. Моделирование проводили с использованием полученных в работе [6] экспериментальных данных и установленного механизма процесса окисления.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

В работе исследовалось окисление дистиллированной водой дисперсного алюминиевого порошка марки АСД-4 (ТУ 48-5-226-87) со средним размером сферических частиц около 4 мкм, серийно производимого российской промышленностью. Для моделирования процесса низкотемпературного окисления использовали полученные нами в работе [6] экспериментальные данные, а оборудование и методика эксперимента описаны в работах [6, 7]. Кинетические кривые скорости выделения водорода снимались при постоянной температуре (в изотермическом режиме). В ходе эксперимента температура в реакторе поддерживалась постоянной за счет системы термостатирования.

Скорость процесса окисления металлического алюминия определяли путем измерения скорости образования водорода, поток которого, вытекающий из реактора, измеряли с помощью расходомеров фирмы Aalborg (США). Полученные кинетические зависимости скорости образования водорода интегрировались в программе ORIGIN. Степень окисления алюминия определяли как отношение объема суммарно выделившегося на данный момент водорода к количеству водорода, соответствующее полному окислению алюминия. Численное моделирование процесса окисления проводили с использованием программы Thermokinetics 3 фирмы Netzch (Германия), предназначенной для кинетического расчета тепловых измерений. Программа позволяет обрабатывать различного рода данные, в том числе полученные при измерениях методами термогравиметрии, дифференциального термического анализа, дифференциальной сканирующей калориметрии, масс-спектрометрии, дилатометрии или реометрии.

МОДЕЛИРОВАНИЕ

Как было установлено ранее [1] из анализа кривых скорости образования водорода, процесс окисления дисперсного алюминия можно разделить на несколько последовательных стадий: стадию начального окисления, стадию индукции, стадию интенсивного окисления и стадию затухания реакции. Подробно процессы, протекающие на каждой из этих стадий, изучены в работе [6]. В отсутствие активации, т.е. при использовании для окисления дистиллированной воды, скорость окисления алюминия на стадии начального окисления очень низкая и, как правило, сравнима с чувствительностью используемого для измерения скорости образования водорода оборудования; при протекании этой стадии окисляется, как правило, меньше нескольких процентов металла. По этой причине при моделировании процесса окисления стадия начального окисления в отсутствие активации не учитывалась, и моделирование проводили, начиная со стадии индукции, во время которой протекает гидролиз оксидного покрытия на частицах алюминия. Как показано нами в работе [6], процесс гидролиза начинается локально в наиболее дефектных местах оксидного покрытия, затем наблюдается рост гидролизованной поверхности. Гетерогенные процессы, которые идут по механизму образования, роста и столкновения зародышей, обычно описываются уравнением Аврами–Ерофеева [8], которое в дифференциальной форме имеет вид

(1)
$--\frac{{de}}{{dt}} = A~n~e{{\left( {--\ln e} \right)}^{{\left( {n--1} \right)/n}}}{\text{exp}}\left( {--\frac{{{{E}_{A}}}}{{R~T}}} \right),$
где A – предэкспоненциальный фактор, EА – энергия активации, e – концентрация исходного реагента, n – кинетический параметр, T – температура, R – универсальная газовая постоянная.

После окончания периода индукции (окончания гидролиза пассивирующего покрытия) гидролизованное оксидное покрытие становится проницаемым для молекул воды, что делает возможной химическую реакцию металлического алюминия с водой. В качестве твердого продукта реакции образуется гидроксид алюминия, который накапливается на окисляемой поверхности алюминия в виде золь-геля. В зависимости от условий проведения процесса, в частности от температуры реакционной среды, возможны варианты: образующаяся оболочка хорошо проницаема для воды и тогда процесс окисления протекает в кинетическом режиме, т.е. может быть описан реакцией n-го порядка; образующаяся оболочка слабо проницаема для воды и тогда процесс протекает в диффузионном режиме, т.е. может быть описан с помощью диффузионной модели. Изменение условий протекания окисления может приводить к смене режима процесса (кинетический переходит в диффузионный или наоборот). Таким образом, в реакционной среде могут протекать два параллельных процесса. Модель процесса окисления приведена ниже:

(2)
$a \to b\left| \begin{gathered} \to c \hfill \\ \to d \hfill \\ \end{gathered} \right.,$

где a – доля алюминиевых частиц “в состоянии поставки”, вступающих во взаимодействие с водой (за единицу принята начальная концентрация алюминиевых частиц в реакционной смеси); b – доля алюминиевых частиц с полностью гидратированным оксидным покрытием, но еще неокисленным алюминием; c – доля окисленных в кинетическом режиме алюминиевых частиц; d – доля окисленных в диффузионном режиме алюминиевых частиц.

Необходимо отметить, что, поскольку алюминиевый порошок в исходном состоянии имеет распределение частиц по размерам и по толщине пассивирующего покрытия, то разные частицы вступают в реакцию неодновременно. Процесс гидролиза, а также процесс окисления металла – гетерогенные процессы, идущие на поверхности частицы. Это означает, что для каждой частицы доля прореагировавшей поверхности может несколько отличаться от среднего значения a; например, на одной частице может гидролизоваться половина ее поверхности, а на другой – всего несколько процентов.

Этой модели соответствует система дифференциальных уравнений

$\begin{gathered} \frac{{da}}{{dt}} = - {{A}_{1}}\exp \left( { - \frac{{{{E}_{1}}}}{{RT}}} \right){{n}_{{\text{1}}}}a{{\left( { - {\text{ln}}a} \right)}^{{{{({{n}_{1}} - 1)} \mathord{\left/ {\vphantom {{({{n}_{1}} - 1)} {{{n}_{1}}}}} \right. \kern-0em} {{{n}_{1}}}}}}}, \\ \frac{{db}}{{dt}} = {{A}_{1}}\exp \left( { - \frac{{{{E}_{1}}}}{{RT}}} \right){{n}_{{\text{1}}}}a{{\left( { - {\text{ln}}a} \right)}^{{{{({{n}_{1}} - 1)} \mathord{\left/ {\vphantom {{({{n}_{1}} - 1)} {{{n}_{1}}}}} \right. \kern-0em} {{{n}_{1}}}}}}} - \\ - \,\,{{A}_{2}}\exp \left( { - \frac{{{{E}_{2}}}}{{RT}}} \right)b{}^{{{{n}_{2}}}} - {{A}_{3}}\exp \left( { - \frac{{{{E}_{3}}}}{{RT}}} \right){{f}_{3}}(b,d), \\ \frac{{dc}}{{dt}} = {{A}_{2}}\exp \left( { - \frac{{{{E}_{2}}}}{{RT}}} \right){{b}^{{{{n}_{2}}}}},\,\,\,\,d = 1 - a - b - c, \\ \end{gathered} $

где A1, A2, A3 – предэкспоненциальные множители, E1, E2, E3 – энергии активации, n1 – кинетический параметр в уравнении Аврами–Ерофеева, n2 – порядок реакции (2), T – температура, R – универсальная газовая постоянная,  f3 – функция, соответствующая одной из диффузионных моделей. Индекс “1” соответствует реакции a → b, индекс “2” – b → c, индекс “3” – b → d.

Для кинетического анализа в литературе широко используются как безмодельные, так и использующие конкретные математические модели методы. Безмодельные методы не могут быть использованы для параллельных реакций [9], поэтому был выбран метод, позволяющий сочетать различные модели процесса, реализованный в программе Thermokinetics 3, и способный выполнять анализ для параллельных процессов. Кинетический анализ может быть основан на моделях, описывающих процессы с одной, двумя, тремя или четырьмя стадиями и для каждого индивидуального шага связан с независимыми, параллельными, конкурирующими или последовательными реакциями.

Начальные условия (согласно программе Thermokinetics 3) были заданы следующим образом:

$\begin{gathered} {{a}_{0}} = 0.99990,\,\,\,\,{{b}_{0}} = 0.00008, \\ {{c}_{0}} = 0.00001,\,\,\,\,{{d}_{0}} = 0.00001. \\ \end{gathered} $

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Результаты моделирования показаны на рис. 1, а найденные параметры приведены в табл. 1. В данном случае для описания диффузии использовали алгоритм расчета, предложенный в работе [10], основанный на первом законе Фика. Следует отметить, что использование для обработки наших экспериментальных данных моделей Яндера (W.Z. Yander) и Гинслинга–Броунштейна (A.M. Ginstling, B.I. Brounstein) также позволяет достичь хорошего приближения к экспериментальным данным (коэффициенты корреляции для всех трех моделей лежат в диапазоне 0.9949–0.9963). На рис. 1 исходные экспериментальные зависимости обозначены пересеченными линиями, а смоделированные с помощью программы Thermokinetics 3 при различных температурах, в том числе при температурах, совпадающих с температурами экспериментов – сплошными линиями.

Рис. 1.

Экспериментальные кинетические кривые образования H2 при различных температурах (обозначены пересеченными линиями) и результаты математического моделирования процесса окисления с использованием предложенной модели (сплошные линии); цифрами у кривых показана температура в °C, при которой с помощью программы Thermokinetics 3 проводился (моделировался) процесс.

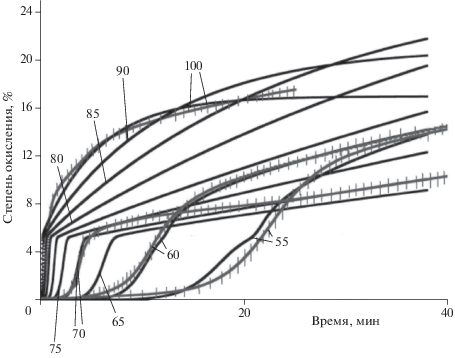
Таблица 1.  

Значения кинетических параметров, полученные в результате моделирования

1/log A1 E1, кДж/моль n1 1/log A2 E2, кДж/моль n2 1/log A3 E1, кДж/моль
11.1091 91.08 17.64 269.964 1743.15 24.14 19.777 166.77

В настоящей работе стандартное отклонение от экспериментальных данных для энергии активации гидролиза оксидного покрытия при использовании предложенной нами модели составляет 0.09 кДж/моль (0.1%); для энергии активации реакции, протекающей в кинетическом режиме – 10.5 кДж/моль (0.7%); для энергии активации реакции, протекающей в диффузионном режиме – 0.768 кДж/моль (0.4%). Поскольку экспериментальные результаты измерения скорости выделения водорода и температуры реакционной среды также имеют свои погрешности [7], то найденные при моделировании этих данных энергии активации имеют большую погрешность, чем отклонение модельных параметров от экспериментальных. По нашим оценкам, проведенным в работе [7], погрешность для энергии активации (с учетом экспериментальной погрешности определения скорости выделения водорода) составляет 15%.

В работе [7] методом формальной кинетики были рассчитаны эффективные энергии активации гидролиза оксидного покрытия и суммарных процессов, протекающих во время периода активного окисления (который начинается с момента фиксируемого газовыделения и заканчивается, когда скорость газовыделения падала в 10 раз по сравнению с максимальной). Для их оценки использовались те же экспериментальные данные (см. рис. 1), что и для разработки модели окисления в настоящей работе. Значение энергии активации гидролиза оксидного покрытия, полученное в работе [7], составило (121 ± 21) кДж/моль, а эффективная энергия активации за период активного окисления – (126 ± 21) кДж/моль. Таким образом, в пределах погрешностей найденные энергии активации гидролиза оксидного покрытия в работе [7] и в настоящей работе совпадают друг с другом. Согласно предложенной в данной работе модели, за период активного газовыделения могут протекать две параллельные реакции. Поскольку энергия активации реакции, протекающей в кинетическом режиме, значительно больше энергии активации, протекающей в диффузионном режиме, то последней можно пренебречь. Следовательно, суммарная энергия активации за период активного газовыделения, найденная по настоящей модели, составляет (166 ± 25) кДж/моль, что согласуется в пределах погрешностей со значением (126 ± 21) кДж/моль, полученным нами в работе [7].

Полученная математическая модель позволяет не только предсказывать кинетические особенности выделения водорода в диапазоне температур 50–100 °C без проведения соответствующих измерений, но и дает возможность лучше понимать изменение режима окисления в зависимости от температуры. На рис. 2 приведены зависимости относительных концентраций исходных реагентов и продуктов от времени в процессе окисления алюминия водой, полученные в результате моделирования. Из рис. 2 видно, что максимум кривой концентрации b совпадает по времени с полным расходованием концентрации a, время этого максимума коррелирует с временем стадии индукции (см. рис. 1). Очевидно, что максимум на кривой b определяет время, за которое протекает гидролиз оксидного покрытия. В предложенной модели гидролиз покрытия описывается уравнением Аврами–Ерофеева. Полученное значение параметра n1 больше единицы (табл. 1), что свидетельствует о том, что гидролиз протекает в кинетической области [8].

Рис. 2.

Изменение относительных концентраций исходных реагентов и продуктов реакции во времени в процессе окисления алюминия водой: a + b + c + d = = 100%; a – T = 55 °C, б – T = 60 °C, в – T = 100 °C. Получено с помощью программы Thermokinetics 3.

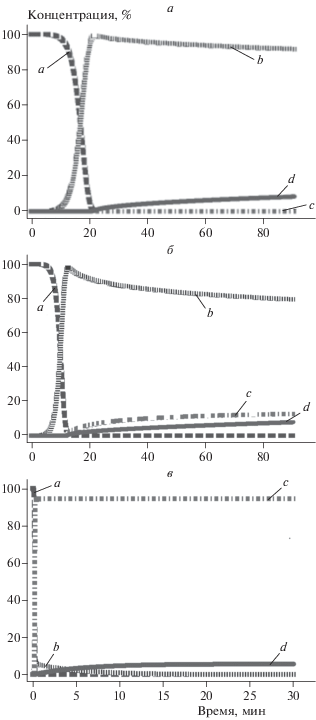
Относительное количество частиц Al c и d определяет режим, в котором протекает процесс окисления. Рисунок 2 показывает, что при повышении температуры диффузионный режим окисления переходит в кинетический. Так, при 55 °C (рис. 2а) алюминий окисляется в основном в диффузионном режиме. При температуре 60 °C (рис. 2б) процесс начинается преимущественно в кинетическом режиме, а затем кинетический режим постепенно переходит в диффузионный. При повышении температуры (вплоть до 100 °C, рис. 2в) доля окислившегося в кинетическом режиме алюминия увеличивается.

Следует отметить, что попытка применить разработанную модель для процесса окисления, протекающего с использованием активации (например, химической или ультразвуковой активации, используемых нами в работе [6]), не оказалась успешной. Возможно, использование активации приводит к изменению механизма процесса окисления и для моделирования окисления, протекающего в присутствии активации, необходимо использовать другую модель.

ЗАКЛЮЧЕНИЕ

В работе проведено моделирование процесса низкотемпературного окисления дисперсного алюминия водой. Это позволило не только предсказать кинетические особенности процесса окисления в диапазоне температур 50–100 °C, но и сделать заключение о переходе диффузионного режима окисления в кинетический с ростом температуры.

Авторы выражают благодарность разработчику программы Thermokinetics 3 Е. Мухиной за конструктивное обсуждение.

Список литературы

  1. Larichev M.N. // Metal Nanopowders: Production, Characterization, and Energetic Applications. Weinheim, Germany: Wiley-VCH Verlag GmbH & Co. KGaA, 2014. P. 163; https://doi.org/10.1002/9783527680696.ch8

  2. Wang H.Z., Leung D.Y.C., Leung M.K.H. et al. // Renew. Sustain. Energy Rev. 2009. V. 13. P. 845; https://doi.org/10.1016/j.rser.2008.02.009

  3. Soler L., Macanas J., Munoz M. et al. // J. Power Sources. 2007. V. 169. P. 144.

  4. Shkolnikov E.I., Zhuk A.Z., Vlaskin M.S. // Renew. Sustain. Energy Rev. 2009. V. 15. P. 4611; https://doi.org/10.1016/j.rser.2011.07.091

  5. Gromov A.A., Il’in A.P., Foerter-Barth U. et al. // Combust. Explos. Shock Waves. 2006. V. 42. № 2. P. 177.

  6. Шайтура Н.С., Ларичева О.О., Ларичев М.Н. // Хим. физика. 2019. Т. 38. № 3. С. 9; https://doi.org/10.1134/S0207401X19030087

  7. Ларичев М.Н., Шайтура Н.С., Колокольников В.Н. и др. // Изв. РАН. Энергетика. 2010. № 2. С. 85.

  8. Handbook of Thermal Analysis and Calorimetry. // Ed. Brown M.E. V. 1. Amsterdam: Elsevier, 1998.

  9. Moukhina E. // J. Therm. Anal. Calorim. 2012. V. 109. P. 1203; https://doi.org/10.1007/S10973-012-2406-3

  10. Serin B., Ellickson R.T. // J. Chem. Phys. 1941. V. 9. P. 742.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Химическая физика

Архивы выпусков Информация о журнале Отправить рукопись в журнал