Химическая физика, 2021, T. 40, № 11, стр. 3-8

Нелинейные кинетические законы сохранения в нелинейных химических реакциях

Н. И. Кольцов^*

Чувашский государственный университет им. И.Н. Ульянова
Чебоксары, Россия

Поступила в редакцию 20.11.2020
После доработки 16.02.2021
Принята к публикации 22.03.2021

DOI: 10.31857/S0207401X21110042

Аннотация

Разработан метод установления новых нелинейных кинетических законов сохранения в химических реакциях, протекающих в открытом изотермическом безградиентном реакторе по нелинейным механизмам, содержащим стадии превращения исходных веществ и не включающим стадии их образования. Эти законы есть разновидность мультиэкспериментных автономных кинетических инвариантов, которые можно получить на основе данных одного нестационарного эксперимента и использовать для решения обратной задачи конкретных нелинейных реакций.

Ключевые слова: нелинейные реакции, открытый безградиентный реактор, нелинейные кинетические законы сохранения.

ВВЕДЕНИЕ

Кинетические законы сохранения (КЗС) представляют собой наиболее сложные (не очевидные) комбинации нестационарных значений концентраций реагентов и кинетических параметров реакции, сохраняющие постоянные значения в течение всей реакции. Линейные КЗС (ЛКЗС) несложно обнаружить и точное их число для линейных и нелинейных реакций в закрытых системах известно [1–3]. Нелинейные КЗС (НКЗС) удалось обнаружить только для линейных и некоторых редко встречающихся классов нелинейных реакций и точное их число не известно даже для закрытых систем [4–7]. Однако для широкого класса нелинейных механизмов реакций НКЗС в настоящее время не обнаружены. Ниже приведен метод установления НКЗС в химических реакциях, протекающих в открытом изотермическом безградиентном реакторе по нелинейным механизмам, содержащим стадии превращения исходных веществ и не включающим стадии их образования. Рассмотрены примеры использования метода для установления НКЗС и их применения для идентификации механизмов конкретных реакций. Метод основан на мультиэкспериментном подходе, активно развиваемом в последнее время в зарубежной [8–12] и отечественной [13–19] научной литературе.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Пусть химическая реакция протекает через нелинейные стадии вида

(1)

$\sum\limits_i {{{a}_{{ij}}}{{{\mathbf{А}}}_{j}}} \Leftrightarrow \sum\limits_i {{{a}_{{ - ij}}}{{{\mathbf{А}}}_{j}}} ,\,\,\,\,i = 1,\,\, \ldots ,s,$

где a_ij, a_−ij − стехиометрические коэффициенты реагентов А_j, j = 1, …, n в левых и правых частях стадии i. Динамика такой реакции в открытом изотермическом безградиентном реакторе в рамках закона действующих масс описывается системой нелинейных обыкновенных дифференциальных уравнений (ОДУ):

(2)

$\begin{gathered} A_{j}^{'} = \sum\limits_i {\left( {{{a}_{{ - ij}}} - {{a}_{{ij}}}} \right)\left( {{{k}_{i}}\prod\limits_j {A_{j}^{{aij}}} - {{k}_{{ - i}}}\prod\limits_j {A_{j}^{{a - ij}}} } \right)} + \\ + \,\,{{q}_{0}}{{A}_{{0j}}} - q{{A}_{j}},\,\,\,\,j = 1,\,\, \ldots ,n, \\ \end{gathered} $

где А_j − концентрации реагентов А_j, мольн. доли; A_0j − начальные условия (н.у.); k_i, k_−i − константы скоростей стадий в прямом и обратном направлениях, 1/с; q₀ и q ≠ q₀ − начальная и текущая скорости реакционного потока.

Пусть хотя бы в одной из стадий (1) есть реагент A_k, который не взаимодействует с другими реагентами (назовем его свободным или free-реагентом). Это означает, что он участвует только в стадиях вида A_k → A_m, 2A_k → A_m, 2A_k → A_m + A_p + …, но не участвует в стадиях вида A_k + A_m → …. Условие существования таких реагентов в механизме реакции можно записать в виде

(3)

${{a}_{{i*k}}} \ne 0,\,\,\,\,{{a}_{{i*k}}}{{a}_{{i*j}}} = 0,\,\,\,\,{{k}_{{ - i*}}} = 0,$

где i* = i₁, i₂,… − номера стадий, в которых участвует free-реагент. Скорость образования каждого free-реагента зависит только от его концентрации A_k и кинетических параметров (констант скоростей стадий и скорости потока)

(4)

$\begin{gathered} A_{k}^{'} = \sum\limits_{i*} {({{a}_{{ - i*k}}} - {{a}_{{i*k}}})} {{k}_{{i*}}}\prod\limits_{jk} {A_{k}^{{ai*k}}} + \\ + \,\,{{q}_{0}}{{A}_{{0k}}} - q{{A}_{k}} \equiv {{f}_{k}}\left( {{{A}_{k}},{{A}_{{0k}}},q,{\text{ }}{{q}_{0}},{{k}_{{i*}}}} \right), \\ \end{gathered} $

где f_k − различные полиномы невысокой степени (т.к. молекулярность реакций, как правило, не превышает трех), вид которых определяется стехиометрией стадий (1). Уравнения (4) являются линейными, квадратичными или кубическими неоднородными ОДУ, которые не зависят друг от друга и интегрируются точно (уравнения Рикатти, Абеля и других) [20]. Запишем их решения в общем виде:

(5)

$\begin{gathered} {{A}_{k}}(t){\text{ }} = \int {{{f}_{k}}({{A}_{k}},q,{{k}_{i}}_{*})dt} \equiv {{F}_{k}}(t,q,{{k}_{{i*}}}) + {{C}_{k}}, \\ k \in [1,\,\, \ldots ,n], \\ \end{gathered} $

где t – время, c; C_k = C_k(q, k_i*, A_0k) − константы интегрирования. Сложим уравнения (2) и получим линейное относительно алгебраической суммы концентраций реагентов ОДУ:

(6)

$\sum\limits_j {{{\alpha }_{j}}A_{j}^{'}} = {{q}_{0}} - q\sum\limits_j {{{\alpha }_{j}}{{A}_{j}}} ,$

где α_j – константы, зависящие только от стехиометрических коэффициентов реагентов, причем $\sum\nolimits_j {{{\alpha }_{j}}{{A}_{{0j}}}} $ = 1 (константа нормирования). Уравнение (6) линейно относительно суммы $\sum\nolimits_j {{{\alpha }_{j}}{{A}_{j}}} ,$ так как константы α_j входят как одинаковые сомножители в обе части равенства (6). Заменим этим уравнением одно из уравнений (2) для реагента c индексом j ≠ k и получим систему ОДУ, эквивалентную исходной. Проинтегрируем (6) и найдем зависимость суммы значений концентраций реагентов от времени $q\sum\nolimits_j {{{\alpha }_{j}}{{A}_{j}}} $ = q₀ + (q – ‒ q₀)exp(−qt), откуда следует

(7)

$t = \ln {{\left\{ {{{({{q}_{0}} - q)} \mathord{\left/ {\vphantom {{({{q}_{0}} - q)} {\left[ {\left. {{{q}_{0}} - q\sum\limits_j {{{\alpha }_{j}}{{A}_{j}}} } \right)} \right]}}} \right. \kern-0em} {\left[ {\left. {{{q}_{0}} - q\sum\limits_j {{{\alpha }_{j}}{{A}_{j}}} } \right)} \right]}}} \right\}} \mathord{\left/ {\vphantom {{\left\{ {{{({{q}_{0}} - q)} \mathord{\left/ {\vphantom {{({{q}_{0}} - q)} {\left[ {\left. {{{q}_{0}} - q\sum\limits_j {{{\alpha }_{j}}{{A}_{j}}} } \right)} \right]}}} \right. \kern-0em} {\left[ {\left. {{{q}_{0}} - q\sum\limits_j {{{\alpha }_{j}}{{A}_{j}}} } \right)} \right]}}} \right\}} q}} \right. \kern-0em} q},$

(8)

$\sum\limits_j {{{\alpha }_{j}}{{A}_{{j\infty }}}} \to {{{{q}_{0}}} \mathord{\left/ {\vphantom {{{{q}_{0}}} q}} \right. \kern-0em} q}\,\,{\text{при}}\,\,t \to \infty ,$

где A_j∞ – стационарная концентрация реагента A_j. Подставим (7) и (8) в каждое из решений (5) и исключим из них время

(9)

${{A}_{k}} = {{F}_{k}}\left( {\ln {{\left\{ {{{\left( {{{q}_{0}} - q} \right)} \mathord{\left/ {\vphantom {{\left( {{{q}_{0}} - q} \right)} {\left[ {\left. {{{q}_{0}} - q\sum\limits_j {{{\alpha }_{j}}{{A}_{j}}} } \right)} \right]}}} \right. \kern-0em} {\left[ {\left. {{{q}_{0}} - q\sum\limits_j {{{\alpha }_{j}}{{A}_{j}}} } \right)} \right]}}} \right\}} \mathord{\left/ {\vphantom {{\left\{ {{{\left( {{{q}_{0}} - q} \right)} \mathord{\left/ {\vphantom {{\left( {{{q}_{0}} - q} \right)} {\left[ {\left. {{{q}_{0}} - q\sum\limits_j {{{\alpha }_{j}}{{A}_{j}}} } \right)} \right]}}} \right. \kern-0em} {\left[ {\left. {{{q}_{0}} - q\sum\limits_j {{{\alpha }_{j}}{{A}_{j}}} } \right)} \right]}}} \right\}} q}} \right. \kern-0em} q},q,{{k}_{{i*}}}} \right) + {{C}_{k}};\,\,\,\,k \in [1,\,\, \ldots ,n].$

Перепишем эти равенства в виде

(10)

${{K}_{k}} \equiv {{A}_{k}} - {{F}_{k}}\left( {{{\ln \left\{ {{{({{q}_{0}} - q)} \mathord{\left/ {\vphantom {{({{q}_{0}} - q)} {\left[ {\left. {{{q}_{0}} - q\sum\limits_j {{{\alpha }_{j}}{{A}_{j}}} } \right)} \right]}}} \right. \kern-0em} {\left[ {\left. {{{q}_{0}} - q\sum\limits_j {{{\alpha }_{j}}{{A}_{j}}} } \right)} \right]}}} \right\}} \mathord{\left/ {\vphantom {{\ln \left\{ {{{({{q}_{0}} - q)} \mathord{\left/ {\vphantom {{({{q}_{0}} - q)} {\left[ {\left. {{{q}_{0}} - q\sum\limits_j {{{\alpha }_{j}}{{A}_{j}}} } \right)} \right]}}} \right. \kern-0em} {\left[ {\left. {{{q}_{0}} - q\sum\limits_j {{{\alpha }_{j}}{{A}_{j}}} } \right)} \right]}}} \right\}} q}} \right. \kern-0em} q},q,{{k}_{{i*}}}} \right) = {{C}_{k}};\,\,\,\,k \in [1,\,\, \ldots ,n].$

Каждое из полученных соотношений автономно, так как не зависит от времени, а зависит только от концентраций реагентов, кинетических параметров реакции (включая скорость потока) и н.у. Следовательно, соотношения (10) представляют собой новый вид НКЗС, который может наблюдаться экспериментально в нелинейных (и тем более в линейных) реакциях с участием free-реагентов, скорость образования которых не зависит от других реагентов. Число таких НКЗС равно числу free-реагентов и не превышает n − 1.

Отметим, что для стадий с участием free-реагентов решается и обратная задача (ОЗ), причем однозначно, с максимальной точностью и без использования оптимизационных методов. Это следует из того, что в стационарных состояниях ОДУ (4) становятся линейными по константам скоростей стадий алгебраическими уравнениями

(11)

$\sum\limits_{i*} {({{a}_{{i*k}}} - {{a}_{{ - i*k}}}){{k}_{{i*}}}} = {{({{q}_{0}}{{A}_{{0k}}} - q{{A}_{{k\infty }}})} \mathord{\left/ {\vphantom {{({{q}_{0}}{{A}_{{0k}}} - q{{A}_{{k\infty }}})} {\prod\limits_{jk} {A_{{k\infty }}^{{ai*k}}} }}} \right. \kern-0em} {\prod\limits_{jk} {A_{{k\infty }}^{{ai*k}}} }},$

решение которых записывается точно. Эти соотношения основаны на стационарных значениях концентраций реагентов, найденных экспериментально с неустранимой ошибкой (погрешностью измерений). Поэтому следует считать, что формулы (11) обеспечивают максимально возможную точность определения значений констант скоростей стадий. Под максимально возможной точностью понимается то, что системы линейных уравнений (кроме переопределенных) всегда решаются точно, а системы нелинейных уравнений, как правило, могут быть решены только приближенно, причем даже приближенных решений может и не быть.

Рассмотрим примеры установления НКЗС и применения их для решения обратной задачи конкретных нелинейных реакций.

Пример 1. Бимолекулярная реакция с участием двух реагентов:

(1.1)

$2{{{\mathbf{A}}}_{1}} = 2{{{\mathbf{A}}}_{2}},$

в открытом изотермическом безградиентном реакторе описывается ОДУ вида (2):

(1.2)

$A{\text{'}} = - 2{{k}_{1}}{{A}^{2}} + {\text{ }}2{{k}_{{ - 1}}}{{B}^{2}} + {{q}_{0}}{{A}_{0}} - qA,$

(1.3)

$B{\text{'}} = 2{{k}_{1}}{{A}^{2}} - 2{{k}_{{ - 1}}}{{B}^{2}} + {{q}_{0}}{{B}_{0}} - qB,$

где A и B– концентрации реагентов A₁ и A₂ соответственно. Для реакции (1.1) условие (3) существования free-реагента A₁ выполняется при k₋₁ = 0 (i* = 1), так как при этом скорость его образования (расходования) не зависит от концентрации реагента A₂ и уравнение (1.2) принимает вид (4). Следовательно, если реакция (1.1) не обратима, то для нее можно найти НКЗС вида (10). Запишем для этой реакции соотношения (5) и (6):

(1.4)

${{A}_{0}} + {{B}_{0}} = 1.$

(1.5)

$A{\kern 1pt} '\,\, + B{\kern 1pt} ' = {{q}_{0}}({{A}_{0}} + {{B}_{0}}) - q(A + B).$

Заменим уравнение (1.3) эквивалентным уравнением (1.5) и получим новую систему из двух уравнений (1.2) и (1.5), эквивалентную исходной системе (1.2), (1.3). Первое уравнение этой системы при k₋₁ = 0 является частным случаем уравнения Рикатти и интегрируется точно [20]. Проинтегрируем уравнения (1.2) и (1.5) и получим соответственно

(1.6)

$A = {{\left\langle { - q + {\text{th}}\left\{ {{{Dt} \mathord{\left/ {\vphantom {{Dt} 2}} \right. \kern-0em} 2} + {{\ln \left[ {{{\left( {q + D + 4{{A}_{0}}{{k}_{1}}} \right)} \mathord{\left/ {\vphantom {{\left( {q + D + 4{{A}_{0}}{{k}_{1}}} \right)} {( - q + D - 4{{A}_{0}}{{k}_{1}})}}} \right. \kern-0em} {( - q + D - 4{{A}_{0}}{{k}_{1}})}}} \right]} \mathord{\left/ {\vphantom {{\ln \left[ {{{\left( {q + D + 4{{A}_{0}}{{k}_{1}}} \right)} \mathord{\left/ {\vphantom {{\left( {q + D + 4{{A}_{0}}{{k}_{1}}} \right)} {( - q + D - 4{{A}_{0}}{{k}_{1}})}}} \right. \kern-0em} {( - q + D - 4{{A}_{0}}{{k}_{1}})}}} \right]} 2}} \right. \kern-0em} 2}} \right\}D} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle { - q + {\text{th}}\left\{ {{{Dt} \mathord{\left/ {\vphantom {{Dt} 2}} \right. \kern-0em} 2} + {{\ln \left[ {{{\left( {q + D + 4{{A}_{0}}{{k}_{1}}} \right)} \mathord{\left/ {\vphantom {{\left( {q + D + 4{{A}_{0}}{{k}_{1}}} \right)} {( - q + D - 4{{A}_{0}}{{k}_{1}})}}} \right. \kern-0em} {( - q + D - 4{{A}_{0}}{{k}_{1}})}}} \right]} \mathord{\left/ {\vphantom {{\ln \left[ {{{\left( {q + D + 4{{A}_{0}}{{k}_{1}}} \right)} \mathord{\left/ {\vphantom {{\left( {q + D + 4{{A}_{0}}{{k}_{1}}} \right)} {( - q + D - 4{{A}_{0}}{{k}_{1}})}}} \right. \kern-0em} {( - q + D - 4{{A}_{0}}{{k}_{1}})}}} \right]} 2}} \right. \kern-0em} 2}} \right\}D} \right\rangle } {4{{k}_{1}},}}} \right. \kern-0em} {4{{k}_{1}},}}$

(1.7)

$q\left( {A + B} \right) = {{q}_{0}} + {\text{ }}(q - {{q}_{0}})\exp ( - qt),$

где D ≡ (8q₀A₀k₁ + q²)^1/2 ≠ q + 4A₀k₁. Это неравенство проверяется возведением в квадрат его обеих частей, откуда следует q₀ ≠ q + 2A₀k₁, что не может выполняться как равенство в общем случае. Выразим из (1.7) с учетом (1.4) время

(1.8)

$t = {{\ln \left\{ {{{({{q}_{0}} - q)} \mathord{\left/ {\vphantom {{({{q}_{0}} - q)} {\left[ {{{q}_{0}} - q\left( {A + B} \right)} \right]}}} \right. \kern-0em} {\left[ {{{q}_{0}} - q\left( {A + B} \right)} \right]}}} \right\}} \mathord{\left/ {\vphantom {{\ln \left\{ {{{({{q}_{0}} - q)} \mathord{\left/ {\vphantom {{({{q}_{0}} - q)} {\left[ {{{q}_{0}} - q\left( {A + B} \right)} \right]}}} \right. \kern-0em} {\left[ {{{q}_{0}} - q\left( {A + B} \right)} \right]}}} \right\}} q}} \right. \kern-0em} q}.$

Подставим (1.8) в (1.6) и получим точный НКЗС общего вида (10):

(1.9)

$K \equiv {\text{th}}\left\{ {{{Dt} \mathord{\left/ {\vphantom {{Dt} 2}} \right. \kern-0em} 2} + {{\ln \left[ {{{\left( {q + D + 4{{A}_{0}}{{k}_{1}}} \right)} \mathord{\left/ {\vphantom {{\left( {q + D + 4{{A}_{0}}{{k}_{1}}} \right)} {\left( { - q + D - 4{{A}_{0}}{{k}_{1}}} \right)}}} \right. \kern-0em} {\left( { - q + D - 4{{A}_{0}}{{k}_{1}}} \right)}}} \right]} \mathord{\left/ {\vphantom {{\ln \left[ {{{\left( {q + D + 4{{A}_{0}}{{k}_{1}}} \right)} \mathord{\left/ {\vphantom {{\left( {q + D + 4{{A}_{0}}{{k}_{1}}} \right)} {\left( { - q + D - 4{{A}_{0}}{{k}_{1}}} \right)}}} \right. \kern-0em} {\left( { - q + D - 4{{A}_{0}}{{k}_{1}}} \right)}}} \right]} 2}} \right. \kern-0em} 2}} \right\}D - 4{{k}_{1}}A{\text{ }} = q,$

где t = ln{(q₀ − q)/[q₀ − q(A + B)]}/q, D = (8q₀A₀k₁ + + q²)^1/2. Этот НКЗС не зависит от времени и может наблюдаться экспериментально, т.е. является физически реализуемым. Например, при k₁= 4, q₀ = 2, q = 1, A₀ = 1, B₀ = 0 НКЗС (1.9) принимает вид

(1.10)

$K \equiv {\text{th}}\left\{ {{{{{{65}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\ln (A + B - 2)} \mathord{\left/ {\vphantom {{{{{65}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\ln (A + B - 2)} 2}} \right. \kern-0em} 2} + {{\ln \left[ {{{({{{65}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + {\text{ }}16)} \mathord{\left/ {\vphantom {{({{{65}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + {\text{ }}16)} {({{{65}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} - 16)}}} \right. \kern-0em} {({{{65}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} - 16)}}} \right]} \mathord{\left/ {\vphantom {{\ln \left[ {{{({{{65}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + {\text{ }}16)} \mathord{\left/ {\vphantom {{({{{65}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + {\text{ }}16)} {({{{65}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} - 16)}}} \right. \kern-0em} {({{{65}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} - 16)}}} \right]} 2}} \right. \kern-0em} 2}} \right\}{{65}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} - 16A = 1.$

При других н.у., например, q₀ = 1/2, A₀ = 3/4, B₀ = 1/4 НКЗС (1.9) запишется

(1.11)

$K \equiv {\text{th}}\left\{ {{{{{{13}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\ln (A + B - 2)} \mathord{\left/ {\vphantom {{{{{13}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\ln (A + B - 2)} 2}} \right. \kern-0em} 2} + {{\ln \left[ {{{({{{13}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + 13)} \mathord{\left/ {\vphantom {{({{{13}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + 13)} {({{{13}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} - 13)}}} \right. \kern-0em} {({{{13}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} - 13)}}} \right]} \mathord{\left/ {\vphantom {{\ln \left[ {{{({{{13}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + 13)} \mathord{\left/ {\vphantom {{({{{13}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} + 13)} {({{{13}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} - 13)}}} \right. \kern-0em} {({{{13}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} - 13)}}} \right]} 2}} \right. \kern-0em} 2}} \right\}{{13}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} - 16A = 1.$

Графические иллюстрации зависимостей A(t), B(t) и НКЗС (1.10) и (1.11) приведены на рис. 1.

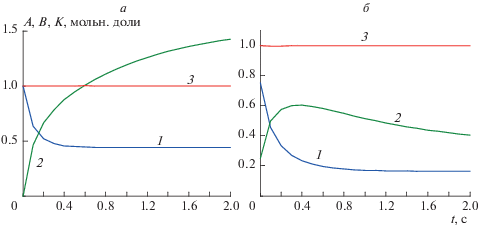
Рис. 1.

Зависимости: 1 − A(t), 2 − B(t) и 3 − K(t) для реакции (1.1) при k₁= 4 и н.у. q₀ = 2, q = 1, A₀ = 1, B₀ = 0 (а); q₀ = 1/2, A₀ = 3/4, B₀ = 1/4 (б).

Решим для реакции (1.1) ОЗ на основе стационарных данных. Проинтегрируем уравнения (1.2), (1.3) численно при любом заданном произвольно значении константы k₁, которое будем считать “истинным”, но неизвестным. Из рис. 1а видно, что, например при k₁ = 4, стационарная концентрация исходного реагента A_∞ ≈ 0.45 (ошибка – ∼5%). Точное значение, полученное при численных расчетах A_∞ ≈ 0.4414, т.е. ошибка (относительная) Δ ≈ (0.45 – 0.44)/0.45 ≈ 0.02 (2%). Уравнение (11) для этой реакции запишется 2k₁A² = = q₀A₀ − qA_∞, откуда при q₀ = 2, q = 1, A₀ = 1 находим k₁ = (q₀A₀ − qA_∞)/$\left( {{\text{2}}A_{\infty }^{2}} \right)$ ≈ 3.83. Отметим, что продукт этой реакции также можно считать free-реагентом (второго уровня), так как скорость его образования зависит только от его концентрации и концентрации другого (свободного) реагента. Это позволяет решить ОЗ и на основе стационарной концентрации реагента B_∞ ≈ 1.55 (см. рис. 1а). Так, из уравнения (1.3) в стационарном состоянии следует 2k₁A² + q₀B₀ − qB_∞= 0, откуда при B₀ = 0 получим k₁ ≈ 3.83. Как видно, результаты решения ОЗ близки к истинному значению k₁ = 4 с погрешностью (4 − 3.83)/4 = 0.0425 (4.25%), что сравнимо с типичными ошибками измерений порядка 5−10%.

Пример 2. Реакция A₁ = A₃, протекающая через три стадии:

(2.1)

${{{\mathbf{A}}}_{1}} = {{{\mathbf{A}}}_{2}},~\,\,\,\,{\mathbf{2}}{{{\mathbf{A}}}_{2}} = {\mathbf{2}}{{{\mathbf{A}}}_{3}},\,\,\,\,{{{\mathbf{A}}}_{3}} = {{{\mathbf{A}}}_{2}},$

в открытом изотермическом безградиентном реакторе описывается ОДУ:

(2.2)

$A{\kern 1pt} ' = - {{k}_{1}}A + {{k}_{{ - 1}}}{{B}^{2}} + {{q}_{0}}{{A}_{0}} - qA,$

(2.3)

$\begin{gathered} B{\kern 1pt} ' = {{k}_{1}}A - {{k}_{{ - 1}}}{{B}^{2}} - 2{{k}_{2}}{{B}^{2}} + {\text{ }}2{{k}_{{ - 2}}}{{C}^{2}} + {{k}_{3}}C - \\ - \,\,{{k}_{{ - 3}}}B + {{q}_{0}}{{B}_{0}} - qB, \\ \end{gathered} $

(2.4)

$C{\kern 1pt} ' = 2{{k}_{2}}{{B}^{2}} - 2{{k}_{{ - 2}}}{{C}^{2}} - {{k}_{3}}C + {{k}_{{ - 3}}}B + {{q}_{0}}{{C}_{0}} - qC,$

где A, B и С – концентрации реагентов A₁, A₂ и A₃ соответственно. Для схемы (2.1) условие существования free-реагента А₁ (3) запишется k₋₁ = 0 (i* = 1), так как при этом скорость его образования (расходования) не зависит от концентраций других реагентов и уравнение (2.2) принимает вид (4). Следовательно, если реакция (2.1) необратима, то для нее с помощью соотношений (4)−(9) можно найти НКЗС вида (10). В этом случае соотношения (5) и (6) принимают соответственно вид

(2.5)

${{A}_{0}} + {{B}_{0}} + {{С}_{0}} = {\text{ }}1,$

(2.6)

$A{\kern 1pt} '\,\, + B{\kern 1pt} '\,\, + C{\kern 1pt} ' = {{q}_{0}} - q(A + B + C).$

Заменим уравнение (2.3) эквивалентным уравнением (2.6). Проинтегрируем уравнения (2.2) и (2.6) и с учетом (2.5) получим

(2.7)

$\begin{gathered} \left( {{{k}_{1}} + q} \right)A = {{q}_{0}}{{A}_{0}} + \\ + \,\,(q - {{q}_{0}} + {{k}_{1}}){{A}_{0}}\exp \left[ { - \left( {{{k}_{1}} + q} \right)t} \right], \\ \end{gathered} $

(2.8)

$q(A + B + С) = {{q}_{0}} + (q - {{q}_{0}})\exp ( - qt).$

Из (2.8) следует

(2.9)

$\begin{gathered} \exp \left[ { - \left( {{{k}_{1}} + q} \right)t} \right] = {{\left[ {{\text{exp}}( - qt)} \right]}^{{{{\left( {{{k}_{1}} + q} \right)} \mathord{\left/ {\vphantom {{\left( {{{k}_{1}} + q} \right)} q}} \right. \kern-0em} q}~}}} = \\ = {{\left\{ {{{\left[ {q(A + B + С) - {{q}_{0}}} \right]} \mathord{\left/ {\vphantom {{\left[ {q(A + B + С) - {{q}_{0}}} \right]} {(q - {{q}_{0}})}}} \right. \kern-0em} {(q - {{q}_{0}})}}} \right\}}^{{{{\left( {{{k}_{1}} + q} \right)} \mathord{\left/ {\vphantom {{\left( {{{k}_{1}} + q} \right)} q}} \right. \kern-0em} q}}}}. \\ \end{gathered} $

Подставим (2.9) в (2.7) и найдем точный НКЗС общего вида (10):

(2.10)

$\begin{gathered} K \equiv \left( {{{k}_{1}} + q} \right)A - (q - {{q}_{0}} + {{k}_{1}}){{A}_{0}} \times \\ \times \,\,{{\left\{ {{{\left[ {q(A + B + С) - {{q}_{0}}} \right]} \mathord{\left/ {\vphantom {{\left[ {q(A + B + С) - {{q}_{0}}} \right]} {\left( {q - {{q}_{0}}} \right)}}} \right. \kern-0em} {\left( {q - {{q}_{0}}} \right)}}} \right\}}^{{{{\left( {{{k}_{1}} + q} \right)} \mathord{\left/ {\vphantom {{\left( {{{k}_{1}} + q} \right)} q}} \right. \kern-0em} q}}}} = {{q}_{0}}{{A}_{0}}. \\ \end{gathered} $

Варьируя параметры этого выражения, получим серию частных НКЗС. Например, при k₁= 1, q₀ = = 1/2, q = 1 для н.у. A₀ = 1, B₀ = 0, С₀ = 0 найдем

(2.11)

$K \equiv 2A - {{3{{{\left[ {2(A + B + С) - 1} \right]}}^{2}}} \mathord{\left/ {\vphantom {{3{{{\left[ {2(A + B + С) - 1} \right]}}^{2}}} 2}} \right. \kern-0em} 2} = {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}.$

Графическая иллюстрация зависимостей A(t), B(t), C(t) и НКЗС (2.11) приведена на рис. 2.

Рис. 2.

Зависимости: 1 − A(t), 2 − B(t), 3 − C(t) и 4 − K(t) для реакции (2.1) при k₁= 1, q₀ = 1/2, q = 1, A₀ = 1, B₀ = 0, С₀ = 0.

Из рис. 2 видно, что стационарная концентрация исходного реагента A_∞ ≈ 0.25 (ошибка – ∼5%). Точное значение, полученное при численных расчетах A_∞ ≈ 0.2411, т.е. ошибка (относительная) Δ ≈ ≈ (0.25 – 0.24)/0.25 ≈ 0.04 (4%). Уравнение (11) запишется k₁A = q₀A₀ − qA_∞, откуда при q₀ = 1/2, q = 1, A₀ = 1 находим k₁ = (q₀A₀ − qA_∞)/A_∞ ≈ 1, что полностью совпадает с точным значением k₁. Отметим, что в этой реакции другие реагенты не являются свободными и константы скоростей остальных стадий с помощью НКЗС (2.11) не определяются.

Пример 3. Реакция H₂ + (1/2)O₂ = H₂O, протекающая по механизму

(3.1)

${{{\text{H}}}_{2}} = 2{\text{H}},\,\,\,\,{{{\text{O}}}_{2}} = 2{\text{O}}*,\,\,\,\,2{\text{H}}{\kern 1pt} *{\kern 1pt} {\kern 1pt} + {\text{O}}* = {{{\text{H}}}_{{\text{2}}}}{\text{O,}}$

в открытом изотермическом безградиентном реакторе с участием пяти реагентов описывается ОДУ

(3.2)

$A{\kern 1pt} ' = - {{k}_{1}}A + {{k}_{{ - 1}}}{{D}^{2}} + {{q}_{0}}{{A}_{0}} - qA,$

(3.3)

$B{\kern 1pt} ' = - {{k}_{2}}B + {{k}_{{ - 2}}}{{E}^{2}} + {{q}_{0}}{{B}_{0}} - qB,$

(3.4)

$C{\kern 1pt} ' = {{k}_{3}}{{D}^{2}}E - {{k}_{{ - 3}}}C + {{q}_{0}}{{C}_{0}} - qC,$

(3.5)

$\begin{gathered} D{\kern 1pt} ' = 2{{k}_{1}}A - 2{{k}_{{ - 1}}}{{D}^{2}} - \\ - \,\,2{{k}_{3}}{{D}^{2}}E + 2{{k}_{{ - 3}}}C + {{q}_{0}}{{D}_{0}} - qD, \\ \end{gathered} $

(3.6)

$\begin{gathered} E{\kern 1pt} ' = 2{{k}_{2}}B - 2{{k}_{{ - 2}}}{{E}^{2}} - \\ - \,\,{{k}_{3}}{{D}^{2}}E + {{k}_{{ - 3}}}C + {{q}_{0}}{{E}_{0}} - qE, \\ \end{gathered} $

где A = [H₂], B = [O₂], C = [H₂O], D = [H*], E = [O*] – концентрации реагентов. В механизме (3.1) каждое из исходных веществ может быть free-реагентом. При выполнении условий (3) только для стадии i* = 1 таким реагентом становится H₂. При выполнении условий (3) только для стадии i* = 2 таким реагентом становится O₂. При выполнении условий (3) для обеих этих стадий i* = {1, 2} free-реагентами являются оба исходных вещества и при k₋₁ = k₋₂ = 0 можно найти два НКЗС вида (10). Запишем соотношения (5) и (6), например, для последнего случая

(3.7)

$2{{A}_{0}} + 2{{B}_{0}} + 3{{С}_{0}} + {{D}_{0}} + {{E}_{0}} = 1.$

(3.8)

$\begin{gathered} 2A{\kern 1pt} '\,\, + 2B{\kern 1pt} '\,\, + 3C{\kern 1pt} '\,\, + D{\kern 1pt} '\,\, + E{\kern 1pt} ' = \\ = {{q}_{0}} - q(2A + 2B + 3С + D + E), \\ \end{gathered} $

где F ≡ 2A + 2B + 3С + D + E. Заменим уравнение (3.5) эквивалентным уравнением (3.8). Проинтегрируем уравнения (3.2), (3.3) и (3.8) и получим соответственно

(3.9)

$\begin{gathered} \left( {{{k}_{1}} + q} \right)A = {{q}_{0}}{{A}_{0}} + \\ + \,\,(q - {{q}_{0}} + {{k}_{1}}){{A}_{0}}\exp \left[ { - \left( {{{k}_{1}} + q} \right)t} \right], \\ \end{gathered} $

(3.10)

$\begin{gathered} \left( {{{k}_{2}} + q} \right)B = {{q}_{0}}{{B}_{0}} + \\ + \,\,(q - {{q}_{0}} + {{k}_{2}}){{B}_{0}}\exp \left[ { - \left( {{{k}_{2}} + q} \right)t} \right], \\ \end{gathered} $

(3.11)

$qF = {{q}_{0}} + (q - {{q}_{0}})\exp ( - qt).$

Из (3.11) следует

(3.12)

$\begin{gathered} \exp \left[ { - \left( {{{k}_{1}} + q} \right)t} \right] = {{\left[ {\exp ( - qt)} \right]}^{{{{\left( {{{k}_{1}}\, + \,q} \right)} \mathord{\left/ {\vphantom {{\left( {{{k}_{1}}\, + \,q} \right)} q}} \right. \kern-0em} q}}}} = \\ = {{\left. {{{(qF - {{q}_{0}})} \mathord{\left/ {\vphantom {{(qF - {{q}_{0}})} {(q - {{q}_{0}})}}} \right. \kern-0em} {(q - {{q}_{0}})}}} \right\}}^{{{{\left( {{{k}_{1}}{\text{ }} + \,q} \right)} \mathord{\left/ {\vphantom {{\left( {{{k}_{1}}{\text{ }} + \,q} \right)} q}} \right. \kern-0em} q}}}}. \\ \end{gathered} $

Подставим (3.12) в (3.9), (3.10) и найдем два точных НКЗС общего вида

(3.13)

$\begin{gathered} {{K}_{A}} \equiv \left( {{{k}_{1}} + q} \right)A - (q - {{q}_{0}} + {{k}_{1}}){{A}_{0}} \times \\ \times \,\,{{\left[ {{{(qF - {{q}_{0}})} \mathord{\left/ {\vphantom {{(qF - {{q}_{0}})} {(q - {{q}_{0}})}}} \right. \kern-0em} {(q - {{q}_{0}})}}} \right]}^{{{{\left( {{{k}_{1}} + q} \right)} \mathord{\left/ {\vphantom {{\left( {{{k}_{1}} + q} \right)} q}} \right. \kern-0em} q}}}} = {{q}_{0}}{{A}_{0}}. \\ \end{gathered} $

(3.14)

$\begin{gathered} {{K}_{B}} \equiv \left( {{{k}_{2}} + q} \right)B - (q - {{q}_{0}} + {{k}_{2}}){{B}_{0}} \times \\ \times \,\,{{\left[ {{{(qF - {{q}_{0}})} \mathord{\left/ {\vphantom {{(qF - {{q}_{0}})} {(q - {{q}_{0}})}}} \right. \kern-0em} {(q - {{q}_{0}})}}} \right]}^{{{{\left( {{{k}_{2}} + q} \right)} \mathord{\left/ {\vphantom {{\left( {{{k}_{2}} + q} \right)} q}} \right. \kern-0em} q}}}} = {{q}_{0}}{{B}_{0}}. \\ \end{gathered} $

Например, при k₁= k₂= 1, q₀ = 1/2, q = 1, A₀ = 1/3, B₀ = 1/6, С₀ = D₀ = E₀ = 0 получим

(3.15)

$\begin{gathered} {{K}_{A}} \equiv 2A - \left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)\left( {{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}} \right) \times \\ \times \,\,{{\left[ {{{\left( {2A + 2B + 3С + D + E - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right)} \mathord{\left/ {\vphantom {{\left( {2A + 2B + 3С + D + E - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right)} {\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right)}}} \right. \kern-0em} {\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right)}}} \right]}^{2}} = {1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}. \\ \end{gathered} $

(3.16)

$\begin{gathered} {{K}_{B}} \equiv 2B - \left( {{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}} \right)\left( {{1 \mathord{\left/ {\vphantom {1 6}} \right. \kern-0em} 6}} \right) \times \\ \times \,\,{{\left[ {{{\left( {2A\, + \,2B + 3С + D + E - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right)} \mathord{\left/ {\vphantom {{\left( {2A\, + \,2B + 3С + D + E - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right)} {\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right)}}} \right. \kern-0em} {\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}} \right)}}} \right]}^{2}} = {1 \mathord{\left/ {\vphantom {1 {12}}} \right. \kern-0em} {12}}. \\ \end{gathered} $

Графические иллюстрации НКЗС (3.15) и (3.16) приведены на рис. 3.

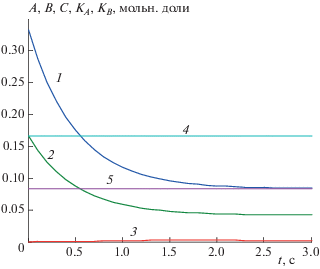
Рис. 3.

Зависимости: 1 − A(t), 2 − B(t), 3 − C(t), 4 − K_А(t), 5 − K_В(t) для реакции (3.1) при k₁= k₂= 1, q₀ = 1/2, q = 1, A₀ = = 1/3, B₀ = 1/6, С₀ = D₀ = E₀ = 0.

Решим ОЗ, измеряя стационарные концентрации двух free-реагентов A_∞ ≈ 0.08, B_∞ ≈ 0.04, см. рис. 3. Уравнения (11) (их здесь два) соответственно запишутся k₁A_∞ = q₀A₀ − qA_∞, k₂B_∞ = q₀B₀ − qB_∞. Отсюда при q₀ = 1/2, q = 1, A₀ = 1/3 находим k₁ ≈ ≈ 1.08, k₂ ≈ 1.08, что близко к точным значениям k₁ = k₂= 1 с погрешностью (1.08 − 1)/1 = 0.08 (8%).

ЗАКЛЮЧЕНИЕ

Разработан метод определения новых точных нелинейных кинетических законов сохранения (НКЗС), которые зависят от кинетических параметров и начальных условий проведения нелинейных реакций, протекающих в открытом изотермическом безградиентном реакторе. Механизмы таких реакций включают стадии превращения исходных веществ и не содержат стадий их образования, что характерно для большинства химических реакций. Динамика таких реакций описывается полиномиальными дифференциальными уравнениями, которые допускают точные решения и позволяют найти точные НКЗС. Полученные НКЗС расширяют представления о взаимосвязи механизмов с нестационарными характеристиками химических реакций и дополняют известные линейные стехиометрические и кинетические законы сохранения.

Автор выражает благодарность В.Х. Федотову за обсуждение работы.

Список литературы

Корзухин М.Д. Линейные законы сохранения в химической кинетике // Журн. физ. химии. 1972. Т. 46. № 7. С. 1845.
Горбань А.Н., Быков В.И., Яблонский Г.С. Очерки о химической релаксации. Новосибирск: Наука, 1986.
Алексеев Б.В., Кольцов Н.И., Федотов В.Х. // Журн. физ. химии. 1992. Т. 66. № 12. С. 3219.
Вольперт А.И., Худяев С.И. Анализ в классах разрывных функций и уравнения математической физики. М.: Наука, 1975.
Prelle M.J., Singer M.F. // Proc. 1981 ACM Symposium of Symbolic and Algebraic Computation. Snowbird, Utah (USA), 1981. P. 30.
Алексеев Б.В., Кольцов Н.И., Федотов В.Х. // Журн. физ. химии. 1988. Т. 62. № 11. С. 3069.
Кольцов Н.И. Математическое моделирование каталитических реакций. Чебоксары: Изд-во Чувашского ун-та, 2007.
Yablonsky G. S. // Theor. Found. of Chem. Eng. 2014. V. 48. № 5. P. 608.
Branco P.D., Yablonsky G.S., Marin G.B., Constales D. // Chem. Eng. Sci. 2017. V. 158. P. 370.
Peng B., Yablonsky G.S., Constales D., Marin G.B. // Ibid. 2018. V. 191. P. 262.
Branco P.D., Yablonsky G.S., Marin G.B., Constales D. // Ibid. V. 184. P. 25.
Yablonsky G.S., Branco P.D., Marin G.B., Constales D. // Ibid. 2019. V. 196. P. 384.
Федотов В.Х., Кольцов Н.И. // Хим. физика. 2019. Т. 38. № 4. С. 23.
Федотов В.Х., Кольцов Н.И. // Кинетика и катализ. 2019. Т. 60. № 6. С. 756; https://doi.org/10.1134/S0453881119060042
Федотов В.Х., Кольцов Н.И., Косьянов П.М. // Хим. физика. 2020. Т. 39. № 3. С. 48; https://doi.org/10.31857/S0207401X20030048
Кольцов Н.И. // Кинетика и катализ. 2020. Т. 61. № 4. С. 482.
Кольцов Н.И. // Теорет. основы хим. технологии. 2020. Т. 54. № 5. С. 592.
Кольцов Н.И. // Хим. физика. 2020. Т. 39. № 9. С. 23; https://doi.org/10.31857/S0207401X2009006X
Кольцов Н.И. // Кинетика и катализ. 2020. Т. 61. № 6. С. 783.
Степанов В.В. Курс дифференциальных уравнений. М.: URSS, 2016.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Химическая физика

Архивы выпусков Информация о журнале Отправить рукопись в журнал