1. На главную
  2. Электронные версии
  3. Химическая физика
  4. T. 42, № 7, 2023

Химическая физика, 2023, T. 42, № 7, стр. 70-77

Моделирование адсорбции водорода и кислорода на наночастицах палладия, расположенных на графитовой подложке с различными дефектами

Е. И. Руденко 1, *, Н. В. Дохликова 1, А. К. Гатин 1, С. Ю. Сарвадий 1, М. В. Гришин 1

1 Федеральный исследовательский центр химической физики им. Н.Н. Семёнова Российской академии наук,
Москва, Россия

* E-mail: rectedo@gmail.com

Поступила в редакцию 24.10.2022
После доработки 06.12.2022
Принята к публикации 20.12.2022

Полный текст (PDF)

Аннотация

С помощью моделирования в рамках теории функционала плотности адсорбции атомарных кислорода и водорода на поверхности наночастиц палладия на подложках графита с различными дефектами были рассчитаны энергии связи адатомов и изменения плотности состояний атомов металла при взаимодействии с адатомами. Установлено, что энергетическая стабильность адсорбции кислорода и водорода не зависит от места адсорбции адатома на поверхности наночастицы (интерфейс или вершина), что согласуется с результатами СТМ/СТС-экспериментов.

Ключевые слова: теория функционала плотности, наночастицы, палладий, кислород, водород, графит, адсорбция, квантовохимическое моделирование, сканирующая туннельная микроскопия, сканирующая туннельная спектроскопия.

1. ВВЕДЕНИЕ

Пленки из наночастиц металлов, нанесенные на химически инертные подложки, такие как графит или оксиды кремния, алюминия и другие [1, 2], являются наиболее применяемыми функциональными наноматериалами. С помощью варьирования элементного состава как структурированного на наноуровне покрытия, так и подложки [3, 4] можно добиться контролируемого изменения физико-химических свойств данных наноразмерных систем [5, 6]. Известно, что, несмотря на химическую инертность, подложки могут оказывать достаточно существенное влияние на многие характеристики наночастиц, такие как размеры, химический состав [7] и оптические свойства [8, 9]. Данная особенность может оказаться полезной, например, при создании элементов электроники с размером элементов <100 нм [10] и основы для разнообразных катализаторов [11, 12].

Наноразмерные структуры на основе палладия показали себя как перспективные функциональные наноматериалы. Многочисленные исследования доказали высокую каталитическую активность палладия в наноразмерных системах, в то время как в макромире при нормальных условиях палладий проявляет малую реакционную способность. Например, в обзоре [13] было показано, что наночастицы палладия являются перспективными катализаторами в реакциях образования С–С-связей, являющихся очень важными для химической промышленности. На наночастицах палладия также возможны некоторые электрохимические реакции, например электрокаталитическое восстановление углекислого газа, исследованное в работе [14] с помощью просвечивающей электронной микроскопии и квантовохимического моделирования в рамках теории функционала плотности (ТФП). В работе [15] с помощью ТФП исследован механизм окислительно-восстановительных реакций с участием кислорода и водорода на поверхности палладия (111). Помимо этого, также в рамках ТФП было проведено исследование наночастиц палладия на подложке CeO2 [16], где выявлено, что на интерфейсе образование интермедиата COOH многих органических реакций проходит быстрее и с бóльшим выходом. Было проведено ТФП-исследование замещенной и декорированной наночастицами палладия наноструктуры ZnO [17], которое показало сравнительно высокую чувствительность к газообразным водороду и этанолу. Кроме того, наночастицы палладия применяются в реакциях фоторазложения фенола [18], а также для покрытия углеродных нанотрубок при адсорбции газов в качестве катализатора [19].

В настоящее время многие вопросы в области исследований химической физики поверхности таких многокомпонентных систем, как нанесенные наночастицы металлов, в частности палладия, остаются открытыми по причине сложного совместного воздействия наночастиц и подложки друг на друга, а также на характеристики элементарных поверхностных реакций. Одним из возможных приближений, применяемых к таким системам, может быть разделение влияния подложки на атомную структуру наночастицы и на ее заряд вследствие разности энергий Ферми свободной наночастицы и подложки [20]. При этом электронное строение наночастиц благородных и переходных металлов представлено в рамках резонансной модели хемосорбции, т.е. модели центра d-зоны. Ранее этот подход зарекомендовал себя как разумное и достаточно точное приближение в области исследований поверхностной адсорбции [21].

Наиболее распространенным методом вычисления параметров нанесенных наночастиц металлов является моделирование в рамках ТФП, поскольку оно позволяет рассчитывать атомные структуры, включающие в себя до 100 атомов в ab initio приближении с разумными вычислительными затратами. Ранее в данном приближении уже были проведены исследования наночастиц золота, меди, никеля и платины [22–24]. Результаты моделирования коррелируют с результатами экспериментов, проведенных над этими, нанесенными на графит наночастицами с помощью методик сканирующей туннельной микроскопии и спектроскопии (СТМ/СТС) [25–28]. Совместное использование численного эксперимента с учетом квантовых эффектов и реального эксперимента с атомным разрешением впервые позволило установить взаимосвязь между изменением электронной структуры модели наночастицы и адсорбционными характеристиками реальной наночастицы, измеренными в СТМ/СТС-экспериментах.

В настоящей работе проводится исследование адсорбционных свойств нанесенных на графит наночастиц палладия на примере взаимодействия с атомарными кислородом и водородом с помощью квантовохимического моделирования в рамках ТФП. Результаты исследований будут сопоставлены как с экспериментальными данными, так и с результатами упомянутых выше работ.

2. МЕТОДИКА ИССЛЕДОВАНИЙ

Квантовохимическое моделирование наноразмерных систем, имитирующих наночастицы Pd, нанесенные на графитовую подложку с различными дефектами, проводилось в рамках теории функционала плотности с использованием пакетов с открытым программным кодом QuantumEspresso (QE) [29] и OpenMX (OMX) [30]. Для расчета электронной структуры использовано приближение LDA в ультрамягком псевдопотенциале с функционалом Пердью–Зингера и радиусом обрезания по энергии 39 Ry. Данные условия расчета были выбраны исходя из тестовых вычислений, которые показали лучшую сходимость по электронной подсистеме при выбранных параметрах. Наборы атомноцентрированных базисных функций взяты из документации к программному пакету OMX и примерно соответствовали базису на основе дубль-зета-орбиталей слетера.

Модель подложки представляла собой пластину (слаб) графита, состоящую из двух графеновых плоскостей, содержащих по 72 атома углерода. Площадь поверхности слáба составляла примерно 14 × 13 Å. Расстояние между плоскостями графена внутри слáба после оптимизации атомной структуры с варьированием параметров ячейки равно 4.34 Å. Величина вакуумного зазора составляла 14.5 Å. Тестовые расчеты показали, что при указанных размерах слáба подложки взаимное влияние нанесенных на нее кластеров палладия будет пренебрежимо мало.

В данном исследовании рассматривались следующие дефекты подложки: вакансия атома углерода, дефект поворота связи С–С (дефект 5/7 Стоуна–Уэльса), обрывы плоскости графена типа “зигзаг” и “кресло” (рис. 1). Во всех случаях атомная структура верхней плоскости графена, содержащая дефекты и обрывы, была дополнительно оптимизирована после основной оптимизации суперячейки слáба. Под оптимизацией атомной структуры подразумевается поиск координат атомов, при которых система, состоящая из этих атомов, имеет наименьшее значение энергии.

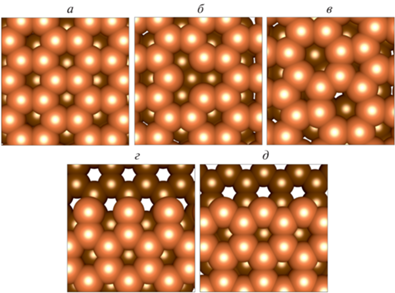
Рис. 1.

Атомная структура подложки графита: а – без дефектов, б – с вакансией, в – с дефектом поворота связи С–С, г – с обрывом плоскости графена типа “кресло”, д – с обрывом плоскости типа “зигзаг”.

В качестве исходной модели наночастиц Pd использовался 13-атомный икосаэдрический изомер кластера Pd13. Атомная структура кластеров рассчитывалась при фиксированном положении всех атомов подложки. Поскольку данная работа посвящена исследованию вопросов, касающихся выявления изменений электронной структуры адсорбционного комплекса под влиянием подложки, полученные наноразмерные системы Pd13-графит/графит с дефектами, соответствующие локальному энергетическому минимуму, удовлетворяют поставленным задачам.

Для каждой системы взаимодействие с адсорбатом, атомом водорода или кислорода, было рассчитано с оптимизацией положений атомов палладия и без таковой, т.е. положения атомов палладия были фиксированы. Сравнение величин энергий связи в этих двух случаях позволит оценить влияние подвижности атомов металла на энергию связи с адатомами. Для каждой системы проводилось моделирование двух положений атомов адсорбата (сайтов): в окрестности интерфейса кластер–графит s2 и на вершине кластера, вдали от интерфейса s1. На рис. 2 в качестве примера показаны сайты s1 (а) и s2 (б) адсорбции Н и сайты s1 (в) и s2 (г) адсорбции О кластера Pd13 на подложке графита без дефектов.

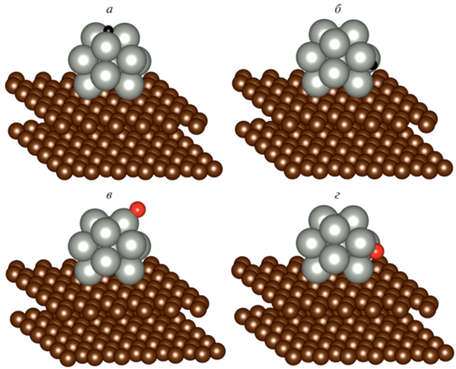
Рис. 2.

Примеры выбранных сайтов адсорбции атомов Н (а – s1, б – s2) и О (в – s1, г – s2) кластера Pd13 на подложке графита без дефектов.

Расчет изменения спроектированной плотности состояний отдельных атомов палладия вблизи сайта адсорбции адатомов является важной частью исследования, поскольку позволяет провести сопоставление результатов экспериментов с использованием методов СТМ/СТС и квантовохимического моделирования в рамках ТФП. Для получения более подробной информации отдельно изучено поведение s- и d-орбиталей атомов палладия. В предыдущих работах мы показали, что именно состояния атомов в окрестности уровня Ферми вносят основной вклад в изменение туннельного тока в СТС-спектроскопии [24, 25]. При небольших напряжениях смещения U туннельный ток I будет определяться только плотностью состояний образца:

(1)
$I(U) = {\text{const}} \cdot M{{\rho }_{{tip}}}(0)\int\limits_{ - eU}^0 {{{\rho }_{{sample}}}(\varepsilon )d\varepsilon } .$
Здесь M – усредненное значение матричного элемента перекрывания волновых функций зонда и атомов поверхности, ρtip(0) – аппроксимированное значение плотности состояний зонда вблизи уровня Ферми, ρsample(ε) – локальная плотность состояний образца, ε – собственные значения энергии.

3. РЕЗУЛЬТАТЫ

Предварительный расчет изменения плотности состояний атомов Pd свободного кластера Pd13 при взаимодействии с адатомами Н и О показал, что плотность состояний вблизи уровня Ферми образована в основном d-электронами, так же как и плотность состояний кластеров платины и никеля [24]. Отметим, что адсорбция O (рис. 3б) снижает плотность состояний сильнее, чем адсорбция H (рис. 3а). Энергии связи с атомом О больше энергии связи с атомом Н, что коррелирует с изменениями плотности состояний при взаимодействии с соответствующими адатомами (табл. 1).

Рис. 3.

Спроектированные плотности состояний адсорбционных комплексов О–Pd13 (а) и Н–Pd13 (б) и их конфигурационные диаграммы – справа; спроектированные плотности состояний d-орбиталей (толстая линия) и s-орбиталей (тонкая линия) атомов Pd; сплошная линия – до адсорбции, штриховая линия – после адсорбции атомов О (а) и Н (б).

Таблица 1.  

Величины энергий связи (в эВ) атомов Н и О со свободными кластерами Pd13

Адсорбат Энергия связи
H –3.27
O –4.02

Моделирование влияния графитовой подложки показало, что атомная структура кластера Pd13 претерпевает достаточно большую трансформацию только в системах с обрывами плоскостей графена типа “кресло” и “зигзаг”, после которой кластер теряет первоначальную икосаэдрическую симметрию. Этот эффект вполне очевиден, так как энергия связи между кластерами Pd13 и подложками с обрывами плоскостей графена – самая большая среди ряда благородных и переходных металлов (табл. 2). Однако при этом энергия связи кластера Pd13 с подложками без дефектов и с единичными дефектами меньше энергии связи кластера Ni13 и сопоставима с энергией связи кластера Pt13. Как уже отмечалось в предыдущих работах, для кластеров Ni13 и Au13 большее воздействие оказывает обрыв плоскости типа “зигзаг”. На кластер Pd13 большее влияние оказывает обрыв плоскости типа “кресло”, так же как и на кластеры Cu13 и Pt13 [22–24].

Таблица 2.  

Величины энергии связи (Есв, эВ) 13-атомных кластеров Cu13, Au13, Ni13, Pt13, Pd13 с подложками графита без дефекта (1), с вакансией (2), с дефектом Стоуна–Уэльса (3), обрыв плоскости графена типа “кресло” (4), обрыв плоскости графена типа “зигзаг” (5)

Кластер Eсв Заряд
1 2 3 4 5
Cu13 –0.17 –0.39 –0.19 –1.31 –1.01 +
Au13 –0.16 –0.42 –0.18 –1.60 –1.76 –
Ni13 –0.51 –0.90 –0.51 –1.97 –2.18 –
Pt13 –0.36 –0.53 –0.44 –2.78 –1.94 –
Pd13 –0.37 –0.46 –0.39 –2.86 –2.13 +

Анализ заселенности по Малликену и построение распределений электронной плотности системы Pd13–графит показали накопление положительного заряда на подсистеме металла. Моделирование адсорбции атомов H на поверхности кластеров Pd13 на различных подложках c единичными дефектами показало, что величины энергий связи вблизи интерфейса и на вершине различаются слабо (<0.1 эВ). Аналогичное моделирование адсорбции атомов O показало различие величин энергий связи до 0.8 эВ (табл. 3). Это обусловлено тем, что атом Н стабильно связывается с кластером Pd в положении над тремя атомами (трехцентровой сайт адсорбции), в то время как сайт адсорбции O может быть как трех-, так и двухцентровым (рис. 2, 4, 5). В целом энергия связи атома H для кластеров на подложках больше энергии связи атома Н со свободным кластером. Определенной зависимости для атома О не выявлено (табл. 1). Однозначного влияния дефектности подложки на энергию адсорбции не обнаружено, однако в системах с обрывами плоскости графита сильная трансформация кластера приводит к появлению сайтов с меньшей энергией связи. Включение подвижности атомов Pd в системах с обрывами плоскости графита также, очевидно, усиливает этот эффект. В остальном существенного влияния подвижности атомов Pd на величину энергии связи с адатомами не установлено.

Таблица 3.  

Энергия связи для сайтов адсорбции атомов H и О на кластерах Pd13 на подложках графита без дефекта (1), с вакансией (2), с дефектом 5/7 (3), обрыв плоскости графена типа “кресло” (4), обрыв плоскости графена типа “зигзаг” (5) при фиксированном (Eсв, эВ) и нефиксированном ($Е_{{{\mathbf{св}}}}^{{\mathbf{*}}}{\mathbf{,}}$ эВ) положениях атомов Pd (ΔEфикс = Eсв – $Е_{{{\mathbf{св}}}}^{{\mathbf{*}}}{\mathbf{,}}$ ΔEs = Eсв(s1) – Eсв(s2), ${\mathbf{\Delta }}Е_{s}^{*}$ = $Е_{{{\mathbf{св}}}}^{{\mathbf{*}}}$(s1) – $Е_{{{\mathbf{св}}}}^{{\mathbf{*}}}$(s2), эВ)

Адсорбат Подложка Eсв $Е_{{{\text{св}}}}^{*}$ ΔEфикс Eсв $Е_{{{\text{св}}}}^{*}$ ΔEфикс ΔEs $\Delta Е_{s}^{*}$
s1 s2
H  1 –4.24 –4.28 –0.03 –4.28 –4.33 –0.05 0.04 0.05
2 –4.32 –4.33 –0.01 –4.27 –4.30 –0.02 –0.05 –0.03
3 –4.23 –4.28 –0.04 –4.28 –4.30 –0.02 0.05 0.02
4 –4.11 –3.36 0.75 –3.92 –3.36 0.55 –0.19 0
5 –3.69 –4.57 –0.88 –3.79 –4.12 –0.33 0.1 –0.45
О 1 –3.48 –3.55 –0.06 –4.43 –4.65 –0.22 0.95 1.1
2 –5.01 –4.66 0.35 –4.44 –4.67 –0.24 –0.57 0.01
3 –4.58 –4.64 –0.07 –3.89 –4.69 –0.80 –0.69 0.05
4 –3.89 –4.52 –0.30 –4.23 –3.69 –1.02 0.34 –0.83
5 –4.08 –4.53 –0.44 –3.08 –4.38 –1.30 –1 –0.15
Рис. 4.

Спроектированные плотности состояний d-орбиталей (толстая линия) и s-орбиталей (тонкая линия) атомов Pd; сплошная линия – до адсорбции, штриховая – после адсорбции атомов Н на различных подложках: а и б – бездефектный графит, в и г – графит с вакансией, д и е – графит с дефектом 5/7, ж и з – обрыв плоскости графена типа “кресло”, к и л – обрыв плоскости графена типа “зигзаг”; для каждого адсорбционного комплекса на подложке представлены два сайта: слева – s1 на вершине, справа – s2 на интерфейсе. На вставке приведены атомные структуры кластеров Pd13 на подложке графита (вид сверху). Атомы Pd, для которых рассчитывались спроектированные плотности состояний, отмечены крестиком.

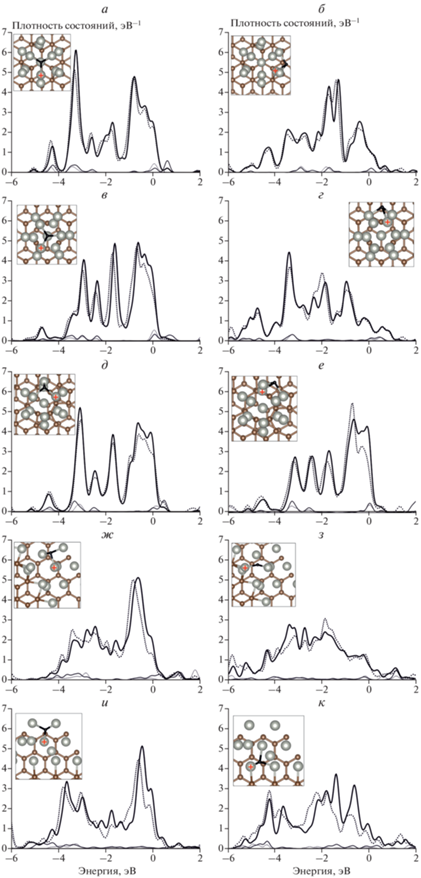
Рис. 5.

Спроектированные плотности состояний d-орбиталей (толстая линия) и s-орбиталей (тонкая линия) атомов Pd; сплошная линия – до адсорбции, штриховая – после адсорбции атомов О на различных подложках: а и б – бездефектный графит, в и г – графит с вакансией, д и е – графит с дефектом 5/7, ж и з – обрыв плоскости графена типа “кресло”, к и л – обрыв плоскости графена типа “зигзаг”; для каждого адсорбционного комплекса на подложке представлены два сайта: слева – s1 на вершине, справа – s2 на интерфейсе. На вставке приведены атомные структуры кластеров Pd13 на подложке графита (вид сверху). Атомы Pd, для которых рассчитывались спроектированные плотности состояний, отмечены крестиком.

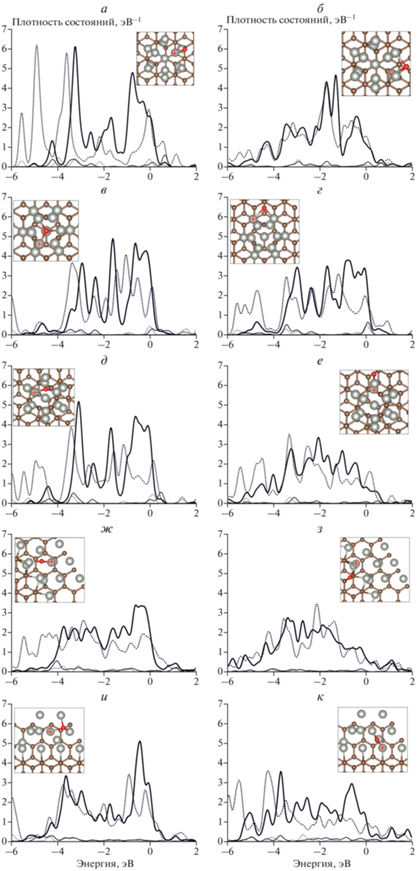
На рис. 4 и 5 приведены рассчитанные спроектированные плотности состояний s- и d-орбиталей атомов Pd сайтов адсорбции атомов H и О в системах с различными подложками. Расчет показал, что для каждой системы характерно снижение плотности состояний атомов Pd сайтов вблизи интерфейса, взаимодействующих с подложкой (рис. 4 б, г, е, з, к и 5 б, г, е, з, к). Однако вблизи уровня Ферми по-прежнему расположена “зона” d-орбиталей, как и в свободных 13-атомных кластерах (рис. 3).

Качественное изменение плотности состояний при взаимодействии с атомами Н и О атомов кластера Pd13 на подложке такое же, как и у свободного кластера Pd13. Снижение плотности состояний больше зависит от локального строения поверхности кластера, а не от расположения сайта адсорбции относительно подложки [22]. Можно отметить, что существенно увеличивается только энергия связи с атомом Н; для атома О какой-либо общей тенденции нет. Очевидно, что отсутствие единой тенденции энергии связи атома О объясняется появлением как двух-, так и трехцентровых сайтов адсорбции. При этом единообразие трехцентровых сайтов адсорбции атома Н делает заметным и преобладающим сильное взаимодействие кластера Pd13 с подложкой графита.

Полученные результаты соответствуют экспериментальным данным, согласно которым восстановление окисленных наночастиц палладия происходило одновременно как на интерфейсе с подложкой, так и на вершине. Проведенные расчеты показали, что каких-либо тенденций относительно энергий связи и изменения электронной структуры сайтов адсорбции атомов О и Н на кластере Pd13, указывающих на то, что адсорбция О и Н с большей вероятностью будет происходит на интерфейсе или на вершине, не обнаружено. Несмотря на некоторое сходство в адсорбционных свойствах и в электронном строении наночастицы палладия заметно отличаются от наночастиц никеля и платины, исследованных ранее.

4. ЗАКЛЮЧЕНИЕ

В результате ТФП-моделирования адсорбции Н и О на наночастицах в системе Pd13–графит установлено, что энергия связи адатомов Н с кластером Pd13 на подложках графита больше, чем со свободным кластером Pd13. Сайты адсорбции адатома О обладают большей вариативностью по атомной структуре и количеству центров, что приводит к большему разбросу по величинам энергии связи. Можно предположить, что влияние заряда кластера в системе Pd13–графит мaлó и более существенное воздействие на адсорбционные свойства последнего оказывает его атомная трансформация. Расчет энергий связи и изменений плотности состояний сайтов адсорбции Н и О не показал, где взаимодействие указанных адатомов более энергетически стабильно – на интерфейсе или на вершине. Данные моделирования коррелируют с результатами СТМ/СТС-экспериментов.

Все расчеты выполнены с использованием вычислительных ресурсов Межведомственного суперкомпьютерного центра РАН (МСЦ РАН).

Работа выполнена в рамках госзадания ФИЦ ХФ РАН (тема № 122040500058-1).

Список литературы

  1. Востриков А.А., Федяева А.Н., Фадеева О.Н. и др. // Сверхкритич. флюиды. Теория и практика. 2010. Т. 5. № 1. С. 12.

  2. Николаев А.Ю., Сизов В.Е., Абрамчук С.С. и др. // Сверхкритич. флюиды. Теория и практика. 2019. Т. 14. № 2. С. 105.

  3. Molodtsova O.V., Aristova I.M., Potorochin D.V. et al. // Appl. Surf. Sci. 2020. V. 506. P. 8.

  4. Magnin Y., Villermaux E., Amara H. et al. // Carbon. 2020. V. 159. P. 504.

  5. Хохлов С.С., Ходос И.И., Дьячкова Л.Г. и др. // Хим. физика. 2019. Т. 38. № 11. С. 34.

  6. Чернышева К.Ф., Ревина А.А // Хим. физика. 2019. Т. 38. № 5. С. 17.

  7. Molodtsova O.V., Aristova I.M., Potorochin D.V. et al. // Appl. Surf. Sci. 2020. V. 506. P. 8.

  8. Nevruzoglu V., Altuntas D.B., Tomakin M. // Appl. Phys. A. 2020. V. 126. № 4. P. 9.

  9. Журавлева Т.С., Иванова О.П., Криничная Е.П. и др. // Хим. физика. 2011. Т. 30. № 8. С. 75.

  10. Choi H., Nguyen P.T., Tran P.V. et al. // Appl. Surf. Sci. 2020. V. 510. P. 6.

  11. Bhaduri B., Polubesova V. // Mat. Lett. 2020. V. 267. P. 4.

  12. Ракитин М.Ю., Долуда В.Ю., Тянина А.А. и др. // Сверхкритич. флюиды. Теория и практика. 2016. Т. 11. № 3. С. 10.

  13. Balanta A., Godard C., Claver C. // Chem. Soc. Rev. 2011. V. 40. P. 4973

  14. Gao D., Zhou H., Wang J. et al. // J. Amer. Chem. Soc. 2015. V. 137. №. 13. P. 4288.

  15. Ou L., Chen S. // J. Phys. Chem. C. 2013. V. 117. P. 1342.

  16. Song W., Su Y.-Q., Hensen E.J.M. et al. // J. Phys. Chem. C. 2015. V. 119. № 49. P. 27505.

  17. Liangruksa M., Sukpoonprom P., Junkaew A. et al. // Appl. Surf. Sci. 2021. V. 544. P. 148868

  18. Su R., Tiruvalam R., He Q. et al. // Amer. Chem. Soc. 2012. V. 6. № 7. P. 6284.

  19. Cui H., Zhang X., Chen D. et al. // Appl. Surf. Sci. 2019. V. 471. P. 335.

  20. Николаевич Н.Н. // Технология конструкционных материалов. Анализ поверхности методами атомной физики. М.: “Юрайт”, 2018.

  21. Hammer B., Norskov J.K. // Surf. Sci. 1996. V. 359.

  22. Дохликова Н. В., Гатин А.К., Сарвадий С.Ю. и др. // Хим. физика. 2021. Т. 40. № 7. С. 67.

  23. Дохликова Н.В., Гатин А.К., Сарвадий С.Ю. и др. // Хим. физика. 2022. Т. 41. № 7. С. 76.

  24. Дохликова Н.В., Озерин С.А., Доронин С.В. и др. // Хим. физика. 2022. Т. 41. № 6. С. 72.

  25. Дохликова Н.В., Колченко Н.Н., Гришин М.В. и др. // Рос. нанотехнологии. 2016. Т. 11. № 11–12. С. 54.

  26. Гатин А.К., Сарвадий С.Ю., Дохликова Н.В. и др. // Хим. физика. 2021. Т. 40. № 6. С. 3.

  27. Гришин М.В., Гатин А.К., Дохликова Н.В. и др. // Хим. физика. 2019. Т. 38. № 1. С.3.

  28. Гатин А.К., Гришин М.В., Сарвадий С.Ю. и др. // Кинетика и катализ. 2018. Т. 59. № 2. С. 224.

  29. Giannozzi P., Andreussi O., Brumme T. et al. // J. Phys.: Condens. Matter. 2017. V. 29. № 46. P. 30.

  30. Ozaki T., Kino H. // Phys. Rev. B. 2004. V. 69. № 19. P. 19.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Химическая физика

Архивы выпусков Информация о журнале Отправить рукопись в журнал