Химия твердого топлива, 2021, № 6, стр. 41-49

ВВЕДЕНИЕ

Искусственные графиты широко используются как высокотемпературный конструкционный материал, с близкой к металлам проводимостью, в электротермических промышленных агрегатах. Для расчетов работы электротермических аппаратов используется температурная зависимость УЭС – важнейшее свойство искусственного графита. Ее анализ является актуальным объектом исследования с середины XX века [1, 2] и по настоящее время [3, 4]. Искусственный графит – это поликристалл, который получают с помощью нагрева заготовок на основе кокса до температур, обеспечивающих трехмерное упорядочение или графитацию. Упаковка кристалликов в искусственном графите определяется структурой исходного кокса. Кристаллики (структурные элементы) в поликристалле представляют собой подобные чешуйкам природного графита ламели, но в дальнейшем будем называть их графитовыми чешуйками.

Особенностью температурной зависимости УЭС искусственного графита является наличие характерного минимума при температуре около 700 K. Величина УЭС и ее температурная зависимость зависят от проводимостей чешуек графита параллельно и перпендикулярно графитовой плоскости, размеров и характера подключения чешуек в поликристалле [5, 6]. Особенности подключения чешуек включают сечения пятен контактов между чешуйками, расположение контактов на чешуйках и ориентацию чешуек. Для расчета величины УЭС предложена цепочечная модель, основанная на учете электрических подключений чешуек вдоль линий электрического тока в поликристалле.

В настоящей работе рассмотрены особенности математического расчета величины и температурной зависимости УЭС в приближении цепочечной модели с двухмерным распределением тока и унимодальностью чешуек для возможности оценки коэффициентов. Сравнение результатов математического моделирования проведено в виде численного расчета применительно к конструкционному графиту марки ГМЗ на основе изотропного кокса КНПС. Коэффициенты цепочечной модели связаны с такими параметрами кристаллической структуры, как размеры блоков мозаики, а также сечения пятен контактов и анизометрия чешуек. Эти параметры характеризуют структуру искусственного графита и ее изменение под действием внешних факторов, таких как нагрев, действие химически активной среды или радиация [7, 8], поэтому важно получение математической формулы для точного численного расчета величины и температурной зависимости УЭС на основе учитывающей пластинчатую структуру искусственного графита цепочечной модели.

Цепочечная модель. В работе [9] была получена следующая теоретическая формула для УЭС поликристаллического графита:

где $\rho {\text{*}}$ – УЭС поликристаллического графита, ${{\rho }_{a}}$ – УЭС чешуек параллельно графитовой плоскости, ${{\rho }_{c}}$ – УЭС чешуек перпендикулярно графитовой плоскости, $D$ – эффективный средний размер чешуек, $H$ – эффективная средняя толщина чешуек, ${{\varepsilon }}$ – эффективный линейный размер электрических контактов между чешуйками, $\nu = D{\text{/}}H$ – анизометрия чешуек, $\eta = {{\rho }_{a}}{\text{/}}{{\rho }_{c}}$ – анизотропия чешуек, ${{P}_{3}}$ – доля чешуек, подключенных по противоположным сторонам оснований, $p$ – количество цепочек, проходящих через единицу площади сечения.

Однако данная формула является грубой. Результаты физического моделирования [5] свидетельствуют о том, что слагаемое $\frac{{{{\rho }_{a}}}}{{(D - \varepsilon )H \cdot p}} \cdot 1$ при температурах, меньших 300 K, должно отсутствовать, иначе теоретическое магнетосопротивление получается слишком большим, поэтому в работе [10] с помощью более аккуратных аппроксимаций была получена новая формула

где $\chi (\mu ) = \frac{1}{2}\left( {1 + \tanh \left( {\frac{1}{{2.6\mu }} - 1.1{{\mu }^{2}}} \right)} \right)$ – срезающая функция, $K$ – коэффициент на текстуру, $S(\varepsilon )$ – коэффициент на плотность.

Здесь произведение коэффициентов $K \cdot S(\varepsilon )$ на текстуру и плотность формально равно $\frac{1}{{(D - \varepsilon )H \cdot p}}$. Однако на самом деле значение коэффициентов $K$ и $S(\varepsilon )$ гораздо сложнее оценить, поскольку зачастую имеются сложные дефекты, связанные с растрескиванием в области контактов чешуек, их неправильной формой, наложением проводящих цепочек друг на друга. Также трехмерное растекание тока около пятна контакта заменяется двумерным, что также требует своего поправочного коэффициента. Однако для дальнейших целей достаточно заменить влияние всех перечисленных факторов одним коэффициентом.

В следующих разделах исследована применимость формулы (6) для моделирования УЭС конструкционного графита марки ГМЗ. Опишем поликристаллический графит с помощью цепочечной модели.

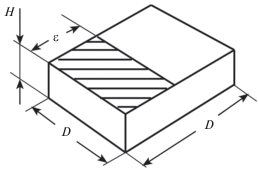
Представим пластинчатый поликристалл графита в виде множества проводящих цепочек. Звеньями этих цепочек будем считать графитовые чешуйки в форме параллелепипедов (рис. 1).

Соотношение $\varepsilon {\text{/}}D$ (ε – длина контакта, $D$ – длина всей чешуйки) может быть различным. Размер двух контактов на одной грани менее половины ее площади, в двумерном случае $\varepsilon {\text{/}}D < 1{\text{/}}2$, но с учетом неправильной формы чешуек верхней границей $\varepsilon {\text{/}}D$ фактически является $1{\text{/}}3$.

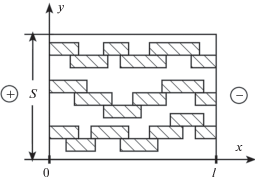
Выделим два основных вида подключения: подключение контактов по одну сторону основания 1–2 и подключение по противоположным сторонам оснований 1–3 (рис. 2).

Пусть ${{P}_{{3.}}}$ – вероятность того, что случайно взятая чешуйка имеет подключения по противоположным сторонам оснований. Иначе говоря, это доля чешуек в материале, подключенных с протеканием электрического тока наискосок от направления слоев. Будем считать, что в пластинчатом поликристалле их доля достаточно мала, порядка 10–30%.

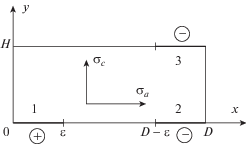
Для того чтобы теоретически оценить удельное электрическое сопротивление такого материала, брали образец длины $l$ и поперечным сечением площади $S$, который в разрезе изображен на рис. 3.

Тогда его электрическое сопротивление

где ${{\bar {R}}_{1}}$ – эффективное среднее сопротивление одной цепочки, $N$ – количество цепочек, ${{\bar {r}}_{{{\text{зв}}}}}$ – среднее сопротивление одной чешуйки, ${{\bar {n}}_{{{\text{зв}}}}}$ – среднее количество графитовых чешуек в одной цепочке, $p$ – количество цепочек, проходящих через единицу площади сечения.

Из формул (2) и $R = l \cdot \rho {\text{*/}}S$ следует формула для УЭС поликристалла графита вдоль оси x:

Здесь среднее сопротивление одной чешуйки ${{\bar {r}}_{{{\text{зв}}}}} = (1 - {{P}_{3}}) \cdot {{r}_{{{\text{зв}}1}}} + {{P}_{3}} \cdot {{r}_{{{\text{зв}}2}}}$, где ${{r}_{{{\text{зв}}1}}}$ – электрическое сопротивление чешуйки при подключении с одной стороны, ${{r}_{{{\text{зв2}}}}}$ – электрическое сопротивление чешуйки при подключении наискосок.

Для того чтобы вычислить сопротивление чешуйки, подключенной с одной стороны (см. рис. 2), электрический потенциал ${{\varphi }}(x,y)$ можно приближенно смоделировать с помощью решения следующей краевой задачи:

где ${{\sigma }_{a}} = 1{\text{/}}{{\rho }_{a}}$ – проводимость чешуйки параллельно графитовой плоскости, ${{\sigma }_{c}} = 1{\text{/}}{{\rho }_{c}}$ – проводимость чешуйки перпендикулярно графитовой плоскости, H – толщина чешуйки, D – длина и ширина чешуйки (рис. 1, 2).

Отметим, что допущение того, что нормальная составляющая плотности тока на поверхности контактов постоянна, нередко успешно применяется в моделировании, например в [11].

Аналогично, в случае подключения контактов наискосок, потенциал моделируется следующим образом:

С использованием метода Фурье в [10] было вычислено электрическое сопротивление ${{r}_{{{\text{зв}}1}}}$ одной чешуйки, с контактами 1 и 2, электрический потенциал которой описывается краевой задачей (4). В той же работе было вычислено электрическое сопротивление ${{r}_{{{\text{зв}}2}}}$ для чешуйки с контактами 1 и 3, электрический потенциал которой описывается задачей (5). После подстановки выражения ${{\bar {r}}_{{{\text{зв}}}}} = (1 - {{P}_{3}}) \cdot {{r}_{{{\text{зв}}1}}} + {{P}_{3}} \cdot {{r}_{{{\text{зв}}2}}}$ в (2) и математической аппроксимации рядов [10] получаем формулу (1). Тем самым, закончено описание цепочечной модели.

Проверка формулы (1). Сравнение с УЭС ГМЗ. Для проверки формулы (1) использовали данные (табл. 1) удельного электрического сопротивления для искусственного графита марки ГМЗ параллельно оси текстуры [12].

Теоретическую зависимость удельного электрического сопротивления построили с помощью формулы (1). В качестве значений УЭС чешуек графита параллельно и перпендикулярно графитовой плоскости использовали величины сопротивлений, данных для отоженного пирографита (табл. 2) с пересчетом на размер блоков мозаики, полученный из температуры минимума УЭС.

Поправку на размер блоков вычислили с помощью формулы Маттисена [13, 14]. Клейн [15] это правило использует в виде

где ${{l}_{p}}$ и ${{l}_{b}}$ – длина свободного пробега при рассеянии носителей заряда на фононах и на границах мозаики, а $C$ – некоторый коэффициент пропорциональности.

Для отожженного пирографита (квазимонокристалла) считали, что ${{l}_{b}}$ равно 2 мкм. В то же время известно (см. [16, 17]), что при температуре 300 K для графита длина свободного пробега электронов при рассеянии на фононах составляет ${{l}_{p}}$ = = 0.07 мкм. Согласно табл. 2, ${{\rho }_{a}}$  = 0.6 Ом мкм при 300 К, поэтому $C\,({{0.07}^{{ - 1}}} + {{2}^{{ - 1}}}) = 0.6$, откуда $C = 0.04\;Ом\,мк{{м}^{2}}$.

Длина свободного пробега при рассеянии носителей заряда на фононах ${{l}_{p}}$ является величиной, зависящей от температуры. На основании данных табл. 2 можно считать, что для УЭС вдоль слоев $l_{p}^{{ - 1}} = kT$, где $k$ – некоторый коэффициент. Поскольку на каждые 100 K УЭС увеличивается на 0.1 Ом мкм, то $k \cdot C = 0.001$ Ом мкм K^–1. Следовательно, $k = 0.025\;мк{{м}^{{ - 1}}}\,{{K}^{{ - 1}}}$. Итак,

Для графита ГМЗ можно с помощью формулы Кинчина [1] оценить ${{l}_{b}}$ по температуре минимума УЭС, равной (согласно табл. 1) ${{T}_{{\min }}}$ = 700 K. Таким образом, для графита ГМЗ ${{l}_{b}} = \frac{a}{{T_{{\min }}^{2}}} \approx 150$ нм = = 0.15 мкм, где $a = 7 \cdot {{10}^{7}}$ нм ${{K}^{2}}$ [18, 6 (с. 143)]. Данная величина вполне соответствует материалу на основе кокса КНПС, величина ${{l}_{b}}$ для которого составляет 127 нм (данные работы [5]).

Таким образом, для кристалликов ГМЗ получаем

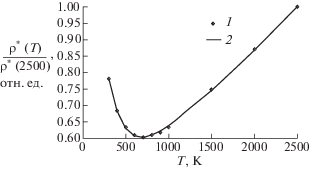
т.е. величина поправки равна Выберем параметры, используемые в теоретической формуле (1). На рис. 4 изображен график температурной зависимости УЭС графита марки ГМЗ и теоретической температурной зависимости УЭС поликристалла графита при ${{P}_{3}} = 0.25$, ${{\nu }} = 26.2$, $\varepsilon {\text{/}}D = 1{\text{/}}4$.

Заметим, что данные значения являются не единственными, другие подходящие значения приведены в табл. 3.

Таким образом, при увеличении ${{P}_{3}}$ от 0 до 1 подходящая анизометрия ${{\nu }}$ возрастает от 21 до 36.5, а относительная площадь пятна контакта ${{\varepsilon /}}D$ снижается от 1/4.7 до 1/2.7.

Из этих результатов можно сделать вывод о том, что теоретическая температурная зависимость УЭС поликристалла графита, вычисленная по формуле (1), при таких параметрах может быть согласована с экспериментальными значениями (табл. 1). На абсолютную величину УЭС также влияет пористость искусственного графита, входящая в коэффициент $K \cdot S(\varepsilon )$, и которая легко может быть изменена операцией уплотнения. Однако пористость не меняет положения минимума, поэтому использованы относительные величины УЭС.

Таким образом, формула (1) позволяет добиться прямого соответствия вычисленных значений УЭС экспериментальным результатам. Заметим, что максимальная относительная погрешность теоретического описания формулой (1) табличных данных ГМЗ не превосходит 2.9%. Отметим также, что для соответствия экспериментальной кривой подходят целые серии теоретических параметров микроструктуры.

Оценка параметров микроструктуры по температурной зависимости УЭС поликристалла графита. Используя табл. 1 температурной зависимости УЭС графита, можно приближенно определить значения поправочного коэффициента $K \cdot S(\varepsilon )$, произведений ${{\nu }^{{ - 1}}}\ln \frac{D}{\varepsilon }$ и ${{\nu }^{{ - 2}}}{{P}_{3}}$. Для этого составим систему уравнений из четырех уравнений, используя формулу (1):

Здесь с помощью ${{\rho }_{a}}(T)$, ${{\rho }_{c}}(T)$, $\rho {\kern 1pt} *(T)$ обозначаются УЭС чешуек параллельно графитовой плоскости, УЭС чешуек перпендикулярно графитовой плоскости и УЭС поликристалла графита при некоторой температуре T, ${{\eta }^{{ - 0.5}}}(T) = \sqrt {\frac{{{{\rho }_{c}}(T)}}{{{{\rho }_{a}}(T)}}} $, χ(μ) = = $\frac{1}{2}\left( {1 + \operatorname{th} \left( {\frac{1}{{2.6}} - 1.1{{\mu }^{2}}} \right)} \right)$. Отметим, что срезающая функция $\chi = 0$ при $T = 300$ K и $\chi = 1$ при $T = 1500$ K.

Используя значения $\rho {\text{*}}(300) = 9.6$, $\rho {\kern 1pt} *(700)$ = = 7.4, $\rho {\kern 1pt} *(1500) = 9.2$ из табл. 1 и значения ${{\rho }_{a}}(300) = 0.85$, ${{\rho }_{a}}(700) = 1.25$, ${{\rho }_{a}}(1500) = 2.05$, ${{\rho }_{с}}(300) = 2100$, ${{\rho }_{с}}(700) = 850$, ${{\rho }_{с}}(1500) = 180$ из табл. 2, из системы (7) можно определить значения $K \cdot S(\varepsilon )$, ${{\nu }^{{ - 1}}}$, $\ln \frac{D}{\varepsilon }$ и ${{P}_{3}}$. Однако система (7) в силу нелинейности и слабой определенности сложна для решения даже численными методами, поэтому ее желательно упростить. Например, выше методом подбора было установлено, что при $\nu = 26.2$ наблюдается хорошее соответствие между теоретической температурной зависимостью УЭС поликристалла и значениями УЭС искусственного графита марки ГМЗ вдоль оси текстуры. Подставив в систему (7) значение анизометрии $\nu = 26.2$ и используя первые три ее уравнения, можно вычислить

Вычислим также оценку поправочного коэффициента $K$на текстуру по аналогии с работой Рейнольдса [19]. Пусть $0 \leqslant \theta \leqslant \pi {\text{/}}2$ – угол между плоскостью чешуйки и основным направлением протеканию тока через поликристалл. Тогда $\rho {\kern 1pt} * = \frac{{{{\rho }_{{{\text{эф}}}}}}}{{\sin \theta }}$, где ${{\rho }_{{{\text{эф}}}}}$ – УЭС поликристалла в случае идеальной ориентации чешуек вдоль направления тока. Поправочный коэффициент $K$ на текстуру можно определить как математическое ожидание

где $\Gamma $ – поверхность верхней полусферы единичного радиуса, $I(\alpha ,{{\theta }})$ – плотность вероятности распределения положения чешуйки, определяемого с помощью углов $0 \leqslant \alpha \leqslant 2\pi $ и $0 \leqslant \theta \leqslant \pi {\text{/}}2$. В случае разориентации чешуек плотность распределения можно считать равномерной и равной $\frac{1}{{{{S}_{\Gamma }}}} = \frac{1}{{2\pi }}$, тогда

Поправка на плотность возникает из-за того, что проводящие чешуйки заполняют не весь объем поликристалла, а только его часть. При расчете поправки на плотность (пористость) будем считать, что

где ${{d}_{0}}$ – плотность чешуек, ${{d}_{k}}$ – плотность поликристалла графита. Плотность поликристалла графита ГМЗ ${{d}_{k}}$, согласно [12], составляет 1.6–1.72 г/$с{{м}^{3}}$. У монокристалла графита плотность ${{d}_{0}} = 2.24$ г/$с{{м}^{3}}$. Соответственно, поправка только на плотность $S(\varepsilon )$ составляет 1.3–1.4.

В результате получаем, что оценкой коэффициента $K \cdot S(\varepsilon )$ является значение, равное 2.04–2.2. Эта оценка совпадает по порядку с величиной коэффициента K ⋅ S(ε) = $\frac{{\rho {\text{*}}}}{{{{\rho }_{a}}\left( {\chi (\alpha ) + \alpha \cdot \ln \left( {\frac{D}{\varepsilon }} \right) + {{\alpha }^{2}} \cdot {{P}_{3}}} \right)}}$, где $\alpha = {{\nu }^{{ - 1}}}{{\eta }^{{ - 0.5}}}$ при некоторой температуре T, значение $\rho {\text{*}}$ взято из табл. 3 при температуре T, которая составляет 3–3.5. Расхождение этих оценок, возможно, объясняется грубостью модели и требует дополнительного рассмотрения.

Исследование влияния параметров микроструктуры на температурную зависимость УЭС поликристалла графита. Возьмем за основу значения параметров $\varepsilon {\text{/}}D = 0.25$, ${{P}_{3}} = 0.25$ и $\nu = 26.2$ и рассмотрим влияние каждого из них на УЭС по отдельности. Варьируя эти параметры, можно оценить возможные интервалы их изменения.

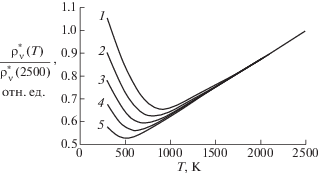
Как показано в [6, 20], значительной частью УЭС является контактное сопротивление. Непосредственное влияние на него оказывает эффективная ширина электрических контактов между чешуйками графита. На рис. 5 изображена теоретическая относительная температурная зависимость УЭС по отношению к УЭС графита при T = = 2500 K при изменении параметра $\varepsilon {\text{/}}D$. Отметим, что отношение $\varepsilon {\text{/}}D$ слабо влияет на положение минимума УЭС: минимумы всех линий 1–4 на рис. 5 примерно соответствуют экспериментальному значению минимума УЭС графита ГМЗ при 700 К.

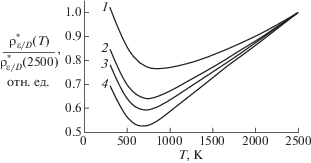
Как было замечено выше, в силу геометрии чешуек верхней границей параметра $\varepsilon {\text{/}}D$ можно считать 1/3. Нижняя граница может приближаться к нулю, однако можно заметить, что при $\varepsilon {\text{/}}D < 0.1$ характерный минимум УЭС поликристалла графита начинает сглаживаться и уходить в зону высоких температур.

Кроме сечения пятна контакта на УЭС оказывают влияние вероятность подключения чешуек и их эффективная анизометрия. На рис. 6 и 7 изображены относительные температурные зависимости УЭС при изменении этих параметров.

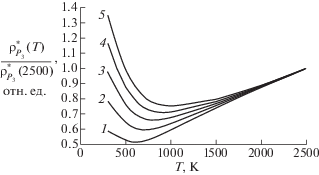
Как видно на рис. 6, изменение вероятности подключения изменяет наклон графита, сдвигает положение минимума, однако при любом его значении график УЭС имеет форму, характерную для УЭС поликристалла графита. Таким образом, с математической точки зрения вероятность ${{P}_{3}}$ может изменяться от 0 до 1, однако с физической точки зрения $0 < {{P}_{3}} < 0.33$.

Заметим, что относительно небольшое увеличение анизометрии значительно уменьшает УЭС и сдвигает температуру минимума в сторону более низких температур. По наблюдаемым характерным температурам минимума можно заключить, что анизометрия ${{\nu }}$ составляет величину порядка 16–40.

Наконец, в абсолютное значение УЭС свой вклад вносит коэффициент на текстуру и плотность $K \cdot S(\varepsilon )$, однако его изменение не приводит к изменению характера температурной зависимости УЭС и положения его минимума.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Температурная зависимость УЭС монокристалла графита в настоящее время хорошо изучена [21]. Однако УЭС поликристалла графита имеет более сложное поведение, а именно: УЭС имеет характерный минимум при температуре около 700 K. Интерпретация температурной зависимости УЭС поликристалла графита обычно дается с использованием качественной характеристики ее участков. При низкой температуре вид зависимости подобен наблюдаемой у полупроводников, и определяется энергией активации. При высокой температуре считается, что электрон-фононное взаимодействие определяет металлоподобный характер температурной зависимости. Положение минимума относят к переходной области.

Результаты использования цепочечной модели хорошо согласуются с экспериментальными данными несмотря на то, что вычисления проведены без учета температурного растрескивания [22–24]. Однако, по-видимому, растрескивание в искусственных графитах на основе порошка имеет меньшее влияние на УЭС, чем в модельной композиции на основе природного чешуйчатого графита [10]. Возможно, критическое значение для необходимости учета температурного растрескивания имеет средний размер чешуек.

В качестве направления дальнейших исследований цепочечной модели можно предложить теоретическое обоснование эмпирической формулы Кинчина ${{l}_{b}} = \frac{a}{{T_{{\min }}^{2}}}$ [1], так как ${{l}_{b}}$ влияет на УЭС в виде поправки к ${{\rho }_{a}}$ (12).

ВЫВОДЫ

Проведено исследование по соответствию УЭС графита ГМЗ и УЭС, рассчитанного по цепочечной модели. Показано, что ее четырех параметров ($K \cdot S(\varepsilon )$, $\varepsilon {\text{/}}D$, ${{P}_{3}}$ и ν) достаточно для моделирования УЭС графита ГМЗ на интервале температур 300–2500 K с относительной погрешностью, не превосходящей 2.9%. Улучшив оценку параметра $K \cdot S(\varepsilon )$, можно исключить его из “свободно изменяемых” параметров. Срезающая функция ${{\chi }}$ не является “параметром”, так как она была получена только из соображений математической аппроксимации сумм рядов и без изменений использована для другого материала [10].

Введение в цепочечную модель поправки на размер блоков мозаики по правилу Маттисена не только увеличило ее точность, но и может позволить теоретически обосновать зависимость среднего размера блоков и температуры минимума УЭС.