1. На главную
  2. Электронные версии
  3. Кинетика и катализ
  4. T. 61, № 4, 2020

Кинетика и катализ, 2020, T. 61, № 4, стр. 482-488

Точные автономные инварианты нелинейных химических реакций

Н. И. Кольцов *

ФГБОУ ВО Чувашский государственный университет им. И.Н. Ульянова, химико-фармацевтический факультет
428015 Чебоксары, Московский просп., 15, Россия

* E-mail: koltsovni@mail.ru

Поступила в редакцию 27.11.2019
После доработки 28.12.2019
Принята к публикации 30.12.2019

Полный текст (PDF)

Аннотация

Определены точные автономные (не зависящие от времени) кинетические инварианты нелинейных химических реакций, протекающих в открытых системах с участием одного независимого и любого числа зависимых реагентов. Такие инварианты представляют собой остающиеся постоянными в течение всей реакции соотношения, связывающие нестационарные значения концентраций реагентов, измеренных в нескольких экспериментах с разными начальными условиями (в мультиэкспериментах). Приведены примеры расчета инвариантов нелинейных реакций с двумя, тремя и четырьмя реагентами. Полученные результаты могут быть полезны при решении обратных задач нестационарной химической кинетики и моделировании процессов в изотермических реакторах идеального смешения.

Ключевые слова: нелинейные химические реакции, реактор идеального смешения, открытые системы, законы сохранения, инварианты

Поиск точных автономных (не зависящих от времени) инвариантов химических реакций является одной из интересных задач нестационарной химической кинетики. Инварианты представляют собой комбинации неравновесных концентраций реагентов, остающиеся постоянными в ходе реакции, т.е. выражают законы сохранения (ЗС) реагентов. Структура инвариантов может быть различной (линейные, нелинейные, стехиометрические, кинетические, моноэкспериментные и мультиэкспериментные). Законы сохранения на основе данных одного неравновесного эксперимента (моноинварианты) известны давно, и их исследовали М.Д. Корзухин (1972 г.), А.И. Вольперт и С.И. Худяев (1975 г.), M.J. Prelle и M.F. Singer (1981 г.), Г.С. Яблонский, В.И. Быков и А.Н. Горбань (1983 г.) и др. [1–6]. Законы сохранения на основе данных нескольких неравновесных экспериментов (мультиинварианты) обнаружены недавно (2010 г.), их активно исследуют G.S. Yablonsky, D. Constales и G.B. Marin с соавт. [7–18]. В настоящее время методом дуал-экспериментов (МДЭ) найдены точные МДЭ-инварианты линейных (многостадийных) и нелинейных (одно- и двухстадийных) реакций в закрытых системах. МДЭ основан на двух неравновесных экспериментах с взаимно-обратными граничными (“термодинамическими”) начальными условиями (н. у.). В работах [19–27] разработан более общий метод мультиэкспериментов (ММЭ), который допускает использование любого числа неравновесных экспериментов с любыми (не обязательно граничными) н. у. С его помощью найдены альтернативные ММЭ-инварианты линейных (многостадийных) реакций и нелинейных (одно-, двух- и трехстадийных) реакций с двумя реагентами (одним независимым) в закрытых системах. Отметим, что на практике расчет значений этих двух альтернативных типов инвариантов одинаково предполагает задание механизма реакции, но они отличаются по числу, структуре и области применения. Каждый механизм реакции характеризуется только одним МДЭ-ивариантом, который полностью определяется наблюдаемыми в дуал-эксперименте концентрациями всех реагентов, причем МДЭ-инварианты применимы только в закрытых системах. Число альтернативных ММЭ-инвариантов для каждого набора н. у. равно числу реагентов в механизме реакции, и эти инварианты выражаются через концентрации только одного (любого) реагента и (дополнительно) через константы скоростей всех стадий. Областью применения ММЭ-инвариантов являются как закрытые, так и открытые системы. Так, в работе [27] установлены ММЭ-инварианты линейных реакций в закрытых и открытых системах. Однако точные ММЭ-инварианты для многостадийных нелинейных реакций до сих пор не найдены. В связи с этим в данной статье была исследована возможность установления точных ММЭ-инвариантов многостадийных нелинейных реакций, протекающих с участием одного независимого и любого числа зависимых реагентов в открытых системах.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Пусть химическая реакция протекает нелинейно через стадии вида

(I)
$\begin{gathered} {{a}_{i}}{\mathbf{A}} + {{b}_{i}}{\mathbf{B}} + {{с}_{i}}{\mathbf{С}} + \ldots = {{a}_{{ - i}}}{\mathbf{A}} + {{b}_{{ - i}}}{\mathbf{B}} + {{с}_{{ - i}}}{\mathbf{С}} + \ldots , \\ i = 1, \ldots ,s, \\ \end{gathered} $
где a±i, b±i, c±i, … − стехиометрические коэффициенты реагентов А, В, С, … в стадии i, причем только один из этих реагентов (любой) независим. Динамика такой реакции в открытом изотермическом реакторе идеального смешения в рамках закона действующих масс описывается системой обыкновенных дифференциальных уравнений (ОДУ)
(1)
$A{\kern 1pt} ' = \sum {({{a}_{{ - i}}} - {{a}_{i}})({{r}_{i}} - {{r}_{{ - i}}})} {\text{ }} + q({{A}_{0}} - A),$
(2)
$B{\kern 1pt} ' = \sum {({{b}_{{ - i}}} - {{b}_{i}})({{r}_{i}} - {{r}_{{ - i}}})} + q({{B}_{0}} - B),$
(3)
$С{\kern 1pt} ' = \sum {({{с}_{{ - i}}} - {{с}_{i}})({{r}_{i}} - {{r}_{{ - i}}})} + q({{С}_{0}} - С),\,\, \ldots ,$
где ri = kiAaiBbiCci … и r−i = k−iAa −iBb −iCc − i … − скорости прямых и обратных стадий (1/с), A(t), B(t), C(t), … − текущие концентрации реагентов А, В, С, … (мол. доля), t − время (с), ki и k−i − константы скоростей стадий (1/с), q − скорость потока через реактор (1/с), A(0) = A0, B(0) = B0, C(0) = C0, … − концентрации реагентов на входе в реактор (н. у.). Стационарные состояния (с. с.) A∞, B∞, C∞, … определяются из условий
(4)
$A{\kern 1pt} ' = B{\kern 1pt} ' = C{\kern 1pt} ' = \ldots = 0.$
Если в реакции (I) существуют линейные законы сохранения (ЛЗС) вида
(5)
$\begin{gathered} {{\alpha }_{j}}A + {{\beta }_{j}}B + {{\gamma }_{j}}С + \ldots = {{\alpha }_{j}}{{A}_{\infty }} + {{\beta }_{j}}{{B}_{\infty }} + {{\gamma }_{j}}{{C}_{\infty }} + \ldots = \\ = {{\alpha }_{j}}{{A}_{0}} + {{\beta }_{j}}{{B}_{0}} + {{\gamma }_{j}}{{C}_{0}} + \ldots = {\text{Const}}, \\ \end{gathered} $
где αj, βj, γj, … − коэффициенты, зависящие от стехиометрии и констант скоростей стадий, то размерность системы (1)–(3) можно понизить на число таких ЛЗС. Как показано в [6], общее число ЛЗС вида (5) равно
(6)
$N = {{N}_{{\text{s}}}} + {{N}_{{\text{k}}}} = n - {{R}_{{\text{k}}}},$
где Ns = n − Rs − число стехиометрических ЛЗС, Nk = n − Rk − число кинетических ЛЗС, n – общее число реагентов (включая зависимые), Rs − ранг матрицы стехиометрических коэффициентов, Rk − ранг по комплексам (разным элементарным стадиям). Из (5) и (6) следует, что, если
(7)
$N = n - 1,$
то система (1)–(3) может быть сведена к одному эквивалентному ОДУ
(8)
$A{\kern 1pt} ' = f\left( {{\mathbf{a}},A\left( t \right)} \right),$
где f – полином степени max(a±i + b±i + c±i + …), a = a(ki, k−i, q, A0, B0, C0, …) – вектор параметров. Для бимолекулярных реакций это уравнение запишется
(9)
$A{\kern 1pt} ' = c{{A}^{2}} + aA + b.$
Общее решение уравнения (10) имеет вид
(10)
$\begin{gathered} A(t) = \\ = {{\left( { - a + D{\text{tg}}\left( {{{Dt} \mathord{\left/ {\vphantom {{Dt} 2}} \right. \kern-0em} 2} + {\text{arctg}}\left( {{{\left( {a + 2{{A}_{0}}c} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2{{A}_{0}}c} \right)} D}} \right. \kern-0em} D}} \right)} \right)} \right)} \mathord{\left/ {\vphantom {{\left( { - a + D{\text{tg}}\left( {{{Dt} \mathord{\left/ {\vphantom {{Dt} 2}} \right. \kern-0em} 2} + {\text{arctg}}\left( {{{\left( {a + 2{{A}_{0}}c} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2{{A}_{0}}c} \right)} D}} \right. \kern-0em} D}} \right)} \right)} \right)} {(2c)}}} \right. \kern-0em} {(2c)}}, \\ \end{gathered} $
где a(ki, k−i, q), b(ki, k−i, q, A0), c(ki, k−i) ≠ 0 – параметры, D = (4bc − a2)1/2. Единственное устойчивое с. с. A∞ = −(a + (−D)1/2)/(2с) физично при

(11)
$\begin{gathered} 0 \leqslant {{A}_{\infty }} \leqslant {\text{ }}1,\,\,\,\,c + a + b < 0, \\ {{a}^{2}} > 4bc,\,\,\,\,a < 0,\,\,\,\,b > 0. \\ \end{gathered} $

Применим ММЭ и запишем решение (10), (11) для любых двух н. у. A01 ≠ A02, отличных от с. с.

(12)
${{A}_{1}}\left( t \right) = {{\left[ { - a + {{D}_{1}}{\text{tg}}\left( {{{{{D}_{1}}t} \mathord{\left/ {\vphantom {{{{D}_{1}}t} 2}} \right. \kern-0em} 2} + {{z}_{{01}}}} \right)} \right]} \mathord{\left/ {\vphantom {{\left[ { - a + {{D}_{1}}{\text{tg}}\left( {{{{{D}_{1}}t} \mathord{\left/ {\vphantom {{{{D}_{1}}t} 2}} \right. \kern-0em} 2} + {{z}_{{01}}}} \right)} \right]} {\left( {2c} \right)}}} \right. \kern-0em} {\left( {2c} \right)}},$
(13)
${{A}_{2}}\left( t \right) = {{\left[ { - a + {{D}_{2}}{\text{tg}}\left( {{{{{D}_{2}}t} \mathord{\left/ {\vphantom {{{{D}_{2}}t} 2}} \right. \kern-0em} 2} + {{z}_{{02}}}} \right)} \right]} \mathord{\left/ {\vphantom {{\left[ { - a + {{D}_{2}}{\text{tg}}\left( {{{{{D}_{2}}t} \mathord{\left/ {\vphantom {{{{D}_{2}}t} 2}} \right. \kern-0em} 2} + {{z}_{{02}}}} \right)} \right]} {\left( {2c} \right)}}} \right. \kern-0em} {\left( {2c} \right)}},$
где z01 ≡ arctg((a + 2cA01)/D1), z02 ≡ arctg((a + 2cA02)/ D1), D1 ≡ (4b1c − a2)1/2, D2 ≡ (4b2c − a2)1/2, b1 = b(ki, k−i, q, A01), b2 = b(ki, k−i, q, A02). Исключим из (12), (13) время и получим ММЭ-инвариант по реагенту А (в тригонометрической форме):
(14)
${{K}_{A}}\left( t \right) \equiv {{({{D}_{2}}{{z}_{1}} - {{D}_{1}}{{z}_{2}})} \mathord{\left/ {\vphantom {{({{D}_{2}}{{z}_{1}} - {{D}_{1}}{{z}_{2}})} {({{D}_{2}}{{z}_{{01}}} - {{D}_{1}}{{z}_{{02}}})}}} \right. \kern-0em} {({{D}_{2}}{{z}_{{01}}} - {{D}_{1}}{{z}_{{02}}})}} = 1,$
где z1 ≡ arctg((a + 2cA1)/D1), z2 ≡ arctg((a + 2cA02)/D1). Этот инвариант не зависит от времени, является физичным и может наблюдаться экспериментально. Инварианты по остальным (зависимым) реагентам B, C, … совпадают по форме с (14) и находятся с помощью ЛЗС (5) соответствующими заменами A на В, А на С и т.д. Отметим, что инварианты вида (14) являются функциями комплексного аргумента, но принимают действительные значения и могут быть записаны в различных формах (логарифмической, степенной, экспоненциальной и др.). Инвариант (14) в логарифмической форме с учетом равенства [28] arctg(z) = −iln{[(1 + + is1)/(1 − is1)/2 запишется в виде
(15)
$\begin{gathered} {\text{ln}}{{K}_{A}}\left( t \right) \equiv \\ \equiv {\text{ln}}\left\{ {{{\left[ {{{\left( {1 + i{{s}_{1}}} \right)} \mathord{\left/ {\vphantom {{\left( {1 + i{{s}_{1}}} \right)} {{{{(1 - i{{s}_{1}})}}^{g}}}}} \right. \kern-0em} {{{{(1 - i{{s}_{1}})}}^{g}}}}} \right]} \mathord{\left/ {\vphantom {{\left[ {{{\left( {1 + i{{s}_{1}}} \right)} \mathord{\left/ {\vphantom {{\left( {1 + i{{s}_{1}}} \right)} {{{{(1 - i{{s}_{1}})}}^{g}}}}} \right. \kern-0em} {{{{(1 - i{{s}_{1}})}}^{g}}}}} \right]} {\left[ {{{\left( {1 + i{{s}_{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {1 + i{{s}_{2}}} \right)} {{{{(1 - i{{s}_{2}})}}^{f}}}}} \right. \kern-0em} {{{{(1 - i{{s}_{2}})}}^{f}}}}} \right]}}} \right. \kern-0em} {\left[ {{{\left( {1 + i{{s}_{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {1 + i{{s}_{2}}} \right)} {{{{(1 - i{{s}_{2}})}}^{f}}}}} \right. \kern-0em} {{{{(1 - i{{s}_{2}})}}^{f}}}}} \right]}}} \right\} = \\ = 0, \\ \end{gathered} $
где s1 ≡ (a + 2cA1)/D1, s2 ≡ (a + 2cA2)/D2, f ≡ −iD1/2, g ≡ −iD2/2. В закрытых системах в соотношениях (14) или (15) следует полагать q = 0, b1 = b2 и D1 = D2.

Для тримолекулярных реакций уравнение (8) запишется как

(16)
$A{\kern 1pt} ' = d{{A}^{3}} + c{{A}^{2}} + aA + b,$
где a(ki, k−i, q), b(ki, k−i, q, A0), c(ki, k−i), d(ki, k−i) ≠ 0 – параметры. Отсюда следует, что хотя бы одно физичное с. с. 0 ≤ A∞ ≤ 1 существует при условии
(17)
$A{\kern 1pt} '\left( 0 \right)A{\kern 1pt} '\left( 1 \right) = b(d + c + a + b) \leqslant 0.$
Общее решение уравнений (16), (17) можно записать в виде [29]:
(18)
$L\left( A \right) = {{L}_{0}} + t,$
где L(A) ≡ ln(A − A1∞)/s1 + ln(A − A2∞)/s2 + ln(A − − A3∞)/s3, L0 ≡ ln(A0 − A1∞)/s1 + ln(A0 − A2∞)/s2 + + ln(A0 − A3∞)/s3. Здесь s1 ≡ ${\text{3}}dA_{{1 \propto }}^{{\text{2}}}$ + 2cA1∞ + a, s2 ≡ ≡ ${\text{3}}dA_{{2 \propto }}^{2}$ + 2cA2∞ + a, s3 ≡ ${\text{3}}dA_{{{\text{3}} \propto }}^{{\text{2}}}$ + 2cA3∞ + a; A1∞, A2∞ и A3∞ − три с. с., включая нефизичные (комплексные).

Применим ММЭ и запишем решение (18) для любых двух н. у. (отличных от с. с.), исключим t и получим инвариант по реагенту А:

(19)
${{K}_{A}}\left( t \right) \equiv {{({{L}_{1}} - {{L}_{2}})} \mathord{\left/ {\vphantom {{({{L}_{1}} - {{L}_{2}})} {({{L}_{{01}}} - {{L}_{{02}}})}}} \right. \kern-0em} {({{L}_{{01}}} - {{L}_{{02}}})}} = 1,$
где L1 ≡ ln(A1 − A1∞1)/s11 + ln(A1 − A2∞1)/s21 + ln(A1 − − A3∞1)/s31, L2 ≡ ln(A2 − A1∞2)/s12 + ln(A2 − A2∞2)/ s22 + ln(A2 − A3∞2)/s32, L01 ≡ ln(A01 − A1∞1)/s11 + ln(A01 − − A2∞1)/s21 + ln(A01 − A3∞1)/s31, L02 ≡ ln(A02 − A1∞2)/ s12 + ln(A02 − A2∞2)/s22 + ln(A02 − A3∞2)/s32. Здесь s11 = ${\text{3}}dA_{{{\text{1}} \propto {\text{1}}}}^{{\text{2}}}$ + 2cA1∞1 + a, s21 = ${\text{3}}dA_{{2 \propto 1}}^{{\text{2}}}$ + 2cA2∞1 + a, s31 = ${\text{3}}dA_{{3 \propto 1}}^{2}$ + 2cA3∞1 + a – значения s1, s2 и s3 в первом эксперименте, s12, s22 и s32– значения s1, s2 и s3 во втором эксперименте, A1∞1, A2∞1 и A3∞1 − три с. с. в первом эксперименте, A1∞2, A2∞2 и A3∞2 − три с. с. во втором эксперименте. Инвариант (19) не зависит от времени, является физичным и может наблюдаться экспериментально. Инварианты по остальным (зависимым) реагентам B, C, … совпадают по форме с (19) и находятся с помощью ЛЗС (5) соответствующими заменами A на В, А на С и т.д. В закрытых системах в соотношениях (19) следует полагать q = 0, b1 = b2.

Применим полученные соотношения к конкретным нелинейным химическим реакциям, удовлетворяющим условию (8), т.е. протекающим с участием любого числа зависимых и одного независимого реагентов в открытых системах.

Пример 1. Бимолекулярная реакция

(II)
$2{\mathbf{A}} = 2{\mathbf{B}},$
в открытой системе описывается следующими уравнениями вида (1.1)–(1.3):
(2.1)
$A{\kern 1pt} ' = - 2{{k}_{1}}{{A}^{2}} + {\text{ }}2{{k}_{{ - 1}}}{{B}^{2}} + q({{A}_{0}} - A),$
(2.2)
$B{\kern 1pt} ' = 2{{k}_{1}}{{A}^{2}} - 2{{k}_{{ - 1}}}{{B}^{2}} + q({{B}_{0}} - B).$
В этой реакции участвуют два реагента А и В (n = 2) и два комплекса 2A и 2B. Из (6) находим Rs = 1, Rk = 1, N = 1, Ns = 1 и Nk = 0, т.е. выполняется условие (7), и есть только один ЛЗС A + B = 1, который позволяет понизить порядок системы (2.1)–(2.2) на единицу и заменить ее одним ОДУ вида (9):
(2.3)
$\begin{gathered} A{\kern 1pt} ' = - 2{{k}_{1}}{{A}^{2}} + 2{{k}_{{ - 1}}}{{(1 - A)}^{2}} + q({{A}_{0}} - A) \equiv \\ \equiv c{{A}^{2}} + aA + b, \\ \end{gathered} $
где с = 2(k−1 − k1) ≠ 0 при k1 ≠ k−1, a = −(4k−1 + q), b = 2k−1 + qA0. Условия физичности (11) выполняются, например, при k1= 4, k−1 = 1, q = 1. Тогда с учетом ЗС для первого граничного н. у. A01 = 1, B01 = 0 получим c = −6, a = −5, b1 = 3, D1 = −971/2, а для второго граничного н. у. A02 = 0, B02 = 1 получим b2 = 2, D2 = −731/2. Подставим эти значения в (14) и найдем A-инвариант
(2.4)
$\begin{gathered} {{K}_{A}}(t) \equiv \left[ {{{D}_{2}}{\text{arctg}}\left( {{{(5 + 12{{A}_{1}})} \mathord{\left/ {\vphantom {{(5 + 12{{A}_{1}})} {{{D}_{1}}}}} \right. \kern-0em} {{{D}_{1}}}}} \right) - } \right. \\ {{\left. { - \,\,{{D}_{1}}{\text{arctg}}\left( {{{(5 + 12{{A}_{2}})} \mathord{\left/ {\vphantom {{(5 + 12{{A}_{2}})} {{{D}_{2}}}}} \right. \kern-0em} {{{D}_{2}}}}} \right)} \right]} \mathord{\left/ {\vphantom {{\left. { - \,\,{{D}_{1}}{\text{arctg}}\left( {{{(5 + 12{{A}_{2}})} \mathord{\left/ {\vphantom {{(5 + 12{{A}_{2}})} {{{D}_{2}}}}} \right. \kern-0em} {{{D}_{2}}}}} \right)} \right]} {{{K}_{{A0}}}}}} \right. \kern-0em} {{{K}_{{A0}}}}} = 1, \\ \end{gathered} $
где KA0 ≡ D2arctg(17/D1) − D1arctg(17/D2). Для двух произвольных н. у. с учетом ЗС, например, A01 = 1, B01 = 0 получим c = −6, a = −5, b1 = 3, D1 = −971/2, A02 = 1/2, B02 = 1/2, b2 = 2.5, D2 = −851/2 и найдем новый А-инвариант, который отличается от (2.4) только значением D2 (рис. 1).

Рис. 1.

Концентрационные зависимости A1(t), A2(t) и A-инвариант (2.4) для реакции (II) при k1 = 4, k−1 = 1, q = 1 и н. у. A01 = 1, A02 = 1/2: 1 – A1(t), 2 – A2(t), 3 – KA(t).

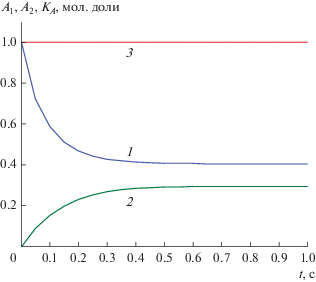
Как видно на рис. 1, инвариант KA(t) не зависит от времени и наблюдается экспериментально в виде горизонтальной линии. Инварианты по реагенту B находятся из (2.4) с учетом ЗС и заменами A1 = 1 − B1 и A2 = 1 − B2.

Пример 2. Двухстадийная реакция, протекающая по схеме

(III)
$1)\,\,{\mathbf{A}} = {\mathbf{B}},\,\,\,\,2)\,\,{\mathbf{2B}} = {\mathbf{2A}},$
в открытой системе описывается уравнениями вида (1)–(3):
(3.1)
$\begin{gathered} A{\kern 1pt} ' = - {{k}_{1}}A + {{k}_{{ - 1}}}B + 2{{k}_{2}}{{B}^{2}} - \\ - \,\,2{{k}_{{ - 2}}}{{A}^{2}} + q({{A}_{0}} - A), \\ \end{gathered} $
(3.2)
$B{\kern 1pt} ' = {{k}_{1}}A - {{k}_{{ - 1}}}B - 2{{k}_{2}}{{B}^{2}} + 2{{k}_{{ - 2}}}{{A}^{2}} + q({{B}_{0}} - B).$
В этой реакции участвуют два реагента (n = 2) и четыре комплекса А, В, 2A и 2B. Из (6) находим Rs = 1, Rk = 1, N = 1, Ns = 1 и Nk = 0, т.е. выполняется условие (7), и есть один ЛЗС A + B = 1, который позволяет понизить порядок системы (3.1)–(3.2) на единицу и заменить ее одним ОДУ вида (9):
(3.3)
$\begin{gathered} A{\kern 1pt} ' = - {{k}_{1}}A + {{k}_{{ - 1}}}(1 - A) + 2{{k}_{2}}{{(1 - A)}^{2}} - \\ - \,\,2{{k}_{{ - 2}}}{{A}^{2}} + q({{A}_{0}} - A), \\ \end{gathered} $
где c = 2(k2 − k−2) ≠ 0 при k2 ≠ k−2, a = −(k1 + k−1 + + 4k2 + q) < 0, b = k−1+ 2k2 + qA0 > 0. Условия физичности (11) реализуются, например, при k1= 4, k−1 = 1, k2 = 1, k−2 = 0.5, q = 1. Тогда a = −10, b1 = = 3 + A01, c = 1 и при н. у. A01 = 1 получим b1 = 4, D1 = −841/2, а при A02 = 1/2 получим b2 = 3.5, D2 = = −861/2. А-инвариант (14) для реакции (III) примет вид
(3.4)
$\begin{gathered} ~{{K}_{A}}(t) \equiv \left[ {{{D}_{2}}{\text{arctg}}\left( {{{(2{{A}_{1}} - 10)} \mathord{\left/ {\vphantom {{(2{{A}_{1}} - 10)} {{{D}_{1}}}}} \right. \kern-0em} {{{D}_{1}}}}} \right) - } \right. \\ {{\left. { - \,\,{{D}_{1}}{\text{arctg}}\left( {{{(2{{A}_{2}} - 10)} \mathord{\left/ {\vphantom {{(2{{A}_{2}} - 10)} {{{D}_{2}}}}} \right. \kern-0em} {{{D}_{2}}}}} \right)} \right]} \mathord{\left/ {\vphantom {{\left. { - \,\,{{D}_{1}}{\text{arctg}}\left( {{{(2{{A}_{2}} - 10)} \mathord{\left/ {\vphantom {{(2{{A}_{2}} - 10)} {{{D}_{2}}}}} \right. \kern-0em} {{{D}_{2}}}}} \right)} \right]} {{{K}_{{A0}}}}}} \right. \kern-0em} {{{K}_{{A0}}}}} = {\text{ }}1, \\ \end{gathered} $
где KA0 ≡ D2arctg(−8/D1) − D1arctg(−9)/D2). Инвариант (3.4) показан на рис. 2.

Рис. 2.

Концентрационные зависимости A1(t), A2(t) и А-инвариант (3.4) для реакции (III) при k1= 4, k−1 = 1, k2 = 1, k−2 = 0.5, q = 1 и н. у. A01 = 1, A02 = 1/2, B01 = 0, B02 = 1/2: 1 – A1(t), 2 – A2(t), 3 – KA(t).

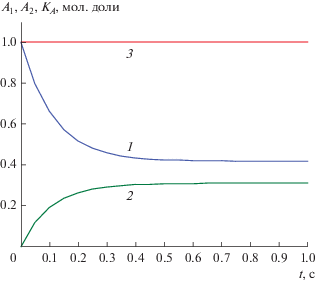
Как видно на рис. 2, KA(t) является точным инвариантом. Второй инвариант по реагенту B находится из (3.4) заменами A1 = 1 − B1 и A2 = 1 − B2.

Пример 3. Рассмотрим трехстадийную автокаталитическую реакцию

(IV)
$1)\,\,{\mathbf{A}} = {\mathbf{B}},\,\,\,\,2)\,\,2{\mathbf{B}} = 2{\mathbf{A}},\,\,\,\,3)\,\,{\mathbf{A}} + {\mathbf{B}} = 2{\mathbf{B}}.$
Динамика этой реакции в открытой системе описывается уравнениями:
(4.1)
$\begin{gathered} A{\kern 1pt} ' = - {{k}_{1}}A + {{k}_{{ - 1}}}B + 2{{k}_{2}}{{B}^{2}} - 2{{k}_{{ - 2}}}{{A}^{2}} - \\ - \,\,{{k}_{3}}AB + {{k}_{{ - 3}}}{{B}^{2}} + q({{A}_{0}} - A), \\ \end{gathered} $
(4.2)
$\begin{gathered} B{\kern 1pt} ' = {{k}_{1}}A - {{k}_{{ - 1}}}B - 2{{k}_{2}}{{B}^{2}} + 2{{k}_{{ - 2}}}{{A}^{2}} + \\ + \,\,{{k}_{3}}AB - {{k}_{{ - 3}}}{{B}^{2}} + q({{B}_{0}} - B). \\ \end{gathered} $
В этой реакции участвуют два реагента (n = 2) и пять комплексов А, В, 2A, 2B и (A + B). Из (6) находим Rs = 1, Rk = 1, N = 1, Ns = 1 и Nk = 0, т.е. выполняется условие (7), и есть один ЛЗС A + B = 1, который позволяет понизить порядок системы (4.1)–(4.2) и заменить ее одним ОДУ вида (9):
(4.3)
$\begin{gathered} A{\kern 1pt} ' = - {{k}_{1}}A + {{k}_{{ - 1}}}(1 - A) + 2{{k}_{2}}{{(1 - A)}^{2}} - 2{{k}_{{ - 2}}}{{A}^{2}} - \\ - \,\,{{k}_{3}}A(1 - A) + {{k}_{{ - 3}}}{{(1 - A)}^{2}} + q({{A}_{0}} - A), \\ \end{gathered} $
где c = 2(k2 − k−2) + k3 + k−3, a = −(k1 + k−1 + 4k2 + + k3 + 2k−3 + q) < 0, b = k−1+ 2k2 + k−3 + qA0 > 0. Условия физичности (11) реализуются, например, при k1= 4, k−1 = 1, k2 = 1, k−2 = 0.5, k3 = 1, k−3 = 1, q = 1. Тогда a = −13, c = 3 и при н. у. A01 = 0.3 получим b1 = 4.3, A∞1 ≈ 0.36, D1 = −117.41/2, а при A02 = 0 получим b2 = 4, A∞2 ≈ 0.33, D2 = −1211/2. Инвариант (14) по реагенту А для реакции (IV) примет вид
(4.4)
$\begin{gathered} {{K}_{A}}(t) \equiv \left[ {{{D}_{2}}{\text{arctg}}\left( {{{(6{{A}_{1}} - 13)} \mathord{\left/ {\vphantom {{(6{{A}_{1}} - 13)} {{{D}_{1}}}}} \right. \kern-0em} {{{D}_{1}}}}} \right)} \right. - \\ {{\left. { - \,\,{{D}_{1}}{\text{arctg}}\left( {{{(6{{A}_{2}} - 13)} \mathord{\left/ {\vphantom {{(6{{A}_{2}} - 13)} {{{D}_{2}}}}} \right. \kern-0em} {{{D}_{2}}}}} \right)} \right]} \mathord{\left/ {\vphantom {{\left. { - \,\,{{D}_{1}}{\text{arctg}}\left( {{{(6{{A}_{2}} - 13)} \mathord{\left/ {\vphantom {{(6{{A}_{2}} - 13)} {{{D}_{2}}}}} \right. \kern-0em} {{{D}_{2}}}}} \right)} \right]} {{{K}_{{A0}}}}}} \right. \kern-0em} {{{K}_{{A0}}}}} = 1, \\ \end{gathered} $
где KA0 ≡ D2arctg(−11.2/D1) − D1arctg(−13/D2) (рис. 3).

Рис. 3.

Концентрационные зависимости A1(t), A2(t) и А-инвариант (4.4) для реакции (IV) при k1= 4, k−1 = 1, k2 = 1, k−2 = 0.5, k3 = 1, k−3 = 1, q = 1 и н. у. A01 = 0.3, A02 = 0: 1 – A1(t), 2 – A2(t), 3 – KA(t).

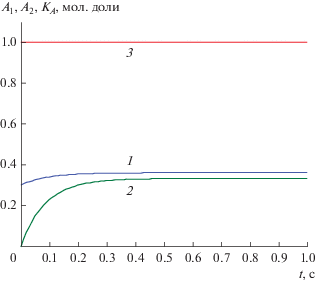
Как видно на рис. 3 KA(t) не зависит от времени и является точным инвариантом. Инварианты по реагентам B и С находятся из (4.4) заменами A1 = B1, A1 = 1 − С1 и A2 = B2, A2 = 1 − С2 соответственно.

Пример 4. Одностадийная реакция с тремя реагентами

(V)
${\mathbf{A}} + {\mathbf{B}} = {\mathbf{C}}$
в открытой системе описывается уравнениями вида (5.1)–(5.3):
(5.1)
$A{\kern 1pt} ' = - {{k}_{1}}AB + {{k}_{{ - 1}}}C + q({{A}_{0}} - A),$
(5.2)
$B{\kern 1pt} ' = - {{k}_{1}}AB + {{k}_{{ - 1}}}C + q({{B}_{0}} - B),$
(5.3)
$C{\kern 1pt} ' = {{k}_{1}}AB - {{k}_{{ - 1}}}C + q({{A}_{0}} - A).$
В этой реакции участвуют три реагента (n = 3) и два комплекса (A + B) и С. Из (6) находим Rs = 1, Rk = 1, N = 2, Ns = 2 и Nk = 0, т.е. выполняется условие (7), и есть два ЛЗС A + С = 1 и B + C = 1, которые позволяют понизить порядок системы (5.1)–(5.3) на два и заменить ее одним ОДУ
(5.4)
$A{\kern 1pt} ' = - {{k}_{1}}{{A}^{2}} + {{k}_{{ - 1}}}(1 - A) + q({{A}_{0}} - A),$
где c = −k1, a = −(k−1 + q) < 0, b = k−1+ qA0 > 0. Условия физичности (11) реализуются, например, при k1= 4, k−1 = 1, q = 1. Тогда a = −2, c = −4 и при н. у. A01 = 1 получим b1 = 2, D1 = −361/2, а при A02 = 0 получим b2 = 1, D2 = −201/2. Инвариант (14) по реагенту А для реакции (V) примет вид
(5.5)
$\begin{gathered} {{K}_{A}}(t) \equiv \left[ {{{D}_{2}}{\text{arctg}}\left( {{{( - 2 - 8{{A}_{1}})} \mathord{\left/ {\vphantom {{( - 2 - 8{{A}_{1}})} {{{D}_{1}}}}} \right. \kern-0em} {{{D}_{1}}}}} \right)} \right. - \\ {{\left. { - \,\,{{D}_{1}}{\text{arctg}}\left( {{{( - 2 - 8{{A}_{1}})} \mathord{\left/ {\vphantom {{( - 2 - 8{{A}_{1}})} {{{D}_{2}}}}} \right. \kern-0em} {{{D}_{2}}}}} \right)} \right]} \mathord{\left/ {\vphantom {{\left. { - \,\,{{D}_{1}}{\text{arctg}}\left( {{{( - 2 - 8{{A}_{1}})} \mathord{\left/ {\vphantom {{( - 2 - 8{{A}_{1}})} {{{D}_{2}}}}} \right. \kern-0em} {{{D}_{2}}}}} \right)} \right]} {{{K}_{{A0}}}}}} \right. \kern-0em} {{{K}_{{A0}}}}} = 1, \\ \end{gathered} $
где KA0 ≡ D2arctg(−10/D1) − D1arctg(−2/D2).

Пример 5. Трехстадийная реакция с тремя реагентами

(VI)
$1)\,\,{\mathbf{A}} = {\mathbf{B}},\,\,\,\,2)\,\,2{\mathbf{B}} = 2{\mathbf{С}},\,\,\,\,3)\,\,{\mathbf{A}} + {\mathbf{B}} = 2{\mathbf{С}}.$
Динамика этой реакции в открытой системе описывается уравнениями:
(6.1)
$A{\kern 1pt} ' = - {{k}_{1}}A + {{k}_{{ - 1}}}B - {{k}_{3}}AB + {{k}_{{ - 3}}}{{C}^{2}} + q({{A}_{0}} - A),$
(6.2)
$\begin{gathered} B{\kern 1pt} ' = {{k}_{1}}A - {{k}_{{ - 1}}}B - 2{{k}_{2}}{{B}^{2}} + {\text{ }}2{{k}_{{ - 2}}}{{С}^{2}} - \\ - \,\,{{k}_{3}}AB + {{k}_{{ - 3}}}{{С}^{2}} + q({{B}_{0}} - B), \\ \end{gathered} $
(6.3)
$\begin{gathered} С{\kern 1pt} ' = 2{{k}_{2}}{{B}^{2}} - 2{{k}_{{ - 2}}}{{С}^{2}} + {\text{ }}2{{k}_{3}}AB - \\ - \,\,2{{k}_{{ - 3}}}{{С}^{2}} + q({{С}_{0}} - С). \\ \end{gathered} $
В этой реакции участвуют три реагента (n = 3) и пять комплексов А, В, 2B, 2C и (A + B). Из (6) находим Rs = 2, Rk = 2, N = 1, Ns = 1 и Nk = 0, т.е. существует только один ЛЗС A + B + C = 1, и условия (7) не выполняются. Значит, схема может описывать химическую реакцию, но инвариантов вида (14) нет.

Пример 6. Двухстадийная бимолекулярная реакция

(VII)
$1)\,\,{\mathbf{2A}} \to {\mathbf{B}},\,\,\,\,2)\,\,2{\mathbf{A}} \to {\mathbf{С}} + {\mathbf{D}}$
в открытой системе описывается уравнениями:
(7.1)
$\begin{gathered} A{\kern 1pt} ' = - 2\left( {{{k}_{1}} + {{k}_{2}}} \right){{A}^{2}} + q({{A}_{0}} - A), \\ B' = {{k}_{1}}{{A}^{2}} + q({{B}_{0}} - B), \\ \end{gathered} $
(7.2)
$С{\kern 1pt} ' = {{k}_{2}}{{A}^{2}} + q({{С}_{0}} - С),\,\,\,\,D{\kern 1pt} ' = {{k}_{2}}{{A}^{2}} + q({{D}_{0}} - D).$
В этой реакции участвуют четыре реагента (n = 4) и только один комплекс А. Из (6) находим Rs = 2, Rk = 1, N = 3, Ns = 2 и Nk = 1, т.е. условия (7) выполняются, и есть три независимых ЛЗС A + 2B + + 2C = 1, A + 2B + 2D = 1 и k1A + 2(k1 + k2)B = 1. Значит, эта система эквивалентна одному любому из уравнений (7.1), (7.2). Например, первое из них имеет вид (9) при с = −2(k1 + k2)1, a = −q, b = qA0. Для этих значений условия физичности (11) выполняются всегда. Пусть при k1= 1, k2 = 1, q = 1, тогда для первого н. у. A01 = 1 получим c = −4, a = −1, b1 = 1, D1 = −171/2, а для второго н. у. A02 = 1/2 получим b2 = 1/2, D2 = −91/2. Подставим эти значения в (14) и найдем A-инвариант
(7.3)
$\begin{gathered} {{K}_{A}}\left( t \right) \equiv \left[ {{{D}_{2}}{\text{arctg}}\left( {{{( - 1 - 8{{A}_{1}})} \mathord{\left/ {\vphantom {{( - 1 - 8{{A}_{1}})} {{{D}_{1}}}}} \right. \kern-0em} {{{D}_{1}}}}} \right) - } \right. \\ {{\left. { - \,\,{{D}_{1}}{\text{arctg}}\left( {{{( - 1 - 8{{A}_{2}})} \mathord{\left/ {\vphantom {{( - 1 - 8{{A}_{2}})} {{{D}_{2}}}}} \right. \kern-0em} {{{D}_{2}}}}} \right)} \right]} \mathord{\left/ {\vphantom {{\left. { - \,\,{{D}_{1}}{\text{arctg}}\left( {{{( - 1 - 8{{A}_{2}})} \mathord{\left/ {\vphantom {{( - 1 - 8{{A}_{2}})} {{{D}_{2}}}}} \right. \kern-0em} {{{D}_{2}}}}} \right)} \right]} {{{K}_{{A0}}}}}} \right. \kern-0em} {{{K}_{{A0}}}}} = 1, \\ \end{gathered} $
где KA0 ≡ D2arctg(−9/D1) − D1arctg(−5/D2).

Пример 7. Тримолекулярная реакция с двумя реагентами

(VIII)
$1)\,\,{\mathbf{A}} = {\mathbf{B}},\,\,\,\,2)\,\,2{\mathbf{A}} = {\mathbf{2B}},\,\,\,\,3)\,\,3{\mathbf{A}} = 3{\mathbf{B}}$
в открытой системе описывается уравнениями:
(8.1)
$\begin{gathered} A{\kern 1pt} ' = - {{k}_{1}}A + {{k}_{{ - 1}}}B - 2{{k}_{2}}{{A}^{2}} + {\text{ }}2{{k}_{{ - 2}}}{{B}^{2}} - \\ - \,\,3{{k}_{3}}{{A}^{3}} + {\text{ }}3{{k}_{{ - 3}}}{{B}^{3}} + q({{A}_{0}} - A), \\ \end{gathered} $
(8.2)
$\begin{gathered} B{\kern 1pt} ' = {{k}_{1}}A - {{k}_{{ - 1}}}B + {\text{ }}2{{k}_{2}}{{A}^{2}} - 2{{k}_{{ - 2}}}{{B}^{2}} + \\ + \,\,3{{k}_{3}}{{A}^{3}} - 3{{k}_{{ - 3}}}{{B}^{3}} + q({{B}_{0}} - B). \\ \end{gathered} $
Из (6) находим Rs = 1, Rk = 1, N = 1, Ns = 1 и Nk = 0, т.е условия (7) выполняются, и в данной реакции есть только один ЛЗС вида A + B = 1 и один независимый реагент, а система (8.1)–(8.2) эквивалентна уравнению
(8.3)
$\begin{gathered} A{\kern 1pt} ' = - {{k}_{1}}A + {{k}_{{ - 1}}}(1 - A) - 2{{k}_{2}}{{A}^{2}} + {\text{ }}2{{k}_{{ - 2}}}{{(1 - A)}^{2}} - \\ - \,\,3{{k}_{3}}{{A}^{3}} + {\text{ }}3{{k}_{{ - 3}}}{{(1 - A)}^{3}} + q({{A}_{0}} - A), \\ \end{gathered} $
где d = −3(k3 + k−3), c = 2k−2 + 9k−3 − 2k2, a = −(k−1 + + 4k−2 + 9k−3 + k1 + q), b = 2k−2 + k−1 + 3k−3 + qA0.

Для этого уравнения, согласно (19), инвариант по реагенту А запишется как

(8.4)
${{K}_{A}}\left( t \right) \equiv {{({{L}_{1}} - {{L}_{2}})} \mathord{\left/ {\vphantom {{({{L}_{1}} - {{L}_{2}})} {({{L}_{{01}}} - {{L}_{{02}}})}}} \right. \kern-0em} {({{L}_{{01}}} - {{L}_{{02}}})}} = 1,$
где L1 ≡ ln(A1 − A1∞1)/s11 + ln(A1 − A2∞1)/s21 + ln(A1 − − A3∞1)/s31, L2 ≡ ln(A2 − A1∞2)/s12 + ln(A2 − A2∞2)/s22 + + ln(A2 − A3∞2)/s32, L01 ≡ ln(A01 − A1∞1)/s11 + ln(A01 − A2∞1)/s21 + ln(A01 − A3∞1)/s31, L02 ≡ ln(A02 − A1∞2)/ s12 + ln(A02 − A2∞2)/s22 + ln(A02 − A3∞2)/s32. Здесь s11 = 3dA1∞12 + 2cA1∞1 + a, s21 = 3dA2∞12 + 2cA2∞1 + a, s31 = 3dA3∞12 + 2cA3∞1 + a, s12 = 3dA1∞22 + 2cA1∞2 + a, s22 = 3dA2∞22 + 2cA2∞2 + a, s32 = 3dA3∞22 + 2cA3∞2 + a. Пусть k1= 1, k−1 = 1, k2 = 1, k−2 = 1, k3 = 1, k−3 = 1, q = 1, тогда d = −6, c = 9, a = −16, b = 6 + A0. Условие физичности (17) принимает вид b(–13 + b) < 0 и выполняется для граничных н. у. A01 = 1, A02 = 0, B01 = 0, B02 = 1. Тогда получим b1 = 7, A1∞1, 2∞1, 3∞1 ≈ ≈ {0.54, 0.48 ± 1.38i} и b2 = 6, A1∞2, 2∞2, 3∞2 ≈ {0.46, 0.52 ± 1.38i}. Для других н. у., например, A01 = = 3/4, A02 = 1/4, B01 = 1/4, B02 = 3/4 получим b1 = = 6.75, A1∞1, 2∞1, 3∞1 ≈ {0.52, 0.49 ± 1.38i} и b2 = 6.25, A1∞2, 2∞2, 3∞2 ≈ {0.48, 0.51 ± 1.38i}. Инвариант (8.4) показан на рис. 4.

Рис. 4.

Концентрационные зависимости A1(t), A2(t) и А-инвариант (8.4) для реакции (VIII) при k1= 1, k−1 = 1, k2 = 1, k−2 = 1, k3 = 1, k−3 = 1, q = 1 и н. у. A01 = 3/4, A02 = 1/4: 1 – A1(t), 2 – A2(t), 3 – KA(t).

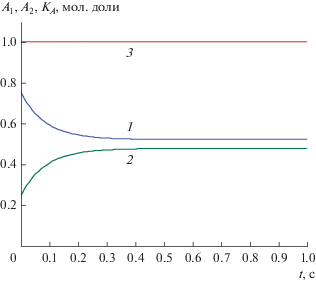
Как видно на рис. 4, А-инвариант не зависит от времени и является точным. Инварианты по реагенту B находятся из (8.4) заменами A1 = 1 − B1 и A2 = 1 − B2.

ЗАКЛЮЧЕНИЕ

В работе получены аналитические выражения для определения точных автономных инвариантов многостадийных нелинейных химических реакций, протекающих в открытых изотермических системах с участием двух и более реагентов в рамках закона действующих масс. Найдены соотношения, связывающие неравновесные концентрации реагентов, измеренные в двух экспериментах с разными начальными условиями (не обязательно граничными), которые остаются строго постоянными в течение всей реакции (ММЭ-инварианты). Приведены условия применимости этих соотношений и примеры конкретных химических реакций с участием нескольких реагентов. Найденные для этих реакций инвариантные кривые сопоставлены с кривыми изменения концентраций в течение всего переходного процесса. Показано, что на графиках зависимости концентраций реагентов от времени точные инварианты таких реакций наблюдаются в виде строго горизонтальных линий. Полученные результаты расширяют представления о динамических характеристиках нелинейных химических реакций и могут быть использованы при решении обратных задач и моделировании химических процессов в реакторах идеального смешения. Подчеркнем, что ММЭ-инварианты представляют собой альтернативную, существенно отличающуюся от МДЭ-инвариантов [7–18] форму автономных временных инвариантов химических реакций. ММЭ-инварианты – это инварианты совсем другого рода, и они рассчитываются на основе механизма и кинетических параметров реакции в виде сложных функций от концентраций одного из реагентов, измеренных в нескольких экспериментах с любыми начальными условиями в закрытых и открытых системах.

Список литературы

  1. Корзухин М.Д. // Журн. физ. хим. 1972. Т. 46. № 7. С. 1845.

  2. Вольперт А.И., Худяев С.И. Анализ в классах разрывных функций и уравнения математической физики. М.: Наука, 1975. 394 с.

  3. Prelle M.J., Singer M.F. // Proc. ACM Symp. of Symbolic and Algebraic Computation. Snowbird Utah, 1981. P. 30.

  4. Яблонский Г.С., Быков В.И., Горбань А.Н. Кинетические модели каталитических реакций. Новосибирск: Наука, 1983. 254 с.

  5. Алексеев Б.В., Кольцов Н.И., Федотов В.Х. // Журн. физ. химии. 1988. Т. 62. № 11. С. 3069.

  6. Алексеев Б.В., Кольцов Н.И., Федотов В.Х. // Журн. физ. химии. 1992. Т. 66. № 12. С. 3219.

  7. Yablonsky G.S., Constales D., Marin G.B. // Chem. Eng. Sci. 2010. V. 65. P. 6065.

  8. Yablonsky G.S., Gorban A.N., Constales D., Galvita V.V., Marin G.B. // Europhys. Lett. 2011. V. 93. № 2. P. 20 004.

  9. Constales D., Yablonsky G.S., Galvita V.V., Marin G.B. // Chem. Eng. Sci. 2011. V. 66. P. 4683.

  10. Yablonsky G.S., Constales D., Marin G.B. // Chem. Eng. Sci. 2011. V. 66. P. 111.

  11. Constales D., Yablonsky G.S., Marin G.B. // Chem. Eng. Sci. 2012. V. 73. P. 20.

  12. Constales D., Yablonsky G.S., Marin G.B. // Computers and Mathematics with Applications. 2013. V. 65. № 10. P. 1614.

  13. Yablonsky G.S. // Theor. Found. Chem. Eng. 2014. V. 48. № 5. P. 608.

  14. Branco-Pinto D., Yablonsky G., Marin G., Constales D. // Entropy. 2015. V. 17. № 10. P. 6783.

  15. Branco P.D., Yablonsky G.S., Marin G.B., Constales D. // Chem. Eng. Sci. 2017. V. 158. P. 370.

  16. Peng B., Yablonsky G.S., Constales D., Marin G.B. // Chem. Eng. Sci. 2018. V. 191. P. 262.

  17. Branco P.D., Yablonsky G.S., Marin G.B., Constales D. // Chem. Eng. Sci. 2018. V. 184. P. 25.

  18. Yablonsky G.S., Branco P.D., Marin G.B., Constales D. // Chem. Eng. Sci. 2019. V. 196. P. 384.

  19. Федотов В.Х., Кольцов Н.И. // Изв. вузов. Химия и хим. технология. 2016. Т. 59. № 5. С. 72.

  20. Федотов В.Х., Кольцов Н.И. // Вестн. технол. ун-та. 2018. Т. 21. № 9. С. 113.

  21. Федотов В.Х., Кольцов Н.И. // Вестн. технол. ун-та. 2018. Т. 21. № 11. С. 195.

  22. Федотов В.Х., Кольцов Н.И., Косьянов П.М. // Вестн. технол. ун-та. 2018. Т. 21. № 12. С. 181.

  23. Федотов В.Х., Кольцов Н.И. // Вестн. технол. ун-та. 2019. Т. 22. № 1. С. 119.

  24. Федотов В.Х., Кольцов Н.И. // Хим. физика. 2019. Т. 38. № 4. С. 23.

  25. Федотов В.Х., Кольцов Н.И. // Изв. вузов. Химия и хим. технология. 2019. Т. 62. № 6. С. 47.

  26. Федотов В.Х., Кольцов Н.И. // Изв. вузов. Химия и хим. технология. 2019. Т. 62. № 8. С. 76.

  27. Федотов В.Х., Кольцов Н.И. // Кинетика и катализ. 2019. Т. 60. № 6. С. 756.

  28. Корн Г., Корн Т. Справочник по математике. М.: Наука, 1978.

  29. Abell M.L., Braselton J.P. Differential Equations with Mathematica. London–N.Y.: Acad. Press, 2016.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Кинетика и катализ

Архивы выпусков Информация о журнале Отправить рукопись в журнал