1. На главную
  2. Электронные версии
  3. Кинетика и катализ
  4. T. 63, № 6, 2022

Кинетика и катализ, 2022, T. 63, № 6, стр. 724-726

О множественности стационарных состояний в простой двухстадийной каталитической реакции

Н. И. Кольцов *

ФГБОУ ВО Чувашский государственный университет им. И.Н. Ульянова, химико-фармацевтический факультет
428015 Чебоксары, Московский просп., 15, Россия

* E-mail: koltsovni@mail.ru

Поступила в редакцию 21.02.2022
После доработки 07.05.2022
Принята к публикации 13.07.2022

Полный текст (PDF)

Аннотация

Установлена возможность существования мультимножественности стационарных состояний кинетической природы в простейшей двухстадийной каталитической реакции М. Темкина, протекающей по неидеальному кинетическому закону Марселина–Де Донде в открытой безградиентной изотермической системе.

Ключевые слова: двухстадийная каталитическая реакция, неидеальная кинетика, мульти-множественность стационарных состояний

ВВЕДЕНИЕ

Известно, что простейшая двухстадийная каталитическая реакция в открытой безградиентной изотермической системе в рамках идеального кинетического закона (КЗ) действующих масс (ЗДМ) обладает единственным стационарным состоянием (с. с.) [1]. В настоящем сообщении показано, что если эта реакция протекает по неидеальному КЗ Марселина–Де Донде [2], то для нее возможно существование множественности с. с. не только в виде двух устойчивых с. с. (бистационарная множественность), но трех и более (мультистационарная множественность) устойчивых с. с.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Пусть каталитическая реакция A = B протекает по схеме М.И. Темкина [1]:

${\text{i}}){\text{ A}} + {\text{Z}} = {\text{X}},\,\,\,\,{\text{ii}})\,{\text{X}} = {\text{Z}} + {\text{B}},~$ (I)
где А и В – основные вещества; X – промежуточное вещество; Z – свободный центр на поверхности катализатора. Динамика этой реакции в открытой безградиентной изотермической системе при избытке основных веществ (квазистационарный по основным веществам режим) описывается дифференциальным уравнением
(1)
$x_{t}^{'} = {{r}_{1}}--{{r}_{2}}$
и законом сохранения количества катализатора (законом сохранения массы)
(2)
$x + z = 1,$
где x и z – концентрации промежуточного вещества X и свободных центров Z на поверхности катализатора, мол. доли; t – время, с; r1, r2 – скорости первой и второй стадий, 1/с, задаваемые некоторым неидеальным КЗ. В с. с. $x_{t}^{'}$ = 0 и из (1) следует:
(3)
$~r = r_{1}^{\infty } = r_{2}^{\infty },$
где r, $r_{1}^{\infty },$ $r_{2}^{\infty }$ – стационарные скорости реакции и стадий, 1/с. Для неидеального КЗ Марселина–Де Донде (МДД) [2] скорости стадий реакции (I) запишутся:
(4)
$\begin{gathered} {{r}_{1}} = {{w}_{ + }}_{1}\exp {{\mu }_{z}}--{{w}_{{--1}}}\exp {{\mu }_{x}}, \\ {{r}_{2}} = {{w}_{ + }}_{2}\exp {{\mu }_{x}}--{{w}_{{--2}}}\exp {{\mu }_{z}},~ \\ \end{gathered} $
(5)
${{\mu }_{x}} = {{\mu }_{x}}_{0} + {\text{ln}}{{f}_{x}},\,\,\,\,{{\mu }_{z}} = {{\mu }_{z}}_{0} + {\text{ln}}{{f}_{z}},$
где w+1 = k+1A, w–1 = k–1, w+2 = k+2, w–2 = k–2B – частоты стадий; k+1, k–1, k+2, k–2 – константы скоростей стадий, 1/с; A, B – концентрации основных веществ, мол. доли; μx, μz – псевдохимические (с точностью до множителя) потенциалы основных веществ, б/р; fx, fz – функции от концентраций промежуточного вещества и свободных центров, б/р.

При идеальной кинетике ЗДМ функции fx и fz в (5) предполагаются линейными по концентрациям промежуточного вещества и свободных центров:

(6)
${{f}_{х}} = x,\,\,\,\,{{f}_{z}} = z = 1{\text{ }}--х.$

В неидеальной кинетике МДД функции fx и fz допускают нелинейные зависимости от концентраций промежуточных веществ, точный вид которых не известен (см., например, [4, 5]). Разложим эти функции в ряд, считая, что они зависят от концентрации только одного промежуточного вещества, и ограничимся при этом членами пятого порядка точности по х и линейными по z, т.е.:

(7)
${{f}_{x}} = a{{x}^{5}} + b{{x}^{4}} + c{{x}^{3}} + d{{x}^{2}} + ex{\text{ }} + x,\,\,\,\,{{f}_{z}} = z,$
где коэффициенты разложения пропорциональны первой, второй, третьей, четвертой и пятой производным функции fx, т.е. стационарной скорости реакции, ускорению и т.д. вблизи стационарного состояния. Областью определения такой модели (7) является малая окрестность любого стационарного состояния, учитывающая возможную неидеальность стационарной адсорбции промежуточного вещества. Для идеальной кинетики а = b = с = d = e = 0 и из (7) следует (6).

Тогда кинетическая модель (1)–(2), (7) запишется:

(8)
$\begin{gathered} x_{t}^{'} = ({{w}_{ + }}_{1} + {{w}_{{--2}}})-- \\ - \,\,({{w}_{{--1}}} + {{w}_{{ + 2}}})(a{{x}^{5}} + b{{x}^{4}} + c{{x}^{3}} + d{{x}^{2}})-- \\ - \,\,[e({{w}_{{--1}}} + {{w}_{{ + 2}}}){\text{ }} + {\text{ }}({{w}_{ + }}_{1} + {{w}_{{--2}}})]x, \\ \end{gathered} $
из которой в с. с. $x_{t}^{'}$ = 0 следует алгебраическое полиномиальное уравнение
(9)
$a{{x}^{5}} + b{{x}^{4}} + c{{x}^{3}} + d{{x}^{2}} + \left( {e{\text{ }} + p + 1} \right)x--p = 0,$
где p ≡ (w+1 + w–2)/(w–1 + w+2). Стационарная скорость реакции (3) с учетом (7) равна

(10)
$\begin{gathered} r = {{w}_{ + }}_{1}\left( {1{\text{ }}--x} \right)--{{w}_{{--1}}}(a{{x}^{5}} + b{{x}^{4}} + \\ {\text{ + }}\,\,c{{x}^{3}} + d{{x}^{2}} + ex{\text{ }} + x).~~ \\ \end{gathered} $

Неидеальный КЗ должен удовлетворять термодинамическим ограничениям [3]. Первое из этих ограничений означает, что матрица поправок для химических потенциалов (6) должна быть симметричной, что очевидно выполняется, т. к. она имеет диагональную структуру. Второе ограничение означает, что матрица Якоби для частных производных химических потенциалов

(11)
$\begin{gathered} \partial {{\mu }_{x}}{\text{/}}\partial x = [(5a{{x}^{4}} + 4b{{x}^{3}} + 3c{{x}^{2}} + \\ + \,\,2dx + e + 1){\text{/(}}a{{x}^{5}} + b{{x}^{4}} + c{{x}^{3}} + d{{x}^{2}} + ex + 1{\text{)}}], \\ \partial {{\mu }_{z}}{\text{/}}\partial x = {\text{ }}0,\,\,\,\,\partial {{\mu }_{z}}{\text{/}}\partial z = 1{\text{/}}z > 0 \\ \end{gathered} $
должна быть положительно определенной, что с учетом (9) выполняется при условии:

(12)
$g\left( x \right) \equiv 5a{{x}^{4}} + 4b{{x}^{3}} + 3c{{x}^{2}} + 2dx + e + 1{\text{ }} > {\text{ }}0.$

Покажем, что это условие совместимо с мультимножественностью с. с., при которой существуют пять с. с., три из которых – устойчивы и физичны, а два – неустойчивы.

Зададим пять заведомо физичных значений координат с. с., например x∞= (0.05, 0.1, 0.2, 0.4, 0.5), которые реализуются при

(13)
$\begin{gathered} a = 1,\,\,\,\,b = --1.2500,\,\,\,\,c = 0.5500, \\ d = --0.1025,\,\,\,\,e = --0.9923,\,\,\,\,p = 0.0002. \\ \end{gathered} $

Эти значения сохраняются для бесконечного множества наборов констант, например,

(14)
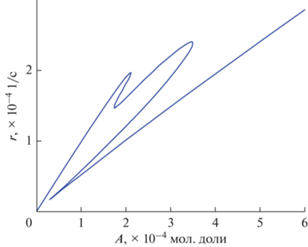
${{k}_{ + }}_{2} = 1,\,\,\,\,{{k}_{{--1}}} = 0,\,\,\,\,{{k}_{{--2}}} = 0,\,\,\,\,{{k}_{ + }}_{1}A = p{{k}_{ + }}_{2} = p.$

Нетрудно убедиться, что первое, третье и пятое с. с. устойчивы. Условие (12) выполняется в каждом из этих с. с. g(0.05) = 9.8125 × 10–4, g(0.2) = 7.00 × ×  10–4, g(0.5) = 0.0052. На рис. 1 приведена зависимость стационарной скорости r(А), показывающая существование пяти с. с., три из которых устойчивы и физически реализуемы для реакции (I) при определенных значениях концентрации основного вещества А.

Рис. 1.

Зависимость стационарной скорости реакции (I) от концентрации вещества А при k+1 = 1 1/с, k–1 = 0 1/с, k+2 = 1 1/с, k–2 = 0 1/с.

ЗАКЛЮЧЕНИЕ

Таким образом, даже в простой линейной по промежуточным веществам двухстадийной каталитической реакции, протекающей по неидеальному кинетическому закону Марселина–Де Донде в квазистационарном по основным веществам режиме в открытой безградиентной изотермической системе, может возникать мультимножественность стационарных состояний.

Список литературы

  1. Темкин М.И. // Кинетика и катализ. 1976. Т. 17. № 5. С. 1095.

  2. Де Донде Т., Ван Риссельберг П. Термодинамическая теория сродства. Москва: Металлургия, 1984. (De Donde, Th., Van Rysselberghe, P. Thermodynamic Theory of Affinity. Stanford University Press, Stanford University, Stanford, 1936.)

  3. Яблонский Г.С., Быков В.И., Горбань А.Н. Кинетические модели каталитических реакций. Новосибирск: Наука, 1983.

  4. Зыскин А.Г., Снаговский Ю.С, Слинько М.Г. // Кинетика и катализ. 1981. Т. 22. № 4. С. 1031.

  5. Горбань А.Н. Обход равновесия (уравнения химической кинетики и их термодинамический анализ). Новосибирск: Наука, 1984.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Кинетика и катализ

Архивы выпусков Информация о журнале Отправить рукопись в журнал