Коллоидный журнал, 2019, T. 81, № 1, стр. 10-15
Локальное нормальное давление в щели между нанодиском и поверхностью твердого тела с учетом дисперсионных сил
Е. Н. Бродская 1, *, А. И. Русанов 1
1 Санкт-Петербургский государственный университет
199034 Санкт-Петербург, Университетская наб., 7, Россия
* E-mail: e.brodskaya@spbu.ru
Поступила в редакцию 01.07.2018
Аннотация
На основе тензора напряжений Ирвинга–Кирквуда и парного потенциала дисперсионных сил без запаздывания проведен расчет локального нормального давления на торцевой поверхности нанодиска, обращенной к бесконечной плоской поверхности твердого тела и находящейся от нее на некотором расстоянии. Аналитическими и численными методами исследована зависимость нормального давления как от радиуса и толщины нанодиска, так и от расстояния нанодиска до твердой поверхности. Путем сопоставления общей силы взаимодействия нанодиска с твердым телом, рассчитанной, с одной стороны, методом Гамакера, а с другой – путем интегрирования локального давления на торце нанодиска, проведена оценка небольшого вклада боковой поверхности нанодиска в общую силу взаимодействия.
Характерным признаком наноразмерных систем является зависимость их свойств от размеров составляющих их частиц. Это относится не только к общим свойствам систем, но и к локальным характеристикам, таким, например, как распределение силового поля и вещества вблизи наночастиц. В коллоидной науке часто рассматриваются задачи, связанные с зависимостью взаимодействия частиц раствора от расстояния до твердой поверхности. При этом используют формулы для сил взаимодействия либо для двух макроскопических тел, либо сферической частицы с плоской поверхностью, впервые полученные Гамакером [1] и не учитывающие локальных эффектов. Учету локальных эффектов в наноразмерных системах был посвящен ряд наших предыдущих работ. В [2–9] мы рассматривали поведение локального тензора давления в конечных круглых щелях между континуальными твердыми телами с дисперсионными силами. Были рассмотрены случаи щели между бесконечной плоскостью твердого тела и торцом полубесконечного цилиндра [2, 3], между торцами двух полубесконечных цилиндров [4–7], между двумя цилиндрическими дисками [8]. Влияние конечных продольных размеров щели (краевой эффект) было оценено для среднего расклинивающего давления щели. Важным следствием полученных локальных зависимостей компонент тензора давления было определение линейного натяжения края щели [9]. Очевидно, что все эти явления становятся особенно существенными при обращении к наноразмерным системам, что было подтверждено молекулярно-динамическим моделированием [10, 11].
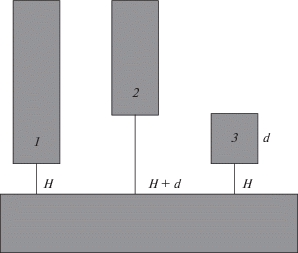
Данное сообщение посвящено рассмотрению локального нормального давления на поверхности нанодиска, находящегося вблизи твердого тела и ориентированного параллельно плоской поверхности твердого тела. По сравнению с нашей работой [2] задача усложняется тем, что вместо полубесконечного цилиндра (бесконечно толстого диска) фигурирует диск конечной толщины. Тем самым добавляется еще одна переменная – толщина диска. Как и раньше, будем исходить из тензора давления Ирвинга–Кирквуда [12]. Особенностью его определения как локального тензора давления через элементарную площадку является такой выбор способа пространственного интегрирования межмолекулярных парных сил, при котором вектор силы пересекает эту площадку. Поэтому при рассмотрении локальной силы, действующей на торец диска, будут учитываться только те пары взаимодействующих частиц, для которых соединяющая их прямая линия пересекает торец. Подробное описание процедуры расчета нормальной компоненты тензора давления в нанощели дано в [2]. Однако в случае конечного диска такая процедура и не потребуется. Для наших оценок достаточно более простого подхода, который состоит в следующем. Как схематично показано на рис. 1, рассматриваемая система может быть сконструирована как разность двух других систем, расчеты для которых можно провести по алгоритму, изложенному в [2]. Поэтому тензор давления на внутренней поверхности диска толщиной d на расстоянии H над поверхностью твердого тела будет результатом разности тензоров для двух щелей шириной H и H + d с полубесконечными цилиндрами [2].
Воспользуемся этой схемой и найдем нормальное давление на внутренней поверхности диска. Как и в [2], ограничимся пустой щелью и дисперсионными взаимодействиями между телами, потенциал которых на больших расстояниях R между молекулами i и j дается асимптотическим выражением
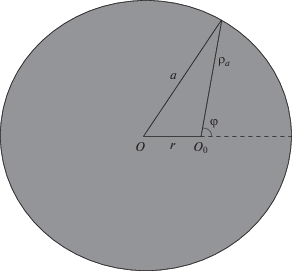
где ${{A}_{{ij}}}$ – константа. В качестве исходного выражения возьмем формулу (21) из [2] для нормальной компоненты локального тензора давления Ирвинга–Кирквуда [12] на поверхности торца цилиндра в щели между бесконечной плоскостью твердого тела и полубесконечным цилиндром радиуса a(2)
${{p}_{\operatorname{N} }}(H,r,a) = - \frac{{\pi {{A}_{{12}}}{{c}_{1}}{{c}_{2}}}}{{6{{H}^{3}}}}\left[ {1 - \frac{3}{{16\pi }}\int\limits_0^{2\pi } {d\varphi } F\left( b \right)} \right],$(3)
$F(b) \equiv {{\left[ \begin{gathered} 16 - 768{{b}^{2}} + 288{{b}^{4}} + 1024{{b}^{6}} - 48{{b}^{8}} + \pi (3{{b}^{9}} + 108{{b}^{7}} - \hfill \\ - \,\,990{{b}^{5}} + 780{{b}^{3}} - 45b) - (960{{b}^{6}} - 2304{{b}^{4}} + 576{{b}^{2}})\ln b \hfill \\ \end{gathered} \right]} \mathord{\left/ {\vphantom {{\left[ \begin{gathered} 16 - 768{{b}^{2}} + 288{{b}^{4}} + 1024{{b}^{6}} - 48{{b}^{8}} + \pi (3{{b}^{9}} + 108{{b}^{7}} - \hfill \\ - \,\,990{{b}^{5}} + 780{{b}^{3}} - 45b) - (960{{b}^{6}} - 2304{{b}^{4}} + 576{{b}^{2}})\ln b \hfill \\ \end{gathered} \right]} 6}} \right. \kern-0em} 6}{{\left( {1 + {{b}^{2}}} \right)}^{6}},$(4)
${{\rho }_{a}}(\varphi ) = - r\cos \varphi + \sqrt {{{a}^{2}} - {{r}^{2}}{{{\sin }}^{2}}\varphi } .$В отличие от бесконечной щели локальное нормальное давление в круглой щели зависит не только от ее ширины H, но и от расстояния r до оси симметрии и от радиуса a диска. Второе слагаемое в правой части (2) описывает относительный вклад краевых эффектов Δ1, и рассчитывать его удобнее численным интегрированием (рис. 3а). Этот вклад незначителен в околоосевой области, но возрастает при приближении к краю щели, достигая 60%. Также растет он и с увеличением ширины щели.
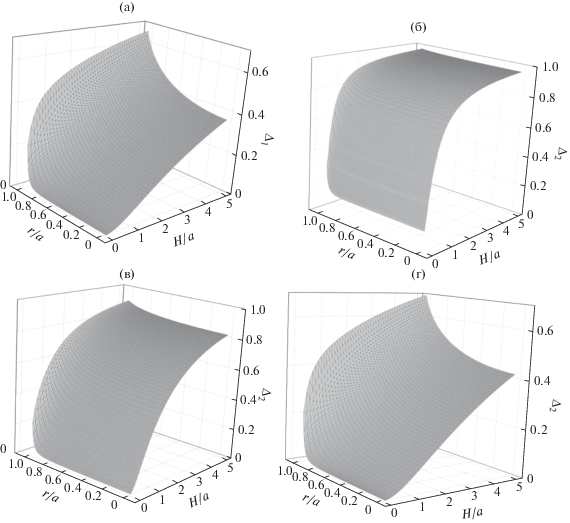
Рис. 3.
Относительные вклады в локальное нормальное давление Δ1 для бесконечного цилиндра (а) и Δ2 для диска толщиной d = 0.1a (б), d = 0.5a (в), d = 5a (г).
Чтобы получить значение нормального давления на торцевой поверхности диска толщиной d, нужно только рассчитать разницу нормального давления (2) при H и H + d. Для этой разницы правую часть (2) можно представить в виде
(5)
$\begin{gathered} {{p}_{\operatorname{N} }}(H,r,a,d) = - \frac{{\pi {{A}_{{12}}}{{c}_{1}}{{c}_{2}}}}{{6{{H}^{3}}}}\left[ {1 - ({{\Delta }_{1}} + {{\Delta }_{3}})} \right] = \\ = - \frac{{\pi {{A}_{{12}}}{{c}_{1}}{{c}_{2}}}}{{6{{H}^{3}}}}\left[ {1 - {{\Delta }_{2}}} \right], \\ \end{gathered} $(6)
${{\Delta }_{1}} = \frac{3}{{16\pi }}\int\limits_0^{2\pi } {d\varphi } F\left( {\frac{{{{\rho }_{a}}}}{H}} \right)$(7)
${{\Delta }_{3}} = \frac{{{{H}^{3}}}}{{{{{\left( {H + d} \right)}}^{3}}}} - \frac{3}{{16\pi }}\frac{{{{H}^{3}}}}{{{{{\left( {H + d} \right)}}^{3}}}}\int\limits_0^{2\pi } {d\varphi } F\left( {\frac{{{{\rho }_{a}}}}{{H + d}}} \right)$На рис. 3 сравниваются вклады в нормальное давление для бесконечного диска Δ1 и для конечных дисков различной толщины Δ2. Обе поправки незначительны по величине в узких щелях практически на всем их протяжении, но достаточно быстро растут при расширении щели. При H = 5a суммарный вклад от конечных размеров щели и толщины диска достигает 80% при d = 0.5a (рис. 3в). В случае бесконечно толстого диска (полубесконечного цилиндра) ярче проявляется локальный характер вклада, который растет при приближении к краю щели (рис. 3а). Локальные изменения в тензоре давления, безусловно, должны сопровождаться перераспределением вещества, заполняющего щель. По сравнению с бесконечно толстым диском в случае конечного диска локальный эффект несколько ослабляется при движении к краю щели, что проявляется в выравнивании локальных вкладов для фиксированной ширины щели. Для тонкого диска толщиной 0.1a локальная зависимость от расстояния до оси симметрии становится почти незаметной. Выравнивание зависимости PN от r по сравнению с бесконечным цилиндром (рис. 3а) происходит за счет вклада Δ3 от конечной толщины диска. Однако, как отмечалось выше, последний вклад ослабевает при увеличении толщины диска d и уже при d = 5a величина Δ2 почти неотличима от Δ1 (рис. 3г).
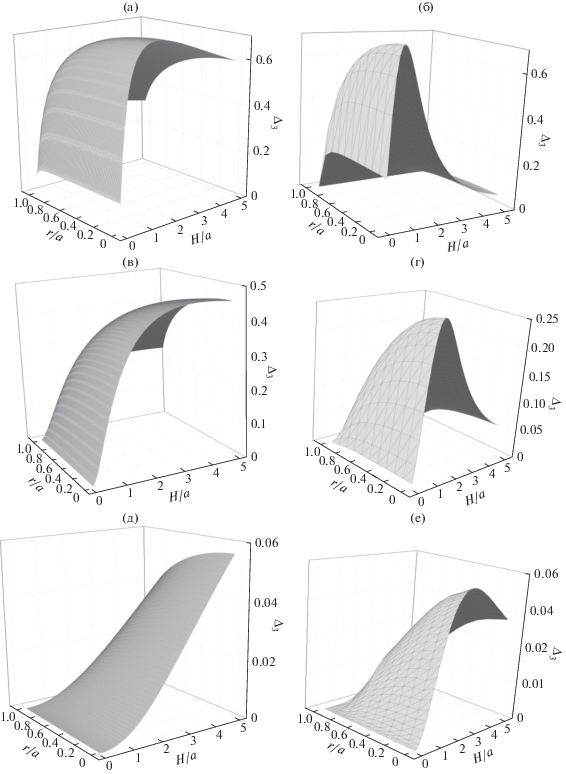
Отдельный вклад Δ3 от конечной толщины диска показан на рис. 4 для нескольких значений d, где он сравнивается с аналогичным вкладом для двух одинаковых дисков [7]. При приближении к краю диска эта локальная поправка несколько ослабевает в противоположность поведению локальной поправки Δ1 на конечную протяженность щели. Для диска толщиной 0.5a максимальные значения Δ3 составляют около 45% в середине щели и уменьшаются до 20% вблизи ее края. Более сложной оказывается ее зависимость от ширины щели. Для тонкого диска толщиной менее половины его радиуса добавка Δ3 достаточно быстро растет с увеличением ширины щели и достигает максимального значения примерно при H = 2a. Затем несколько уменьшается, оставаясь конечной величиной в отличие от случая щели между двумя одинаковыми дисками (рис. 4г–4е). С увеличением толщины диска максимум на кривой зависимости Δ3 от H исчезает. Очевидно, что при стремлении толщины диска к бесконечности величина Δ3 становится пренебрежимо малой. В целом этот вклад от учета конечной толщины диска оказывается меньше для случая двух одинаковых дисков. Наибольшие отличия в поведении этой поправки для сравниваемых систем проявляются при больших значениях ширины щели, которая стремится к нулю для случая двух дисков.
Рис. 4.
Относительные вклады в локальное нормальное давление Δ3 от конечной толщины диска для одного диска с d = 0.1a (а), d = 0.5a (в), d = 2a (д) и двух дисков с d = 0.1a (б), d = 0.5a (г), d = 2a (е).
Как указывалось выше, наш метод расчета, в отличие от классического подхода Гамакера [1], позволяет исследовать локальные величины давления, чем мы и занимались до сих пор. Но, располагая локальными данными, мы, естественно, можем рассчитать простым интегрированием и полную силу, действующую на торец диска. Конечно, эта задача решается проще по Гамакеру, но небезынтересно сравнить результаты, получаемыми двумя данными методами. Обратимся сначала к методу Гамакера. Поскольку сам родоначальник метода такую фигуру как диск не рассматривал, нам придется провести небольшой расчет. Воспользуемся известным результатом для энергии взаимодействия U(z) молекулы с твердым телом на расстоянии z от него
(9)
$U(z) = {{c}_{1}}\int\limits_{{{V}_{1}}} {d{{V}_{1}}} {{\Phi }_{{12}}} = - \frac{{\pi {{c}_{1}}{{A}_{{12}}}}}{{6{{z}^{3}}}},$(10)
${{U}_{d}} = - С \frac{{\pi a_{\operatorname{d} }^{2}d\left( {2H + d} \right)}}{{2{{H}^{2}}{{{\left( {H + d} \right)}}^{2}}}},$(12)
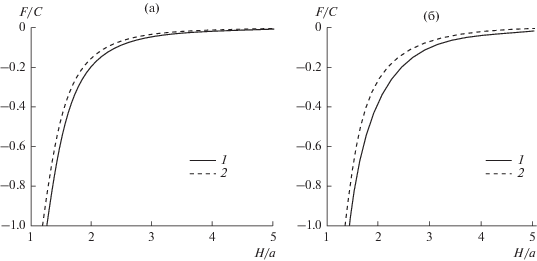
${{F}_{\operatorname{d} }} = - С \frac{{\pi a_{\operatorname{d} }^{2}d\left( {3{{H}^{2}} + 3Hd + {{d}^{2}}} \right)}}{{{{H}^{3}}{{{\left( {H + d} \right)}}^{3}}}}.$Теперь можно сравнить силу (12) и силу, получаемую суммированием полученных нами локальных нормальных давлений на торцевой поверхности диска. Такое сопоставление проведено на рис. 5 для двух значений толщины диска. Вывод: определенное небольшое различие всегда имеется. Поскольку по оси ординат откладываются отрицательные значения, нижнее положение кривой расчета по Гамакеру свидетельствует и о большей величине силы по сравнению с нашими расчетами. Легко догадаться, откуда берется эта разница. Ведь, когда нанодиск притягивается всей плоской поверхностью твердого тела, парные взаимодействия пронизывают не только торцевую, но и боковую поверхность диска. Мы же изучали тензор давления только на торце диска. Возникающая отсюда разница невелика, но растет с увеличением толщины диска. Именно она ответственна за краевые эффекты из-за неоднородного локального давления на поверхности торца диска, что проявляется в линейном натяжении на краю диска, подробно обсуждаемом в [9].
Список литературы
Hamaker H.C. // Physica. 1937. V. 4. P. 1058.
Русанов А.И., Бродская Е.Н. // Коллоид. журн. 2013. Т. 75. С. 436.
Бродская Е.Н., Русанов А.И. // Коллоид. журн. 2014. Т. 76. С. 568.
Бродская Е.Н., Русанов А.И. // Коллоид. журн. 2014. Т. 76. С. 573.
Бродская Е.Н., Русанов А.И. // Коллоид. журн. 2014. Т. 76. С. 698.
Бродская Е.Н., Русанов А.И. // Коллоид. журн. 2014. Т. 76. С. 706.
Бродская Е.Н., Русанов А.И. // Коллоид. журн. 2015. Т. 77. С.705.
Бродская Е.Н., Русанов А.И. // Коллоид. журн. 2015. Т. 77. С. 582.
Rusanov A.I., Brodskaya E.N. // Colloids Surf. A. 2014. V. 448. P. 175.
Копаничук И.В., Ванин А.А., Бродская Е.Н. // Коллоид. журн. 2015. Т. 77. С. 634.
Kopanichuk I.V., Vanin A.A., Brodskaya E.N. // Colloids Surf. A. 2017. V. 527. P. 42.
Irving J.H., Kirkwood J.G. // J. Chem. Phys. 1950. V. 18. P. 817.
Дополнительные материалы отсутствуют.
Инструменты
Коллоидный журнал