Коллоидный журнал, 2019, T. 81, № 1, стр. 101-114
Зародышеобразование конденсированной фазы в парах воды на наноструктурированной поверхности кристалла β-AgI. 2. Свободная энергия
С. В. Шевкунов *
Санкт-Петербургский политехнический университет Петра Великого
195251 Санкт-Петербург, ул. Политехническая, 29, Россия
* E-mail: shevk54@mail.ru
Поступила в редакцию 15.06.2018
Аннотация
Из первых принципов статистической механики методом биканонического статистического ансамбля рассчитаны свободная энергия и работа формирования из пара при температуре 260 и 400 K зародышей конденсированной фазы воды на наноструктурированной базовой грани кристалла йодистого серебра. Относительно крупные элементы структуры представляли собой регулярно повторяющиеся усеченные пирамиды размером 8 нм в основании и 3 нм высотой. Применена детализированная модель взаимодействий, включающая суммирование дальних электростатических и поляризационных взаимодействий с подложкой методом Эвальда. Зависимости свободной энергии и работы образования зародышей от их размеров сравниваются с соответствующими зависимостями для случая гладкой базовой грани кристалла. Наноструктурированность поверхности повышает на порядок величины термодинамическую устойчивость зародышей и “растягивает” на 5−6 порядков величины процесс их роста в область низких давлений. Относительно большие размеры элементов наноструктуры способствуют уменьшению свободной энергии поглощения молекул воды на начальной стадии зародышеобразования.
1. ВВЕДЕНИЕ
В термодинамике фазовых превращений гомогенной нуклеации до последнего времени уделялось гораздо больше внимания [1–14], чем гетерогенному зародышеобразованию [15–19], в том числе микроконденсации паров [20–23] и микрокристаллизации жидкостей [24–26] на твердых поверхностях. Еще меньше исследована гетерогенная нуклеация на поверхностях, содержащих дефекты [27–30], и в микропорах [31, 32], хотя, как правило, именно с такими поверхностями приходится иметь дело в случае твердых частиц, производимых в аэрозольных генераторах методом сублимации с последующим быстрым охлаждением [33].
Из-за относительно высоких барьеров свободной энергии на пути гомогенной нуклеации в естественных условиях зародышеобразование часто происходит гетерогенно. Гетерогенная нуклеация атмосферной влаги является промежуточным звеном, обеспечивающим влияние аэрозолей естественного и антропогенного происхождения на состояние воздушной среды, а также основным инструментом целенаправленных воздействий на атмосферные процессы [34].
Способность поверхностей влиять на образование зародышей конденсированной фазы не обязательно напрямую связана с их смачиваемостью. Наиболее активное из веществ, применяемых в качестве стимулятора конденсации водяного пара, йодистое серебро [35–37] относительно плохо смачивается водой. Смачиваемость определяется поверхностным натяжением на границе фаз и соответствующим ему углом смачивания. Эти характеристики имеют смысл только для достаточно крупных капель, в то время как началу зародышеобразования дают ядра наноскопических размеров.
Понятие свободной поверхностной энергии предполагает принципиальную возможность трактовать поверхностный слой как систему, к которой применимы понятия статистического ансамбля и равновесного распределения, в частности, понятия температуры и свободной энергии. В рамках строгого статистико-механического подхода для применимости к поверхностному слою понятия статистического ансамбля прямые взаимодействия молекул поверхностного слоя с внутренней областью капли должны быть исчезающе слабыми по сравнению с взаимодействиями внутри поверхностного слоя. Выполнение этого условия необходимо для того, чтобы система имела свой собственный спектр энергетических уровней, делающий возможным оперировать понятиями статистической суммы и свободной энергии [38].
Для выполнения указанных требований линейные размеры капли должны существенно превышать радиус межмолекулярных корреляций, который в жидкостях примерно на порядок больше молекулярных размеров. Оценки показывают, что капля в этом случае должна содержать не менее 106 молекул. Для капель меньшего размера разделение на поверхностный слой и внутреннюю область как самостоятельные термодинамические подсистемы, обладающие собственными термодинамическими характеристиками, строго говоря, невозможно. Кроме ограничений на размер капель трудности применения капиллярного приближения усугубляются еще и вариациями в их форме. Плоская форма зародыша, в виде молекулярной пленки толщиной, сравнимой или меньшей толщины переходного слоя, делает неприменимыми понятия поверхностной и объемной свободной энергии, а значит, поверхностного натяжения и угла смачивания. Для такого зародыша не ясно, какую форму имеет его поверхность и как на краю пленки располагается касательная к этой поверхности, задающая угол смачивания.
В случае крупных капель смачивание может сопровождаться долгоживущими метастабильными состояниями, не относящимися к равновесным. По всей видимости, к числу таких явлений следует отнести и состояние нерастекающейся капли воды на мономолекулярной подстилающей пленке, образовавшейся из пара на поверхности кристалла с гексагональной структурой, близкой к структуре базовой грани кристалла β-AgI. Это состояние, воспроизведенное методом молекулярной динамики в [39], сохраняло устойчивость в течение всего сеанса моделирования. К числу таких состояний, вероятно, следует отнести и некоторые из явлений, относящих к смачиванию по Касси–Бакстеру [40], при котором жидкость в контакте с твердой подложкой не проникает в микроскопические полости на ее поверхности. Капля в таком состоянии контактирует только с частью поверхности. Благодаря уменьшению площади контакта повышается свободная энергия на границе с подложкой, и капля ведет себя, как на сильно гидрофобной поверхности, не растекаясь и сохраняя компактную форму. Для перехода в равновесное состояние, связанное с проникновением в микропоры (смачивание по Венцелю [41]), капля должна была бы сначала увеличить площадь своей поверхности, повторив изрезанный рельеф подложки, что равносильно преодолению некоторого барьера свободной энергии.
С увеличением размеров капли барьеры, отделяющие метастабильные состояния от равновесных, возрастают, а относительные флуктуации уменьшаются. Вместе с ними экспоненциально резко, до макроскопических масштабов растет и время жизни таких состояний. В то же время в области наноскопических размеров барьеры, препятствующие росту зародышей, не достаточно высоки, чтобы обеспечить торможение нуклеации в макроскопических временны́х масштабах, и процесс будет развиваться по пути равновесных состояний. Стадия наноскопических размеров имеет здесь ключевое значение, так как именно для малых зародышей размерные эффекты в их термодинамическом поведении выражены наиболее сильно.
При интерпретации результатов, полученных для наноскопических зародышей, часто используются понятия, заимствованные из капиллярного приближения [42]. В [43] для исследования гетерогенной нуклеации на подложке с дефектом выполнено компьютерное моделирование для простейшей двумерной решеточной модели. Дефект моделировался в форме пятна, состоящего из поверхностного слоя переориентированных “спинов”. В поле дефекта наблюдалось гетерогенное образование зародышей конденсированной фазы, содержащих порядка 103 модельных частиц. Анализируя профиль кластеров, авторы используют понятие контактного угла, ссылаются на уравнение Юнга [44] и строят зависимости угла от параметра взаимодействия с внешним полем.
В [45] методом молекулярной динамики моделируется нанопузырек из примерно 104 леннард-джонсовских частиц, контактирующий с твердой поверхностью. Устойчивость системы анализируется в терминах свободной поверхностной энергии и угла смачивания.
В представленной работе методом компьютерного моделирования на молекулярном уровне, из первых принципов статистической механики выполнены расчеты свободной энергии и работы образования наноскопических зародышей конденсированной фазы воды на поверхности наиболее активного из известных стимуляторов конденсации переохлажденного пара – кристаллического йодистого серебра. На основе полученных зависимостей выявлены закономерности влияния наноструктурированности поверхности на стабильность и механизм роста конденсата, исследована устойчивость к вариациям температуры.
2. УСЛОВИЯ МОДЕЛИРОВАНИЯ
Расчеты выполнены методом Монте-Карло в биканоническом статистическом ансамбле (БСА) с применением периодических граничных условий [46]. Метод БСА [47–50] позволяет произвести вычисление свободной энергии и связанных с ней характеристик как функций количества молекул в области моделирования. Именно зависимости свободной энергии от размера системы определяют термодинамическую устойчивость зародышей и механизм их роста. В отличие от метода термодинамического интегрирования [51, 52], метода блуждания по температуре [53] и его модификаций [54–56], а также других непрямых методов расчета [57], в которых производится вычисление относительных значений, метод БСА является прямым методом, позволяющим получить абсолютные значения свободной энергии.
Условия моделирования совпадали с теми, которые описаны в предыдущей статье [58]. Зародыши конденсированной фазы воды росли в парах воды на базовой грани кристалла β-AgI. Наноструктура поверхности, как и в [58], представляла собой систему регулярным образом повторяющихся пирамид – по одной в каждой ячейке периодичности. Пирамиды имели высоту в 6 кристаллографических слоев и состояли из 3‑х слоев анионов йода размером 20 × 20, 16 × 16, 12 × 12 ионов и 3-х слоев катионов серебра таких же размеров.
Размер ячейки периодичности составлял 95.19 Å × 109.92 Å (24 × 24 иона). Область моделирования ограничивалась двумя параллельными плоскостями – одной на 3.5 Å ниже ионов первого кристаллографического слоя несущей поверхности под основанием пирамиды и другой на 10 Å выше ионов поверхностного кристаллографического слоя, находящегося на ее вершине. Сравнительные расчеты выполнены при температуре 260 и 400 K.
Применена модель межмолекулярных взаимодействий, описанная в предыдущей статье [58]. Дальние электростатические взаимодействия суммировались методом Эвальда [59–62]. Дополнительно методом Эвальда суммировались поляризационные взаимодействия с подложкой. Предыдущие расчеты показали [63, 64], что из-за высокой поляризуемости ионов йода в молекулярной пленке на поверхности йодистого серебра формируются домены. Доменообразование усиливает сцепление с подложкой и влияет на термодинамику зародышеобразования [65]. В этих условиях важно достаточно детально описать поляризационные взаимодействия. Численные значения параметров этой модели представлены в [66, 67].
Для расчета равновесных средних в каждом термодинамическом состоянии генерировались случайные последовательности молекулярных конфигураций длиной в 30 млн шагов, из которых первые 5 млн использовались для термализации и поиска оптимального значения химического потенциала виртуального термостата. Шаги по сдвигам молекул чередовались с соотношением частот 1 : 6 с попытками вбросить или удалить из области моделирования случайным образом выбранную молекулу [68]. Применялась процедура последовательного наращивания количества частиц в пределах ячейки периодичности от сеанса к сеансу моделирования. Максимальный сдвиг молекул на каждом шаге составлял 0.25 Å, а угол поворота 18°. Частота принятия новых конфигураций в попытках сдвинуть и повернуть молекулы менялась в пределах 50−60%, в попытках добавить или изъять молекулу – в пределах 0.01−0.1%. Шаги по вбрасыванию и удалению молекул, существенно ускоряют сходимость к равновесным средним в силу сопровождающих их хотя и редких, но кардинальных трансформаций молекулярных конфигураций.
3. ДЕТАЛИ ВЫЧИСЛИТЕЛЬНОЙ ПРОЦЕДУРЫ
3.1. Равновесное распределение
Расчет свободной энергии, энтальпии и энтропии присоединения молекул пара к адсорбированной компоненте выполнен методом БСА [47–50] с самонастраивающимся алгоритмом. В методе БСА совершаются попытки вбрасывания в случайную точку области моделирования и удаления случайно выбранной молекулы с вероятностями большого канонического статистического ансамбля [38]. Разрешены только состояния с n и n – 1 молекулами в системе. Вероятности разыгрываются с помощью генератора случайных чисел. Параллельно совершаются шаги по пространственным смещениям и поворотам молекул с переходными вероятностями канонического статистического ансамбля [68]. Частота присутствия конкретных конфигураций в полученной таким образом случайной последовательности микросостояний с n и n – 1 молекулами в ячейке периодичности определяется гиббсовской равновесной функцией распределения в конфигурационном пространстве $X(n)$
(1)
$\begin{gathered} \rho (n,X(n)){{d}^{n}}V{{d}^{n}}\Omega \sim \\ \sim \frac{1}{{n!}}{{(Z_{{{\text{tr}}}}^{{{\text{kin}}}})}^{n}}{{(Z_{{{\text{rot}}}}^{{{\text{kin}}}})}^{n}} \times \\ \times \,\,\exp \left( {[n\tilde {\mu } - {{U}_{n}}{{(X(n))]} \mathord{\left/ {\vphantom {{(X(n))]} {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}} \right){{d}^{n}}V{{d}^{n}}\Omega , \\ \end{gathered} $Выражение (1) для функции распределения в конфигурационном пространстве может быть переписано в форме, не зависящей от массы и моментов инерции молекул:
(2)
$\begin{gathered} \rho (n,X(n)){{d}^{n}}V{{d}^{n}}\Omega \sim \frac{1}{{n!}}{{(Z_{{{\text{tr}}}}^{{{\text{kin}}}})}^{n}}{{(Z_{{{\text{rot}}}}^{{{\text{kin}}}})}^{n}} \times \\ \times \,\,\exp \left( {[n\tilde {\mu } - {{{{U}_{n}}(X(n))]} \mathord{\left/ {\vphantom {{{{U}_{n}}(X(n))]} {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}} \right){{d}^{n}}V{{d}^{n}}\Omega = \\ = \frac{1}{{n!}}\text{v}_{{{\text{ref}}}}^{{ - n}}\exp \left( {\frac{{n{{{\tilde {\mu }}}^{{{\text{conf}}}}} - {{U}_{n}}(X(n))}}{{{{k}_{{\text{B}}}}T}}} \right){{d}^{n}}V{{d}^{n}}\Omega , \\ \end{gathered} $3.2. Переходные вероятности
Распределение (2) получается как предельное распределение в марковском случайном процессе блужданий в пространстве молекулярных конфигураций с числами молекул n и n – 1. Процесс моделируется численно на компьютере и направляется переходными вероятностями ${{p}_{{ij}}},$ удовлетворяющими условию детального баланса. В частности, переходы между микросостояниями, которые различаются количеством молекул, $i:(n - 1,X(n - 1))$ и $j:(n,X(n)),$ совершаются с вероятностями, удовлетворяющими соотношению
(3)
$\begin{gathered} \frac{{{{p}_{{ij}}}}}{{{{p}_{{ji}}}}} = \frac{{{{\rho }_{j}}}}{{{{\rho }_{i}}}} = \frac{1}{n} \times \\ \times \,\,\exp \left( {\frac{{{{{\tilde {\mu }}}^{{{\text{conf}}}}} - ({{U}_{n}}({{X}_{n}}) - {{U}_{{n - 1}}}({{X}_{{n - 1}}}))}}{{{{k}_{{\text{B}}}}T}}} \right)\text{v}_{{{\text{ref}}}}^{{ - 1}}dVd\Omega = \\ = \frac{{d\Omega }}{{\left( {\frac{{8{{\pi }^{2}}}}{\gamma }} \right)}}\frac{{dV}}{V}\frac{V}{n}\text{v}_{{{\text{ref}}}}^{{ - {\text{1}}}}\exp \left( {\frac{{{{{\tilde {\mu }}}^{{\text{c}}}} - ({{U}_{n}}({{X}_{n}})) - {{U}_{{n - 1}}}({{X}_{{n - 1}}}))}}{{{{k}_{{\text{B}}}}T}}} \right), \\ \end{gathered} $3.3. Вычисление химического потенциала
В силу соотношения $\mu = \frac{{\partial F(n,V,T)}}{{\partial n}}$ искомое значение химического потенциала молекул в системе получается как разность свободных энергий в состояниях с $n$ и $n - 1$ молекулами и выражается через отношение соответствующих статистических сумм:
В свою очередь, в большом каноническом статистическом ансамбле вероятность $w(n)$ обнаружить систему в состоянии с количеством молекул n пропорциональна $Q(n,V,T)\exp \left( {{{\tilde {\mu }} \mathord{\left/ {\vphantom {{\tilde {\mu }} {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}} \right)$ [38]. Поэтому химический потенциал молекул в системе может быть рассчитан через это отношение согласно формуле
(4)
${{\mu }_{{{\text{cl}}}}}(n,V,T) = \tilde {\mu } - {{k}_{{\text{B}}}}T\ln \left( {\frac{{w(n)}}{{w(n - 1)}}} \right).$Отношение вероятностей под логарифмом в правой части (4) рассчитывается численно путем прямого подсчета соответствующих количеств микросостояний в генерируемой случайной последовательности конфигураций, а значение химического потенциала термостата $\tilde {\mu }$ задается в качестве входного параметра расчетов.
3.4. Самонастраивающийся алгоритм
Хотя $\tilde {\mu }$ входит в правую часть (4), значение ${{\mu }_{{{\text{cl}}}}}(n,V,T)$ фактически не зависит от задаваемой величины $\tilde {\mu }.$ Вариации $\tilde {\mu }$ сопровождаются соответствующими компенсирующими вариациями величины выражения под логарифмом так, что правая часть (4) остается неизменной. В то же время, расчеты в конечных случайных выборках всегда сопровождаются некоторой статистической погрешностью, зависящей от объема выборки. Минимальная абсолютная погрешность рассчитываемой величины логарифма в правой части (4) достигается в режиме, когда $w(n) = $ = $w(n - 1),$ то есть, когда задаваемая величина параметра $\tilde {\mu }$ совпадает со значением ${{\mu }_{{{\text{cl}}}}}(n,V,T),$ которое, однако, заранее неизвестно. Из-за экспоненциально резкой зависимости вероятностей $w(n)$ от задаваемой величины $\tilde {\mu }$ практически невозможно угадать ее оптимальное значение, а попытки расчетов с далекими от оптимальных значениями $\tilde {\mu }$ заканчиваются неудачей – система “сваливается” в одно из состояний с количеством молекул n или n – 1, переходы между ними не происходят, и необходимый объем статистики для расчета отношения вероятностей ${{w(n)} \mathord{\left/ {\vphantom {{w(n)} {w(n - 1)}}} \right. \kern-0em} {w(n - 1)}}$ накопить не удается.
Проблема решается методом последовательных приближений. Для этого в расчетном алгоритме предусмотрен режим самонастройки, работающий по принципу обратной связи: компьютерная программа генерирует последовательность молекулярных конфигураций в соответствии с (3), одновременно корректируя величину $\tilde {\mu }$ в нужную сторону так, чтобы максимально приблизиться к режиму с равными частотами посещений состояний с $n$ и $n - 1$ молекулами.
Коррекция осуществляется на основании статистических данных, накопленных на предыдущих шагах случайного процесса. Эти данные заносятся в счетчик с весовыми коэффициентами, которые последовательно нарастают так, что получаемые последние данные имеют более высокий приоритет, по сравнению с устаревающими более ранними данными. В качестве весового коэффициента использовался номер шага случайного процесса в некоторой задаваемой фиксированной степени $\alpha > 0,$ определяющей функцию памяти со значением на M-ом шаге, равным $\psi (M) = {{\left( {\sum\nolimits_{k = 1}^M {{{{({{\xi }_{k}})}}^{\alpha }}} } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\nolimits_{k = 1}^M {{{{({{\xi }_{k}})}}^{\alpha }}} } \right)} {\left( {\sum\nolimits_{k = 1}^M {{{k}^{\alpha }}} } \right) - 0.5}}} \right. \kern-0em} {\left( {\sum\nolimits_{k = 1}^M {{{k}^{\alpha }}} } \right) - 0.5}},$ где ${{\xi }_{k}} = k,$ если на k-ом шаге система оказалась в состоянии с $n$ молекулами, и ${{\xi }_{k}} = 0,$ если в состоянии с $n - 1$ молекулами. Коррекция химического потенциала термостата производилась через каждые $\Delta {\kern 1pt} M$ шагов и состояла в умножении $\tilde {\mu }$ на $(1 - \varepsilon \psi (M))$. Темп коррекции $\tilde {\mu },$ определяемый задаваемыми величинами $\varepsilon > 0$ и $\Delta M,$ а также темп демпфирования устаревающих данных в функции памяти, определяемый величиной $\alpha $, устанавливались такими, чтобы, с одной стороны, релаксация к оптимальному значению $\tilde {\mu }$ происходила достаточно быстро, но, с другой стороны, алгоритм оставался устойчивым к явлениям самовозбуждения, характерным для систем с обратными связями. По окончанию режима коррекции величина $\tilde {\mu }$ фиксировалась.
Описанный алгоритм представляет собой расчет химического потенциала в два этапа в соответствии с двумя слагаемыми, входящими в правую часть (4): слагаемое $\tilde {\mu }$ является оценкой величины химического потенциала в первом приближении и рассчитывается методом итераций, второе, логарифмическое слагаемое представляет собой уточнение искомой величины ${{\mu }_{{{\text{cl}}}}}(n,V,T)$ и рассчитывается на заключительном этапе, после фиксации величины $\tilde {\mu }.$
3.5. Оптимизация режима термализации
Для анализа термодинамической устойчивости ключевое значение имеют зависимости от количества молекул в системе. Численные значения химического потенциала рассчитывались для заданной последовательности значений $n$ с нарастающим шагом, а затем интерполировались кубическими сплайнами, чтобы получить соответствующие значения с единичным шагом по $n$, которые использовались для численного интегрирования и расчетов сопряженных термодинамических характеристик. Все вычисления, связанные с интерполяцией и обработкой равновесных средних, были заранее запрограммированы и выполнялись в автоматическом режиме.
Расчет равновесных средних производился после достижения стационарного режима. Для этого начальный сегмент марковской траектории исключался из расчетов равновесных средних. Для ускорения термализации использовался алгоритм последовательного наращивания размеров системы, в котором начальная конфигурация для расчетов равновесных средних со следующим значением $n$ получалась добавлением необходимого количества молекул в последнюю конфигурацию, полученную при расчетах с предыдущим $n$. Добавление производилось вбрасыванием молекул из термостата в случайную точку области моделирования в соответствии с равновесной функцией распределения большого канонического статистического ансамбля с последующей термализацией. На термализацию и отработку оптимального значения $\tilde {\mu }$ отводилось 10 млн марковских шагов. Столько же шагов использовалось для расчета равновесных средних и отношения $\frac{{w(n)}}{{w(n - 1)}}$ в выражении для химического потенциала в правой части (4).
3.6. Вычисление свободной энергии
В расчетах с фиксированным объемом системы $V$ численным суммированием рассчитанных и интерполированных значений химического потенциала получается свободная энергия Гельмгольца
(5)
$F(N,V,T) = \sum\limits_{n = 1}^{n = N} {\left( {\tilde {\mu } - {{k}_{{\text{B}}}}T\ln \left( {\frac{{w(n)}}{{w(n - 1)}}} \right)} \right)} ,$(6)
$G(N,p,T) = \sum\limits_{n = 1}^{n = N} {\left( {\tilde {\mu } - {{k}_{{\text{B}}}}T\ln \left( {\frac{{w(n)}}{{w(n - 1)}}} \right)} \right)} .$При достаточно низком давлении пара (${{p{{V}_{{{\text{cl}}}}}} \mathord{\left/ {\vphantom {{p{{V}_{{{\text{cl}}}}}} {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}} \ll 1,$ где ${{V}_{{{\text{cl}}}}}$ – объем, фактически занимаемый адсорбированной компонентой в пределах ячейки периодичности) свободная энергия системы в объеме $V$ практически совпадает со свободной энергией адсорбированной компоненты, $F(N,V,T) = $ ${{F}_{{{\text{cl}}}}}(N,T),$ и зависимостью энергии Гиббса от давления можно пренебречь: $G(N,p,T) = $ ${{G}_{{{\text{cl}}}}}(N,T).$ Зависимостью от давления и объема области моделирования можно пренебречь и для всех других термодинамических характеристик, включая и химический потенциал ${{\mu }_{{{\text{cl}}}}}(n,V,T) \approx $ ${{\mu }_{{{\text{cl}}}}}(n,T).$ В этих условиях разницей между свободной энергией Гельмгольца и энергией Гиббса тоже можно пренебречь: ${{F}_{{{\text{cl}}}}}(N,T) \approx $ ≈ ${{G}_{{{\text{cl}}}}}(N,T).$ Энтропия рассчитывается через разность между внутренней энергией и свободной энергией $S(N,T)$ $ = (U(N,T)$ $ - \,\,F{{(N,T))} \mathord{\left/ {\vphantom {{(N,T))} T}} \right. \kern-0em} T}$ или как разность энтальпии и энергии Гиббса $S(N,T) = $ = $(H(N,T) - $ $G{{(N,T))} \mathord{\left/ {\vphantom {{(N,T))} T}} \right. \kern-0em} T}.$
Для сопоставления с получаемыми в натурном эксперименте данными удобно выразить рассчитанные термодинамические характеристики в терминах давления пара над подложкой. Давление пара, находящегося в равновесии с адсорбированной компонентой, может быть найдено из условия равенства их химических потенциалов, $\mu (p,T)$ $ = {{\mu }_{{{\text{cl}}}}}(n,T)$ в приближении идеального газа для пара:
(7)
$p = \frac{{{{k}_{{\text{B}}}}T}}{{{{\text{v}}_{{{\text{ref}}}}}}}\exp (\mu _{{{\text{cl}}}}^{{\text{c}}}{{(n,T)} \mathord{\left/ {\vphantom {{(n,T)} {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}),$4. РЕЗУЛЬТАТЫ КОМПЬЮТЕРНЫХ РАСЧЕТОВ
Энергия Гиббса поглощения молекулы пара адсорбирующей поверхностью равна изменению энергии Гиббса объединенной системы “адсорбированная компонента + пар” и складывается из изменения энергии Гиббса адсорбированной компоненты за счет увеличения ее размеров на одну молекулу, $\Delta {{G}_{{{\text{cl}}}}}(N,T)$ $ = \frac{{\partial {{G}_{{{\text{cl}}}}}(N,T)}}{{\partial N}}$ $ = {{\mu }_{{{\text{cl}}}}}(N,T),$ и изменения энергии Гиббса пара за счет изъятия из него одной молекулы, равного
(8)
$\begin{gathered} \Delta G(N,p,T) = \Delta {{G}_{{{\text{cl}}}}}(N,T) - \mu (p,T) = \\ = {{\mu }_{{{\text{cl}}}}}(N,T) - \mu (p,T), \\ \end{gathered} $Расчет ${{\mu }_{{{\text{cl}}}}}(N,T)$ выполнялся в соответствии с соотношением (4) методом Монте-Карло в БСА, а для химического потенциала молекул пара применялась формула идеального газа жестких ротаторов $\mu (p,T) = $ $ - {{k}_{{\text{B}}}}T\ln \left( {\frac{{8{{\pi }^{2}}{{k}_{{\text{B}}}}T}}{{\gamma p}}Z_{{{\text{tr}}}}^{{{\text{kin}}}}Z_{{{\text{rot}}}}^{{{\text{kin}}}}} \right),$ которая для конфигурационной части химического потенциала, относящейся к трансляционному движению, принимает вид ${{\mu }^{{\text{с }}}}(p,T) = $ ${{k}_{{\text{B}}}}T\ln \left( {\frac{{p{{\text{v}}_{{{\text{ref}}}}}}}{{{{k}_{{\text{B}}}}T}}} \right).$ Выражение (8) в терминах трансляционных компонент конфигурационных частей химического потенциала записывается как $\Delta G(N,p,T) = $ = $\mu _{{{\text{cl}}}}^{{\text{c}}}(N,T) - {{\mu }^{{\text{c}}}}(p,T),$ из которого следует, что энергия Гиббса поглощения молекулы не зависит от ее массы и моментов инерции, а зависимость ее от давления пара носит тривиальный характер: пересчет значений энергии Гиббса поглощения от стандартного давления ${{p}_{0}}$ к любому другому его значению $p$ может быть произведен по формуле $\Delta G(N,p,T) = $ $\Delta G(N,{{p}_{0}},T) - {{k}_{{\text{B}}}}T\ln \left( {{p \mathord{\left/ {\vphantom {p {{{p}_{0}}}}} \right. \kern-0em} {{{p}_{0}}}}} \right).$ С увеличением давления кривая зависимости $\Delta G(N,p,T)$ как функции $N$ смещается вниз вдоль оси ординат параллельно самой себе без изменения формы. Форма этой кривой является универсальной характеристикой адсорбата, не зависящей от давления пара над поверхностью, а величина $\Delta G(N,p,T)$ лежит в основе всех термодинамических характеристик процесса поглощения и зародышеобразования на поверхности.
Данные, приведенные на рис. 1, свидетельствуют о том, что термодинамика поглощения молекул пара на наноструктурированной поверхности кардинально отличается от таковой на гладкой поверхности. С увеличением количества адсорбированных молекул темп, с которым растет энергия Гиббса присоединения на наноструктурированной поверхности (кривая 2), на порядки выше, чем на гладкой поверхности (кривая 1). Ускоренный рост энергии Гиббса отражает быстро изменяющиеся условия захвата молекул на наноструктурированной поверхности. На гладкой поверхности каждая новая захваченная молекула пара присоединяется к краю растущей мономолекулярной пленки. Условия присоединения таких молекул почти не изменяются с ростом пленки, поэтому не изменяется и энергия присоединения.
Рис. 1.
Энергия Гиббса поглощения одной молекулы водяного пара при температуре 260 K в расчете на стандартное давление пара в 1 атм базовой гранью кристалла β-AgI как функция количества молекул воды, удерживаемых на поверхности в пределах ячейки периодичности; 1 − гладкая грань с ионами серебра в поверхностном кристаллографическом слое, 2 − та же грань с регулярной наноструктурой в виде повторяющихся с периодом 95.19 Å × 109.92 Å пирамид высотой в шесть кристаллографических слоев.
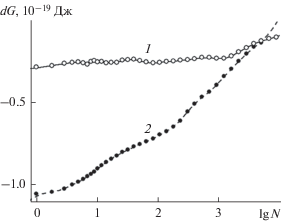
На наноструктурированной поверхности захват молекул происходит, прежде всего, на террасах пирамид. Захват молекул в местах, наиболее благоприятных для присоединения, сопровождается существенным понижением энергии системы, однако емкость таких областей невелика, и они быстро заполняются молекулами, оставляя свободными менее энергетически выгодные области. Присоединение молекул пара к оставшимся свободными фрагментам поверхности не вызывает столь же сильного уменьшения энергии, что является причиной быстрого роста $\Delta G(N,p,T)$ в случае наноструктурированной поверхности. Быстрый рост $\Delta G(N,p,T)$ означает повышенную термодинамическую устойчивость системы. Действительно, с учетом дискретности переменной $N$ и равенства (8)
(9)
$\begin{gathered} \frac{{\partial \Delta G(N,p,T)}}{{\partial N}} = \frac{{\partial {{\mu }_{{{\text{cl}}}}}(N,T)}}{{\partial N}} = \\ = \frac{{{{\partial }^{2}}{{G}_{{{\text{cl}}}}}(N,T)}}{{\partial {{N}^{2}}}} = \frac{{{{\partial }^{2}}A(N,p,T)}}{{\partial {{N}^{2}}}}, \\ \end{gathered} $На рис. 2а представлены зависимости удельных внутренней (кривые 1, 3) и свободной энергий (кривые 2, 4) зародышей конденсированной фазы на гладкой (кривые 1, 2) и наноструктурированной (кривые 3, 4) поверхностях от количества адсорбированных молекул. Вариации энергии в процессе адсорбции отражают изменение условий присоединения молекул пара к зародышу. В частности, нисходящая часть в начале кривой 2 на рис. 2а отражает рост размеров пятен мономолекулярной пленки, сопровождающийся уменьшением относительной доли молекул, находящихся на краях пятен и поэтому обладающих более высокой энергией. На кривой свободной энергии 1 это уменьшение компенсировано падением энтропии (кривая 1 на рис. 3а), и кривая 1 проходит полого.
Рис. 2.
Свободная (1, 3) и внутренняя (2, 4) энергия (включая кинетическую) конденсата, адсорбированного на базовой грани кристалла β-AgI, в расчете на одну молекулу воды в тех же условиях гладкой (1, 2) и наноструктурированной (3, 4) поверхностей, что и на рис. 1, при температуре 260 (а) и 400 K (б).
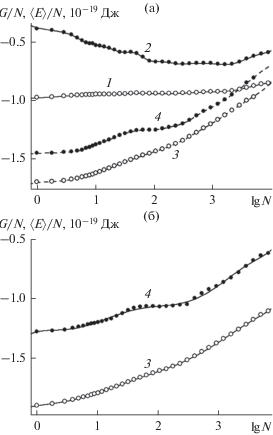
Рис. 3.
Энтропия конденсата, адсорбированного на базовой грани кристалла β-AgI, в расчете на одну молекулу в тех же условиях гладкой (1) и наноструктурированной (2) поверхностей, что и на рис. 1, при температуре 260 K в широком диапазоне поверхностной плотности молекул (а) и в области экстремально низких значений плотности (б).
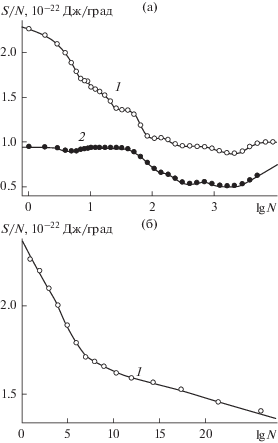
На наноструктурированной поверхности внутренняя энергия изменяется в противоположную сторону (кривая 4). Ее рост, вместо падения, указывает на качественно иной механизм адсорбции. Рост энергии обусловлен здесь последовательным уменьшением количества мест, наиболее благоприятных для присоединения молекул. При этом энтропия в расчете на одну молекулу на этой стадии остается неизменной (кривая 2 на рис. 3а), так как молекулы присоединяются к поверхности по отдельности, без образования межмолекулярных связей.
Различия в механизмах роста зародышей на гладкой и наноструктурированной поверхностях отражаются в поведении энтропии и в самом начале адсорбции: форма кривой на рис. 3б отчетливо демонстрирует переход от быстрого падения удельной энтропии к более пологому ее ходу при $N > 6.$ Размер $N = 6$ отвечает шестизвенному молекулярному циклу, а резкое падение энтропии, которое сопровождает его формирование, является отражением относительной жесткости этой конструкции. В случае наноструктурированной поверхности пологий ход удельной энтропии не позволяет идентифицировать шестизвенные циклы (кривая 2 на рис. 3а), что согласуется с наблюдавшимся в [58] качественно иным механизмом зародышеобразования.
Кривые свободной энергии на рис. 2а – более гладкие из-за наличия в свободной энергии $E - TS$ энтропийной составляющей $ - TS$, которая частично сглаживает колебания внутренней энергии $E$: более глубокие потенциальные ямы на адсорбирующей поверхности, как правило, бывают и более узкими. Как следствие, низкие значения энергии сопровождаются и более низкими значениями энтропии. Поэтому вариации, связанные с различными режимами роста зародышей, сильнее выражены в поведении внутренней, чем свободной энергии. Одна из таких особенностей в виде замедления роста кривой 4 в районе $N \approx {{10}^{2}}$ связана с завершением этапа заполнения наиболее благоприятных точек присоединения молекул на боковых гранях пирамиды. Эта особенность воспроизводится и при более высокой температуре, на рис. 2б.
Термодинамическая устойчивость зародышей конденсированной фазы на поверхности кристалла определяется формой кривой работы образования $A(N,p,T).$ Минимумы на этой зависимости $\left( {\frac{{{{\partial }^{2}}A(N,p,T)}}{{\partial {{N}^{2}}}} > 0} \right)$ отвечают состояниям устойчивого равновесия с паром, а максимумы $\left( {\frac{{{{\partial }^{2}}A(N,p,T)}}{{\partial {{N}^{2}}}} < 0} \right)$ представляют неустойчивые равновесные состояния. В условиях термических флуктуаций система самопроизвольно переходит в одно из устойчивых состояний, при этом возможно лавинообразное испарение или конденсационный рост до макроскопических размеров. Локальные минимумы на зависимости $A(N,p,T),$ разделенные барьерами, отвечают метастабильным состояниям, время жизни которых зависит от высоты и ширины барьеров.
На рис. 4 и 5 представлены зависимости работы образования зародышей от N, полученные в сравнительных расчетах для гладкой и наноструктурированной поверхности соответственно. Если на гладкой поверхности состояния неустойчивости возможны (максимумы в точке $\lg (N) = 1.7$ на рис. 4а и в точке $\lg (N) = 2.9$ на рис. 4б), то на наноструктурированной поверхности они отсутствуют полностью – все кривые на рис. 5 − вогнутые, с глубокими минимумами как в области низких, (рис. 5а), так и высоких (рис. 5б) давлений пара над поверхностью. Минимумы в случае наноструктурированной поверхности имеют на порядок бóльшую глубину (сравните масштабы на осях ординат на рис. 4 и 5), и устойчивость зародышей выше.
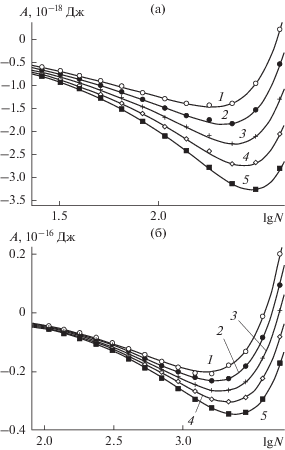
Рис. 4.
Работа формирования конденсата из паров воды при 260 K на базовой грани кристалла β-AgI в отсутствие поверхностных дефектов в расчете на одну ячейку периодичности размером 126.92 Å × 146.56 Å как функция количества молекул, адсорбированных в пределах ячейки периодичности, в областях малой (а) и умеренной (б) поверхностной плотности молекул. Зависимости получены для следующих значений давления пара над поверхностью: 1 – 27.6, 2 – 32.8, 3 – 39.0 Па (а) и 1 – 65.5, 2 – 78.0, 3 – 92.7 Па (б).
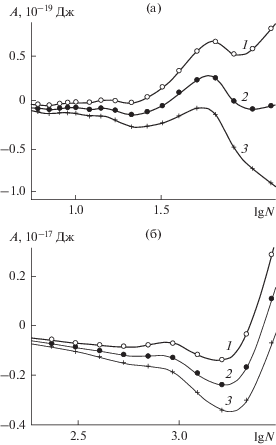
Рис. 5.
То же, что на рис. 4, на наноструктурированной базовой грани кристалла β-AgI в областях малой (а) и умеренной (б) поверхностной плотности молекул. Зависимости получены при 260 K для следующих значений давления пара: 1 – 10–3, 2 – 1.68 × 10–3, 3 – 2.82 × 10–3, 4 – 4.76 × 10–3, 5 – 8 × 10–3 Па (а) и 1 – 6.89, 2 – 11.6, 3 – 19.5, 4 – 32.8, 5 – 55.1 Па (б).
Данные, полученные для равновесной работы образования зародышей, подтверждают рост их устойчивости за счет наноструктурированности поверхности – глубина соответствующих минимумов на зависимостях работы образования увеличивается на порядок. Зародыши на наноструктурированной поверхности сохраняют повышенную устойчивость и при значениях температуры выше точки кипения воды, хотя соответствующие размеры зародышей достигаются при более высоких давлениях пара, рис. 6.
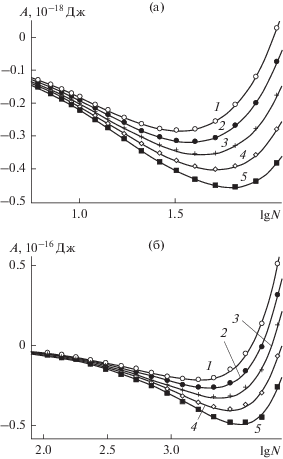
Рис. 6.
То же, что на рис. 5, при температуре 400 K для следующих значений давления пара: 1 – 3.44, 2 – 4.10, 3 – 4.87, 4 – 5.79, 5 – 6.89 Па (а) и 1 – 28.2, 2 – 47.4, 3 – 79.8, 4 – 134, 5 – 226 кПа (б).
Компактной количественной характеристикой, позволяющей судить о термодинамической устойчивости зародышей, является работа образования из пара, находящегося в равновесии с зародышем:
Выражение (11) получается из (10) подстановкой в него условия материального равновесия с паром $\mu (p,T) = $ ${{\mu }_{{{\text{cl}}}}}(N,T).$ Дифференцирование (11) по $N$ с учетом тождества ${{\mu }_{{{\text{cl}}}}}(N,T)$ $ = \frac{{\partial {{G}_{{{\text{cl}}}}}(N,T)}}{{\partial N}}$ дает
(12)
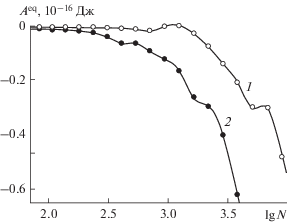
$\frac{{\partial {{A}^{{{\text{eq}}}}}(N,T)}}{{\partial N}} = - N\frac{{{{\partial }^{2}}A(N,p,T)}}{{\partial {{N}^{2}}}}.$На рис. 7 представлены результаты сравнительных расчетов ${{A}^{{{\text{eq}}}}}(N,T)$ на гладкой и наноструктурированной поверхностях. Как можно заключить из представленных зависимостей, наноструктурированность поверхности приводит к существенному повышению устойчивости зародышей. Зависимости ${{A}^{{{\text{eq}}}}}(N,T)$ от количества адсорбированных молекул $N$ позволяют разглядеть эффекты, которые не видны на семействе кривых $A(N,p,T).$ В частности, на кривых ${{A}^{{{\text{eq}}}}}(N,T)$ рис. 7 видны “всплески”, которые отмечают завершение очередной стадии формирования зародыша. Если на гладкой поверхности каждая такая стадия связана с заполнением очередного мономолекулярного слоя, то на наноструктурированной поверхности пространственная организация зародышей слишком сложна, чтобы по их внешнему виду идентифицировать различные стадии роста. Можно только констатировать, что и на наноструктурированной поверхности в формировании зародышей различаются стадии, влияющие на термодинамическое поведение системы.
Рис. 7.
Работа адсорбции на гладкой (1) и наноструктурированной (2) базовой грани кристалла β-AgI паров воды с плотностью, отвечающей материальному равновесию с адсорбатом при температуре 260 K, как функция количества адсорбированных молекул в пределах ячейки периодичности.
Наиболее вероятной причиной стадийного роста зародышей на наноструктурированной поверхности является последовательное заполнение различных граней поверхностных дефектов – сначала адсорбция происходит на краях террас, затем распространяется на сами террасы и только после этого на верхнюю площадку пирамид и несущую поверхность у их подножья [58]. Хотя, как видно из представленных зависимостей, структура поверхности может влиять на адсорбционные кривые, для выявления этого влияния необходимо привлекать достаточно чувствительные критерии и прецизионные измерения.
Наличие различных стадий роста является следствием относительно больших пространственных размеров элементов наноструктуры. При таких размерах можно наблюдать раздельную адсорбцию на частях этих элементов. Характерным размером элементов шероховатости, достаточным для раздельной адсорбции на их различных гранях, следует считать значение, существенно превышающее радиус межмолекулярных корреляций в жидкой воде, что соответствует масштабам от нескольких до нескольких десятков нанометров. Таким образом, пространственные размеры дефектов, которые моделируются в представленном исследовании, отвечают границе режима раздельной адсорбции. Для аналитических расчетов эта область размеров представляет наибольшие трудности.
Изотермы адсорбции – количества конденсированного вещества, удерживаемого на поверхности в зависимости от давления пара над ней, представляют особый интерес. Изотермы адсорбции технически проще измерить в реальном лабораторном эксперименте, чем такие характеристики, как работа образования или энтропия, и именно они, как правило, анализируются в первую очередь.
Количество молекул ${{N}_{{\text{s}}}}$ в термодинамически устойчивом зародыше конденсированной фазы на поверхности соответствует положению минимумов на зависимостях работы образования на рис. 4−6. С увеличением давления минимумы смещаются вправо, в сторону бóльших размеров. Согласно термодинамическому тождеству для равновесных размеров ${{N}_{{\text{s}}}}$ [69–72]
(13)
$\frac{{\partial {{N}_{{\text{s}}}}}}{{\partial p}} = \frac{{{{k}_{{\text{B}}}}T}}{p}{{\left( {\frac{{{{\partial }^{2}}{{G}_{{{\text{cl}}}}}(n,T)}}{{\partial {{N}^{2}}}}\begin{array}{*{20}{c}} | \\ | \\ | \end{array}\begin{array}{*{20}{c}} {} \\ {} \\ {_{{N = {{N}_{{\text{s}}}}}}} \end{array}} \right)}^{{ - 1}}},$Комбинируя (13) с (12), с учетом последнего равенства (9), получаем
(14)
$\frac{{\partial \ln ({{N}_{{\text{s}}}})}}{{\partial \ln p}} = - {{k}_{{\text{B}}}}T{{\left( {\frac{{\partial {{A}^{{{\text{eq}}}}}(N,T)}}{{\partial N}}\begin{array}{*{20}{c}} | \\ | \\ | \end{array}\begin{array}{*{20}{c}} {} \\ {} \\ {_{{N = {{N}_{{\text{s}}}}}}} \end{array}} \right)}^{{ - 1}}}.$Из (14) следует, что в области спада зависимости ${{A}^{{{\text{eq}}}}}(N,T)$ размер зародыша ${{N}_{{\text{s}}}}$ растет с давлением пара, и такой ход ${{N}_{{\text{s}}}}$, согласно (12), указывает на устойчивость. Наоборот, рост ${{A}^{{{\text{eq}}}}}(N,T)$ однозначно связан с убывающим размером ${{N}_{{\text{s}}}}$ и неустойчивостью зародыша.
В общем случае проинтегрировать уравнение (14) аналитически не удается, так как результат зависит от вида функции ${{A}^{{{\text{eq}}}}}(N,T),$ однако качественный анализ решения можно выполнить на примере простейшего случая линейной зависимости ${{A}^{{{\text{eq}}}}}(N,T).$ В случае устойчивого равновесия эта производная представляет собой константу с отрицательным знаком $\frac{{\partial {{A}^{{{\text{eq}}}}}(N,T)}}{{\partial N}} \equiv - C,$ $C > 0,$ и уравнение может быть проинтегрировано:
(15)
${{N}_{{\text{s}}}} \propto {{p}^{{{{k}_{{\text{B}}}}{T \mathord{\left/ {\vphantom {T C}} \right. \kern-0em} C}}}}.$Из (15) видно, что в нулевом приближении размер зародыша зависит от давления в форме степенной функции, причем чем сильнее наклон спадающей кривой ${{A}^{{{\text{eq}}}}}(N,T)$ (больше величина $С $), тем более полога кривая ${{N}_{{\text{s}}}}(p).$
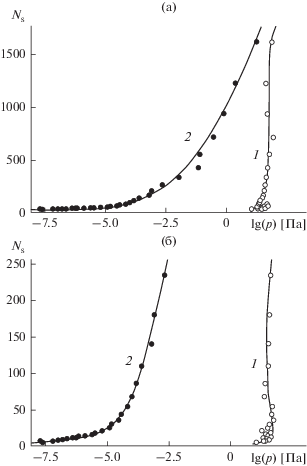
На рис. 8 представлены полученные компьютерным моделированием зависимости ${{N}_{{\text{s}}}}$ от давления для случаев гладкой и наноструктурированной поверхностей. В соответствии с указанными общими закономерностями рост ${{N}_{{\text{s}}}}$ в условиях гладкой поверхности (кривая 1) оказывается гораздо более резким, чем на наноструктурированной поверхности (кривая 2). В случае наноструктурированной поверхности кривая сильно вытянута в область низких давлений – захват молекул пара начинается при давлениях, на 5−6 порядков более низких, чем на гладкой поверхности. Это наблюдение согласуется с более крутым ходом кривой 2 по сравнению с кривой 1 на рис. 7. Кривые на рис. 8 сильно различаются по форме из-за экспоненциально резкой, как это следует из (15), зависимости их хода от величины $\frac{{\partial {{A}^{{{\text{eq}}}}}(N,T)}}{{\partial N}}.$
Рис. 8.
Равновесные размеры зародыша конденсированной фазы (количество молекул в расчете на ячейку периодичности), формирующегося на гладкой (1) и наноструктурированной (2) базовой грани кристалла β-AgI при разном давлении паров воды и температуре 260 К; (а) широкая область размеров, (б) начальная стадия.
Полученные компьютерным моделированием функциональные зависимости, находясь в согласии с общими термодинамическими соотношениями, указывают на особенности, обусловленные структурой подложки. Наноструктурированность поверхности влечет резкое усиление ее поглощательной способности в области экстремально низких давлений. Формирование зародыша растягивается и начинается задолго до того, как на гладкой поверхности становится возможным удержать даже небольшое количество молекул. Качественное объяснение этого явления состоит в возможности структурированной поверхности удерживать отдельные молекулы за счет их прямых взаимодействий с ионами кристаллической решетки подложки, в то время как на гладкой поверхности определяющую роль играют коллективные эффекты – взаимодействия между захваченными молекулами и определенный порядок их взаимного расположения.
ЗАКЛЮЧЕНИЕ
Компьютерное моделирование зародышеобразования на поверхности кристалла йодистого серебра с детальным описанием межмолекулярных сил, вычислением свободной энергии и работы образования показало, что увеличение характерных пространственных размеров элементов наноструктуры поверхности качественно меняет характер ее взаимодействия с неупорядоченной фазой. В отличие от мелкомасштабных наноструктур, в условиях наличия крупных элементов рост зародышей конденсированной фазы на различных гранях структурных элементов начинается при разных значениях давления пара и развивается раздельно. Грани, представляющие наиболее благоприятные условия для адсорбции, поглощают молекулы пара при давлениях, на несколько порядков более низких, чем это имеет место на гладкой поверхности. Растущие на них зародыши постепенно покрывают соседние, менее благоприятные области. Такой сценарий приводит к сильному растягиванию зародышеобразования в область низких давлений пара.
Наноструктура поверхности с характерными размерами, превышающими радиус межмолекулярных корреляций, существенно повышает термодинамическую устойчивость зародышей к испарению и связывает заметное количество паров воды даже в условиях экстремально сухой воздушной среды. Вместе с увеличением или уменьшением плотности пара над поверхностью зародыши обратимым образом растут или уменьшаются, без образования метастабильных состояний и гистерезиса. Эффект устойчив к вариациям температуры и остается столь же выраженным при значениях температуры выше точки кипения воды.
Исходя из данных, полученных для конкретного кристалла, было бы преждевременно утверждать, что указанные закономерности относятся ко всем типам кристаллических поверхностей. По всей видимости, они справедливы для гидрофильных поверхностей, а в случае поверхностей с выраженными гидрофобными свойствами наноструктурированность может не оказывать на зародыши стабилизирующего эффекта. Кроме того, следует учесть, что некоторые состояния, такие как не растекающаяся по поверхности капля макроскопических размеров, могут быть не равновесными, а долгоживущими метастабильными состояниями, существующими благодаря специальному способу их получения. Проникновению жидкости в поры мешает поверхностное натяжение, для существования которого капля должна обладать достаточно большими размерами. При последовательном росте зародыша из пара, включающем стадию наноскопических размеров, такие состояния могут не достигаться, а конденсат проникнет в наноскопические поры уже на начальной стадии зародышеобразования.
Работа выполнена при поддержке Министерства образования и науки РФ (проект № 3.4808.2017/6.7) и Российского фонда фундаментальных исследований (проект № 18-03-00011).
Список литературы
Volmer M., Weber A. // Z. phys. Chemie. 1926. V. 119. P. 277.
Becker R., Döring W. // Ann. Phys. 1935. V. 24. P. 719.
Volmer M. Kinetik der Phasenbildung. Leipzig: T. Steinkopff, 1939.
Nucleation / Ed. by Zettlemoyer A.C. New York: M. Dekker, 1969.
Cacciuto A., Auer S., Frenkel D. // Nature. 2004. V. 428. P. 404.
Toxvaerd S. // Mol. Simul. 2004. V. 30. P. 179.
Schmitz F., Virnau P., Binder K. // Phys. Rev. E. 2013. V. 87. P. 053302.
Шевкунов С.В. // ТВТ. 2013. Т. 51. С. 86.
Коденев Г.Г., Самодуров А.В., Балдин М.Н., Бакланов А.М. // Коллоид. журн. 2014. Т. 76. С. 42.
Кучма А.Е, Щекин А.К., Марков М.Н. // Коллоид. журн. 2014. Т. 76. С. 752.
Курасов В.Б. // Коллоид. журн. 2015. Т. 77. С. 501.
Курасов В.Б. // Коллоид. журн. 2014. Т. 77. С. 745.
Аджемян Л.Ц., Щекин А.К., Бабинцев И.А. // Коллоид. журн. 2017. Т. 79. С. 237.
Корценштейн Н.М., Петров Л.В. // Коллоид. журн. 2017. Т. 79. С. 276.
Winkler P.V., Steine G., Vrtala A., Vehkamäki H., Noppe M., Lehtinen K.E.J., Reischl G.P., Wagner P.E., Kulmala M. // Science. 2008. V. 319. P. 1374.
Рыбин Е.Н. // Коллоид. журн. 2009. Т. 71. С. 101.
Бринь A.A., Фисенко С.П. // Коллоид. журн. 2007. Т. 69. С. 725.
Шевкунов С.В. // ТВТ. 2012. Т. 50. С. 274.
Шишкова И.Н., Ястребов А.К. // Коллоид. журн. 2015. Т. 77. С. 669.
Evans J.W., Thiel P.A., Bartelt M.C. // Surf. Sci. Rep. 2006. V. 61. P. 1.
Han Y., Li M., Evans J.W. // J. Chem. Phys. 2016. V. 145. P. 211911.
Шевкунов С.В. // Коллоид. журн. 2018. Т. 80. С. 224.
Шевкунов С.В. // Коллоид. журн. 2018. Т. 80. С. 241.
Zhang X.X., Lü Y.J., Chen M. // Mol. Phys. 2013. V. 111. P. 3808.
Zielke S.A., Bertram A.K., Patey G.N. // J. Phys. Chem. B. 2015. V. 119. P. 9049.
Zielke S.A., Bertram A.K., Patey G.N. // J. Phys. Chem. B. 2016. V. 120. P. 2291.
Brovchenko I., Geiger A., Oleinikova A., Paschek D. // Eur. Phys. J. E. 2003. V. 12. P. 69.
Meloni S., Giacomello A., Casciola C.M. // J. Chem. Phys. 2016. V. 145. P. 211802.
Шевкунов С.В. // Коллоид. журн. 2017. Т. 79. С. 644.
Миронов Е.П., Марченко И.В., Артемов В.В., Букреева Т.В. // Коллоид. журн. 2017. Т. 79. С. 304.
Shevkunov S.V. // Comp. Theor. Chem. 2016. V. 1084. P. 1.
Копаничук И.В., Ванин А.А., Бродская Е.Н. // Коллоид. журн. 2015. Т. 77. С. 634.
Баханова Р.А., Киселев В.И., Куку Е.И., Ким Н.С., Шкодкин А.В. // Труды Украинского регионального научно-исследовательского гидрометеорологического института. Вып. 242. М.: Гидрометеоиздат, 1991. С. 102.
Водопьянов М.Я., Пермяков Г.Н., Чурбанов Е.В. // Труды Всесоюзной конференции “Активные воздействия на гидрометеорологические процессы”. СПб: Гидрометеоиздат, 1995. Т. 2. С. 166.
Bruintjes R. // Bull. Am. Meteorol. Soc. 1999. V. 80. P. 805.
Батиста Л., Беляев В.П., Вальдес М., Данелян Б.Г., Зацепина Л.П., Зимин Б.И., Колосков Б.П., Мартинес Д., Перес К., Серегин Ю.А. // Труды Центральной аэрологической обсерватории. 1992. Вып. 177. С. 44.
Ким Н.С. // Труды Центральной аэрологической обсерватории. 1980. Вып. 142. С. 89.
Киттель Ч. Статистическая термодинамика. М.: Наука, 1977.
Wang C., Lu H., Wang Z., Xiu P., Zhou B., Zuo G., Wan R., Hu J., Fang H. // Phys. Rev. Lett. 2009. V. 103. P. 137 801.
Cassie A.B.D., Baxter S. // Trans. Faraday Soc. 1944. V. 40. P. 546.
Wenzel R.N. // Ind. Eng. Chem. 1936. V. 28. P. 988.
Singha S.K., Das P.K., Maiti B. // J. Chem. Phys. 2015. V. 142. P. 104706.
Trobo M.L., Albano E.V., Binder K. // J. Chem. Phys. 2018. V. 148. P. 114701.
Young Y. // Philos. Trans. R. Soc. London. 1805. V. 95. P. 65.
Wei J., Zhang X., Song F., Shao Y. // J. Chem. Phys. 2018. V. 148. P. 064704.
Замалин В.М., Норман Г.Э., Филинов В.С. Метод Монте-Карло в статистической термодинамике. М.: Наука, 1977.
Шевкунов С.В. // Коллоид. журн. 2005. Т. 67. С. 561.
Шевкунов С.В. // Коллоид. журн. 2009. Т. 71. С. 404.
Шевкунов С.В. // Коллоид. журн. 2015. Т. 77. С. 384.
Шевкунов С.В. // Коллоид. журн. 2016. Т. 78. С. 124.
Bitetti-Putzer R., Yang W., Karplus M. // Chem. Phys. Lett. 2003. V. 377. P. 633.
Галимзянов Б.Н., Мокшин А.В. // Коллоид. журн. 2017. Т. 79. С. 16.
Lyubartsev A.P., Martsinovski A.A., Shevkunov S.V., Vorontsov-Velyaminov P.N. // J. Chem. Phys. 1992. V. 96. P. 1776.
Burov S.V., Vorontsov-Velyaminov P.N., Piotrovskaya E.M. // Mol. Simul. 2006. V. 32. P. 437.
Atamas A., Koudriachova M.V., de Leeuw S.W., Sweatman M.B. // Mol. Simul. 2011. V. 37. P. 284.
Okamoto Y. // Mol. Simul. 2012. V. 38. P. 1282.
Lincoff J., Sasmal S., Head-Gordon T. // J. Chem. Phys. 2016. V. 145. P. 174107.
Шевкунов С.И. // Коллоид. журн. 2019. Т. 81. С. 86.
Шевкунов С.В. // ЖЭТФ. 2008. Т. 134. С. 1130.
Шевкунов С.В. // Коллоид. журн. 2006. Т. 68. С. 391.
Шевкунов С.В. // Коллоид. журн. 2006. Т. 68. С. 691.
Шевкунов С.В. // Коллоид. журн. 2014. Т. 76. С. 243.
Шевкунов С.В. // Докл. АН. 2011. Т. 438. С. 752.
Шевкунов С.В. // Коллоид. журн. 2012. Т. 74. С. 612.
Шевкунов С.В. // Коллоид. журн. 2012. Т. 74. С. 634.
Шевкунов С.В. // Коллоид. журн. 2005. Т. 67. С. 548.
Шевкунов С.В. // Коллоид. журн. 2013. Т. 75. С. 494.
Шевкунов С.В. // Коллоид. журн. 2017. Т. 79. С. 347.
Шевкунов С.В. // Коллоид. журн. 2011. Т. 73. С. 267.
Шевкунов С.В. // Коллоид. журн. 2011. Т. 73. С. 123.
Шевкунов С.В. // Коллоид. журн. 2014. Т. 76. С. 533.
Шевкунов С.В. // Коллоид. журн. 2016. Т. 78. С. 509.
Дополнительные материалы отсутствуют.
Инструменты
Коллоидный журнал


