Коллоидный журнал, 2019, T. 81, № 1, стр. 24-30

Дисперсия поляризуемости и поверхностная электропроводность частиц гетита в водном электролите KCl

В. В. Войтылов^1, *, А. В. Войтылов¹, А. В. Волкова¹, С. А. Клемешев¹, М. П. Петров¹, А. А. Трусов¹

¹ Санкт-Петербургский государственный университет, физический факультет
198504 Санкт-Петербург, Петродворец, Ульяновская ул., 1, Россия

^* E-mail: vojtylov@gmail.com

Поступила в редакцию 17.04.2018

DOI: 10.1134/S0023291219010154

Полный текст (PDF)

Аннотация

Представлены результаты изучения электрических поляризуемости и поверхностной проводимости частиц гетита в водных полидисперсных системах. Для экспериментального исследования поляризуемости частиц использован электрооптический метод. Найдены функции распределения частиц по значениям их анизотропии поляризуемости и размерам. Для суспензий, содержащих добавки электролита KCl, экспериментально определены зависимости анизотропии поляризуемости частиц от частоты электрического поля в области частот от 500 Гц до 2.5 МГц. Определены также зависимости анизотропии поляризуемости и поверхностной проводимости частиц от концентрации KCl в суспензиях. Согласно этим зависимостям поляризуемость частиц уменьшается, а поверхностная проводимость увеличивается с ростом концентрации KCl. Поверхностная проводимость частиц изменяется пропорционально концентрации KCl.

ВВЕДЕНИЕ

Поляризуемость – это важная характеристика коллоидных частиц, величина которой обусловлена поверхностной проводимостью, представленной диффузной обкладкой двойного электрического слоя (ДЭС) [1–3]. Экспериментальное изучение поляризуемости частиц в сочетании с ее теоретическим описанием позволяет определить поверхностную проводимость частиц и влияние на нее ионного состава дисперсионной среды. Первая теория поляризуемости частиц сферической [2, 3] и сфероидальной [4, 5] формы, связанная с поляризацией диффузной части ДЭС, хорошо себя оправдала при электрооптическом и кондуктометрическом исследовании дисперсных систем в области частот 5−50 кГц [6, 7]. Эта теория была переработана, границы ее применимости расширены [8], однако степень применимости теории к реальным дисперсным системам требует экспериментальной проверки. Важной особенностью данной теории является возможность ее использования в широкой области частот приложенного к частицам электрического поля, что позволяет исследовать как низкочастотную α-дисперсию, так и высокочастотную (максвелл-вагнеровскую) дисперсию поляризуемости частиц.

Для исследований были выбраны водные суспензии частиц гетита, имеющих иглообразную форму. Этот выбор был также обусловлен практической применимостью частиц гетита в качестве адсорбента тяжелых металлов [8–12], а также пигмента [13].

В работе проведены электрооптические исследования дисперсии поляризуемости частиц в области радиочастот с целью определения применимости теории, учитывающей поляризуемость коллоидной частицы на высоких и низких частотах, к описанию электрооптических эффектов в реальных полидисперсных суспензиях гетита. С целью изучения влияния добавок электролитов на поляризуемость и поверхностную проводимость частиц исследовались суспензии с разными концентрациями KCl.

ПРИГОТОВЛЕНИЕ И СВОЙСТВА СУСПЕНЗИЙ ГЕТИТА

Для получения водных суспензий был использован желтый порошок гетита с иглообразными частицами длиной менее 2 мкм и толщиной менее 0.15 мкм. Перед получением исследованных водных суспензий проводилась дополнительная очистка дисперсной фазы, включающая многократное отстаивание, ультразвуковую обработку и центрифугирование. Центрифугирование также использовалось для понижения доли частиц с размерами менее 100 нм и более 2 мкм. Полученная таким методом дисперсная фаза состава α-FeOOH добавлялась к дистиллированной воде, встряхивалась и подвергалась ультразвуковой обработке. Для определения концентрации частиц в полученных суспензиях и оценки расстояния между частицами определяли значения плотности полученной суспензии $\rho $ и дисперсионной среды ${{\rho }_{0}}$ при заданной температуре. Плотность частиц гетита ${{\rho }_{{\text{C}}}}$ была равна 4.3 г/см³. Объемную долю дисперсной фазы в суспензиях ${{\Delta V} \mathord{\left/ {\vphantom {{\Delta V} {V,}}} \right. \kern-0em} {V,}}$ необходимую для определения концентрации частиц, рассчитывали по формуле

(1)

$\frac{{\Delta V}}{V} = \frac{{\rho - {{\rho }_{0}}}}{{{{\rho }_{{\text{C}}}} - {{\rho }_{0}}}}.$

В проводимых электрооптическими методами исследованиях она не превышала 10⁻⁵, что позволяет полагать, что среднее расстояние между частицами существенно превышало их размеры. Суспензии периодически встряхивали и подвергали ультразвуковой обработке с целью предотвращения образования агрегатов. Электронно-микроскопические наблюдения, выполненные в процессе подготовки проб, показали, что частицы при высыхании капель суспензий на кварцевой подложке образуют неупорядоченные агрегаты. В исследованных дисперсных системах гетита после их встряхивания и ультразвуковой обработки такие агрегаты не наблюдаются. На рис. 1 представлен снимок частиц гетита, полученный в сканирующем электронном микроскопе. Видно, что частицы сильно вытянуты, и их форму можно аппроксимировать как цилиндрами, так и эллипсоидами вращения.

Рис. 1.

Электронно-микроскопическое изображение частиц гетита.

ЭЛЕМЕНТЫ ТЕОРИИ И ОСНОВНЫЕ ФОРМУЛЫ

Поляризуемость частиц

Ранее [8] была построена теория поляризуемости в широкой области частот, применимая к диэлектрическим частицам сфероидальной формы в электролитах. Рассмотрены два механизма, связанные с влиянием ионов на поляризацию частиц и имеющие времена релаксации в радиочастотной области.

Первый механизм связан с низкочастотной дисперсией поляризуемости (α-дисперсией) ДЭС [3, 14]. Это – механизм концентрационной поляризации ДЭС. Время релаксации ${{\tau }_{\alpha }}$ такой поляризации близко к времени перемещения ионов за счет диффузии на расстояние, равное размеру частицы l, и определяется соотношением

(2)

${{\tau }_{\alpha }} \approx \frac{{{{l}^{2}}}}{{2{{D}_{{\text{e}}}}}},$

где константа

${{D}_{{\text{e}}}} = \frac{{{{D}^{ + }}{{D}^{ - }}({{z}^{ + }} + {{z}^{ - }})}}{{{{z}^{ + }}{{D}^{ + }} + {{z}^{ - }}{{D}^{ - }}}}$

определяется константами диффузии анионов ${{D}^{ - }}$ и катионов ${{D}^{ + }},$ а также их валентностями ${{z}^{ - }}$ и ${{z}^{ + }}$ соответственно [2].

Второй механизм связан с максвелл-вагнеровской дисперсией поляризации, которая обусловлена формированием под действием внешнего поля заряда свободными ионами электролита у поверхности частиц. Этот заряд локализован в области диффузной части их ДЭС, а время его формирования ${{\tau }_{{{\text{MW}}}}}$ определяется соотношением

(3)

${{\tau }_{{{\text{MW}}}}} = \frac{1}{{{{D}_{{\text{e}}}}{{\kappa }^{2}}}}.$

Здесь $\kappa $ − обратный дебаевский радиус экранирования ДЭС.

Теория поляризуемости коллоидной частицы, пригодная для исследования реальных полидисперсных систем в электрических полях радиодиапазона, должна учитывать оба механизма поляризации частиц. Такая теория, как уже сказано выше, была построена в [8]. Она учитывает образование диполя частицы в поле за счет поляризации как вещества частицы, так и ее ДЭС. Ниже представлены основные соотношения этой теории для поляризуемости диэлектрической сфероидальной частицы в электролите. Эти соотношения были использованы в данной работе.

Поляризуемости сфероидальной частицы вдоль и перпендикулярно оси симметрии можно характеризовать двумя компонентами, ${{\gamma }_{{||}}}$ и ${{\gamma }_{ \bot }}$ соответственно. Они учитывают задержку по фазе между полем и поляризацией частиц в рамках теорий Максвелла–Вагнера и α-дисперсии и могут быть представлены в комплексном виде. Анизотропия поляризуемости $\gamma $, обуславливающая момент сил, вращающих несферическую частицу в электрическом поле, определяется действительными частями ${{\gamma }_{{||}}}$ и ${{\gamma }_{ \bot }}$. Ее можно представить соотношением

(4)

$\gamma = \operatorname{Re} ({{\gamma }_{{||}}}) - \operatorname{Re} ({{\gamma }_{ \bot }}).$

Обобщенные формулы, учитывающие влияние круговой частоты поля $\omega = 2\pi \nu $ на поляризуемость частицы, имеют вид [8]

(5)

$\begin{gathered} {{\gamma }_{{||, \bot }}} = \gamma _{{||, \bot }}^{{(\infty )}} + (\gamma _{{||, \bot }}^{{(i)}} - \gamma _{{||, \bot }}^{{(\infty )}})F(\omega ,{{\tau }_{{{\text{MW}}||, \bot }}}) + \\ + \,\,(\gamma _{{||, \bot }}^{{(0)}} - \gamma _{{||, \bot }}^{{(i)}})F(\omega ,{{\tau }_{{\alpha ||, \bot }}}), \\ \end{gathered} $

где

(6)

$\gamma _{{||, \bot }}^{{(0,i,\infty )}} = \frac{{a{{b}^{2}}}}{3}\frac{{\chi _{{||, \bot }}^{{(0,i,\infty )}} - 1}}{{1 + (\chi _{{||, \bot }}^{{(0,i,\infty )}} - 1){{A}_{{||, \bot }}}}},$

a, b – длины полуосей сфероида, и a направлена вдоль оси его вращения. Для вытянутых сфероидов ($a > b$) факторы деполяризации равны:

(7)

$\begin{gathered} {{A}_{{||}}} = \frac{{a{{b}^{2}}}}{{{{h}^{3}}}}\left[ {{\text{arctg}}\frac{h}{a} - \frac{h}{a}} \right],\,\,\,\,{{A}_{ \bot }} = {{(1 - {{A}_{{||}}})} \mathord{\left/ {\vphantom {{(1 - {{A}_{{||}}})} 2}} \right. \kern-0em} 2}, \\ h = \sqrt {{{a}^{2}} - {{b}^{2}}} . \\ \end{gathered} $

Безразмерные параметры $\chi _{{||\,,\, \bot }}^{{(0,\,i,\,\infty )}}$ определяются, соответственно, диэлектрическими проницаемостями частиц и дисперсионной среды ${{\varepsilon }_{{\text{P}}}}$ и ${{\varepsilon }_{{\text{m}}}},$ значениями их электропроводности ${{K}_{{\text{P}}}}$ и ${{K}_{{\text{m}}}}$ и поверхностной проводимости ${{K}^{\sigma }}.$ Эти параметры можно представить отношениями

(8)

$\chi _{{||, \bot }}^{{(\infty )}} = \frac{{{{\varepsilon }_{{\text{P}}}}}}{{{{\varepsilon }_{{\text{m}}}}}},\,\,\,\,\chi _{{||, \bot }}^{{(0)}} = \frac{{{{K}_{{\text{P}}}}}}{{{{K}_{{\text{m}}}}}}\,\,{\text{и }}\,\,\chi _{{||, \bot }}^{{(i)}} = \frac{{{{K}_{{\text{P}}}} + {{P}_{{||, \bot }}}{{K}^{\sigma }}}}{{{{K}_{{\text{m}}}}}}.$

При подстановке значений $\chi _{{||, \bot }}^{{(0,i,\infty )}}$ из формулы (8) в формулу (6) можно получить соответствующие значения для $\gamma _{{||, \bot }}^{{(\infty )}},$ $\gamma _{{||, \bot }}^{{(0)}}$ и $\gamma _{{||, \bot }}^{{(i)}}.$ Коэффициенты ${{P}_{{||}}}$ и ${{P}_{ \bot }}$ зависят только от длин полуосей эллипсоидов, которыми аппроксимируются частицы:

(9)

$\begin{gathered} {{P}_{{||}}} = \frac{{3a}}{{2bh}}\left[ {\frac{{{{a}^{2}} - 2{{b}^{2}}}}{{{{h}^{2}}}}{\text{arctg}}\frac{h}{b} + \frac{b}{h}} \right], \\ {{P}_{ \bot }} = \frac{{3a}}{{2bh}}\left[ {\frac{{{{a}^{2}}}}{{2{{h}^{2}}}}{\text{arcctg}}\frac{b}{h} + \frac{{b({{a}^{2}} - 2{{b}^{2}})}}{{2{{a}^{2}}h}}} \right]. \\ \end{gathered} $

Множители $F(\omega ,\tau )$ во втором и третьем слагаемых (5) в случае синусоидального поля определяются соотношением

(10)

$F(\omega ,\tau ) = \frac{1}{{1 + i\omega \tau }},$

в котором характерное время релаксации $\tau $ в разных областях дисперсии разное. В области максвелл-вагнеровской дисперсии оно определяется соотношением

(11)

${{\tau }_{{{\text{MW}}||, \bot }}} = {{\varepsilon }_{0}}\frac{{{{\varepsilon }_{{\text{m}}}} + ({{\varepsilon }_{{\text{P}}}} - {{\varepsilon }_{{\text{m}}}}){{A}_{{||, \bot }}}}}{{{{K}_{{\text{m}}}} + ({{K}_{{\text{P}}}} - {{K}_{{\text{m}}}}){{A}_{{||, \bot }}}}},$

а в области α-дисперсии соотношением

(12)

${{\tau }_{{\alpha ||, \bot }}} = {{\tau }_{{{\text{MW||,}} \bot }}}{{(l\kappa )}^{2}}.$

Размер частицы $l,$ определяющий величину ${{\tau }_{{\alpha ||}}},$ принадлежит интервалу $l \in [2a,2b]$, и при хаотической ориентации эллипсоидов можно использовать соотношение

$l \approx 2\sqrt {\frac{1}{3}{{a}^{2}} + \frac{2}{3}{{b}^{2}}} .$

Формулы для строгого определения времени релаксации ${{\tau }_{{\alpha \;||, \bot }}}$ поляризуемости в области α-дисперсии приведены в работе [8].

В случае поля несинусоидальной формы следует использовать разложение его в ряд Фурье. Влияние частот этих гармоник на анизотропию поляризуемости частиц, согласно соотношениям (4) и (5), определяется множителям $F(\omega ,\tau ),$ который может быть рассчитан при использовании формул (11) и (12) для каждой из гармоник. Для описания $F(\omega ,\tau )$ при использовании меандра с частотой $\omega $ формулу (10) следует заменить формулой

(13)

$F(\omega ,\tau ) = 1 - \frac{{4i\omega \tau }}{{{{\pi }^{2}}}}\left( {{{H}_{{ - \frac{{i + \omega \tau }}{{2\omega \tau }}}}} + \ln (4)} \right).$

Здесь i – мнимая единица, H_n – гармоническое число [15] (H_n определяется для целых чисел, а в формуле (13) индекс непрерывный).

При сопоставлении экспериментально определенных и рассчитанных с помощью формул (5)–(13) дисперсионных зависимостей ${{\gamma }_{{||}}},$ ${{\gamma }_{ \bot }}$ и $\gamma $ следует учитывать, что (5) строго выполняется для одновалентного электролита, когда константы диффузии катионов ${{D}^{ + }}$ и анионов ${{D}^{ - }}$ равны. К таким электролитам относится раствор KCl в воде, для которого ${{D}^{ + }}$ ≈ ${{D}^{ - }}$. В случае электролитов, для которых ${{D}^{ + }}$ и ${{D}^{ - }}$ существенно различны, соотношение (5) справедливо только приближенно.

Электрооптический эффект

В электрическом поле константа мутности суспензии гетита становится зависящей от поляризации проходящего сквозь нее света. В проведенных электрооптических экспериментах узкий пучок неполяризованного белого света проходил сквозь ячейку Керра, заполненную исследуемой суспензией. Прошедший луч разбивался на два луча, которые были линейно поляризованы вдоль и перпендикулярно вектору напряженности поля в ячейке и имели интенсивности ${{J}_{{||}}}$ и ${{J}_{ \bot }},$ соответственно. При хаотической ориентации частиц в ячейке ${{J}_{{||}}} = {{J}_{ \bot }},$ а при их упорядоченной ориентации под действием поля ${{J}_{{||}}} \ne {{J}_{ \bot }},$ так как у суспензии появляется консервативный дихроизм. После измерения интенсивностей ${{J}_{{||}}}$ и ${{J}_{ \bot }}$ величина дихроизма определялась соотношением

(14)

$N = \ln ({{{{J}_{ \bot }}} \mathord{\left/ {\vphantom {{{{J}_{ \bot }}} {{{J}_{{||}}}}}} \right. \kern-0em} {{{J}_{{||}}}}}).$

При возрастании напряженности поля $E$ в ячейке ориентация частиц меняется от хаотической до полной вдоль поля, а величина $N$ – от 0 до ${{N}_{{\max }}}$. При стационарной ориентации частиц в электрическом поле достаточно высокой частоты (${\omega \mathord{\left/ {\vphantom {\omega {2\pi }}} \right. \kern-0em} {2\pi }} > 1$ кГц) справедливо соотношение [6, 7]

(15)

$N({{E}^{2}}) = \int\limits_{\gamma 1}^{\gamma 2} {{{\Phi }_{{{\text{st}}}}}(\gamma ,{{E}^{2}})\Delta K{{\varphi }_{{\text{p}}}}(\gamma ){\text{d}}\gamma } ,$

в котором

(16)

$\begin{gathered} {{\Phi }_{{{\text{st}}}}}(\gamma ,{{E}^{2}}) = \\ = {{\frac{3}{2}\int\limits_0^1 {{{x}^{2}}\exp \left( {\frac{{\gamma {{E}^{2}}{{x}^{2}}}}{{2{{k}_{{\text{B}}}}T}}} \right){\text{d}}x} } \mathord{\left/ {\vphantom {{\frac{3}{2}\int\limits_0^1 {{{x}^{2}}\exp \left( {\frac{{\gamma {{E}^{2}}{{x}^{2}}}}{{2{{k}_{{\text{B}}}}T}}} \right){\text{d}}x} } {\int\limits_0^1 {\exp \left( {\frac{{\gamma {{E}^{2}}{{x}^{2}}}}{{2{{k}_{{\text{B}}}}T}}} \right){\text{d}}x} }}} \right. \kern-0em} {\int\limits_0^1 {\exp \left( {\frac{{\gamma {{E}^{2}}{{x}^{2}}}}{{2{{k}_{{\text{B}}}}T}}} \right){\text{d}}x} }} - \frac{1}{2}, \\ \end{gathered} $

${{\varphi }_{{\text{p}}}}(\gamma )$ − функция распределения частиц по $\gamma $, $\Delta K$ − дихроический вес частиц, который меняется пропорционально их длинам $L$, если они имеют форму сильно вытянутых эллипсоидов. В случае релаксации дихроизма справедливо соотношение

(17)

$N(t) = \int\limits_{L1}^{L2} {\exp ( - 6Dt)\Delta K{{\varphi }_{{\text{r}}}}(L){\text{d}}L} ,$

в котором ${{\varphi }_{{\text{r}}}}(L)$ − функция распределения частиц по их длинам, $D\,$ − константа вращательной диффузии частицы [16], которая для сильно вытянутой частицы равна

(18)

$D = \frac{{3kT}}{{\pi \eta {{L}^{3}}}}\left( {\ln 2p - 0.5} \right).$

Здесь $\eta $ − константа вязкости дисперсионной среды. Если экспериментально определить зависимости $N({{E}^{2}})$ и $N(t),$ то функции распределения частиц с дихроическим весом, а именно ${{f}_{{\text{p}}}}(\gamma ) = $ = $\Delta K{{\varphi }_{{\text{p}}}}(\gamma )$ и ${{f}_{{\text{r}}}}(L) = $ $\Delta K{{\varphi }_{{\text{r}}}}(L),$ могут быть рассчитаны [17] как решения уравнений (15) и (17). Нормировка этих функций распределения равна:

(19)

${{N}_{{\max }}} = \int\limits_{\gamma 1}^{\gamma 2} {{{f}_{{\text{p}}}}(\gamma ){\text{d}}\gamma } = \int\limits_{L1}^{L2} {{{f}_{{\text{r}}}}(L){\text{d}}L} .$

Среднее значение анизотропии поляризуемости частиц, определенное как

(20)

$\left\langle \gamma \right\rangle = \int\limits_{\gamma 1}^{\gamma 2} {\gamma {\kern 1pt} {{f}_{{\text{p}}}}} (\gamma ){\text{d}}\gamma {\text{,}}$

может быть также рассчитано по формуле [17]

(21)

$\left\langle \gamma \right\rangle = \frac{{15{{k}_{{\text{B}}}}T}}{{{{N}_{{\max }}}}}{{\left( {\frac{{{\text{d}}N}}{{{\text{d}}{{E}^{2}}}}} \right)}_{{E = 0}}}$

после определения зависимости $N({{E}^{2}})$ в области слабых полей и значения ${{N}_{{\max }}}$ в области сильных полей.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

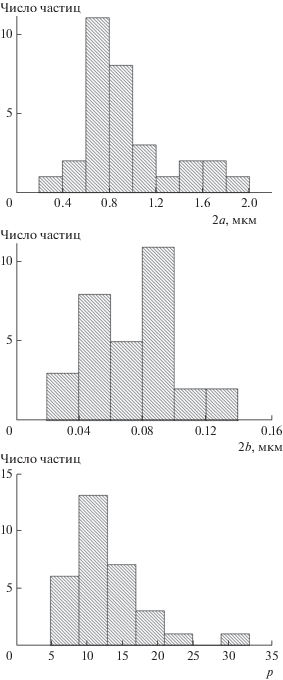
Были определены размеры частиц в предположении, что они имеют форму сфероидов с длинной полуосью $a$ и короткой $b$. Корреляции между длинами полуосей и их отношением $p = {a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b}$ не наблюдалось. Длина частицы $L$ полагалась равной $2a$. Гистограммы распределения частиц по размерам представлены на рис. 2.

Рис. 2.

Гистограмы распределения частиц гетита по длинам полуосей $a$, $b$ и значениям отношения $p = {a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b}$ при их аппроксимации эллипсоидами вращения.

Длины частиц гетита и световых волн близки, что приводит к существенному рассеянию света суспензиями гетита и позволяет наблюдать электрооптические эффекты при низких значениях объемной доли дисперсной фазы, а именно, при

$1 \times {{10}^{{ - 5}}} < \frac{{\Delta V}}{V} < 1 \times {{10}^{{ - 4}}}.$

При концентрациях частиц, отвечающих таким их объемным долям, величина дихроизма $N$ пропорциональна концентрации частиц. Это свидетельствовало о том, что расстояние между частицами велико, рассеяние ими света − однократное, а варьирование концентрации частиц не приводит к дополнительному образованию агрегатов. Значения электропроводности полученных дисперсных систем гетита в отсутствие электролита были близки к электропроводности дистиллированной воды и не превышали 4 мкСм/см.

Экспериментальная зависимость $N({{E}^{2}})$ в поле частотой 10 кГц и определенная по ней как решение уравнения (15) функция ${{f}_{{\text{p}}}}(\gamma )$ представлены на рис. 3.

Рис. 3.

Зависимости $N({{E}^{2}})$ (точки) и ${{f}_{p}}(\gamma )$ (сплошная кривая), определенные при поляризации частиц гетита на частоте 10 кГц.

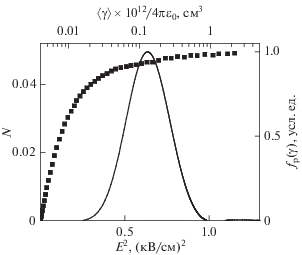
Значение $\left\langle \gamma \right\rangle = $ $2.7 \times \,\,{{10}^{{ - 13}}}$ см³ было рассчитано по формуле (20) при использовании функции ${{f}_{{\text{p}}}}(\gamma ),$ изображенной на рис. 3, а значение $\left\langle \gamma \right\rangle = $ = $2.6 \times \,\,{{10}^{{ - 13}}}$ см³ было рассчитано из наклона зависимости $N({{E}^{2}})$ по формуле (21). Эти значения близки, что подтверждает применимость формул (20) и (21) для определения $\left\langle \gamma \right\rangle $ и надежность рассмотренной электрооптической методики исследования поляризуемости частиц.

Зависимость $N(t)$, определенная экспериментально, и соответствующая ей функция ${{f}_{{\text{r}}}}(L)\,$, рассчитанная как решение уравнения (17), представлены на рис. 4.

Рис. 4.

Релаксационная зависимость $N(t)$ (спадающая сплошная кривая) и функция распределения $f(L)$ (пунктир).

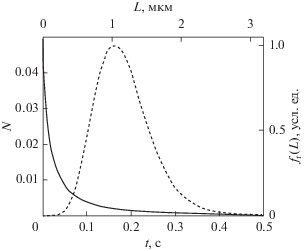
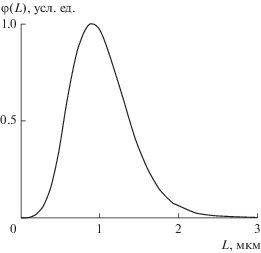
Функция распределения $f(L)\,$ содержит дихроический вес, который пропорционален $L$. Истинная функция распределения частиц по длинам может быть рассчитана по формуле

(22)

$\varphi (L) = {{f(L){{L}^{{ - 1}}}} \mathord{\left/ {\vphantom {{f(L){{L}^{{ - 1}}}} {\int\limits_{L1}^{L2} f (L){{L}^{{ - 1}}}{\text{d}}L}}} \right. \kern-0em} {\int\limits_{L1}^{L2} f (L){{L}^{{ - 1}}}{\text{d}}L}}.$

Она представлена на рис. 5.

Рис. 5.

Зависимость $\varphi (L)$ для водного коллоида гет-ита.

Изображенная на рис. 5 зависимость $\varphi (L)$ согласуется с гистограммой, представленной на рис. 2 ($L = 2a\,$). Это показывает, что в суспензиях гетита агрегирование незначительно и слабо влияет на наблюдаемый электрооптический эффект.

Были экспериментально определены зависимости анизотропии поляризуемости частиц гетита от частоты поля $\nu $, приложенного к суспензиям, как не содержащим электролита, так и содержащим добавки KCl. Величина поляризуемости частиц гетита (как α-FeOOH, так и β-FeOOH) существенно зависит от pH среды [18]. Изменение концентрации KCl практически не влияет на значение pH суспензий, которое было равно 7.2. Зависимости $\left\langle \gamma \right\rangle $ от $\nu $ также были рассчитаны теоретически. При расчетах были использованы формулы (4)–(12) теории поляризуемости частиц, гистограммы, представленные на рис. 2 и позволяющие учесть полидисперсность суспензий, электропроводность суспензий ${{K}_{{\text{m}}}},$ измеренная экспериментально, и поверхностная проводимость частиц ${{K}^{\sigma }},$ варьируемая как свободный параметр. За правильное значение ${{K}^{\sigma }}$ принималось то, которое обеспечивало наилучшее соответствие (в рамках метода наименьших квадратов) теоретической и экспериментальной зависимостей $\left\langle \gamma \right\rangle $ от $\nu $. Для четырех суспензий (C₀–C₃), три из которых содержат добавки KCl, значения ${{K}_{{\text{m}}}}$ и ${{K}^{\sigma }}$ приведены в табл. 1.

Таблица 1.

Зависимость поверхностной проводимости частиц от концентрации электролита

Суспензия	${{C}_{{{\text{KCl}}}}}$, ${{{\text{м м о л ь }}} \mathord{\left/ {\vphantom {{{\text{м м о л ь }}} {\text{л }}}} \right. \kern-0em} {\text{л }}}$	${{K}^{\sigma }} \times {{10}^{{11}}}$, ${\text{O}}{{{\text{м }}}^{{ - {\text{1}}}}}$	${{K}_{{\text{m}}}}$, ${{{\text{м к С м }}} \mathord{\left/ {\vphantom {{{\text{м к С м }}} {{\text{с м }}}}} \right. \kern-0em} {{\text{с м }}}}$
C₀	0	1.3	3.7
C₁	0.024	7.7	20
C₂	0.036	11	30
C₃	0.06	18	50

На рис. 6 представлены дисперсионные зависимости $\left\langle \gamma \right\rangle $ в области частот ν прямоугольных импульсов от 500 Гц до 2.5 МГц, определенные экспериментально и рассчитанные при значениях ${{K}_{{\text{m}}}}$ и ${{K}^{\sigma }}$, приведенных в табл. 1.

Рис. 6.

Зависимости $\left\langle \gamma \right\rangle $ от частоты поля $\nu $. Точки – экспериментальные данные, сплошные кривые – результаты теоретического расчета. Концентрация KCl (ммоль/л): 1 – 0, 2 – 0.025, 3 – 0.035, 4 – 0.06.

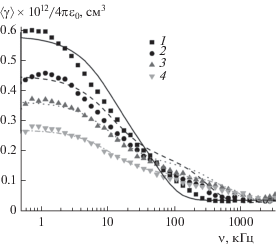
Области частот 1−500 кГц соответствует спад $\left\langle \gamma \right\rangle .$ Аналогичный спад поляризуемости ранее наблюдался при исследовании суспензий как β-FeOOH [19], так и иного состава [20, 21].

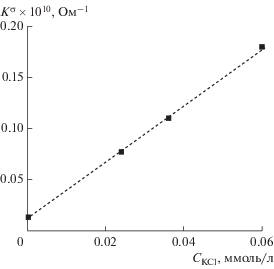
Как можно видеть на рис. 6, экспериментально определенные и теоретически рассчитанные дисперсионные зависимости согласуются. Это свидетельствует о применимости теории поляризуемости коллоидных частиц к суспензиям иглообразных частиц гетита. В случае синусоидальных полей теоретические и экспериментальные зависимости $\left\langle \gamma \right\rangle $ от $\nu $ также близки. Исследования зависимости $\left\langle \gamma \right\rangle $ от ${{C}_{{{\text{KCl}}}}}$ позволяют заключить, что при частотах менее 100 кГц поляризуемость частиц гетита уменьшается с увеличением концентрации KCl в дисперсионной среде. Поверхностная проводимость частиц, напротив, возрастает при увеличении концентрации KCl. Зависимость поверхностной проводимости частиц гетита от концентрации KCl в суспензиях представлена на рис. 7. Видно, что в области низких концентраций KCl поверхностная проводимость частиц гетита ${{K}^{\sigma }}$ линейно зависит от концентрации электролита, что согласуется с законом Генри. Аналогичные зависимости $\left\langle \gamma \right\rangle $ и ${{K}^{\sigma }}$ от концентрации KCl наблюдаются и в случае водных коллоидов алмаза [22].

Рис. 7.

Зависимость поверхностной проводимости частиц гетита ${{K}^{\sigma }}$ от концентрации электролита KCl в суспензии.

ВЫВОДЫ

1. Исследования электрического дихроизма в водных суспензиях гетита позволяют получить надежные данные о степени полидисперсности суспензий и распределении частиц по значениям их анизотропии поляризуемости.

2. Сопоставление экспериментально исследованных и теоретически рассчитанных дисперсионных зависимостей поляризуемости частиц показало, что теоретическая модель, учитывающая их концентрационную поляризуемость и максвелл-вагнеровскую дисперсию, вполне применима при описании поляризуемости частиц гетита в электролитах. Это позволяет определять поверхностную электрическую проводимость частиц и влияние на нее электролитов.

3. Добавление одновалентного электролита KCl к водной суспензии гетита понижает поляризуемость частиц и повышает их поверхностную проводимость. Зависимость поверхностной проводимости от концентрации KCl носит линейный характер в области малых концентраций.

Работа выполнена при поддержке Российского фонда фундаментальных исследований, грант 16-03-00495a.

Часть исследований проведена в Междисциплинарном ресурсном центре по направлению “Нанотехнологии” Научного парка Санкт-Петербургского государственного университета.

Список литературы

O’Konski C.T. // J. Phys. Chem. 1960. V. 64. P. 605.
Духин С.С. Электропроводность и электрокинетические свойства дисперсных систем. Киев: Наукова думка, 1975.
Духин С.С., Шилов В.Н. Диэлектрические явления и двойной электрический слой в дисперсных системах и полиэлектролитах. Киев: Наукова думка, 1972.
Еремова Ю.Я., Шилов В.Н. // Коллоид. журн. 1975. Т. 37. С. 635.
Еремова Ю.Я., Шилов В.Н. // Коллоид. журн. 1975. Т. 37. С. 1090.
Войтылов В.В., Толстой Н.А., Трусов А.А. // Коллоид. журн. 1980. Т. 42. С. 1051.
Trusov A., Vojtylov V. Electrooptics and Conductometry of Polydisperse Systems. New York: CRC Press, 1993.
Shilov V.N., Borkovskaja Yu.B., Budankova S.N. // Molecular and Colloidal Electro-Optics. Surfactant Science Series. V. 134 / Ed. by Stoylov S.P., Stoimeno-va M.V. Boca Raton: CRC Press, 2007. P. 39.
Антонова А.С., Кропачева Т.Н., Дидик М.В., Корнев В.И. // Вестник Казанского технологического университета. 2014. Т. 17. № 4. С. 48.
Антонова A.С., Кропачева Т.Н., Новикова Н.В., Корнев B.И. // Вестник технологического университета. 2016. Т. 19. № 2. С. 17.
Cornell R.M., Schwertman U. The Iron Oxides: Structure, Properties, Reactions, Occurrences and Uses. Weinheim: Wiley-VCH, 2003.
Семушин В.В., Печенюк С.И. // Сорбционные и хроматографические процессы. 2008. Т. 8. С. 106 .
Ермилов П.И., Индейкин Е.А., Толмачев И.А. Пигменты и пигментированные лакокрасочные материалы. Учебное пособие для вузов. Л.: Химия, 1987.
Шилов В.Н., Духин С.С. // Коллоид. журн. 1970. Т. 32. С. 393.
Conway J.H., Guy R.K. The Book of Numbers. New York: Springer-Verlag, 1996.
Цветков В.Н., Эскин В.Е., Френкель С.Я. Структура макромолекул в растворах. М.: Наука, 1964.
Spartakov A.A., Trusov A.A., Voitylov A.V., Vojtylov V.V. // Molecular and Colloidal Electro-Optics. Surfactant Science Series. V. 134 / Ed. by Stoylov S.P., Stoimeno-va M.V. Boca Raton: CRC Press, 2007. P. 193.
Miteva S., Stoimenova M. // J. Colloid Interface Sci. 2004. V. 273. P. 490.
Milkova V., Radeva Ts., Stoimenova M. // J. Colloid Interface Sci. 2008. V. 319. P. 435.
Zhivkov A.M., Hristov R.P. // RSC Adv. 2014. V. 4. P. 2715.
Zhivkov A.M., Gyurova A.Y. // J. Phys. Chem. B. 2009. V. 113. P. 8375.
Petrov M.P., Shilov V.N., Trusov A.A., Voitylov A.V., Vojtylov V.V. // Colloids Surf. A. 2016. V. 456. P. 114.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Коллоидный журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал