Коллоидный журнал, 2020, T. 82, № 2, стр. 195-203

Обтекание жидкой сферы, заполненной неньютоновской жидкостью и внедренной в пористую среду

Ramasamy Selvi¹, Pankaj Shukla¹, А. Н. Филиппов^2, *

¹ Vellore Institute of Technology
600127 Chennai, India

² РГУ нефти и газа (НИУ) им. И.М. Губкина
119991 Москва, Ленинский просп., 65, корп. 1, Россия

^* E-mail: filippov.a@gubkin.ru

Поступила в редакцию 30.07.2019
После доработки 23.08.2019
Принята к публикации 26.08.2019

DOI: 10.31857/S0023291220010127

Полный текст (PDF)

Аннотация

Исследуется обтекание неньютоновской жидкой частицы Рейнера–Ривлина, окруженной ньютоновской жидкостной оболочкой и внедренной в проницаемую среду. Такая постановка задачи характерна, например, при изучении движения капли нефти, окруженной водной средой (прямая эмульсия), в пористом коллекторе под действием внешнего перепада давления. Аналогичная задача возникает при просачивании лимфы в ткани организма человека и животных. Течение внутри проницаемого слоя описывается уравнением Бринкмана, поток в области, лежащей между жидкостью Рейнера–Ривлина и пористой средой, – уравнением Стокса, а течение во внутренней сферической области – уравнением Рейнера–Ривлина. Общее решение для функции тока во внешней пористой области записывается в терминах модифицированной функции Бесселя и полиномов Гегенбауэра, а для жидкой сферы Рейнера–Ривлина решение определяется путем разложения функции тока в степенной ряд по малому безразмерному параметру S. Решение краевой задачи находится путем сопряжения граничных условий для всех областей. Определена сила сопротивления, действующая на жидкую частицу Рейнера–Ривлина, встроенную в проницаемую среду. Изучено влияние на коэффициент сопротивления значений параметра проницаемости α, отношения вязкостей λ и безразмерного параметра S. Соответствующие зависимости представлены графически и обсуждены. Предельными переходами выведены известные частные случаи.

ВВЕДЕНИЕ

В физико-химической механике сплошной среды тензорно нелинейные определяющие соотношения, связывающие девиаторы напряжений и скоростей деформаций в несжимаемых изотропных средах, называют жидкостями Рейнера–Ривлина [1, 2]. Среда Рейнера–Ривлина моделирует поведение неньютоновской жидкости со сложной внутренней микроструктурой. Как правило, модель Рейнера–Ривлина подходит для описания течения коллоидных растворов, а также “мягких” материалов, таких как суспензии, грязи, нефти, жидкие полимеры, кровь в капиллярной системе и других биологическиx материалoв.

Изучение потока жидкости через проницаемые среды является наиболее важным и актуальным исследованием при интенсификации очистки воды, разработке нефтяных технологий и водоносных горизонтов, где сложная жидкость и пористая среда являются двумя фазами, участвующими в процессе переноса. В середине прошлого века благодаря введению поперечной вязкости, характерной для модели среды Рейнера–Ривлина, удалось объяснить [1, 3] явление “центростремительного насоса”, обнаруженное Вайссенбергом в экспериментах по изучению течений очень вязких жидкостей, такиx как растворы каучука, целлюлозы, крахмала, пористый битум. Такие течения направлены противоположно центробежной силе и силе тяжести.

Проницаемая среда обычно обладает системой пор, стенки которых покрыты жидкостью. В последние годы различные модели пористых сред находят применение при анализе биомеханических и геофизических процессов, в инженерных приложениях в нефтяной и нефтедобывающей промышленности, при решении задач смазки и течения жидкости на неподвижных слоях и т.п. Многие авторы применяют закон Дарси [4], когда жидкость течет через тело, охватываемое насыщенной проницаемой средой. Закон Дарси хорошо работает при течении вязких жидкостей или газов через пористые слои перпендикулярно их плоскопараллельным границам или в случае медленных течений через неограниченные, в общем случае анизотропные среды, когда вводится тензор проницаемостей. Если же пористая среда граничит с непроницаемой стенкой или чистой жидкостью, то применение уравнений Дарси вызывает затруднения ввиду некорректности постановки краевых задач, связанной соответственно с невозможностью удовлетворить условие прилипания и с разным порядком уравнений Дарси и Стокса. В этом случае удобнее и предпочтительнее использовать уравнения Бринкмана [5].

Бринкман разработал свою модель, используя закон Дарси и уравнение Стокса. Позднее уравнение Бринкмана было теоретически подтверждено Тамом [6] и Лундгреном [7]. Задача описания ползущего течения около непроницаемого кругового цилиндра, охватываемого проницаемой средой, не подчиняющейся закону Дарси, была поставлена и решена Попом и Ченгом [8]. Они также определили замкнутую форму точного решения для функции тока. Цинь и Калони [9] исследовали задачу нахождения тензора напряжений, определяемого проницаемой средой Бринкмана, и получили гидродинамическую силу, действующую на пористую сферу в однородном потоке. Перепелкин, Старов и Филиппов [10] изучали течение вязкой ньютоновской жидкости через пористую частицу, расположенную в центре жидкой сферической ячейки. Было получено аналитическое решение краевой задачи для уравнения Бринкмана, описывающей течение через полностью пористую частицу внутри концентрической жидкой оболочки. Представлены решения для случая полного перемешивания и неперемешивания жидкостей внутри и снаружи частицы. Выведены формулы для силы, действующей на частицу. Позднее Васин, Старов и Филиппов [11] решили задачу о движении сферической частицы, состоящей из непроницаемого ядра, покрытого недеформируемым и гидродинамически однородным пористым слоем, с постоянной скоростью в неограниченной несжимаемой вязкой жидкости. Ими получена конечная алгебраическая формула для определения силы, действующей на частицу в общем случае различной вязкости жидкости внутри и снаружи пористого слоя. Аналогичная задача обтекания непроницаемой сферы, покрытой пористой оболочкой, была исследована Барманом [12] тоже с использованием модели Бринкмана. Он нашел решение для функции тока, дающей постоянную скорость жидкости, вытекающей из сферы. Впоследствии Рудрайя [13] исследовал задачу течения жидкости вокруг несжимаемой сферы, покрытой высоковязкой проницаемой средой Бринкмана, и нашел точное решение уравнения движения, дающее течение через сферу с постоянной на бесконечности скоростью. Сринивасачарья и Мерти [14] получили решение задачи обтекания жидкостью осесимметричного тела, помещенного в проницаемую среду, и получили новую формулу для силы со стороны жидкости, покоящейся на бесконечности. Васин, Старов и Филиппов [15] опубликовали обзор, посвященный применению ячеечного метода для исследования гидродинамической проницаемости пористых/дисперсных сред и мембран. На основе ячеечного метода была рассчитана гидродинамическая проницаемость пористого слоя/мембраны, образованного твердыми частицами с пористой оболочкой и непористым непроницаемым ядром. Рассмотрены и сравнены результаты для четырех известных граничных условий на внешней границе ячейки: Хаппеля, Кувабары, Квашнина и Каннингема (обычно называемое условием Мехты–Морзе). Позже Део и Шукла [16] вычислили силу, действующую на жидкую сферу, покрытую пористой средой. Део и Гупта [17] рассчитали сопротивление пористой сферы, находящейся в другой проницаемой среде, и исследовали влияние удельной проницаемости каждой из этих сред, моделируемых по Бринкману, на силу сопротивления частицы.

Задача обтекания жидкой сферы Рейнера–Ривлина, внедренной в насыщенную пористую среду Бринкмана, изучалась Джейсвалем и Гуптой [18] – мы в данной работе следуем их обозначениям при рассмотрении обтекания жидкой сферы Рейнера–Ривлина, окруженной оболочкой, заполненной ньютоновской жидкостью и внедренной в пористую среду. Такая постановка задачи характерна, например, при изучении движения капли нефти, окруженной водной средой (прямая эмульсия), в пористом коллекторе под действием внешнего перепада давления. Аналогичная задача возникает при просачивании лимфы в ткани организма человека и животных. Отметим, что недавно Джейсвал [19] обобщил задачу, рассмотренную в [18], на случай движения сферы Рейнера–Ривлина в среде Бринкмана, насыщенной микрополярной жидкостью. Из других работ следует упомянуть статью Саада [20], который исследовал ячеечные модели течения микрополярной жидкости вокруг вязкой жидкой сферы. Особенности применения ячеечной модели для течений микрополярной жидкости и корректная постановка ряда краевых задач для сферы и цилиндра рассмотрены в обзоре [21]. Отметим также, что сравнение результатов моделей Дарси и Бринкмана при медленном течении вязкой жидкости через пористый слой с непроницаемыми стенками дано в работе [22].

ПОСТАНОВКА ЗАДАЧИ

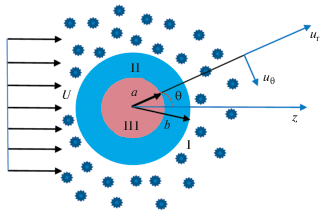
Рассмотрим сферу радиуса a с жидкостью Рейнера–Ривлина (область III), помещенную в концентрическую сферическую оболочку внешнего радиуса b, содержащую ньютоновскую жидкость (область II). Система сфера–оболочка помещена в неограниченную пористую среду (область I), через которую медленно течет (“ползет”) несжимаемая жидкость вязкости μ₁ с постоянной на бесконечности скоростью U, направленной вдоль положительного направления оси z (рис. 1).

Рис. 1.

Физическая картина обтекания слоистой сферы.

Таким образом, насыщенная пористая среда с параметром проницаемости α (определен ниже) является жесткой, изотропной, однородной и содержит сферическую каплю жидкости Рейнера–Ривлина (область III) вязкости μ₃. Введем сферическую полярную систему координат (r, θ, φ) с началом в центре сферы и выберем луч φ = 0 в качестве оси z в направлении свободного потока насыщающей жидкости (рис. 1). Верхние индексы в скобках у переменных или параметров i = 1, 2, 3 обозначают номер области.

Для внешней области I, занятой проницаемой средой, будем использовать уравнение Бринкмана [23]

(1)

${{\tilde {\nabla }}^{2}}{{\tilde {u}}^{{\left( 1 \right)}}} - {{\left( {\frac{\alpha }{b}} \right)}^{2}}{{\tilde {u}}^{{\left( 1 \right)}}} = \frac{1}{{{{\mu }_{{\text{e}}}}}}\tilde {\nabla }{{\tilde {p}}^{{\left( 1 \right)}}},\,\,\,\,b \leqslant r < \infty ~$

вместе с условием несжимаемости

(2)

$\tilde {\nabla }\,\cdot\,{{\tilde {u}}^{{\left( 1 \right)}}} = 0,\,\,\,\,b \leqslant r < \infty .$

Здесь $\alpha = \sqrt {\frac{{{{\mu }_{1}}~{{b}^{2}}}}{{{{\mu }_{{\text{e}}}}\kappa }}} ~$ – безразмерный параметр проницаемости, $\kappa $ – удельная проницаемость пористой среды Бринкмана а ${{\mu }_{{\text{e}}}}$ – ее эффективная вязкость, ${{\mu }_{1}}$ – вязкость чистой жидкости в областях I и II, ${{\tilde {u}}^{{\left( i \right)}}}$ и ${{\tilde {p}}^{{\left( i \right)}}}$ – векторы скорости и давление в i-ой области соответственно.

В области II предполагаем существование ползущего течения, подчиняющегося уравнению Стокса [24]

(3)

${{\mu }_{1}}{{\tilde {\nabla }}^{{2~}}}{{\tilde {u}}^{{\left( 2 \right)}}} = \tilde {\nabla }{{\tilde {p}}^{{\left( 2 \right)}}},\,\,\,\,a \leqslant r < b$

и условию несжимаемости

(4)

$\tilde {\nabla }\,\cdot\,~{{\tilde {u}}^{{\left( 2 \right)}}} = 0,\,\,\,\,a \leqslant r < b.$

Для области III примем уравнения состояния изотропной неньютоновской жидкости в следующей форме:

(5)

${{\tilde {\tau }}_{{ij}}} = - {{\tilde {p}}^{{\left( 3 \right)}}}{{\tilde {\delta }}_{{ij}}} + 2{{\mu }_{3}}{{\tilde {d}}_{{ij}}} + {{\mu }_{{\text{c}}}}{{\tilde {d}}_{{ik}}}{{\tilde {d}}_{{kj}}},$

где ${{\tilde {d}}_{{ij}}} = \frac{1}{2}\left( {\tilde {u}_{{i,j}}^{{\left( 3 \right)}} + \tilde {u}_{{j,i}}^{{\left( 3 \right)}}} \right)$ – тензор скоростей деформаций, ${{\mu }_{3}}$ – коэффициент кажущейся вязкости жидкости в капле, ${{\tilde {\tau }}_{{ij}}}$ – тензор напряжений, а ${{\mu }_{{\text{c}}}}$ – поперечная вязкость (cross viscosity) жидкости Рейнера–Ривлина. Тогда можем записать уравнения движения и неразрывности этой жидкости соответственно в виде

(6)

$\tilde {\tau }_{{ij,j}}^{{\left( 3 \right)}} = \rho \tilde {u}_{k}^{{\left( 3 \right)}}\tilde {u}_{{i,k}}^{{\left( 3 \right)}},$

(7)

$\tilde {\nabla }\,\cdot\,{{\tilde {u}}^{{\left( 3 \right)}}} = 0,\,\,\,\,0 \leqslant r < a.$

Здесь и выше запятая означает дифференцирование по стоящей за ней координате, точка означает скалярное произведение, а ρ – плотность жидкости, которая предполагается одинаковой во всех областях.

Поскольку течение является осесимметричным, то функция тока во всех областях не зависит от азимутального угла φ: $\psi = \psi \left( {r,\theta } \right).$ Компоненты скорости в сферической системе координат в этом случае выражаются через производные функции тока по оставшимся переменным:

${{\tilde {u}}_{r}} = - \frac{1}{{{{r}^{2}}{\text{sin}}\theta }}\frac{{\partial \psi }}{{\partial \theta }}~,\,\,\,\,{{\tilde {u}}_{\theta }} = \frac{1}{{r{\text{sin}}\theta }}\frac{{\partial \psi }}{{\partial r}}~.$

Для удобства решения вводим следующие безразмерные переменные и величины – они обозначены теми же буквами, но без знака тильда:

$\tilde {r} = br,\,\,\,\,~{{\tilde {u}}_{\theta }} = U{{u}_{\theta }},\,\,\,\,~{{\tilde {u}}_{r}} = U{{u}_{r}},\,\,\,\,{{\tilde {d}}_{{ij}}} = \frac{U}{b}{{d}_{{ij}}},$

${{\tilde {\tau }}_{{ij}}} = {{\mu }_{1}}\frac{U}{b}{{\tau }_{{ij}}},\,\,\,\,~\tilde {\psi } = U{{b}^{2}}\psi ,\,\,\,\,\tilde {p} = {{\mu }_{1}}\frac{U}{b}p,$

где U – упомянутая выше постоянная скорость обтекания. Граничные условия будут сформулированы ниже.

МЕТОД РЕШЕНИЯ

В предположении малости безразмерного параметра $S = \frac{{{{\mu }_{{\text{c}}}}U}}{{{{\mu }_{3}}b}}$ решение для функции тока и давления внутри жидкого ядра (капли Рейнера–Ривлина) будем искать в виде степенного разложения по этому параметру,

(8)

$\begin{gathered} {{\psi }^{{\left( 3 \right)}}} = {{\psi }_{0}} + {{\psi }_{1}}S + {{\psi }_{2}}~{{S}^{2}} + \ldots , \\ {{p}^{{\left( 3 \right)}}} = {{p}_{0}} + {{p}_{1}}~S + {{p}_{2}}~{{S}^{2}} + \ldots . \\ \end{gathered} $

Рамкиссун показал [25], что функции тока ${{\psi }_{0}},$ ${{\psi }_{1}}$ и ${{\psi }_{2}}$ удовлетворяют следующим дифференциальным уравнениям:

(9)

$\begin{gathered} {{E}^{4}}{{\psi }_{0}} = 0,\,\,\,\,{{E}^{4}}{{\psi }_{1}} = 8r{\text{si}}{{{\text{n}}}^{2}}\theta {\text{cos}}\theta , \\ {{E}^{4}}{{\psi }_{2}} = \frac{{32}}{3}{{r}^{2}}{\text{si}}{{{\text{n}}}^{2}}\theta {\text{.}} \\ \end{gathered} $

Частные решения уравнений (9) могут быть представлены в виде

(10)

$\begin{gathered} {{\psi }_{0}} = \left( {{{r}^{4}} - {{r}^{2}}} \right){\text{si}}{{{\text{n}}}^{2}}\theta ,\,\,\,\,{{\psi }_{1}} = \frac{2}{{21}}{{r}^{5}}{\text{si}}{{{\text{n}}}^{2}}\theta {\text{cos}}\theta , \\ {{\psi }_{2}} = \frac{2}{{63}}{{r}^{6}}{\text{si}}{{{\text{n}}}^{6}}\theta {\text{.}} \\ \end{gathered} $

После исключения давления из уравнений (1) и (3) получим в безразмерном виде два уравнения для функций тока в областях I и II соответственно:

(11)

$~{{E}^{2}}\left( {{{E}^{2}} - {{\alpha }^{2}}} \right){{\psi }^{{\left( 1 \right)}}} = 0,$

(12)

${{E}^{4}}{{\psi }^{{\left( 2 \right)}}} = 0,$

где оператор Стокса $~{{E}^{2}}$ представляется как

(13)

$~{{E}^{2}} = \frac{\partial }{{\partial {{r}^{2}}}} + \frac{{{\text{sin}}\theta }}{{{{r}^{2}}}}\frac{\partial }{{\partial \theta }}\left( {\frac{1}{{{\text{sin}}\theta }}\frac{\partial }{{\partial \theta }}} \right).$

Выражения для безразмерных касательных (тангенциальных) и нормальных (радиальных) напряжений через функцию тока в областях I и II в сферической полярной системе координат можно найти в монографии Хаппеля и Бреннера [24]:

(14)

$\tau _{{r\zeta }}^{{\left( {\text{i}} \right)}} = \frac{{{{{{\mu }_{{\text{i}}}}} \mathord{\left/ {\vphantom {{{{\mu }_{{\text{i}}}}} {{{\mu }_{1}}}}} \right. \kern-0em} {{{\mu }_{1}}}}}}{{r\sqrt {1 - {{\zeta }^{2}}} }}\left[ {\frac{{{{\partial }^{2}}{{\psi }^{{\left( {\text{i}} \right)}}}}}{{\partial {{r}^{2}}}} - \frac{2}{r}\frac{{\partial {{\psi }^{{\left( {\text{i}} \right)}}}}}{{\partial r}} - \frac{{1 - {{\zeta }^{2}}}}{{{{r}^{2}}}}\frac{{{{\partial }^{2}}{{\psi }^{{\left( {\text{i}} \right)}}}}}{{\partial {{\zeta }^{2}}}}} \right],$

(15)

$\tau _{{rr}}^{{\left( {\text{i}} \right)}} = - {{p}^{{\left( {\text{i}} \right)}}} - 2\frac{{{{{{\mu }_{{\text{i}}}}} \mathord{\left/ {\vphantom {{{{\mu }_{{\text{i}}}}} {{{\mu }_{1}}}}} \right. \kern-0em} {{{\mu }_{1}}}}}}{{{{r}^{2}}}}\left[ {\frac{2}{r}\frac{{\partial {{\psi }^{{\left( {\text{i}} \right)}}}}}{{\partial \zeta }} - \frac{{{{\partial }^{2}}{{\psi }^{{\left( {\text{i}} \right)}}}}}{{\partial r\partial \zeta }}} \right],$

где $\zeta = r{\text{cos}}\theta ,$ $i = 1,~\,\,2.$ Безразмерное давление в обеих областях I и II находится интегрированием следующих выражений:

(16)

$\begin{gathered} \frac{{\partial {{p}^{{\left( 1 \right)}}}}}{{\partial r}} = - \frac{{{{{{\mu }_{{\text{e}}}}} \mathord{\left/ {\vphantom {{{{\mu }_{{\text{e}}}}} {{{\mu }_{1}}}}} \right. \kern-0em} {{{\mu }_{1}}}}}}{{{{r}^{2}}{\text{sin}}\theta }}\frac{\partial }{{\partial \theta }}\left[ {\left( {{{E}^{2}} - {{\alpha }^{2}}} \right){{\psi }^{{\left( 1 \right)}}}} \right], \\ ~\frac{{\partial {{p}^{{\left( 1 \right)}}}}}{{\partial \theta }} = \frac{{{{{{\mu }_{{\text{e}}}}} \mathord{\left/ {\vphantom {{{{\mu }_{{\text{e}}}}} {{{\mu }_{1}}}}} \right. \kern-0em} {{{\mu }_{1}}}}}}{{r{\text{sin}}\theta }}\frac{\partial }{{\partial r}}\left[ {\left( {{{E}^{2}} - {{\alpha }^{2}}} \right){{\psi }^{{\left( 1 \right)}}}} \right], \\ \end{gathered} $

(17)

$\begin{gathered} \frac{{\partial {{p}^{{\left( 2 \right)}}}}}{{\partial r}} = - \frac{1}{{{{r}^{2}}{\text{sin}}\theta }}\frac{\partial }{{\partial \theta }}\left[ {{{E}^{2}}{{\psi }^{{\left( 2 \right)}}}} \right], \\ \frac{{\partial {{p}^{{\left( 2 \right)}}}}}{{\partial \theta }} = \frac{1}{{r{\text{sin}}\theta }}\frac{\partial }{{\partial r}}\left[ {{{E}^{2}}{{\psi }^{{\left( 2 \right)}}}} \right]. \\ \end{gathered} $

В случае осесимметричного установившегося течения вязкой несжимаемой жидкости общее решение уравнения Бринкмана (11) получил Златановский [23], а частное решение уравнения Стокса (12) – Хаппель и Бреннер [24]. В случае наличия оси симметрии z в сферических полярных координатах эти решения могут быть записаны как

(18)

$\begin{gathered} {{\psi }^{{\left( 1 \right)}}}\left( {r,\zeta } \right) = \left[ {{{r}^{2}} + {{B}_{1}}{{r}^{{ - 1}}} + {{C}_{1}}\sqrt r {{K}_{{\frac{3}{2}}}}\left( {\alpha r} \right)} \right]{{G}_{2}}\left( \zeta \right), \\ 1 \leqslant r \leqslant \infty , \\ \end{gathered} $

(19)

$\begin{gathered} {{\psi }^{{\left( 2 \right)}}}\left( {r,\zeta } \right) = \left[ {{{A}_{2}}{{r}^{{ - 1}}} + {{B}_{2}}r + {{C}_{2}}{{r}^{2}} + {{D}_{2}}{{r}^{4}}} \right]{{G}_{2}}\left( \zeta \right), \\ \gamma \leqslant r \leqslant 1, \\ \end{gathered} $

где обозначено $\gamma = {a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b},$ ${{G}_{n}}\left( \zeta \right)$ – функция Гегенбауэра [26], ${{K}_{{\frac{3}{2}}}}$ – функция Макдональда полуцелого индекса, а B₁, C₁, A₂, B₂, C₂, D₂, a₂ и b₂ – неизвестные постоянные, которые должны быть определены из граничных условий.

Для течения внутри сферы с жидкостью Рейнера–Ривлина, Рамкиссун показал [25], что функция тока дается выражением

(20)

$\begin{gathered} {{\psi }^{{\left( 3 \right)}}}\left( {r,\zeta } \right) = {{\psi }_{0}} + {{\psi }_{1}}S + {{\psi }_{2}}{{S}^{2}} + \\ + \,\,\mathop \sum \limits_{n = 2}^\infty \left[ {{{A}_{n}}{{r}^{n}} + {{B}_{n}}{{r}^{{n + 2}}}} \right]{{G}_{n}}\left( \zeta \right). \\ \end{gathered} $

После подстановки выражений для ${{\psi }_{0}},$ ${{\psi }_{1}},$ ${{\psi }_{2}}$ в уравнение (20), приходим к явному выражению

(21)

$\begin{gathered} {{\psi }^{{\left( 3 \right)}}}\left( {r,\zeta } \right) = \left[ {\left( {{{a}_{2}} - 2} \right){{r}^{2}} + \left( {{{b}_{2}} + 2} \right){{r}^{4}} + \frac{4}{{63}}{{S}^{2}}{{r}^{6}}} \right] \times \\ \times \,\,{{G}_{2}}\left( \zeta \right) + \left[ {{{a}_{3}}{{r}^{3}} + \left( {{{b}_{3}} + \frac{4}{{21}}S} \right){{r}^{5}}} \right]{{G}_{3}}\left( \zeta \right) + \\ + \,\,\mathop \sum \limits_{n = 4}^\infty \left[ {{{A}_{n}}{{r}^{n}} + {{B}_{n}}{{r}^{{n + 2}}}} \right]{{G}_{n}}\left( \zeta \right),\,\,\,\,0 \leqslant r \leqslant \gamma . \\ \end{gathered} $

ГРАНИЧНЫЕ УСЛОВИЯ

Неизвестные постоянные, фигурирующие в решениях для функции тока (18), (19) и (21), определяются из нижеследующих граничных условий.

Граница сферической ячейки $r = 1$

Предположение о непроницаемости межфазной границы жидкой двухслойной капли с пористой средой приводит к двум уравнениям,

(22)

${{\psi }^{{\left( 1 \right)}}} = 0,\,\,\,\,{{\psi }^{{\left( 2 \right)}}} = 0.$

Полагаем, что тангенциальная скорость непрерывна при переходе через эту границу, т.е.,

(23)

$\frac{{\partial {{\psi }^{{\left( 1 \right)}}}}}{{\partial r}} = \frac{{\partial {{\psi }^{{\left( 2 \right)}}}}}{{\partial r}}.$

Считаем также, что касательные напряжения непрерывны на рассматриваемой поверхности, так что

(24)

$\tau _{{r\theta }}^{{\left( 1 \right)}} = \tau _{{r\theta }}^{{\left( 2 \right)}}.$

Отметим, что совокупность граничных условий (22)–(24) задает отсутствие перемешивания жидкостей на границе ячейки. Аналогичные условия поставим и на границе между жидкой сферой Рейнера–Ривлина и ньютоновской жидкостью.

Граница жидкой сферы Рейнера–Ривлина $r = \gamma $

Условия отсутствия перемешивания неньютоновской и ньютоновской жидкостей дают три уравнения, аналогичные уравнениям (22)–(24):

(25)

${{\psi }^{{\left( 2 \right)}}} = 0\,\,\,\,{\text{и}}\,\,\,\,{{\psi }^{{\left( 3 \right)}}} = 0,$

(26)

$\frac{{\partial {{\psi }^{{\left( 2 \right)}}}}}{{\partial r}} = \frac{{\partial {{\psi }^{{\left( 3 \right)}}}}}{{\partial r}},$

(27)

$~{{\mu }_{1}}\frac{\partial }{{\partial r}}\left( {\frac{1}{{{{r}^{2}}}}\frac{{\partial {{\psi }^{{\left( 2 \right)}}}}}{{\partial r}}} \right) = {\text{\;}}{{\mu }_{3}}\frac{\partial }{{\partial r}}\left( {\frac{1}{{{{r}^{2}}}}\frac{{\partial {{\psi }^{{\left( 3 \right)}}}}}{{\partial r}}} \right).$

Выражение для безразмерной касательной компоненты тензора напряжений (5) жидкости Рейнера–Ривлина в сферической полярной системе координат $\left( {r,\theta ,\varphi } \right)$ принимает вид: ${{\tau }_{{r\theta }}} = {{2{{\mu }_{3}}} \mathord{\left/ {\vphantom {{2{{\mu }_{3}}} {{{\mu }_{1}}{{d}_{{r\theta }}}}}} \right. \kern-0em} {{{\mu }_{1}}{{d}_{{r\theta }}}}} - S{{d}_{{r\theta }}}{{d}_{{\varphi \varphi }}}$ [18]. Предполагаем слабое влияние поперечной вязкости на касательные напряжения, поэтому ввиду малости параметра S и компонент тензора скоростей деформаций приближенно имеем ${{\tau }_{{r\theta }}} = {{2{{\mu }_{3}}} \mathord{\left/ {\vphantom {{2{{\mu }_{3}}} {{{\mu }_{1}}{{d}_{{r\theta }}}}}} \right. \kern-0em} {{{\mu }_{1}}{{d}_{{r\theta }}}}}.$ Мы учитываем здесь межфазное натяжение на границе капли со слоем ньютоновской жидкости, что приводит к разрыву нормальной компоненты ${{\tau }_{{rr}}}$ тензора напряжений и никак не влияет на касательное напряжение ${{\tau }_{{r\theta }}},$ которое непрерывно. Последнее обстоятельство позволяет записать $\tau _{{r\theta }}^{{\left( 2 \right)}} = \tau _{{r\theta }}^{{\left( 3 \right)}},$ что эквивалентно условию (27).

Подставляя общие решения уравнений Бринкмана и Стокса в разных областях в граничные условия (22)–(27), приходим к системе линейных алгебраических уравнений

(28)

${{B}_{1}} + {{C}_{1}}{{K}_{{\frac{3}{2}}}}\left( \alpha \right) = - 1,$

(29)

${{A}_{2}} + {{B}_{2}} + {{C}_{2}} + {{D}_{2}} = 0,$

(30)

$\begin{gathered} {{B}_{1}} + {{C}_{1}}\left[ {\alpha {{K}_{{\frac{1}{2}}}}\left( \alpha \right) + {{K}_{{\frac{3}{2}}}}\left( \alpha \right)} \right] - \\ - \,\,{{A}_{2}} + 2{{B}_{2}} + {{C}_{2}} + 4{{D}_{2}} = 2, \\ \end{gathered} $

(31)

$\begin{gathered} 6{{B}_{1}} + {{C}_{1}}\left[ {2\alpha {{K}_{{\frac{1}{2}}}}\left( \alpha \right) + \left( {{{\alpha }^{2}} + 6} \right){{K}_{{\frac{3}{2}}}}\left( \alpha \right)} \right] - \\ - \,\,{\text{\;}}6{{A}_{2}} - 6{{D}_{2}} = 0, \\ \end{gathered} $

(32)

${{A}_{2}} + {{\gamma }^{{ - 3}}}{{B}_{2}} + {{\gamma }^{{ - 2}}}{{C}_{2}} + {{\gamma }^{{ - 5}}}{{D}_{2}} = 0,$

(33)

${{\gamma }^{{ - 2}}}{{a}_{2}} + {{\gamma }^{{ - 4}}}{{b}_{2}} = 2{{\gamma }^{{ - 2}}} - 2{{\gamma }^{{ - 4}}} - \frac{4}{{63}}{{S}^{2}}{{\gamma }^{{ - 6}}},$

(34)

$\begin{gathered} - {{A}_{2}} + 2~{{\gamma }^{{ - 3}}}~{{B}_{2}} + \,~{{\gamma }^{{ - 2}}}~{{C}_{2}} + 4~{{\gamma }^{{ - 5}}}~{{D}_{2}} - 2~{{\gamma }^{{ - 3}}}~{{a}_{2}} - \\ - \,\,4~{{\gamma }^{{ - 5}}}~{{b}_{2}} = - 4~{{\gamma }^{{ - 3}}}~ + \,8~{{\gamma }^{{ - 5}}} + \frac{{24}}{{63}}{{S}^{2}}~{{\gamma }^{{ - 7}}},~ \\ \end{gathered} $

(35)

$\begin{gathered} 4{{\lambda }^{2}}~{{A}_{2}}~{{\gamma }^{5}}~ - ~\,2{{\gamma }^{2}}~{{\lambda }^{2}}{{B}_{2}} - 2{{\lambda }^{2}}~{{\gamma }^{3}}~{{C}_{2}} + 4{{\lambda }^{2}}{{D}_{2}} + \\ + \,\,~2{{\gamma }^{2}}~{{a}_{2}} - 4{{b}_{2}} = 4~{{\gamma }^{2}}~ + \,8 + \frac{8}{7}{{S}^{2}}~{{\gamma }^{{ - 2}}}. \\ \end{gathered} $

Система уравнений (28)–(35) была решена с использованием компьютерной оболочки Mathematica^®. В результате получены точные выражения для всех неизвестных постоянных B₁, C₁, A₂, B₂, C₂, D₂, a₂ и b₂, которые ввиду их громоздкости здесь не приводятся. Таким образом, безразмерные функции тока в областях I, II, III могут быть записаны соответственно в виде (18), (19) и

(36)

$\begin{gathered} {{\psi }^{{\left( 3 \right)}}}\left( {r,\zeta } \right) = \\ = \left[ {\left( {{{a}_{2}} - 2} \right){{r}^{2}} + \left( {{{b}_{2}} + 2} \right){{r}^{4}} + \frac{4}{{63}}{{S}^{2}}{{r}^{6}}} \right]{{G}_{2}}\left( \zeta \right), \\ 0 \leqslant r \leqslant 1. \\ \end{gathered} $

Отметим, что в (36) по сравнению с (21) отсутствуют последние два слагаемые в силу ограниченности скорости жидкости на оси z. Исходя из этого, имеем: ${{a}_{3}} = 0,$ ${{b}_{3}} = - \frac{4}{{21}}S,$ ${{a}_{n}} = 0,$ ${{b}_{n}} = 0,$ $n > 3.$

ВЫЧИСЛЕНИЕ СИЛЫ СОПРОТИВЛЕНИЯ

Сила сопротивления F, действующая на жидкую сферу, встроенную в проницаемую среду, может быть рассчитана согласно Хаппелю и Бреннеру [24] посредством интегрирования напряжений по поверхности жидкой сферы:

(37)

$F = 2\pi {{b}^{2}}\int\limits_0^\pi {\left( {\tau _{{rr}}^{{\left( 1 \right)}}~\cos \theta - \tau _{{r\theta }}^{{\left( 1 \right)}}~\sin \theta ~} \right)d\theta } ,$

где

$~\tau _{{rr}}^{{\left( 1 \right)}} = \frac{{U{{\mu }_{1}}}}{b}f\left( \alpha \right)\cos \theta ,\,\,\,\,\tau _{{r\theta }}^{{\left( 1 \right)}} = \frac{{U{{\mu }_{1}}}}{b}g\left( \alpha \right)\sin \theta ,$

$\begin{gathered} f\left( \alpha \right) = - {{\alpha }^{2}} + \frac{1}{2}\left\{ {{{\alpha }^{2}} + 12} \right\}{{B}_{1}} + \\ + \,\,{{C}_{{1~}}}\left\{ {6{{K}_{{\frac{1}{2}}}}\left( \alpha \right) + 2\alpha {{K}_{{\frac{1}{2}}}}\left( \alpha \right)} \right\}, \\ \end{gathered} $

$\begin{gathered} g\left( \alpha \right) = \frac{1}{2}\left[ {6{{B}_{1}} + {{C}_{1}}\left\{ {3{{K}_{{\frac{3}{2}}}}\left( \alpha \right) + } \right.} \right. \\ \left. {\left. { + \,\,\frac{{{{\alpha }^{2}}}}{2}{{K}_{{\frac{3}{2}}}}\left( \alpha \right) + \alpha {{K}_{{\frac{1}{2}}}}\left( \alpha \right)} \right\}} \right]. \\ \end{gathered} $

Подставляя выражения для $f\left( \alpha \right)$ и $g\left( \alpha \right)$ в уравнение (37), получаем,

(38)

$F = \frac{2}{3}~b\pi {{\alpha }^{2}}U{{\mu }_{1}}\left[ { - 2 + {{B}_{1}} - 2{{C}_{1}}{{K}_{{\frac{3}{2}}}}\left( \alpha \right)} \right],$

где произвольные постоянные ${{B}_{1}}$ и $~{{C}_{1}}$ должны быть найдены из системы (28)–(35). Коэффициент сопротивления определяется стандартным образом:

(39)

${{D}_{N}} = \frac{{2F}}{{\pi {{b}^{2}}\rho {{U}^{2}}}} = \frac{8}{3}{{\alpha }^{2}}\left[ { - 2 + {{B}_{1}} - 2{{C}_{1}}{{K}_{{\frac{3}{2}}}}\left( \alpha \right)} \right]{\text{R}}{{{\text{e}}}^{{ - 1}}},$

где введено число Рейнольдса $\operatorname{Re} = \frac{{2bU}}{\nu }$ и кинематическая вязкость $\nu = \frac{{{{\mu }_{1}}}}{\rho }.$ Безразмерное напряжение сдвига в любой точке жидкой сферы может быть найдено по формуле

(40)

$\begin{gathered} {{\tau }_{{r\theta }}} = \left[ {3{{B}_{1}} + {{C}_{{1~}}}\left\{ {\frac{1}{2}({{\alpha }^{2}} + 6){{K}_{{\frac{3}{2}}}}\left( \alpha \right) + \alpha {{K}_{{\frac{1}{2}}}}\left( \alpha \right)} \right\}} \right] \times \\ \times \,\,{\text{sin}}\theta {\text{.}} \\ \end{gathered} $

Предельные случаи

Случай 1. Если $S \to 0,$ тогда имеем сложную каплю радиуса $b,$ состоящую из двух ньютоновских несмешивающихся жидкостей в пористой среде, и сила, действующая на нее, равна

(41)

$F = {{2\pi {{\mu }_{1}}bU\left\{ { - {{\alpha }^{3}}\left( {{{a}_{0}} + {{b}_{0}} + {{с}_{0}}} \right)} \right\}} \mathord{\left/ {\vphantom {{2\pi {{\mu }_{1}}bU\left\{ { - {{\alpha }^{3}}\left( {{{a}_{0}} + {{b}_{0}} + {{с}_{0}}} \right)} \right\}} \Delta }} \right. \kern-0em} \Delta },$

где

$\begin{gathered} {{a}_{0}} = ( - 3 - 6\gamma + {{\gamma }^{2}} + 8{{\gamma }^{3}}){{\lambda }^{2}} + 3{{\alpha }^{2}}(2 - 3{{\lambda }^{2}} + \\ + \,\,\gamma (4 - 6{{\lambda }^{2}}) + 8{{\gamma }^{3}}(1 + {{\lambda }^{2}}) + {{\gamma }^{2}}(6 + {{\lambda }^{2}}), \\ \end{gathered} $

$\begin{gathered} {{b}_{0}} = 6(3 - 3{{\lambda }^{2}} - 6\gamma ( - 1 + {{\lambda }^{2}}) + \\ + \,\,{{\gamma }^{2}}(9 + {{\lambda }^{2}}) + 4{{\gamma }^{3}}(3 + 2{{\lambda }^{2}})), \\ \end{gathered} $

$\begin{gathered} {{с}_{0}} = 6\alpha (3 - 3{{\lambda }^{2}} - 6\gamma ( - 1 + {{\lambda }^{2}}) + \\ + \,\,{{\gamma }^{2}}(9 + {{\lambda }^{2}}) + 4{{\gamma }^{3}}(3 + 2{{\lambda }^{2}})), \\ \end{gathered} $

$\begin{gathered} \Delta = (6 - 3(3 + \alpha ){{\lambda }^{2}} - 6\gamma ( - 2 + (3 + \alpha ){{\lambda }^{2}}) + \\ + \,\,8{{\gamma }^{3}}(3 + \left( {3 + \alpha } \right){{\lambda }^{2}}) + {{\gamma }^{2}}(18 + \left( {3 + \alpha } \right){{\lambda }^{2}})). \\ \end{gathered} $

Этот результат является новым. Отношение ньютоновских вязкостей жидкостей обозначено здесь как ${{\lambda }^{2}} = {{{{\mu }_{1}}} \mathord{\left/ {\vphantom {{{{\mu }_{1}}} {{{\mu }_{3}}}}} \right. \kern-0em} {{{\mu }_{3}}}}.$

Случай 2. Если $S \to 0$ и $\gamma \to \infty ,$ то жидкая сфера Рейнера–Ривлина становится каплей однородной ньютоновской жидкости радиуса $a$ в пористой среде, так что имеем известный результат, полученный Део и Шукла [16]:

(42)

$\begin{gathered} F = - 2\pi {{\mu }_{1}}Ub \times \\ \times \,\,\left[ {\frac{{9 + 6{{\lambda }^{2}} + {{\alpha }^{3}}{{\lambda }^{2}} + 3{{\alpha }^{2}}(1 + {{\lambda }^{2}}) + \alpha (9 + 6{{\lambda }^{2}})}}{{3 + \left( {3 + \alpha } \right){{\lambda }^{2}}}}} \right]. \\ \end{gathered} $

Случай 3. Если $S \to 0$ и $\alpha \to 0,$ то пористая среда превращается в ньютоновскую жидкость, и получаем хорошо известный результат, представленный в монографии Хаппеля и Бреннера [24]:

(43)

$F = - 6\pi {{\mu }_{1}}Ub\left[ {\frac{{\left( {1 + \frac{2}{3}{{\lambda }^{2}}} \right)}}{{1 + {{\lambda }^{2}}}}} \right].$

Случай 4. Если ${{\lambda }^{2}} \to \infty ,$ то жидкая сфера Рейнера–Ривлина ведет себя как пузырек газа:

(44)

$F = - 2\pi {{\mu }_{1}}Ub\left[ {\frac{{6 + 6\alpha + 3{{\alpha }^{2}} + {{\alpha }^{3}}}}{{\left( {3 + \alpha } \right)}}} \right].$

Формула (44) была ранее получена Джайсвалом и Гуптой [18].

Случай 5. Если ${{\lambda }^{2}} \to 0,$ то жидкая сфера Рейнера–Ривлина становится твердой и непроницаемой, и выражение для силы

(45)

$F = - 2\pi {{\mu }_{1}}Ub~\left( {3 + 3\alpha + {{\alpha }^{2}}} \right)$

согласуется с результатом, полученным Ганапати [27].

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Перейдем теперь к оценке коэффициента сопротивления ${{D}_{{\text{N}}}}$ по формуле (39) при обтекании однородным на бесконечности потоком жидкости неньютоновской жидкой сферы, помещенной внутрь концентрической оболочки ньютоновской жидкости, окруженной проницаемой средой. Зависимость коэффициента сопротивления получена здесь для различных параметров, таких как параметр проницаемости α, отношение коэффициентов вязкости ${{\lambda }^{2}}$ и безразмерный параметр S.

На рис. 2 для случая γ = 0.09, S = 0.5 приведены зависимости, характеризующие поведение безразмерного коэффициента сопротивления D_N с ростом отношения вязкостей ${{\lambda }^{2}}$ (увеличением вязкости жидкости µ₁ в среде Бринкмана и в жидкой оболочке или уменьшением кажущейся вязкости µ₃ капли Рейнера–Ривлина). При этом задавались различные значения параметра проницаемости α, который при слабо различающихся вязкостях µ₁ и µ_e пропорционален частному ${{{{b}^{2}}} \mathord{\left/ {\vphantom {{{{b}^{2}}} \kappa }} \right. \kern-0em} \kappa }.$ Т.е. уменьшение удельной проницаемости среды Бринкмана и увеличение радиуса ньютоновской оболочки приводят к росту коэффициента сопротивления D_N, что представляется вполне физически закономерным.

Рис. 2.

Изменение коэффициента сопротивления D_N с ростом λ² для значений α = 2 (1), 4 (2), 6 (3), 10 (4) при γ = 0.09, S = 0.5.

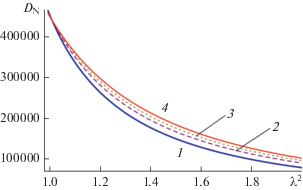
Из данных рис. 2 следует, что коэффициент сопротивления уменьшается с увеличением коэффициента ${{\lambda }^{2}},$ что соответствует результатам работ [18, 19]. Однако авторы [18, 19] не дали объяснения данному эффекту. Мы его объясняем в конце этого раздела при обсуждении касательных напряжений на поверхности капли Рейнера–Ривлина. Отметим, что рис. 2 соответствует случаю µ₁ > µ₃. Если µ₁ < µ₃, то порядок следования кривых 1–4 меняется на противоположный.

Изменение безразмерного коэффициента сопротивления D_N с ростом параметра проницаемости α для различных значений отношения коэффициентов вязкости ${{\lambda }^{2}}$ при $\gamma = 0.09$ и $S = 0.5$ изображено на рис. 3. Видно, что коэффициент сопротивления быстро увеличивается с увеличением параметра проницаемости α (уменьшением удельной проницаемости κ пористой среды). Кроме того, следует отметить, что коэффициент D_N уменьшается по мере постепенного увеличения отношения коэффициентов вязкости ${{\lambda }^{2}}$ при постоянных параметрах α, $S$ и $\gamma $ – это может быть только при одновременном уменьшении кажущейся вязкости µ₃ и поперечной вязкости µ_с или скорости потока U, что представляется вполне физически закономерным явлением.

Рис. 3.

Зависимость безразмерного коэффициента сопротивления от параметра проницаемости α для значений λ² = 1.1 (1), 1.5 (2), 1.75 (3), 1.95 (4) при ${\gamma } = 0.09$ и $S = 0.5.$

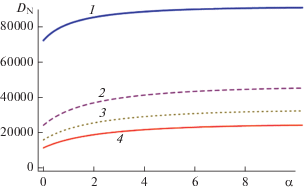
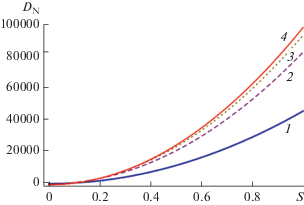
На рис. 4 показано поведение безразмерного коэффициента сопротивления D_N с ростом параметра S (увеличением поперечной вязкости неньютоновской жидкости μ_c в капле или ростом скорости потока U) при постоянных γ = 0.09, α = 0.5 и различных значениях отношения коэффициентов вязкости ${{\lambda }^{2}}.$ Видно, что коэффициент сопротивления увеличивается с ростом безразмерного параметра S, при этом сопротивление сначала быстро уменьшается с ростом параметра ${{\lambda }^{2}},$ а в области значений ${{\lambda }^{2}} \geqslant 1.5$ это уменьшение замедляется.

Рис. 4.

Зависимость безразмерного коэффициента сопротивления от S для значений λ² = 1 (1), 1.5 (2), 2 (3), 2.5 (4) при $\gamma = 0.09$ и $\alpha = 0.5.$

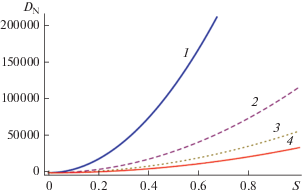
Изменение безразмерного коэффициента сопротивления D_N с ростом параметра S для значений параметра проницаемости α = 0, 3, 6, 9 при γ = 0.09 и ${{\lambda }^{2}} = 2~$ показано на рис. 5. Из представленных на нем зависимостей следует, что коэффициент сопротивления увеличивается с увеличением безразмерного параметра S (ростом поперечной вязкости жидкости Рейнера–Ривлина). При этом в области малых значений S (<0.1) D_N уменьшается с ростом α, а затем быстро увеличивается с ростом этого параметра. Это свидетельствует о сложном влиянии кажущейся и поперечной вязкостей жидкости Рейнера–Ривлина на качественное и количественное поведение силы сопротивления сложной частицы. Отметим, что случай α = 0 соответствует обтеканию капли Рейнера–Ривлина безграничным потоком ньютоновской жидкости (вырождение пористой среды).

Рис. 5.

Изменение безразмерного сопротивления D_N с ростом параметра S для значений параметра α = 0 (1), 3 (2), 6 (3), 9 (4) при γ = 0.09, ${{\lambda }^{2}} = 2.$

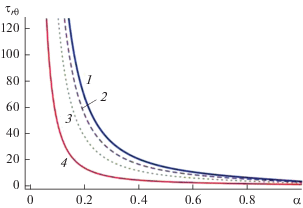
Изменение безразмерного напряжения сдвига ${{\tau }_{{r\theta }}}$ в любой точке поверхности неньютоновской жидкой сферы дается уравнением (40). Результаты расчетов максимального значения этого напряжения $\left( {\theta = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} \right)$ показаны на рис. 6 в зависимости от параметра проницаемости α для различных фиксированных значений S. Видно, что скорость падения максимального тангенциального напряжения уменьшается с ростом параметра проницаемости α, при этом тангенциальное напряжение уменьшается с увеличением безразмерного параметра S (ростом поперечной вязкости жидкости Рейнера–Ривлина). Следует отметить, что при α > 0.6 происходит существенное замедление убывания касательного напряжения. Падение касательного напряжения с ростом параметра α при прочих постоянных параметрах можно связать с уменьшением эффективной вязкости среды Бринкмана.

Рис. 6.

Изменение безразмерного максимального напряжения сдвига как функция параметра α для значений S = 0 (1), 0.5 (2), 0.75 (3), 0.99 (4) при $\gamma = 0.09,$ ${{\lambda }^{2}} = 2,$ $\theta = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}.$

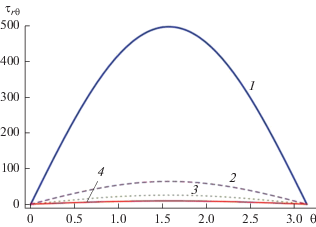
На рис. 7 показано поведение безразмерного напряжения сдвига ${{\tau }_{{r\theta }}}$ в любой точке поверхности неньютоновской жидкой сферы, находящейся в проницаемой среде, с изменением полярного угла θ для различных значений параметра проницаемости α. Очевидно, что как самые задние, так и самые передние точки на сфере, т.е. полюсы, находятся при значениях угла θ = π и θ = 0 соответственно. На полюсах сферы касательное напряжение становится равным нулю. При этом оно достигает своего наибольшего значения на экваторе, при θ = π/2 (рис. 6), что вполне закономерно. Видно также, что безразмерное напряжение сдвига уменьшается при увеличении параметра проницаемости α, т.е., в частности, при увеличении вязкости чистой жидкости µ₁ ньютоновской жидкости, и это объясняет уменьшение коэффициента сопротивления D_N с ростом µ₁, выявленное раньше (рис. 2).

Рис. 7.

Изменение безразмерного напряжения сдвига от угла θ (в радианах) на поверхности капли жидкости Ривлина–Рейнера для значений параметра α = 0.1 (1), 0.3 (2), 0.5 (3), 0.8 (4) при $\gamma = 0.09,$ ${{\lambda }^{2}} = 2$ и $S = 0.5.$

ЗАКЛЮЧЕНИЕ

В работе исследовано обтекание неньютоновской жидкой частицы Рейнера–Ривлина, окруженной ньютоновской жидкостной оболочкой и внедренной в проницаемую среду.

Течение внутри проницаемого слоя описывается уравнением Бринкмана, поток в области, лежащей между жидкостью Рейнера–Ривлина и пористой средой, – уравнением Стокса, а течение во внутренней сферической области – уравнениями Рейнера–Ривлина. Получено общее решение для функции тока во внешней пористой области в терминах модифицированной функции Бесселя и полиномов Гегенбауэра, а для жидкой сферы Рейнера–Ривлина решение определяется путем разложения функции тока в степенной ряд по малому безразмерному параметру S, зависящему от двух вязкостей капли (кажущейся и поперечной), скорости обтекания и радиуса ячейки. Определена сила сопротивления, действующая на жидкую частицу Рейнера–Ривлина, встроенную в проницаемую среду, изучена зависимость коэффициента сопротивления от различных безразмерных параметров задачи. Результаты представлены графически и обсуждены.

Предельными переходами выведены известные частные случаи, что подтверждает достоверность полученных результатов. Рассмотренная в работе модель применима к описанию движения капли прямой нефтяной эмульсии в пористом коллекторе. Полученные результаты могут быть использованы для оценки коэффициента извлечения нефти из пласта.

Список литературы

Рейнер М. Реология. М.: Мир, 1965.
Rivlin R.S., Ericksen J.L. // J. Rational Mech. Anal. 1955. V. 4. P. 323.
Малинин Н.И. // Коллоид. журн. 1960. Т. 22. С. 201.
Darcy H. Les Fontaines Publiques De La Ville De Dijion. Paris: Victor Dalmont, 1856.
Brinkman H. // Appl. Sci. Res. A1. 1947. P. 27.
Tam C. // J. Fluid Mech. 1969. V. 38. P. 537.
Lundgren T. // J. Fluid Mech. 1972. V. 51. P. 273.
Pop I., Cheng P. // Chem. Eng. Sci. 1992. V. 30. P. 257.
Qin Y., Kaloni P. // J. Eng. Math. 1988. V. 22. V. 177.
Перепелкин П.В., Старов В.М., Филиппов А.Н. // Коллоид. журн. 1992. Т. 54. С. 139.
Васин С.И., Старов В.М., Филиппов А.Н. // Кол-лоид. журн. 1996. Т. 58. С. 298.
Barman B. // Indian J. Pure Appl. Math. 1996. V. 27. P. 1244.
Rudraiah N., Shiva Kumara I. // Proceeding of Seventh Asian Cong. Fluid Mech. 1997. P. 565.
Srinivasacharya D., Murthy J. // C.R. Mecanique. 2002. V. 330. P. 417.
Vasin S.I., Filippov A.N., Starov V.M. // Adv. Colloid Interface Sci. 2008. V. 139. P. 83.
Deo S., Shukla P. // Adv. Theor. Appl. Mech. 2010. V. 3. P. 45.
Deo S., Gupta B. // J. Porous Media. 2010. V. 13. P. 1009.
Jaiswal B.R., Gupta B.R. // Transport in Porous Media. 2015. V. 106. P. 907.
Jaiswal B.R. // Appl. Math. Comp. 2018. V. 316. P. 488.
Saad E.I. // Meccanica. 2012. V. 47. P. 2055.
Ханукаева Д.Ю., Филиппов А.Н. // Коллоид. журн. 2018. Т. 80. С. 17.
Ханукаева Д.Ю., Филиппов А.Н. // Труды РГУ нефти и газа имени И.М. Губкина. 2014. № 3(276). С. 145.
Zlatanovski T. // Q. J. Mech. Appl. Math. 1999. V. 52. P. 111.
Happel J., Brenner H. Low Reynolds Number Hydrodynamics. Hague: Martinus Nijhoff Publishers, 1983.
Ramkissoon H. // J. Appl. Math. Mech. 1989. V. 69. P. 259.
Abramowitz M., Stegun I. Handbook of Mathematical Functions. New York: Dover Publications, 1970.
Ganapathy R. // Z. Angew. Math. Mech. 1997. V. 77. P. 871.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Коллоидный журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал