Коллоидный журнал, 2020, T. 82, № 4, стр. 470-475

ВВЕДЕНИЕ

В работах [1–3] рассматривалась зависимость краевого угла пузырька на твердой поверхности от давления в жидкости. Задача решается просто, если растворимость газа в жидкости пренебрежимо мала. В обратном случае нужно учитывать влияние давления на растворимость газа, а потому зависимость краевого угла от давления в газовой фазе оказывается более сложной. Если межфазная поверхность жидкость–газ плоская, то при равновесии гидростатические давления в обеих фазах всегда одинаковы. Поэтому при повышении давления в газовой фазе на некоторую величину точно на такую же величину повысится давление и в жидкой фазе. Почему же газ при этом растворяется? Из общих соображений можно сказать, что этого требует принцип Ле-Шателье, согласно которому под внешними воздействиями система перестраивается так, чтобы их эффект уменьшить. В частности, при возрастании внешнего давления любое тело должно уменьшить свой объем (в термодинамике это одно из условий устойчивости). В газе на одну молекулу приходится больший объем, чем в жидкости, а потому переход молекул из газа в жидкость способствует уменьшению объема системы.

Термодинамика дает и более детальное объяснение растворения газа в жидкости при повышении давления. Вещество всегда переходит из мест с большим химическим потенциалом в места с меньшим химическим потенциалом. Зависимость химического потенциала ${{\mu }_{i}}$ компонента i от параметров состояния дается выражением

где ${{s}_{i}}$ и ${{v}_{i}}$ – парциальные молекулярные (молярные) энтропия и объем компонента i соответственно, T – температура, p – давление, ${{x}_{k}}$ – мольная доля компонента k (индекс k пробегает значения от 1 до n – 1, где n – число компонентов). Парциальный объем молекулы вещества ${{v}_{i}}$ гораздо больше в газовой фазе, чем в жидкой. Поэтому при повышении давления в жидкости и газе на одну и ту же величину химический потенциал вещества в газе станет больше, чем в жидкости, и вещество будет переходить из газа в жидкость. Так газ растворяется в жидкости.

По мере растворения одной фазы в другой, разница между фазами уменьшается. Следовательно, поверхностное натяжение на границе жидкости и газа также должно уменьшаться (в критической точке оно обращается в нуль). Если же газ нерастворим в жидкости, то, как показывает детальный анализ этого случая [4, 5], рост давления должен приводить, наоборот, к увеличению поверхностного натяжения. Таким образом, падение или рост поверхностного натяжения с давлением газа – простой и эффективный критерий, по которому можно судить, можно ли пренебречь растворимостью данного газа. Согласно этому критерию, из простых газов наименьшей растворимостью обладает гелий, и неудивительно, что именно с гелием было проведено исследование поверхностных слоев чистых жидкостей (включая автоадсорбцию) [6–9]. В настоящее время наименее растворимым газом в воде считается тетрафторметан (коэффициент растворимости 0.0038, у гелия – 0.0083 при температуре 20°C и давлении 1 бар).

Как отмечалось в предыдущей публикации [3], детали зависимости краевого угла от параметров состояния лучше обсуждать в контексте с экспериментальными данными. Для темы этого сообщения такие данные как раз имеются. Это зависимость от давления краевого угла воды при растворении углекислого газа и краевого угла циклогексана при растворении этана в интервале давлений 1–11 бар [10]. Правда, в этой работе непосредственно измерялся наступающий (частично также отступающий) угол жидкости на стальном стержне, так что данные применимы скорее к капле, чем к пузырьку. Но фундаментальное термодинамическое уравнение для краевого угла было выведено в [3] из уравнения Юнга и уравнений адсорбции для всех трех поверхностей на линии трехфазного контакта, а потому в равной степени применимо и к капле, и к пузырьку (оба считаются малыми, но макроскопическими). Оно имеет вид

где ${{k}_{\operatorname{s} }}$ – коэффициент шероховатости твердой поверхности, γ – поверхностное натяжение жидкости, $\bar {s}$ – избыток энтропии на единицу поверхности и ${{\Gamma }_{i}}$ – адсорбция компонента i. Обозначения фаз: α – фаза с вогнутой стороны межфазной поверхности, β – наружная фаза и γ – твердая подложка. Межфазные поверхности помечены двойными индексами фаз. В данном сообщении уравнение (2) будет использовано для дальнейшего анализа. Ниже выводятся термодинамические соотношения для зависимости краевого угла капли или пузырька от давления растворяемого газа.

СЛУЧАЙ СИДЯЧЕЙ КАПЛИ

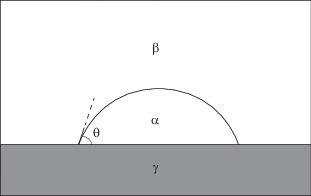
Рассмотрим сначала случай сидячей капли (рис. 1). Внутренняя фаза капли α представляет собой жидкость, а точнее – жидкий раствор смеси газов, находящихся в наружной фазе β (через которую осуществляется управление всей системой). Помимо указанной смеси газов, находящаяся под переменным давлением газовая фаза β также содержит равновесный пар жидкости, играющей роль растворителя. Будем считать, что вариация давления в фазе β происходит в изотермических условиях и, естественно, при заданной шероховатости поверхности твердого тела (фазы γ), так что уравнение (2) упрощается до формы

В формуле (3) суммирование по i относится ко всем компонентам флюидной части системы. Если обособить растворитель (дадим ему индекс j) и относить индекс i только к растворенным веществам, то (3) можно записать как

где учтено условие $\Gamma _{j}^{{\alpha \beta }} = 0$ при выборе положения разделяющей поверхности на границе жидкость–газ как эквимолекулярной поверхности в отношении растворителя. В уравнении (4) в качестве переменных фигурируют химические потенциалы, но для наших целей одной из переменных должно быть давление. Поменять ${{\mu }_{j}}$ на ${{p}^{\beta }}$ можно при помощи уравнения Гиббса–Дюгема где V – объем, S – энтропия и ${{N}_{k}}$ – число молекул компонента k. Применительно к фазе β, включающей (в виде пара) и растворитель j, в изотермических условиях уравнение (5) можно записать в виде где ${{v}^{\beta }} \equiv {{{{V}^{\beta }}} \mathord{\left/ {\vphantom {{{{V}^{\beta }}} {{{N}^{\beta }}}}} \right. \kern-0em} {{{N}^{\beta }}}}$ – средний молекулярный объем фазы β, $x_{k}^{\beta } \equiv {{N_{k}^{\beta }} \mathord{\left/ {\vphantom {{N_{k}^{\beta }} {{{N}^{\beta }}}}} \right. \kern-0em} {{{N}^{\beta }}}}$ – мольная доля компонента k и ${{N}^{\beta }}$ – общее число молекул всех сортов в фазе β:

Исключая $d{{\mu }_{j}}$ из (4) и (6), находим

С учетом (1) из (8) сразу видно, что при растворении газов в жидкости под действием давления на краевой угол оказывает влияние не только само давление, но и изменение состава жидкости при растворении газов. Лишь при условии закрепления химических потенциалов растворяемых газов из (8) следует простая формула

откуда сразу следует правило (краевой угол увеличивается с ростом давления, если адсорбция растворителя из жидкой фазы больше, чем из газовой фазы).

Для объемной фазы α капли в изотермических условиях уравнение Гиббса–Дюгема (5) предстает в виде

Поскольку, в соответствии с [3], мы рассматриваем хоть и малую, но макроскопическую каплю, капиллярная разность давлений ${{p}^{\alpha }} - {{p}^{\beta }}$ мала. Если ориентироваться на такие газы как компоненты воздуха, для которых изменение давления в опытах измеряется атмосферами (барами), то капиллярная разность давлений будет просто ничтожной (для капли воды размером 1 мм при 20°C около 0.003 бар) в сравнении с самими давлениями. Поэтому можем положить

Поделив теперь (11) на $x_{j}^{\alpha }$ и (6) на $x_{j}^{\beta }$, а затем, вычтя (6) из (11), находим

В этом приближении (в пренебрежении кривизной поверхности капли) уравнение (13) дает дополнительную связь между величинами, стоящими в правой части (8), где $d{{p}^{\beta }}$ можно теперь заменить на dp.

Условимся выделить один из компонентов газовой смеси (пусть это будет компонент 1) и, используя (14), запишем для него выражение

Подставив затем (14) в (8), получим

Если газовая смесь состоит только из одного компонента, выражение (15) упрощается к виду

Здесь хоть и фигурирует только давление в качестве единственной независимой переменной, строго учитывается как растворимость газа в жидкости, так и испарение жидкости в газовую фазу в зависимости от приложенного давления.

Рассмотрим форìмулу (16) более подробно. В практически важном случае воды и газов типа компонентов воздуха при обычных температурах можно считать растворимость газа малой. Например, коэффициент растворимости (литров газа на литр жидкости) даже диоксида углерода при температуре 20°C составляет 0.879, но ведь в литре газа молекул может быть на несколько порядков меньше, чем в литре жидкости. С другой стороны, вдали от критической температуры содержание испарившихся молекул жидкости в газовой фазе тоже мало. Таким образом, можно принять $x_{j}^{\alpha } \approx 1,$ $x_{j}^{\beta } \ll 1,$ $x_{1}^{\alpha } \ll 1,$ $x_{1}^{\beta } \approx 1,$ ${{{{v}^{\alpha }}} \mathord{\left/ {\vphantom {{{{v}^{\alpha }}} {x_{j}^{\alpha }}}} \right. \kern-0em} {x_{j}^{\alpha }}} \ll {{{{v}^{\beta }}} \mathord{\left/ {\vphantom {{{{v}^{\beta }}} {x_{j}^{\beta }}}} \right. \kern-0em} {x_{j}^{\beta }}},$ ${{x_{1}^{\alpha }} \mathord{\left/ {\vphantom {{x_{1}^{\alpha }} {x_{j}^{\alpha }}}} \right. \kern-0em} {x_{j}^{\alpha }}} \ll {{x_{1}^{\beta }} \mathord{\left/ {\vphantom {{x_{1}^{\beta }} {x_{j}^{\beta }}}} \right. \kern-0em} {x_{j}^{\beta }}}$ и

Подстановка (17) в (16) дает

Наконец, считая газ идеальным при ${{v}^{\beta }} = {{kT} \mathord{\left/ {\vphantom {{kT} p}} \right. \kern-0em} p}$ (k – постоянная Больцмана), можем записать (18) как

Знак правой части (18) определяется знаками и соотношениями адсорбций газа на представленных в системе поверхностях. Адсорбция газов на границе жидкость–газ изучена достаточно широко [10–12]. Если взять для конкретности системы диоксид углерода–вода и этан–циклогексан [10], то для них поверхностное натяжение уменьшается с давлением газа, и, значит, адсорбция газа положительна. Обращаясь к формуле (19), мы можем сказать, что в данном случае $\Gamma _{1}^{{\alpha \beta }}$ > 0. Что касается адсорбций на твердой подложке (в [10] использовалась нержавеющая сталь 316) $\Gamma _{1}^{{\alpha \gamma }}{\text{ и }}\Gamma _{1}^{{\beta \gamma }},$ для них сведений не имеется, но в ожидании этих данных мы можем провести следующие рассуждения. Прежде всего, необходимо отметить, что в отношении адсорбции межфазные поверхности твердого тела с жидкостью и газом ведут себя по-разному. В жидкости все пространство заполнено веществом. Поэтому, ввиду малой сжимаемости и примерной аддитивности молекулярных объемов, положительная адсорбция одного из компонентов влечет за собой отрицательную адсорбцию другого. Очевидно, положительно адсорбируется тот компонент, который сильнее притягивается подложкой в результате игры молекулярных сил. Будет ли это весьма полярная вода или диоксид углерода, молекулы которого вообще не обладают дипольным моментом? Вопрос не так прост с учетом химизма адсорбции CO₂ (образование угольной кислоты и ионов ${\text{CO}}_{3}^{{2 + }}),$ но если отдать предпочтение воде, то получим $\Gamma _{1}^{{\alpha \gamma }} < 0.$ Еще более очевидно это условие для газообразного этана в сочетании с жидким циклогексаном [10]. Оба вещества одной природы, но циклогексан сильнее притягивается подложкой просто потому, что его молекулы крупнее. Для него адсорбция положительна и, следовательно, для этана – отрицательна.

Совсем по-другому мыслится адсорбция из газовой фазы. Плотность последней настолько мала, что каждый из газов (или паров) смеси ведет себея почти независимо, как если бы он был один. Каждый газ притягивается подложкой и каждый адсорбируется положительно. В этом случае $\Gamma _{1}^{{\beta \gamma }} > 0.$ В сочетании с указанными значениями $\Gamma _{1}^{{\alpha \beta }} > 0$ и $\Gamma _{1}^{{\alpha \gamma }} < 0$ тогда получается, что все члены в правой части (19), а, значит, и сама правая часть, положительны. Отсюда следует, что с увеличением давления газа косинус краевого угла капли должен возрастать, а сам краевой угол – уменьшаться. Именно такая зависимость и наблюдается в эксперименте: при увеличении давления CO₂ от 1 до 9 бар наступающий краевой угол воды уменьшается от 77° до 44°, а при таком же изменении давления этана наступающий краевой угол циклогексана падает от 28° до 10° [10].

СЛУЧАЙ СИДЯЧЕГО ПУЗЫРЬКА

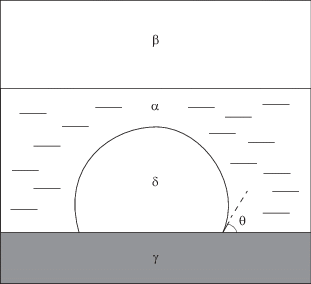
Представим теперь, что смесь газов под давлением растворяется в жидкости, а на стенке сосуда, в котором находится жидкость, появился пузырек. Чтобы перейти от рис. 1 к этому случаю, как можно меньше меняя обозначения фаз, вообразим, что капля (фаза α) разрослась в объемную жидкость, и пузырек находится внутри нее. В объеме пузырька находится новая фаза δ, а фаза β – по-прежнему исходная газовая смесь (рис. 2). Необходимость введения новой газовой фазы обосновывается следующим образом. Если бы фазы β и δ совпадали (т.е. состояли бы из одних и тех же компонентов), то при равновесии их температуры и химические потенциалы их компонентов были бы одинаковы. Но тогда, согласно уравнению Гиббса–Дюгема (5), и давления в этих фазах были бы одинаковы, а это невозможно в силу уравнения Лапласа. Таким образом, ситуация, изображенная на рис. 2, возможна при условии, что пузырек образуется еще одним газом, который отсутствует в фазе β и нерастворим в фазе α. По существу этот газ (типа гелия) играет роль газа–носителя в фазе δ.

Уравнение (3) в этом случае принимает вид

где суммирование производится по всем компонентам системы, исключая твердое тело, а поверхностное натяжение γ относится к границе αδ. Выделяя, как и раньше, основной компонент жидкости (растворитель газов) буквой j, а газ-носитель – буквой c, запишем (20) как где условие эквимолекулярности разделяющей поверхности в отношении компонента j учтено в виде $\Gamma _{j}^{{\alpha \delta }} = 0,$ а суммирование производится по всем компонентам растворяемой газовой смеси (фазы β). В уравнении (21) также учтено, что компонент c отсутствует в фазах α и γ, а потому и на границе αγ, так что величина $\Gamma _{с}^{{\alpha \gamma }}$ в уравнении (20) элиминируется.

Как и в уравнении (4), мы можем заменить $d{{\mu }_{j}}$ в уравнении (21) на dp (теперь условие (12) выполняется строго, поскольку граница между фазами α и β плоская) при помощи уравнения Гиббса–Дюгема (6). В результате получим

Как и условие (12), уравнение (13) теперь становится строгим:

и вместе с (22) образует систему уравнений для случая пузырька.

В простейшем варианте индивидуального газа (компонента 1) в фазе β из (23) находим

а (22) принимает форму

Выражения (16) для капли и (25) для пузырька различаются лишь наличием последнего слагаемого в (25), связанного с газом-носителем. Очевидно, производная dμ_c/dp положительна, поскольку при увеличении давления p пузырек сжимается и давление p^δ возрастает. Тогда роль последнего слагаемого определяется знаками и величинами адсорбций газа-носителя. Но если он совершенно инертен (не растворяется и не адсорбируется), то его адсорбция может быть только отрицательной. Поскольку же речь идет об адсорбции из газовой фазы, то эта отрицательная адсорбция не может не быть малой по абсолютной величине. Тогда обе адсорбции, фигурирующие в последнем слагаемом, а с ними и слагаемое в целом будут малыми. В пренебрежении этим слагаемым анализ, проведенный выше для капли, остается в силе и для пузырька.

ЗАКЛЮЧЕНИЕ

Данное исследование дополняет работы [1–3], где как экспериментально, так и теоретически было показано, что при приложении давления к жидкости с сидячим пузырьком краевой угол жидкости на линии трехфазного контакта возрастает. Теперь же, опять на основе и эксперимента, и термодинамической теории, мы убедились, что воздействием давления через газовую фазу в контакте с жидкостью достигается противоположный эффект: краевой угол уменьшается. Это объясняется растворимостью газов, которая неизбежно сопровождает повышение давления. При этом речь не идет о сильно растворимых газах (как, например, HCl в воде с образованием соляной кислоты). Если говорить о воде, то опыты ставились с CO₂ [10]. Мы же в своих оценках считали растворимость газа малой. И, тем не менее, эффект налицо.