Коллоидный журнал, 2021, T. 83, № 2, стр. 235-241

ВВЕДЕНИЕ

Во многих явлениях, связанных с межфазными границами твердое тело–газ и твердое тело–жидкость, большую роль играет образование на этих границах тонких пленок или прослоек [1, 2]. Сильная неоднородность внутри таких пленок приводит к возникновению расклинивающего давления [3–5]. В случае искривленных поверхностей пленки расклинивающее давление действует в противовес капиллярному давлению [3, 6] и может быть очень важным фактором при гетерогенном образовании частиц новой фазы [6–8]. Однако в отличие от плоских пленок или прослоек определение расклинивающего давления неоднозначно в случае искривленных межфазных поверхностей [9]. Использование изотерм расклинивающего давления для плоских пленок при рассмотрении пленок на смачиваемых сферических твердых частицах имеет свои пределы при уменьшении радиуса частиц. Эти пределы могут быть установлены только в рамках молекулярных моделей расклинивающего давления. Интерес также представляет молекулярное рассмотрение расклинивающего давления искривленных паровых прослоек вокруг лиофобных твердых частиц, для которых на сегодняшний день результатов недостаточно.

Исследованию соотношений для расклинивающего давления жидких пленок на лиофильных и паровых прослоек на лиофобных сферических твердых частицах в рамках градиентного приближения метода классического функционала плотности, вычислению и сравнению термодинамически и механически определенного расклинивающего давления для таких систем посвящено данное сообщение.

1. МЕТОД РАСЧЕТА

Эффективным методом для расчета равновесной структуры неоднородных флюидных систем служит метод классического функционала плотности (МКФП) [10, 11]. В рамках этого метода задается большой термодинамический потенциал системы ${{\Omega }^{{{\text{sf}}}}}\left[ \rho \right]$ как функционал локальной плотности $\rho $ числа молекул флюида; в объемной части этот флюид может быть в состоянии пара или жидкости.

Ниже будем использовать метод функционала плотности в градиентном приближении [12–16] совместно с моделью Карнахана–Старлинга для вклада твердых сфер и вкладом среднего поля для дальнодействующих сил [17]. Соответственно, большой термодинамический потенциал однокомпонентного флюида с жидкой пленкой или паровой прослойкой вблизи сферической твердой частицы радиуса ${{R}_{{\text{p}}}}$ в заданном объеме $V$ и при заданном химическом потенциале $\mu $ определим [18–22] как

Здесь $\vec {r}$ – радиус-вектор из центра частицы в точку системы, ${{k}_{{\text{B}}}}$ – постоянная Больцмана, $T$ – абсолютная температура системы, ${{\lambda }_{{{\text{th}}}}} \equiv \hbar \sqrt {{{2\pi } \mathord{\left/ {\vphantom {{2\pi } {(m{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {(m{{k}_{{\text{B}}}}T}})} $ – тепловая длина волны де Бройля ($\hbar $ – постоянная Планка, $m$ – масса молекулы флюида), $\eta \equiv {{\pi {{d}^{3}}\rho } \mathord{\left/ {\vphantom {{\pi {{d}^{3}}\rho } 6}} \right. \kern-0em} 6}$ – безразмерная молекулярная плотность флюида ($d$ – диаметр молекулы в модели твердых сфер), $a$ – параметр межмолекулярного притяжения во флюиде в приближении среднего поля, $C = 14{{\sigma }^{5}}{{k}_{{\text{B}}}}T$ [23] – параметр, связанный с поверхностным натяжением $\gamma _{\infty }^{{}}$ на плоской поверхности раздела жидкой и газовой фаз, $\sigma \equiv {{\left( {{\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0em} 6}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}d,$ $\mu $ – химический потенциал молекул флюида. Величина ${{w}_{{{\text{pf}}}}}$ является полным потенциалом взаимодействия сферической твердой частицы (с молекулярной плотностью ${{\rho }_{{\text{p}}}}$) с молекулой флюида в точке $\vec {r}{\text{:}}$где ${{\varepsilon }_{{{\text{pf}}}}}$ – энергетический параметр леннард-джонсовского взаимодействия молекулы твердой частицы и молекулы флюида.

Первым шагом в решении поставленной в данном сообщении задачи является нахождение равновесного профиля плотности флюида ${{\rho }^{{{\text{(e)}}}}}$ из условия стационарности ${{\left. {{{\delta {{\Omega }^{{{\text{sf}}}}}} \mathord{\left/ {\vphantom {{\delta {{\Omega }^{{{\text{sf}}}}}} {\delta \rho }}} \right. \kern-0em} {\delta \rho }}} \right|}_{{{{{\rho }}^{{{\text{(e)}}}}}}}} = 0.$ Хотя среди равновесных профилей плотности могут быть и несферические профили, отвечающие образованию сидячих капель или пузырьков [11], далее будем искать только сферически симметричные решения с плотностью ${{\rho }^{{{\text{(e)}}}}}\left( r \right),$ описывающие формирование концентрических пленок или прослоек. Очевидно, что существование таких решений требует не только сферичности твердой частицы, но и существенных ограничений на ее смачивание или несмачивание, характеризуемое в нашей модели потенциала ${{\Omega }^{{{\text{sf}}}}}\left[ \rho \right]$ безразмерным отношением $\varepsilon \equiv {{4\pi {{\varepsilon }_{{{\text{pf}}}}}{{\rho }_{{\text{p}}}}{{\sigma }^{3}}} \mathord{\left/ {\vphantom {{4\pi {{\varepsilon }_{{{\text{pf}}}}}{{\rho }_{{\text{p}}}}{{\sigma }^{3}}} {5a\rho _{\infty }^{{\text{L}}}}}} \right. \kern-0em} {5a\rho _{\infty }^{{\text{L}}}}},$ где $\rho _{\infty }^{{\text{L}}}$ – плотность числа молекул жидкости при $\mu = {{\mu }_{\infty }}$ (${{\mu }_{\infty }}$ – химический потенциал молекул флюида при равновесии жидкости и пара при плоской межфазной поверхности; здесь и далее нижний индекс $\infty $ характеризует величины, определенные при ${{\mu }_{\infty }}$).

Подстановка (1) в условие стационарности дает нелинейное дифференциальное уравнение

с краевыми условиями ${{\left. {{{\rho }^{{{\text{(e)}}}}}\left( r \right)} \right|}_{{{{R}_{{\text{p}}}} + \delta }}} = 0$ и ${{\left. {{{\rho }^{{{\text{(e)}}}}}\left( r \right)} \right|}_{{r \to \infty }}} = {{\rho }^{{{\text{G,L}}}}}$ [20–22] (${{\rho }^{{\text{G}}}}$ и ${{\rho }^{{\text{L}}}}$ – плотности числа молекул пара и, соответственно, жидкости при заданном значении химического потенциала $\mu $). Здесь и далее присутствие пары верхних индексов означает, что первый верхний индекс относится к случаю жидкой пленки, второй индекс – к случаю паровой прослойки. Выбор точки ${{R}_{{\text{p}}}} + \delta ,$ в которой ставится граничное условие со стороны твердой частицы, допускает определенный произвол. Учет вклада твердых сфер в потенциал взаимодействия делает невозможным приближение молекулы к твердой стенке ближе, чем на радиус молекулы ${d \mathord{\left/ {\vphantom {d {2,}}} \right. \kern-0em} {2,}}$ поэтому выбор $\delta = {d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}$ является логичным. Однако любой другой выбор значения $0 \leqslant \delta \leqslant {d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}$ не должен заметно менять решение задачи. В нашем случае конкретный выбор значения $\delta $ будет определяться численным методом решения задачи.

При известном равновесном профиле плотности ${{\rho }^{{{\text{(e)}}}}}\left( r \right)$ радиус ${{R}_{{{\text{em}}}}}$ эквимолекулярной разделяющей поверхности концентрической жидкой пленки или паровой оболочки вокруг твердой частицы радиуса ${{R}_{{\text{p}}}}$ равен [19–22]:

Второй шаг в решении поставленной в данном сообщении задачи связан с нахождением тангенциальной и нормальной компонент тензора давления по найденным профилям плотности и толщинам пленок или прослоек. В сферически симметричном случае тангенциальная компонента ${{p}_{{\text{T}}}}$ локального тензора давления в системе совпадает с взятой со знаком минус интегральной плотностью большого термодинамического потенциала в (1). Используя вытекающую из локального условия механического равновесия ${{d\left( {{{p}_{{\text{N}}}}\left( r \right){{r}^{2}}} \right)} \mathord{\left/ {\vphantom {{d\left( {{{p}_{{\text{N}}}}\left( r \right){{r}^{2}}} \right)} {d{{r}^{2}}}}} \right. \kern-0em} {d{{r}^{2}}}}$ = ${{p}_{{\text{T}}}}\left( r \right)$ связь между нормальной ${{p}_{{\text{N}}}}$ и тангенциальной ${{p}_{{\text{T}}}}$ компонентами тензора давления [24], получаем где $L$ – расстояние от центра твердой частицы, при котором уже выполнено равенство ${{p}_{{\text{N}}}}(L) = {{p}_{{\text{T}}}}(L) = {{p}^{{{\text{L,G}}}}},$ ${{p}^{{\text{G}}}}$ и ${{p}^{{\text{L}}}}$ – объемные значения давления пара и соответственно жидкости при заданном значении химического потенциала $\mu .$

Согласно [25, 26] условие механического равновесия для сферической смачивающей жидкой пленки или паровой прослойки на сферической твердой частице можно записать в виде

где $\gamma _{{{\text{em}}}}^{{}}$ – поверхностное натяжение для эквимолекулярной разделяющей поверхности, ${{R}_{{{\text{em}}}}}$ – радиус эквимолекулярной разделяющей поверхности при заданном химическом потенциале, радиус ${{r}_{{\text{i}}}}$ соответствует границе вблизи поверхности твердого тела, где пленка или прослойка начинается.

Согласно [27] большой термодинамический потенциал ${{\Omega }^{{{\text{sf}}}}}$ системы со сферической жидкой пленкой или паровой прослойкой может быть представлен из термодинамических соображений как

где величина $\Pi \left( h \right)$ имеет смысл расклинивающего давления пленки или прослойки, определенного термодинамически. Из (7) следует условие равновесия пленки или прослойки в виде [27] Из (6) и (8) видим, что величины можно считать механическим и термодинамическим определениями расклинивающего давления сферической пленки или прослойки. Очевидно, что для жидких пленок и паровых прослоек должно иметь место равенство ${{{\Pi }}_{{\text{M}}}} = {{{\Pi }}_{{\text{T}}}}.$ В пределе плоской поверхности твердого тела и плоской жидкой пленки или паровой прослойки оба определения, с учетом постоянства нормальной компоненты тензора давления при плоской межфазной поверхности, совпадают с известным определением расклинивающего давления в [3, 4].

2. РЕЗУЛЬТАТЫ РАСЧЕТА

Уравнение (3) решалось при различных значениях химического потенциала $\mu $ методом стрельбы с использованием метода Рунге–Кутты решения начальной задачи. Начальные значения плотности ${{\rho }^{{{\text{(e)}}}}}\left( L \right) = {{\rho }^{{{\text{G,L}}}}}$ задавались при достаточно больших значениях $L\sim (20{\kern 1pt} --{\kern 1pt} 30)\sigma .$ Начальные значения производных ${{\left. {{{d{{\rho }^{{{\text{(e)}}}}}\left( r \right)} \mathord{\left/ {\vphantom {{d{{\rho }^{{{\text{(e)}}}}}\left( r \right)} {dr}}} \right. \kern-0em} {dr}}} \right|}_{{r = L}}}$ подбирались таким образом, чтобы удовлетворить второму граничному условию ${{\left. {{{\rho }^{{{\text{(e)}}}}}\left( r \right)} \right|}_{{{{R}_{{\text{p}}}} + \delta }}} = 0$ при $0 \leqslant \delta \leqslant {d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}.$ При слишком малых значениях $\delta \leqslant {d \mathord{\left/ {\vphantom {d 4}} \right. \kern-0em} 4},$ однако, численных решений получить не удавалось, что, по-видимому, определяется ограничениями используемого метода. Для контроля точности те же профили были вычислены “обратной стрельбой”, т.е. решением начальной задачи для $r = {{R}_{{\text{p}}}} + \delta $ и тех же значений $\delta $ и ${{\rho }^{{{\text{(e)}}}}}\left( {{{R}_{{\text{p}}}} + \delta } \right),$ что были получены ранее. Фактически и подходящие значения L выбирались путем предварительной оценки поведения решений начальной задачи для уравнения (3) с подходящими начальными условиями при $r \approx {{R}_{{\text{p}}}} + {d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}.$

Были взяты следующие значения параметров: $T = 90$ K, πd ³/6 = 16.22 × 10^–30 м³, σ = (πd ³/6)^1/3 = = 2.53 × 10^–10 м, a = 3.58 × 10^–49 Дж м³, которым соответствовали μ_∞ = –1.539 × 10^–20 Дж, $\eta _{\infty }^{{\text{L}}} = {{\sigma }^{3}}{{\rho }^{{\text{L}}}}\left( {{{\mu }_{\infty }}} \right) = 0.408,$ $\eta _{\infty }^{{\text{G}}} = {{\sigma }^{3}}{{\rho }^{{\text{G}}}}\left( {{{\mu }_{\infty }}} \right) = 0.00296,$ ${{\gamma }_{\infty }} = 0.0119$ Н/м, ${{R}_{{\text{p}}}} = 10\sigma .$ В случае формирования жидкой пленки были взяты ρ_p = 26.6 × 10²⁷ м^–3 (как для кварца), ${{\varepsilon }_{{{\text{pf}}}}} = 5{{{a \mathord{\left/ {\vphantom {a \sigma }} \right. \kern-0em} \sigma }}^{3}}$ и значения $\mu > {{\mu }_{\infty }}$ (метастабильный пересыщенный пар). В случае паровой прослойки были взяты ρ_p = 1.07 × 10²⁷ м^–3 (как для парафина), ${{\varepsilon }_{{{\text{pf}}}}} = {{{{0.01a} \mathord{\left/ {\vphantom {{0.01a} \sigma }} \right. \kern-0em} \sigma }}^{3}}$ и значения $\mu < {{\mu }_{\infty }}$ (метастабильная растянутая жидкость).

На рис. 1 приведены найденные безразмерные равновесные профили плотности ${{\eta }^{{{\text{(e)}}}}}\left( r \right) \equiv $ $ \equiv {{\pi {{d}^{3}}{{\rho }^{{{\text{(e)}}}}}\left( r \right)} \mathord{\left/ {\vphantom {{\pi {{d}^{3}}{{\rho }^{{{\text{(e)}}}}}\left( r \right)} 6}} \right. \kern-0em} 6}$ в зависимости от ${{\tilde {r} \equiv r} \mathord{\left/ {\vphantom {{\tilde {r} \equiv r} \sigma }} \right. \kern-0em} \sigma }$ при указанных в поле рисунка значениях безразмерного сдвига химического потенциала $b \equiv {{\left( {\mu - {{\mu }_{\infty }}} \right)} \mathord{\left/ {\vphantom {{\left( {\mu - {{\mu }_{\infty }}} \right)} {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}.$ Видим, что решения уравнения (3), отвечающие концентрическим пленкам и прослойкам, действительно, существуют при выбранных значениях параметров. Более того, расчеты показали, что при ${{\mu }_{\infty }} < \mu < \mu _{{{\text{th}}}}^{{\text{G}}}$ в случае жидких пленок и при $\mu _{{{\text{th}}}}^{{\text{L}}} < \mu < {{\mu }_{\infty }}$ в случае паровых прослоек таких решений два при каждом значении $\mu .$ При этом первое из них отвечает устойчивому равновесному профилю (локальному минимуму функционала ${{\Omega }^{{{\text{sf}}}}}\left[ \rho \right]$ в пространстве профилей $\rho $), а второе – неустойчивому равновесному профилю (седловой точке функционала ${{\Omega }^{{{\text{sf}}}}}\left[ \rho \right]$ в пространстве профилей $\rho $). Аналогичная ситуация хорошо известна для нуклеации на заряженных частицах [28–31]. В случае образования капель на смачиваемых ядрах конденсации ранее подобное поведение было связано в [7, 8] с изотермами расклинивающего давления в жидких пленках. Очевидно, что капельки и паровые прослойки, в которых профиль плотности соответствует минимуму ${{\Omega }^{{{\text{sf}}}}},$ будут долгоживущими.

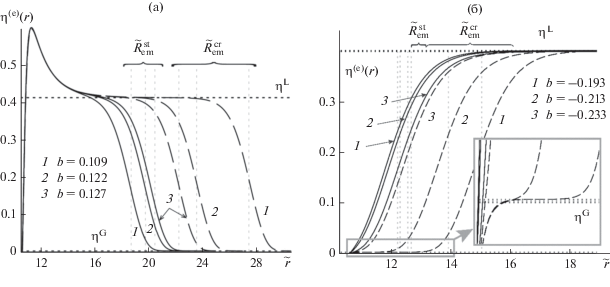
Заметим, что пороговые значения $\mu _{{{\text{th}}}}^{{\text{G}}}$ и $\mu _{{{\text{th}}}}^{{\text{L}}}$ зависят от радиуса частицы и других параметров системы. При взятых для построения рис. 1 параметрах имеем ${{b_{{{\text{th}}}}^{{\text{G}}} \equiv \left( {\mu _{{{\text{th}}}}^{{\text{G}}} - {{\mu }_{\infty }}} \right)} \mathord{\left/ {\vphantom {{b_{{{\text{th}}}}^{{\text{G}}} \equiv \left( {\mu _{{{\text{th}}}}^{{\text{G}}} - {{\mu }_{\infty }}} \right)} {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}$ = 0.127 и ${{b_{{{\text{th}}}}^{{\text{L}}} \equiv \left( {\mu _{{{\text{th}}}}^{{\text{L}}} - {{\mu }_{\infty }}} \right)} \mathord{\left/ {\vphantom {{b_{{{\text{th}}}}^{{\text{L}}} \equiv \left( {\mu _{{{\text{th}}}}^{{\text{L}}} - {{\mu }_{\infty }}} \right)} {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}$ = –0.233. Наличие пика на профиле плотности в жидкой пленке вблизи поверхности твердой частицы на рис. 1а показывает, что взятое значение ${{\varepsilon }_{{{\text{pf}}}}} = 5{{{a \mathord{\left/ {\vphantom {a \sigma }} \right. \kern-0em} \sigma }}^{3}}$ действительно отвечает хорошему смачиванию вещества твердой частицы жидкой фазой. Соответственно выбор ${{\varepsilon }_{{{\text{pf}}}}} = {{{{0.01a} \mathord{\left/ {\vphantom {{0.01a} \sigma }} \right. \kern-0em} \sigma }}^{3}}$ должен с запасом обеспечивать лиофобность твердой частицы. С уменьшением параметра ${{\varepsilon }_{{{\text{pf}}}}}$ для случая пересыщенного пара и его увеличением в случае растянутой жидкости равновесные решения уравнения (3) в виде концентрических профилей плотности исчезают. По-видимому [11], здесь происходит переход к решениям в виде сидячих капелек или пузырьков.

Рассчитанные профили плотности были подставлены в вытекающее из (1) соотношение для ${{p}_{{\text{T}}}}(r)$ и далее в формулу (5) для ${{p}_{{\text{N}}}}(r).$ Результаты расчета профилей нормальной компоненты ${{p}_{{\text{N}}}}(r)$ тензора давления показаны на рис. 2.

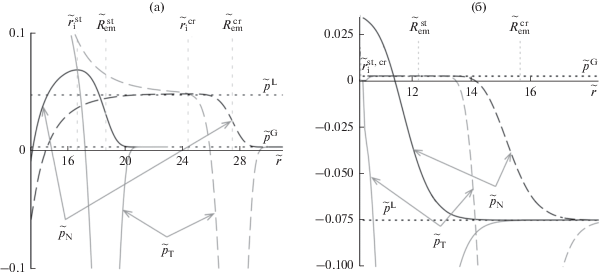
Как следует из рис. 2, в качестве радиуса ${{r}_{{\text{i}}}}$ границы пленки или прослойки вблизи поверхности твердого тела разумно выбрать положение максимума нормальной компоненты тензора давления. Рисунок 2a показывает, что в концентрической с частицей капельке максимум нормальной компоненты давления расположен на некотором отдалении от поверхности частицы, ближе к середине пленки, причем в точке ${{r}_{{\text{i}}}}$ значения ${{p}_{{\text{N}}}}$ и ${{p}_{{\text{T}}}}$ очень близки, тогда как из рис. 2б видим, что в случае паровой прослойки максимум расклинивающего давления достигается при ${{r}_{{\text{i}}}} = {{R}_{{\text{p}}}} + \delta ,$ но значения ${{p}_{{\text{N}}}}$ и ${{p}_{{\text{T}}}}$ заметно различаются. Такое различие можно объяснить тем, что в случае капли на лиофильной частице поверхностные силы на границе жидкость–частица и на границе жидкость–пар имеют примерно одинаковый радиус действия, следовательно, область перекрытия поверхностных слоев располагается примерно посередине пленки. В случае же паровой оболочки на лиофобной частице именно вблизи поверхности частицы свойства прослойки наиболее сильно отличаются от свойств жидкости.

С увеличением отклонения химического потенциала от значения ${{\mu }_{\infty }}$ толщины ${{h}_{{{\text{em}}}}} \equiv {{R}_{{{\text{em}}}}} - {{R}_{{\text{p}}}}$ жидкой пленки (при $\mu > {{\mu }_{\infty }}$) и паровой прослойки (при $\mu < {{\mu }_{\infty }}$) возрастают, а максимальное значение нормальной компоненты тензора давления увеличивается. С усилением гидрофильности (с ростом параметра ${{\varepsilon }_{{{\text{pf}}}}}$) максимум ${{p}_{{\text{N}}}}(r)$ в жидкой пленке растет. В паровой прослойке максимум ${{p}_{{\text{N}}}}(r)$ растет при увеличении гидрофобности (уменьшении ${{\varepsilon }_{{{\text{pf}}}}}$).

Чтобы вычислить механическое расклинивающее давление, в формуле для ${{\Pi }_{{\text{M}}}}$ положим соответствующие пленкам и прослойкам значения ${{r}_{{\text{i}}}},$ $\max {{p}_{{\text{N}}}}\left( r \right),$ ${{p}^{{\text{L}}}},$ ${{p}^{{\text{G}}}}$ и подставим ранее найденные с помощью (4) значения ${{R}_{{{\text{em}}}}}.$ Результаты расчетов при четырех значениях радиуса ${{R}_{{\text{p}}}}$ центральной твердой частицы представлены на основном поле рис. 3. Наибольший радиус ${{R}_{{\text{p}}}} = 60\sigma $ практически соответствует пределу плоской твердой стенки.

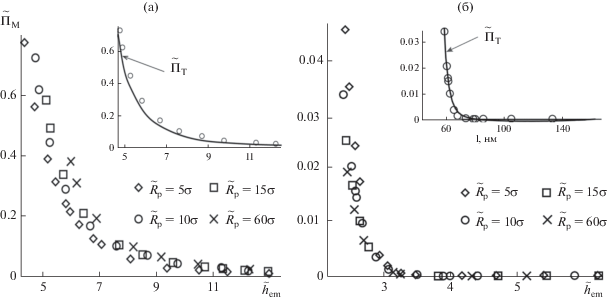
При вычислении термодинамического расклинивающего давления в случае жидких пленок воспользуемся итерационной процедурой. На первом шаге вычислим ${{{\Pi }}_{{\text{T}}}}$ по формуле (10) при ${{\gamma }_{{{\text{em}}}}} = {{\gamma }_{\infty }}.$ В случае капель присутствие непроницаемой поверхности ядра конденсации существенно влияет на плотность флюида вблизи такой поверхности, что видно по пику на рис. 1а. Это влияние даже больше на нормальную и тангенциальную компоненту тензора вблизи поверхности твердого ядра. Исключим вклад, связанный с присутствием сторонней частицы и окружающей ее сольватной оболочки, и будем интегрировать большой термодинамический потенциал ${{\Omega }^{{{\text{sf}}}}}$ не по всему объему $V,$ а начиная с радиуса ${{r}_{{\text{i}}}}$. Исключение области интегрирования от ${{R}_{{\text{p}}}}$ до ${{r}_{{\text{i}}}}$ для ${{\Omega }^{{{\text{sf}}}}}$в левой части (7) приводит к замене радиуса ${{R}_{{\text{p}}}}$ на ${{r}_{{\text{i}}}}$ в первом слагаемом в правой части (7). Полученную зависимость ${\Pi }_{{\text{T}}}^{{(0)}}(h)$ подставляем в выражение (7) и находим значение $\gamma _{{{\text{em}}}}^{{(1)}},$ затем подставляем $\gamma _{{{\text{em}}}}^{{(1)}}$ в (10) и вновь находим зависимость ${\Pi }_{{\text{T}}}^{{(1)}}(h).$ На вставке на рис. 3а приведена вторая итерация ${\Pi }_{{\text{T}}}^{{(2)}}(h).$ Из расчета видно, что результат итераций достаточно быстро сходится.

Чтобы вычислить термодинамически определенное расклинивающее давление паровой прослойки на лиофобной частице, исключим слагаемое ${{2{{\gamma }_{{{\text{em}}}}}} \mathord{\left/ {\vphantom {{2{{\gamma }_{{{\text{em}}}}}} {{{R}_{{{\text{em}}}}}}}} \right. \kern-0em} {{{R}_{{{\text{em}}}}}}}$ в формуле для ${{{\Pi }}_{{\text{T}}}}$ с помощью соотношения (7). В итоге получаем интегральное уравнение на ${{{\Pi }}_{{\text{T}}}}{\text{:}}$

где ${{h}_{{{\text{em}}}}} \equiv {{R}_{{{\text{em}}}}} - {{R}_{{\text{p}}}}$ – толщина сферической прослойки и Для каждого значения ${{R}_{{{\text{em}}}}}$ функция $q({{R}_{{{\text{em}}}}})$ может быть вычислена поточечно. Уравнение (11) можно решать путем его сведения к обыкновенному дифференциальному уравнению, умножив обе части (11) на ${{R}_{{{\text{em}}}}}$ и продифференцировав по ${{h}_{{{\text{em}}}}}.$ Результат решения и сравнение зависимостей ${{{\Pi }}_{{\text{T}}}}$ и ${{\Pi }_{{\text{M}}}}$ от толщины ${{h}_{{{\text{em}}}}} = {{R}_{{{\text{em}}}}} - {{R}_{{\text{p}}}}$ в случае образования пленки или прослойки приведены на вставке на рис. 3б.

Как следует из рис. 3а и 3б, расклинивающее давление в сферической концентрической капле вокруг лиофильной частицы убывает, а в концентрическом пузырьке на лиофобной частице – растет с уменьшением радиуса лиофобной частицы. Соответственно, расклинивающее давление в плоской жидкой пленке заданной толщины – наибольшее из возможных при заданной лиофильности твердой частицы, а в плоской паровой прослойке – наименьшее при заданной лиофобности частицы. Соответствие механического и термодинамического определений расклинивающего давления для сферических пленок и прослоек достаточно хорошее.

ЗАКЛЮЧЕНИЕ

Мы показали в рамках единого подхода, что градиентный метод классического функционала плотности позволяет явно рассчитать равновесные локальные профили плотности, компоненты тензора давления и толщины тонких концентрических прослоек между лиофильной или лиофобной твердой поверхностью и соответственно газовой или жидкой фазой. Эти прослойки неизотропны, и в них существует расклинивающее давление, для которого получены зависимости от толщины прослоек. При наличии капиллярного давления внутри прослоек расклинивающее давление ему противодействует и приводит к появлению устойчивых долгоживущих капелек вокруг лиофильных твердых частиц и пузырьков вокруг лиофобных частиц. Показано согласие механического и термодинамического определений расклинивающего давления в сферической прослойке.