Коллоидный журнал, 2021, T. 83, № 3, стр. 277-292
Влияние гравитации на фильтрацию субмикронных аэрозолей тяжелых металлов
В. А. Кирш 1, 2, *, А. А. Кирш 1
1 Национальный исследовательский центр “Курчатовский институт”
123182 Москва, пл. Академика Курчатова, 1, Россия
2 Институт физической химии и электрохимии им. А.Н. Фрумкина РАН
11907 Москва, Ленинский просп., 31, Россия
* E-mail: va_kirsch@mail.ru
Поступила в редакцию 07.12.2020
После доработки 16.12.2020
Принята к публикации 21.12.2020
Аннотация
Исследовано влияние гравитации на осаждение субмикронных аэрозольных частиц с высокой плотностью в волокнистых фильтрах из вертикального и горизонтального (относительно направления вектора силы тяжести) потоков газа при малых числах Рейнольдса, $\operatorname{Re} \ll 1.$ На основе численного решения уравнений Стокса и конвективной диффузии рассчитаны коэффициенты захвата сферических частиц конечного размера модельными фильтрами с двух- и трехмерным полем течения и реальными фильтрами в зависимости от размера и плотности частиц, скорости и направления потока и с учетом осаждения частиц на обратной стороне волокон в восходящих потоках. Результаты расчетов подтверждаются проведенными экспериментами по осаждению субмикронных сферических серебряных частиц в сетках и волокнистых фильтрах.
1. ВВЕДЕНИЕ
Проблема высокоэффективного улавливания субмикронных аэрозольных частиц с высокой плотностью обусловлена необходимостью соблюдения санитарных норм при работе с аэрозолями металлов. Эта проблема особенно актуальна из-за присутствия таких частиц в воздухе на предприятиях с ядерными технологиями [1, 2]. Фильтрация субмикронных тяжелых аэрозолей исследована недостаточно, поскольку всегда считалось, что они осаждаются эффективно и нерешенных задач в этой области нет. Действительно, при обычной скорости тяжелые частицы осаждаются даже более эффективно, чем частицы с малой плотностью, вследствие дополнительного инерционного механизма осаждения. Однако если средняя скорость течения аэрозоля через фильтрующий материал мала, $\left\langle u \right\rangle \ll 1$ cм/с, как в случае пассивных аварийных фильтров, в которых прокачка воздуха может осуществляться за счет естественной тяги, то гравитация и направление потока будут определять эффективность осаждения частиц.
Влияние гравитации на улавливание субмикронных частиц было обнаружено при измерении проскока аэрозолей через фильтр при изменении направления потока. Оказалось, что в потоке, направленном через фильтр снизу вверх, проскок мелких броуновских частиц больше, чем в потоке, направленном сверху вниз, причем это различие возрастает с уменьшением скорости потока [3]. Вклад гравитации в эффективность осаждения частиц может быть значительным даже при фильтрации аэрозолей с частицами небольшой плотности [4].
Для учета гравитации были получены аналитические формулы, но только в качестве поправок к коэффициенту захвата частиц конечного размера, без учета диффузии и инерции частиц [5]. Коэффициент захвата $\eta $ по определению равен доле частиц, осаждающихся из набегающего потока на единице длины волокна. Он связан с эффективностью фильтра $E$ и коэффициентом проскока ${n \mathord{\left/ {\vphantom {n {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}}$ при осаждении частиц радиуса ${{r}_{{\text{p}}}}$ в фильтре толщиной $H$ и плотностью упаковки $\alpha ,$ состоящем из волокон радиуса $a,$ следующей формулой:
(1)
$E = 1 - {n \mathord{\left/ {\vphantom {n {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}} = 1 - \exp \left( { - 2alH\eta } \right),$(2)
${{\eta }_{{{\text{RG}}}}} = {{\eta }_{{\text{R}}}} + {{\eta }_{{\text{G}}}} = {{{{R}^{2}}} \mathord{\left/ {\vphantom {{{{R}^{2}}} {{{k}_{1}}}}} \right. \kern-0em} {{{k}_{1}}}} \pm G(1 + R),$(4)
${{\eta }_{{{\text{RG}}}}} = {{\eta }_{{\text{R}}}} + 0.5{{G}^{2}}{{\left( {1 + R} \right)}^{2}}\eta _{{\text{R}}}^{{ - 1}}.$(5)
${{k}_{1}} = \alpha - 0.5\ln \alpha - 0.25{{\alpha }^{2}} - 0.75 + \tau \left( {1 - \alpha } \right){\text{Kn,}}$Основным механизмом улавливания субмикронных аэрозолей при обычной малой скорости потока через фильтр является диффузионное смещение частиц с линий тока вблизи волокон. Коэффициент захвата безынерционных частиц конечного размера с учетом влияния соседних волокон, эффекта зацепления и слабого влияния гравитации можно оценить по формуле [5]
(6)
$\eta = {{\eta }_{{\text{D}}}} + {{\eta }_{{\text{R}}}} + {{\eta }_{{{\text{DR}}}}} + {{\eta }_{{\text{G}}}},$(7)
${{\eta }_{{\text{w}}}} = K{{\left( {{{{{A}_{7}}Cr_{{\text{p}}}^{2}} \mathord{\left/ {\vphantom {{{{A}_{7}}Cr_{{\text{p}}}^{2}} {{{a}^{5}}U\mu k_{1}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}} \right. \kern-0em} {{{a}^{5}}U\mu k_{1}^{{{5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0em} 2}}}}}} \right)}^{{{2 \mathord{\left/ {\vphantom {2 7}} \right. \kern-0em} 7}}}},$При сильном влиянии гравитации сумма коэффициентов захвата может быть меньше, чем коэффициент захвата за счет гравитации, и тогда частицы из восходящего потока, согласно оценкам по (6), не улавливаются [9–11]. А относительно недавно сообщалось [13], что найдены условия, при которых в результате действия гравитации и инерции осаждения частиц в фильтре из потока вообще не происходит. Авторы [13] не учли эффект зацепления, т.е. собственный размер частиц, и сделали оценки при столь малых значениях числа Стокса (вплоть до ${\text{Stk}}$ ∼ 10–5), при которых инерционного смещения частиц с линий тока и, следовательно, инерционного осаждения быть не может. При этом они цитируют монографию [3], в которой Фукс объяснил, почему некорректно рассматривать инерционное осаждение точечных частиц без учета их конечного размера. Добавим, что инерционное осаждение частиц конечного размера в стоксовом потоке с учетом влияния гравитации и сил Ван-дер-Ваальса было впервые подробно рассмотрено в [14, 15].
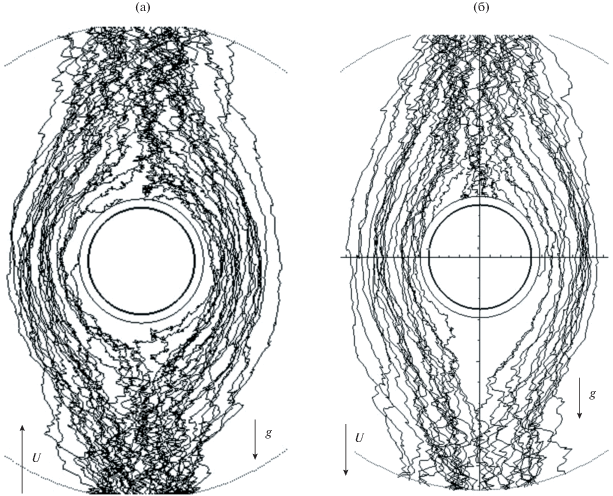
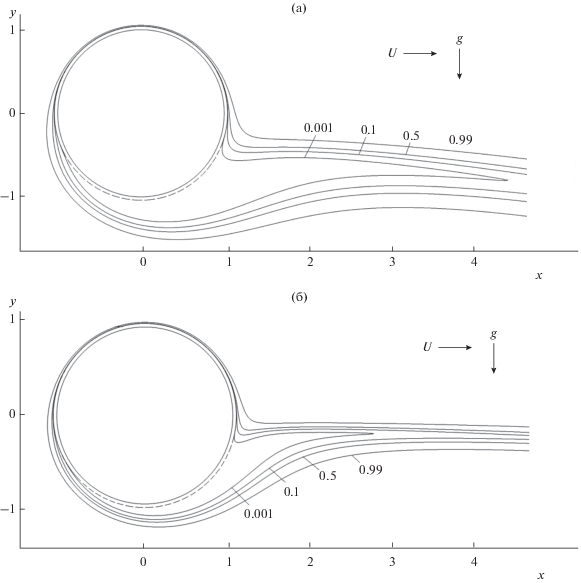
При расчете осаждения безынерционных тяжелых частиц следует учитывать, что при движении по линиям тока вверх и вниз время их пребывания около волокна разное. При движении частиц снизу вверх оно больше, чем при движении сверху вниз и соответственно бóльшим должно быть диффузионное осаждение и заметнее роль сил Ван-дер-Ваальса. Эффективность осаждения при течении снизу вверх, действительно, должна резко падать, так как частицы не достигают лобовой поверхности волокна, но некоторая доля частиц, не учитываемая в (6), осаждается на обратной стороне волокна, что и иллюстрирует рис. 1. На нем показаны траектории тяжелых броуновских частиц около волокна в коаксиальной ячейке, рассчитанные методом броуновской динамики. Количество частиц на входе в ячейку одинаковое. Видно, что в обоих случаях осаждение происходит на верхней половине волокна. При этом частицы в восходящем потоке обходят волокно и осаждаются на него сверху. Подчеркнем, что стохастический метод броуновской динамики пригоден лишь для визуализации траекторий броуновских частиц, но неприменим для точного расчета коэффициента захвата или коэффициента проскока частиц. По этой причине далее в работе мы используем континуальный подход и устойчивую конечно-разностную схему численного решения уравнения конвекции–диффузии [16].
Рис. 1.
Траектории частиц в восходящем (а) и нисходящем (б) потоках в ячейке Кувабары при следующих значениях параметров: ${{r}_{{\text{p}}}}$ = 0.5 мкм, $a$ = 5 мкм, $U$ = 1 см/с, $\alpha $ = 0.05, $\rho $ = 10 г/см3; число траекторий $M$ = 50.
Данная статья посвящена исследованию гравитационного осаждения субмикронных броуновских частиц в волокнистом фильтре из стоксова потока воздуха при малых числах Рейнольдса, $\operatorname{Re} \ll 1.$ В первой части приводятся результаты численных расчетов осаждения частиц на волокна из вертикальных потоков сверху вниз и снизу вверх. В качестве модельного фильтра используется изолированный эквидистантный ряд параллельных круговых волокон или ячеечная модель, которые отражают основные свойства реального фильтра. Во второй части проведено сравнение результатов расчета для ряда волокон и модельной сетки из скрещенных волокон с данными экспериментов по осаждению субмикронных частиц серебра в реальных стекловолокнистых и сеточных фильтрах при разных направлениях потока.
2. РАСЧЕТ ОСАЖДЕНИЯ ТЯЖЕЛЫХ ЧАСТИЦ НА ВОЛОКНО
Осаждение тяжелых частиц будем рассчитывать при малой скорости течения аэрозолей при $G < 1$ и ${\text{Stk}} \ll 1,$ т.е. в условиях, когда инерцией частиц можно пренебречь. Это накладывает ограничение на выбор скорости потока U, радиуса волокон a, радиуса частиц ${{r}_{{\text{p}}}}$ и их плотности ρ. Перенос броуновских безынерционных частиц в пространственно неоднородном поле скоростей ${\mathbf{u}}$ и сил ${\mathbf{f}}$ включает в себя диффузию частиц, их конвективный перенос и миграцию в поле внешних сил. Соответствующее выражение для вектора плотности потока частиц имеет вид
(8)
${\mathbf{j}}* = - D\nabla {\text{*}}n{\text{*}} + {\mathbf{u}}{\text{*}}n{\text{*}} + B{\mathbf{f}}n{\kern 1pt} *,$В полярных координатах скорость частицы в поле внешних сил равна ${{{v}}_{r}} = {{u}_{r}} - G\cos \left( {\chi - \theta } \right)$ + + $B{{U}^{{ - 1}}}{{f}_{{\text{w}}}},$ ${{{v}}_{\theta }} = {{u}_{\theta }} - G\sin \left( {\chi - \theta } \right),$ где $\chi $ – угол между векторами скорости потока перед фильтром $U{\mathbf{i}}$ и скорости седиментации частиц, ${\mathbf{i}}$ – единичный вектор в направлении оси $Ox.$ Угол $\chi $ = 0 соответствует нисходящему, $\chi $ = $\pi $ – восходящему, $\chi $ = = ${\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$ – горизонтальному потоку.
Для силы ван-дер-ваальсова притяжения используем формулы для шара и плоскости, применимые при $R$ < 1, когда кривизной волокна можно пренебречь [17, 18]:
(10)
$f_{{\text{6}}}^{{({\text{w}})}} = - \frac{{2{{A}_{6}}{{R}^{3}}}}{{3a{{\zeta }^{2}}}},\,\,\,\,f_{{\text{7}}}^{{({\text{w}})}} = - \frac{{8{{A}_{7}}{{R}^{3}}\left( {r - 1} \right)}}{{15{{a}^{2}}{{\zeta }^{3}}}},$(11)
${{F}_{{\text{w}}}} = \left( {F_{{\text{6}}}^{{\text{w}}}\left( {{{r}_{0}}} \right),\,\,r \leqslant {{r}_{0}},\,\,F_{{\text{6}}}^{{\text{w}}},\,\,r \leqslant \xi ,\,\,F_{{\text{7}}}^{{\text{w}}},\,\,r > \xi } \right),$Стационарные уравнения Стокса
и конвективной диффузии (9) решались численно методом конечных разностей с помощью схем, приведенных в [16, 19]. В уравнениях (12) $p = {{p{\text{*}}a} \mathord{\left/ {\vphantom {{p{\text{*}}a} {U\mu }}} \right. \kern-0em} {U\mu }}$ – безразмерное давление. На входной границе расчетной ячейки ставилось условие невозмущенной скорости $u = 1$ и однородной концентрации $n = 1.$ На поверхности волокна задавались условия прилипания или скольжения (в зависимости от величины ${\text{Kn}}$) и нулевой концентрации при $r = 1 + R.$ На боковых границах ячейки ставились условия симметрии для компонент скоростей и для концентрации, а на выходе из ячейки – условия отсутствия вязких напряжений и выравнивания концентрации.Коэффициент захвата частиц волокном определялся как интегральная плотность полного потока частиц на границу осаждения $\Gamma {\text{:}}$
где ${{j}_{{\text{N}}}}$ – нормальная компонента вектора плотности полного потока частиц (8) вдоль границы осаждения, $d\Gamma $ – элемент длины $\Gamma .$ Запишем (13) в полярных координатах:(14)
$\eta = \tilde {r}\int\limits_0^\pi {{{{\left( {2{\text{P}}{{{\text{e}}}^{{ - 1}}}{{\partial n} \mathord{\left/ {\vphantom {{\partial n} {\partial r - {{{v}}_{r}}n}}} \right. \kern-0em} {\partial r - {{{v}}_{r}}n}}} \right)}}_{{r = \tilde {r}}}}} d\theta {\text{,}}$Нисходящий поток
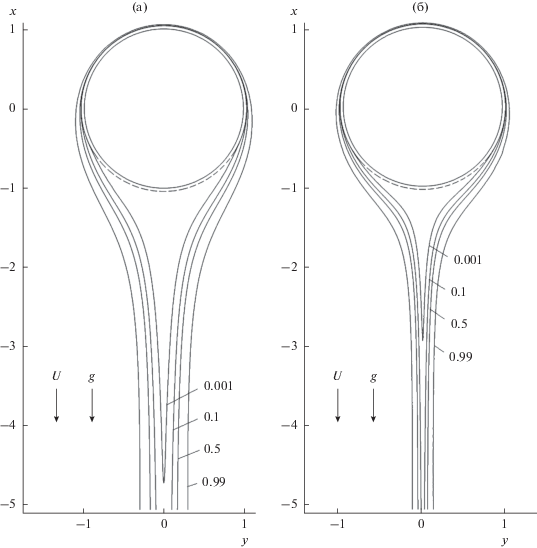
На рис. 2 приведены изолинии концентрации частиц у поверхности волокна в ряду волокон, обтекаемого нисходящим потоком (сверху вниз). Здесь $b = {a \mathord{\left/ {\vphantom {a h}} \right. \kern-0em} h}$ = 0.3 – параметр ряда, где $2h$ – расстояние между осями соседних волокон. Видно, что в случае крупных тяжелых частиц все частицы в верхней зоне волокна подходят вплотную к нему, а в области диффузионного следа за волокном образуется зона, свободная от частиц. При этом за счет дополнительного осаждения сверху гравитация увеличивает эффективность фильтра.
Рис. 2.
Изолинии безразмерной концентрации частиц при обтекании нисходящим потоком волокна в ряду волокон при $U$ = 0.3 (а) и 1 см/с (б); $b$ = 0.3, $\rho $ = 10.5 г/см3.
Были рассчитаны зависимости коэффициента захвата тяжелых частиц от их радиуса при фильтрации в нисходящем потоке в ячеечной модели. Они представлены на рис. 3, где для сравнения приведены кривые, рассчитанные без учета гравитации, которые монотонно убывают с ростом ${{r}_{{\text{p}}}}$ из-за уменьшения вклада диффузионного осаждения. Эти кривые не достигают минимума (максимума проскока), поскольку в данном примере при малой скорости потока рассмотрены толстые волокна. Из рисунков следует, что с учетом гравитации величина $\eta $ резко возрастает, почти на порядок, что нельзя не учитывать, т.к. величина $\eta $ входит в показатель экспоненты в формуле для эффективности фильтра (1). Прямое численное моделирование осаждения в ячейке и расчет по аддитивному приближению (6) дают довольно близкие значения $\eta $ и тот же характер зависимости $\eta $ от ${{r}_{{\text{p}}}}.$
Рис. 3.
Зависимости коэффициента захвата частиц в ячейке Кувабары из потока сверху вниз от их радиуса при $U$ = 0.3 cм/с: 1, 1 ' – расчет по (6) без учета гравитации, 2, 2 ' – прямое моделирование по (9), (14), 3, 3 ' – расчет по (6) с учетом гравитации; 1–3 – без учета сил Ван-дер-Ваальса, 1 '–3 ' – с учетом ван-дер-ваальсова взаимодействия при A7 = 10−18 эрг см; $\alpha $= 0.0707, $a$ = 15 мкм, $\rho $ = 10.5 г/см3.
Восходящий поток
Распределение концентрации при обтекании волокна потоком крупных частиц снизу вверх показано на рис. 4, где явно видно (как и на рис. 1), что перед обтекаемым волокном, а также в боковых зонах частицы отсутствуют. Зона нулевой концентрации тем заметнее, чем тяжелее частицы, но с ростом скорости потока толщина этой зоны убывает. При этом в области задней осевой линии небольшое осаждение все же имеет место – тяжелые частицы диффундируют в область диффузионного следа вдали от волокна и возвращаются к нему благодаря гравитации.
Рис. 4.
Изолинии безразмерной концентрации частиц при осаждении из восходящего потока в ряду волокон при $U$ = 0.3 (а) и 1 см/с (б); ${{r}_{{\text{p}}}}$ = 0.6 мкм, $\rho $ = 10.5 г/см3, $a$ = 15 мкм, $b$ = 0.3.
На рис. 5 приводится сравнение зависимостей коэффициента захвата частиц от их радиуса при фильтрации в восходящем потоке с учетом гравитации (кривые 2, 2 ' и 3, 3 ') и аналогичных зависимостей без учета гравитации (кривые 1, 1 '). Кривые 1, 1 ' и 3, 3 ', рассчитанные по формуле (6), резко различаются, откуда следует, что учет гравитации качественно изменяет характер осаждения – с ростом размера частиц коэффициент захвата резко уменьшается. Отметим, что учет действия сил Ван-дер-Ваальса (кривые 1 ' и 3 ') незначительно увеличил коэффициент захвата в данном примере (кривые 1 и 3), поскольку расчеты выполнены для толстых волокон. И совершенно другой вид имеют зависимости $\eta \left( {{{r}_{{\text{p}}}}} \right)$ (кривые 2, 2 '), полученные численным методом, когда учитывается осаждение частиц на обратной стороне волокна. На рис. 5 видно что, начиная с ${{r}_{{\text{p}}}}$ = 0.3 мкм, $\eta $ перестает уменьшаться и его значения выходят на плато. Убывание коэффициента захвата с ростом ${{r}_{{\text{p}}}}$ (кривые 1 и 3) происходит в результате уменьшения коэффициента диффузии и, следовательно, уменьшения диффузионного осаждения, причем рост осаждения за счет зацепления не успевает компенсировать это уменьшение, но его компенсирует гравитационное осаждение на обратной стороне волокна. Таким образом, при осаждении тяжелых частиц в условиях доминирующего влияния гравитации коэффициент захвата частиц из восходящего потока не становится исчезающе малым.
Рис. 5.
Зависимости коэффициента захвата частиц волокном в ячейке Кувабары из восходящего потока от их радиуса при = 0.3 см/с: 1, 1 ' – расчет по (6) без учета гравитации, 2, 2' – прямое моделирование по (14), 3, 3 ' – расчет по (6) с учетом гравитации; 1–3 – без учета сил Ван-дер-Ваальса, 1 '–3 ' – с учетом ван-дер-ваальсова взаимодействия при A7 = 10–18 эрг см; = 0.0707, = 15 мкм, = 10.5 г/см3.
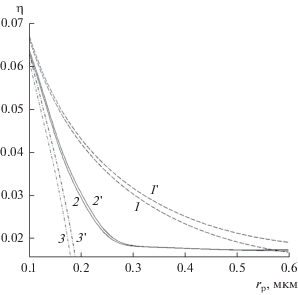
Для случая восходящего потока расчетные зависимости коэффициента захвата частиц разной плотности в ряду волокон от радиуса частиц приведены на рис. 6. При всех значениях плотности величина η мелких частиц падает с ростом ${{r}_{{\text{p}}}}$, так как уменьшается ηD. Кроме того, обратим внимание на то, что эффективность осаждения крупных и самых тяжелых частиц – такая же, как и частиц, на осаждение которых гравитация практически не влияет, поскольку имеет место осаждение на обратную сторону волокон по отношению к потоку. Таким образом, с ростом размера тяжелых частиц коэффициент захвата вначале убывает, а затем, когда начинается осаждение на обратной стороне волокна, он медленно растет в отличие от коэффициента захвата в ячейке, что связано с возможностью расчета в модели ряда волокон диффузии частиц в протяженном диффузионном следе за волокном. Ячеечная модель ограничена радиусом ячейки, а в модели ряда расчетная область может быть выбрана сколь угодно большой по направлению потока, что позволяет рассчитывать эволюцию диффузионного следа.
Горизонтальный поток
Влияние гравитации на осаждение частиц на волокно из горизонтального потока в зависимости от их плотности показано на рис. 7. Видно, что при малой скорости потока крупные тяжелые частицы не осаждаются на нижней стороне волокна. Под волокном образуется свободная от частиц зона. Также видно, что гравитация смещает частицы в гидродинамическом следе, из-за чего диффузионный след за волокном искривляется, становится несимметричным относительно потока и также смещается вниз. С ростом скорости потока этот эффект уменьшается и исчезает.
Рис. 7.
Изолинии безразмерной концентрации частиц при осаждении из горизонтального потока в ряду волокон при $U$ = 0.3 (а) и 1 см/с (б); ${{r}_{{\text{p}}}}$ = 0.6 мкм, $\rho $ = 10.5 г/см3, a = 15 мкм, $b$ = 0.3.
Как отмечалось выше, влияние гравитации увеличивает осаждение из горизонтального потока с ростом размера частиц при ${{r}_{{\text{p}}}}$ > 0.3 мкм. Начальное уменьшение коэффициента захвата частиц с ростом ${{r}_{{\text{p}}}}$ является следствием того, что падает диффузионная подвижность частиц, но затем начинает сказываться влияние гравитации, которое и ведет к росту осаждения частиц. И очевидно, что влияние гравитации проявляется сильнее с ростом плотности частиц (рис. 8). Если пренебречь вкладом гравитации (кривая 1), то осаждение будет идти только за счет эффектов диффузии и зацепления, и монотонное уменьшение коэффициента захвата будет наблюдаться вплоть до области “максимума проскока”.
Осаждение частиц в модельных фильтрах с трехмерным полем течения
Для экспериментального изучения влияния гравитации на осаждение частиц в условиях трехмерного течения, а именно, в области пересечения волокон в фильтре, мы выбрали сетки. При этом расчеты вели для модельных сеток, состоящих из двух повернутых на 90° соприкасающихся рядов волокон. Величины проскока частиц через сетки были найдены путем совместного численного решения уравнений Стокса и конвективной диффузии. На рис. 9 результаты расчетов для модельной сетки с трехмерным полем течения сравниваются с расчетами проскока частиц через два ряда волокон с двумерным полем течения в восходящем и нисходящем потоках. Сравнение показывает, что учет трехмерности течения не вносит существенных отличий: величины проскока через сетки практически равны произведению проскоков через два изолированных ряда волокон. Также отметим, что в случае восходящего потока кривые, описывающие проскок частиц через сетки, при малой скорости U имеют слабо выраженный максимум.
Рис. 9.
Расчетные зависимости коэффициента проскока тяжелых частиц через модельную сетку (1, 3) и через два ряда волокон (2, 4) от радиуса частиц: 1, 2 − восходящий поток, 3, 4 − нисходящий поток; $U$ = 0.3 см/с, $\rho $ = 10.5 г/см3, $a$ = 15 мкм, $b$ = 0.3.
Таким образом, из полученных данных следует, что осаждение на волокна фильтра тяжелых частиц из восходящего потока происходит и при малой скорости. Этот вывод, как будет показано ниже, подтверждается экспериментально.
3. ЭКСПЕРИМЕНТ
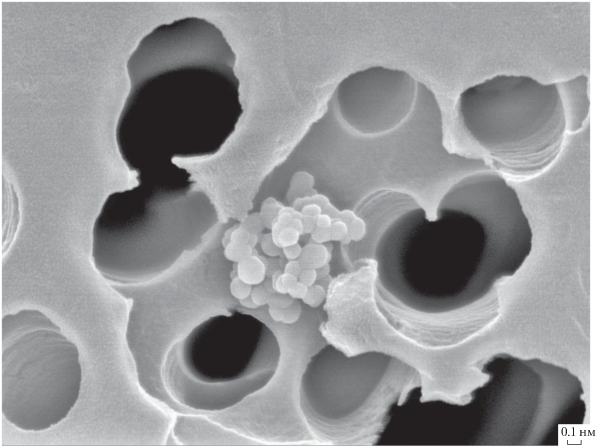
Для исследования осаждения в фильтре субмикронных частиц с высокой плотностью были использованы аэрозоли, которые получали диспергированием высокодисперсного порошка серебра в камере объемом 200 л. Образующиеся взвешенные частицы, состоящие из агрегированных наночастиц, имели несферическую форму. Крупные частицы быстро оседали, и в объеме оставались частицы субмикронного размера. На рис. 10 показаны частицы серебра, отобранные на аналитическом фильтре. Во взвешенном состоянии размер частиц определялся с помощью многоканального аэрозольного спектрометра. Для получения сферических частиц серебра поток аэрозоля пропускался через трубчатую печь при температуре 870°C с расходом 1 л/мин. На выходе получались сферические частицы (рис. 11).
На рис. 12 видно, что некоторые крупные частицы серебра не успевали полностью оплавиться. Они были достаточно компактными и состояли из мелких шариков. Бóльшая часть исходных и оплавленных частиц была заряжена. Заряженные частицы удалялись в конденсаторе, между пластинами которого создавалась разность потенциалов, причем было установлено, что наличие заряда почти не сказывалось на величине проскока частиц диаметром более 0.4 мкм.
Частицы субмикронного размера с трудом улавливаются в фильтрах и, как правило, являются в широком диапазоне скорости наиболее проникающими через волокнистые фильтры с разными параметрами. Поэтому для выяснения специфики фильтрации при малой скорости в качестве фильтров были использованы толстые слои металлических сеток, которые обеспечивали надежное измерение эффективности улавливания при ${n \mathord{\left/ {\vphantom {n {n{}_{0}}}} \right. \kern-0em} {n{}_{0}}}$ < 0.5.
Первая серия измерений проводилась с сетками из проволочек диаметром $2a$ = 30 мкм, расстояние между осями которых равно $2h$ = 100 мкм. Сетки площадью 10 см2 в количестве $N$ = 100, 200 и 300 штук помещались в одинаковые фильтродержатели. Особо отметим, что при выборе условий проведения экспериментов необходимо было исключить потери частиц в коммуникациях из-за малых расходов аэрозолей, пропускаемых через фильтр. С этой целью поток, подводимый к сеточному фильтру, разделялся на две части. Меньшая часть потока пропускалась через сетки, а бóльшая отфильтровывалась с помощью параллельного НЕРА-фильтра, и затем на выходе оба потока смешивались и поступали в спектрометр.
Схема установки показана на рис. 13, где видно, как переключаются потоки снизу вверх и сверху вниз, и что параллельно с фильтрами 4 и 5 находился фильтр-держатель 6 с одной сеткой (измеряемая концентрация частиц на выходе соответствовала концентрации до фильтра ${{n}_{0}}$). Для измерения осаждения частиц из горизонтального потока фильтры поворачивали.
Рис. 13.
Схема установки для измерения осаждения частиц: 1 – генератор частиц, 2 – камера с аэрозолем, 3 – краны для переключения направления потока, 4 – стекловолокнистый фильтр, 5 – сеточный фильтр, 6 – фильтр-держатель с одной сеткой, 7 – дифференциальный манометр, 8 – запорные краны, 9 – расходомер, 10 – “абсолютный” фильтр, 11 – спектрометр (счетчик) аэрозолей.
Вторая серия измерений при малой скорости проводилась с тонкими стекловолокнистыми материалами. Изменение скорости достигалось за счет увеличения площади фильтра. Подходящие значения проскока подбиралось за счет числа слоев. Для измерения размеров и концентрации частиц использовался фотоэлектрический счетчик 11.
4. РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
В опытах с одновременным измерением проскока через три фильтра, состоящих из 100, 200 и 300 сеток, при скорости 1 см/с было показано, что при направлении потока снизу вверх зависимость проскока частиц от числа сеток имеет экспоненциальный характер, в том числе, в области размеров частиц, для которых начинает заметно проявляться влияние гравитации. Совпадение значений коэффициента захвата наблюдалось для частиц всех размеров.
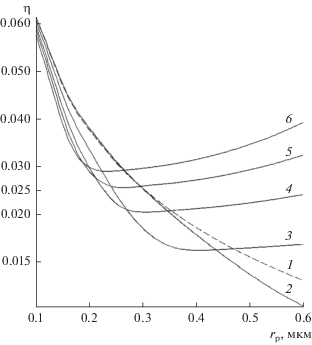
Измеренные значения проскока для фильтра, состоящего из 100 сеток, представлены на рис. 14. В этих опытах скорость седиментации крупных частиц с ${{r}_{{\text{p}}}}$ = 0.5 мкм и ρ = 10 г/см3 (с учетом поправки Каннингема) составляла 0.035 см/с. Здесь точками показаны результаты измерений проскока при двух значениях скорости, $U$ = 0.3 см/с (а) и $U$ = 1 см/с (б), а сплошными кривыми – результаты расчета проскока по формуле (1), которая для сеток и рядов имеет вид: ${n \mathord{\left/ {\vphantom {n {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}} = \exp \left( { - 2aL\eta } \right),$ где $L = {N \mathord{\left/ {\vphantom {N {2h}}} \right. \kern-0em} {2h}}$ – длина волокон, приходящаяся на единицу площади фильтра, $N$ − число сеток или рядов параллельных волокон, $2h$ – расстояние между волокнами в ряду. Кривые 1, 3 относятся к сеткам ($N$ = 100), кривые 2, 4 – к 200 отдельным рядам волокон (эквивалент 100 сеток). Коэффициенты захвата η для единицы длины волокна были найдены прямым численным моделированием осаждения частиц на сетке, состоящей из двух скрещенных рядов волокон, и в изолированном ряду параллельных волокон. Видно, что влияние гравитационного осаждения начинает проявляться для частиц уже с ${{r}_{{\text{p}}}}$ > 0.1 мкм, и при ${{r}_{{\text{p}}}}$ > > 0.2 мкм проскок частиц из восходящего потока становится почти на порядок больше, чем из нисходящего. Но только при ${{r}_{{\text{p}}}}$ > 0.3 мкм, когда гравитационный механизм осаждения становится основным, проскок в восходящем потоке больше не растет, а остается почти постоянным. То же самое наблюдается и в случае горизонтального потока (рис. 15).
Рис. 14.
Зависимости проскока частиц от их радиуса для 100 плетеных сеток (1, 3, 5, 6) и 200 рядов параллельных волокон (2, 4) при $U$ = 0.3 (a) и 1 см/с (б): 1–4 – расчет, 5, 6 – эксперимент; 1, 2, 5 – восходящий поток, 3, 4, 6 – нисходящий поток; $\rho $ = 10.5 г/см3, $b$ = 0.3.
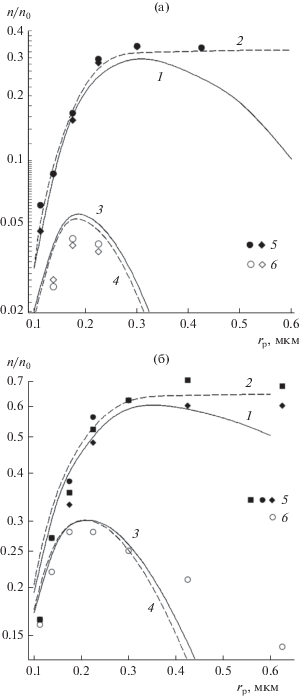
Рис. 15.
Зависимости коэффициента проскока частиц через 100 плетеных сеток от радиуса частиц в горизонтальном потоке при $U$ = 0.3 (1, 3) и 1 см/с (2, 4): 1, 2 – расчет, 3, 4 – эксперимент; $\rho $ = 10.5 г/см3, $b$ = 0.3.
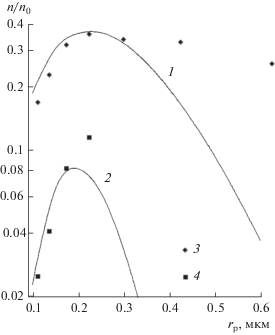
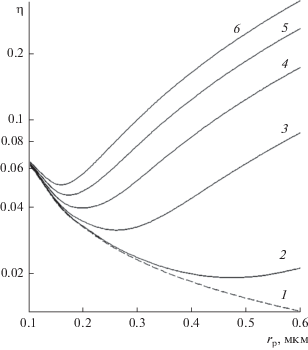
Для исследования фильтрации при малой скорости реальными фильтрами были выбраны тонкие стекловолокнистые материалы (стекловуаль) со средним диаметром волокон, равным $\left\langle a \right\rangle $ = = 2.74 мкм, ${{\left\langle {{{a}^{2}}} \right\rangle }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ = 3.2 мкм, ${{\alpha }_{0}}H$ = 1.72 × 10−3, ${{\alpha }_{0}}$ = 0.03 [20]. На рис. 16 приведены результаты измерений эффективности улавливания серебряных частиц в тонковолокнистых фильтрах при скорости $U$ = 0.3 см/с. Для достижения заметного осаждения использовались фильтры, состоящие из 5 и 10 слоев волокон. Числа Стокса были малы, ${\text{Stk}}$ < 0.1, поэтому даже для самых крупных частиц инерционное осаждение исключалось.
Рис. 16.
Коэффициенты проскока частиц через стекловолокнистый фильтр из 5 (а) и 10 слоев (б) в восходящем (1, 4), горизонтальном (2, 5) и нисходящем (3, 6) потоках в зависимости от радиуса частиц при $U$ = 0.3 см/с. Параметры фильтра приведены в тексте.
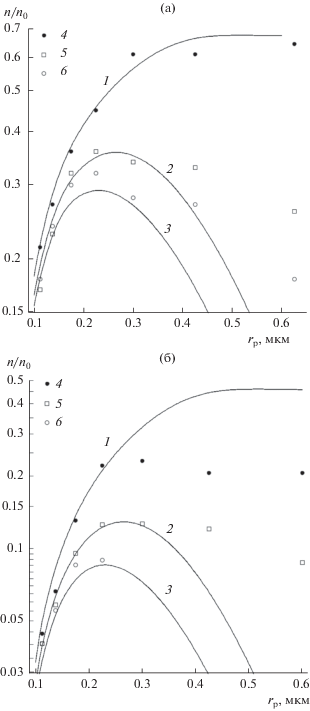
Поскольку структура стекловуали никак не определена, невозможен прямой численный расчет коэффициента захвата и проскока частиц для этого фильтра. Поэтому для сравнения с экспериментом мы рассчитали коэффициент захвата для изолированного ряда волокон с теми же средним радиусом волокон и параметром $b = 2{{\left( {{\alpha \mathord{\left/ {\vphantom {\alpha \pi }} \right. \kern-0em} \pi }} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$ соответствующимплотностиупаковки вуали. Экспериментальные значения коэффициента захвата определили по формуле для модельного веерного фильтра также для среднего радиуса $\left\langle a \right\rangle $ по формуле (6), где $l = {\alpha \mathord{\left/ {\vphantom {\alpha {\pi \left\langle {{{a}^{2}}} \right\rangle }}} \right. \kern-0em} {\pi \left\langle {{{a}^{2}}} \right\rangle }},$ и воспользовались тем экспериментальным фактом, что измеренный коэффициент захвата меньше расчетного для веерной модели во столько раз, во сколько измеренная средняя сила сопротивления $F$ меньше, чем сила ${{F}^{{\text{f}}}}$ для веерной модели [5]. Из измерений перепада давления рассчитали $F$ по формуле (3), а по формуле (5) при $\alpha = {{{{\alpha }_{0}}} \mathord{\left/ {\vphantom {{{{\alpha }_{0}}} {\left( {{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} \right)}}} \right. \kern-0em} {\left( {{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} \right)}}$ нашли ${{F}^{{\text{f}}}}$ [5]. Перепад давления в фильтре, состоящем из 5 и 10 слоев, измерялся в зависимости от скорости в диапазоне ее значений от 0.3 до 100 см/с. Поскольку величины $\Delta p{\kern 1pt} *$ были малы, то сжатия фильтра не наблюдалось, о чем свидетельствовала строгая линейность зависимости $\Delta p{\text{*}}\left( U \right)$ во всем диапазоне скорости. Рассчитанная из $\Delta p{\text{*}}\left( U \right)$ по (4) средняя сила сопротивления стекловолокна равна ${{F}^{{\text{f}}}}$ = 5.0, что в 1.7 меньше, чем в эталонном фильтре. Из данных, приведенных на рис. 16, следует, что значения проскока в восходящих потоках значительно больше, чем в нисходящих. При ${{r}_{{\text{p}}}}$ < 0.3 мкм экспериментальные результаты удовлетворительно согласуются с расчетом для 5 и 10 слоев, что свидетельствует о существовании экспоненциальной зависимости проскока частиц от толщины фильтра даже в области существенного влияния гравитации, при этом для частиц большего размера теория переоценивает реальную эффективность фильтра. И важно отметить, что в случае восходящего потока экспериментальные данные не превышают расчетных – эффективность фильтров не стремится к нулю с ростом ${{r}_{{\text{p}}}}$, как это следует из оценок по (6).
5. ЗАКЛЮЧЕНИЕ
Теоретически и экспериментально изучено осаждение частиц в волокнистом фильтре с учетом влияния гравитации. На основе прямого численного решения уравнений Стокса и уравнения конвективной диффузии с учетом конечного размера частиц рассчитаны коэффициенты захвата в модельных фильтрах с двух- и трехмерной структурой в зависимости от параметров фильтров, размера и плотности частиц и условий фильтрации.
Результаты расчетов подтверждаются проведенными экспериментами по осаждению субмикронных сферических серебряных частиц из восходящих и нисходящих потоков в сетках и в фильтрах при малой скорости течения газа. Показано существенное влияние гравитации на осаждение субмикронных частиц с высокой плотностью при малой скорости потока. Особенно заметно ее влияние при осаждении таких частиц из восходящего потока в фильтрах. В этом случае эффективность фильтрации резко падает с ростом размера частиц; при этом она не стремится к нулю, как это следует из оценок по формуле (6). Показано, что хотя средняя скорость потока в фильтре больше скорости седиментации частиц, но при обтекании волокна потоком частицы падают на волокно сверху, так как над волокном, особенно вблизи его поверхности, в области гидродинамического следа скорость восходящего потока меньше скорости седиментации. Это – принципиальный результат, указывающий на то, что влияние гравитации в восходящем потоке не уменьшает эффективность фильтра до нуля. В этом случае эффективность фильтрации много меньше, чем при горизонтальном направлении потока и, тем более, при нисходящем потоке. Этот вывод относится к фильтрации при малых скоростях потока. При обычной скорости, порядка нескольких см/с, влияние гравитации даже для тяжелых частиц сказывается менее заметно. Это следует учитывать при создании фильтрующих систем для очистки воздуха с очень малым расходом и не устанавливать фильтр в восходящем потоке, в котором осаждение частиц мало. И, наоборот, целесообразно, использовать фильтрующие системы с потоком, направленным сверху вниз, когда гравитационное осаждение увеличивает эффективность фильтра.
Полученные результаты соответствуют начальной стадии работы фильтра. Очевидно, что процесс забивки фильтров тяжелыми частицами будет заметно отличаться от случая, когда гравитация не влияет на осаждение. Заранее неизвестно, как будет изменяться эффективность фильтра по мере забивки, поскольку рост осадка на волокнах приведет к росту скорости потока в зазорах между волокнами. Вклад гравитационного механизма осаждения частиц усложнит задачу расчета ресурса фильтра. Эти вопросы требуют специального рассмотрения.
Список литературы
Lippmann M. // Aerosols Handbook, Measurement, Dosimetry, and Health Effect. Ed. by Ruser L.S., Harley N.H. Boca Raton: CRC Press, 2013, P. 357.
Dyment J. // Proc. Int. Colloq. Radioactive Pollution of Gaseous Media, CEN, Saslay, 1963. P. 395.
Fuchs N.A. Mechanics of Aerosols. Oxford: Pergamon Press, 1964.
Thomas J.W., Rimberg D., Miller T.J. // J. Aerosol Sci. 1971. V. 2. P. 31.
Kirsch A.A., Stechkina I.B. // Fundamentals of Aerosol Science. Ed. by Shaw D.T. N.Y.: Wiley-Interscience, 1978. P. 165.
Kuwabara S. // J. Phys. Soc. Jpn. 1959. V. 14. P. 527.
Кирш В.А. // Коллоид. журн. 2000. Т. 62. С. 790.
Кирш В.А. // Коллоид. журн. 2004. Т. 66. С. 497.
Pich J. // Filtration: Principles and Practices, Ed. by Matteson M. and Orr C. N.Y.: Marcel Dekker, 1987. P. 1.
Davies C.N. Air Filtration. N.Y.: Academic Press, 1973.
Brown R.C. Air Filtration. Oxford: Pergamon Press, 1993.
Kanaoka C. // KONA Powder and Particle J. 2019. № 36. P. 88.
Araujo A.D., Andrade J.S. Jr., Herrmann H.J. // Phys. Rev. Let. 2006. V. 97. Article 138 001.
Кирш В.А. // Теор. основы хим. технологии. 2005. Т. 39. С. 50.
Кирш В.А. // Коллоид. журн. 2005. Т. 67. С. 352.
Берковский Б.М., Полевиков В.К. // Инж.-физ. журн. 1973. Т. 24. С. 842.
Hamaker H.C. // Physica. 1937. V. 4. P. 1058.
Bouwkamp C.J. // Physica. 1947. V. 13. P. 501.
Берковский Б.М., Ноготов Е.Ф. Разностные методы исследования задач теплообмена. Минск: Наука и Техника, 1976.
Черняков А.Л., Кирш А.А. // Коллоид. журн. 2014. Т. 76. С. 228.
Дополнительные материалы отсутствуют.
Инструменты
Коллоидный журнал