Коллоидный журнал, 2021, T. 83, № 4, стр. 412-422
О динамических коэффициентах вязкости и релаксационных процессах в магнитных жидкостях
А. К. Зарипов *
Таджикский национальный университет
734025 Душанбе, проспект Рудаки, 17, Таджикистан
* E-mail: afzal.z@mail.ru
Поступила в редакцию 03.12.2020
После доработки 10.01.2021
Принята к публикации 25.01.2021
Аннотация
Исследована частотная дисперсия динамических коэффициентов вязкости, полученных как на основе уравнения Смолуховского, описавшего диффузионный механизм релаксации, так и на основе аппроксимации Бхатнагара–Гросса–Крука, приводящей к экспоненциальному затуханию тензора напряжения магнитных жидкостей. В первом случае функция Грина, содержащаяся в интегральных частях коэффициентов переноса, является медленно затухающей функцией, изменяющейся по закону ${{t}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}},$ который обнаружен во многих компьютерных экспериментах. В этом случае область частотной дисперсии коэффициентов вязкости как следствие степенного затухания релаксирующих потоков, является очень широкой. Во втором случае область частотной дисперсии коэффициентов вязкости, как следствие экспоненциального затухания тензора напряжения, является узкой и совпадает с экспериментальными результатами.
ВВЕДЕНИЕ
Магнитные жидкости, обладая уникальными свойствами, открывают широкие возможности их технического применения и поэтому привлекают все большее внимание исследователей. Научные рекомендации по техническому применению магнитных жидкостей зависят от уровня проведенных экспериментальных и теоретических исследований их физико-химических характеристик. Теоретические исследования магнитных жидкостей базируются на существующих теориях жидкостей и ведутся в разных направлениях с привлечением феноменологических теорий, строгих статистических методов, численных методов и модельных теорий. Жидкости, занимающее промежуточное положение между твердыми и газообразными веществами, имеют специфические свойства, связанные с их сложной структурой и силами, действующими между молекулами. В силу сложной структуры жидкостей законченной количественной теории жидкого состояния до настоящего времени не существует.
Одним из плодотворных подходов к исследованию жидкостей является статистическая теория, к которой можно отнести временны́е корреляционные функции Ван-Хова, методы Энскога, проекционных операторов Мори, неравновесных статистических операторов Зубарева, молекулярно-кинетической теории и др. Хотя во всех этих методах очень ясно и красиво определяются кинетические коэффициенты, поведение корреляционных функций в них при достаточно больших временах отличается друг от друга, и это соответственно приводит к различным результатам по частотной дисперсии кинетических коэффициентов и акустических параметров.
Ранее проведенные исследования на основе простых моделей, таких как броуновское движение, теория марковских случайных процессов и уравнение Больцмана, привели специалистов к убеждению, что автокорреляционные функции со временем затухают экспоненциально. Однако вычисление корреляционных функций, содержащих функцию Грина и учитывающих корреляции положений и скоростей, показало, что эти функции могут изменяться не экспоненциально, а по степенному закону.
Впервые в [1] на основе машинного эксперимента методом молекулярной динамики было показано, что автокорреляционная функция скоростей в течение длительного времени, не распадаясь экспоненциально, изменяется по закону ${{t}^{{{{ - d} \mathord{\left/ {\vphantom {{ - d} 2}} \right. \kern-0em} 2}}}},$ где $d$ – размерность системы. Эта работа привлекала внимание многих специалистов, и несколько позже такой же характер затухания автокорреляционных функций был обнаружен в теоретических работах [2–6]. Особое внимание этому вопросу уделили Резибуя с коллегами [7, 8]. Они, как на основе феноменологической теории с применением метода Ландау–Плачека, так и на основе кинетической теории, подробно исследовав поведение временны́х корреляционных функций, показали, что медленное затухание подынтегральных функций Грина–Кубо по степенному закону обусловлено коллективным гидродинамическим эффектом и распространением флуктуации гидродинамических переменных на большие расстояния.
Фишер [6], исследуя происхождение долговременных хвостов корреляционных функций при описании процессов переноса, исходил из того, что скорость теплового движения молекул можно представить в виде суммы двух составляющих:
где ${{\upsilon }_{{\text{c}}}}(t)$ представляет коллективное перемещение ближайших молекул, а $\upsilon {\kern 1pt} {\text{'}}(t)$ – скорость движения выбранной молекулы относительно ее окружения. Принимая эти составляющие как статистически независимые, движение выбранной молекулы он рассматривал как совместное со своим окружением в составе “жидкой частицы”, впоследствии называемой лагранжевой частицей. Далее он предполагал, что временнáя эволюция ${{\upsilon }_{{\text{c}}}}(t)$ – более медленная и автокорреляционную функцию скорости аппроксимировал для частицы Лагранжа. Для расчета автокорреляционной функции, принимая лагранжевую теорию тепловых гидродинамических флуктуаций, Фишер получил результаты, которые полностью согласовывались как с результатами феноменологических подходов [2–4], так и с расчетами, проведенными на основе молекулярно-кинетической теории [5, 7, 8]. Дальнейшее развитие метода, предложенного в [6], можно видеть в работах [9–11], где построена последовательная теория тепловых гидродинамических флуктуаций Лагранжа и с применением метода молекулярной динамики детально анализируется автокорреляционная функция скорости частицы Лагранжа.Необходимо отметить, что, хотя долговременные хвосты автокорреляционных функций подробно исследованы во многих теоретических работах, до настоящего времени физические эксперименты по доказательству их существования практически отсутствуют. Однако методы компьютерного моделирования имеют широкие возможности наглядно показать медленное затухание автокорреляционных функций, содержащихся в выражениях для коэффициентов переноса. Как известно, автокорреляционная функция скоростей позволяет определить усредненные характеристики движения микрочастиц, и исследование этой функции методом молекулярной динамики дает возможность выявить основные закономерности коллективных движений частиц в жидкости.
В обзоре [12], который посвящен методу молекулярной динамики и его применению в статистической физике, подробно проанализировано долговременное поведение временны́х корреляционных функций скорости, автокорреляционных функций сила–сила, плотность–плотность и показано, что их распад всегда подчиняется закону ${{t}^{{{{ - d} \mathord{\left/ {\vphantom {{ - d} 2}} \right. \kern-0em} 2}}}}.$ Там же отмечается, что справедливость результатов, полученных в [1] для трехмерной системы твердых шариков, содержащей 500 частиц, при установлении асимптотического закона ${{t}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}}$ ставится под сомнение из-за слишком малого числа частиц. Однако исследования, проведенные для системы, содержащей 4000 частиц [13], подтвердили справедливость асимптотического закона ${{t}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}},$ обнаруженного в [1]. Работы по исследованию свойств простых жидкостей для систем из 32 000 и 10 976 частиц [14], для моделей воды из 10 000 и 50 000 молекул [11], а также дисперсных систем с 8000 частицами и различным соотношением масс наночастиц и молекул несущей среды [15, 16] показывают, что закон ${{t}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}},$ проявляющийся при исследовании коллективных релаксационных процессов, является всеобщим и его можно наблюдать во всех жидкостях.
Нами ранее [17–20] на основе метода молекулярно-кинетической теории были исследованы вязкоупругие и акустические свойства магнитных жидкостей с учетом различных релаксационных процессов. В [17] на основе кинетических уравнений, учитывающих вклады пространственных корреляций плотности и корреляции скоростей, получены микроскопические уравнения обобщенной гидродинамики, учитывающие различные релаксационные процессы. Также получено уравнение Смолуховского, описывающее поведение неравновесной бинарной плотности ${{n}_{2}}({{{\mathbf{q}}}_{1}},{{{\mathbf{q}}}_{2}},t)$ в конфигурационном пространстве и найдено его общее решение. Показано, что фундаментальным решением уравнения Смолуховского является функция Грина $G(r,{{r}_{1}},t - {{t}_{1}}),$ асимптотика которой при больших временах совпадает с асимптотиками автокорреляционных функций, т.е. имеет место закон ${{t}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}}.$
В этой и других наших работах, как следствие медленного затухания функции Грина, область частотной дисперсии коэффициентов переноса, модулей упругости и акустических параметров всегда являлась широкой и составляла пять декад. В работе [21], где магнитная жидкость рассматривается как многокомпонентная система, асимптотика функций Грина также подчиняется закону ${{t}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}}.$
Хотя многие теоретические модели показывают существование широкого спектра частотной дисперсии для многих жидкостей и суспензий, в экспериментальных работах область частотной дисперсии коэффициентов переноса и акустических параметров простых жидкостей [22], а также ферроколлоидов [23] не превышает 1–2 декад. Согласно [22], для некоторых жидкостей с очень большой вязкостью, таких как канифоль и полиметилметакрилат, в области затвердевания удалось наблюдать широкий релаксационный спектр, а для некоторых вязких масел область частотной дисперсии составляла до пяти декад.
Целью настоящей работы является исследование динамических коэффициентов вязкости в модели двухкомпонентной магнитной жидкости, когда релаксирующие потоки затухают как по степенному закону, так и экспоненциально.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ И УРАВНЕНИЯ
Сначала приведем некоторые результаты из работы [21]. В ней для двухкомпонентной магнитной жидкости, состоящей из ферритной (индекс $f$) и молекулярной (индекс $s$) подсистем, получены кинетические уравнения для одночастичной, ${{f}_{{1i}}}({{{\mathbf{q}}}_{1}},{{{\mathbf{p}}}_{1}},t),$ и двухчастичной, ${{f}_{{2i}}}({{{\mathbf{q}}}_{1}},{{{\mathbf{q}}}_{2}},{{{\mathbf{p}}}_{1}},{{{\mathbf{p}}}_{2}},t),$ функций распределения, описывающие необратимые процессы. На основе этих уравнений получена система уравнений обобщенной гидродинамики, в которые входят тензоры напряжения [21]
(1)
$\begin{gathered} \sigma _{i}^{{\alpha \beta }}\left( {{{{\mathbf{q}}}_{1}},t} \right) = - K_{i}^{{\alpha \beta }}({{{\mathbf{q}}}_{1}},t) + \\ + \,\,\frac{1}{2}\int {\frac{{\partial {{\Phi }_{i}}(r)}}{{\partial r}}\frac{{{{r}^{\alpha }}{{r}^{\beta }}}}{r}{{n}_{{2i}}}({{{\mathbf{q}}}_{1}},{\mathbf{r}},t)d{\mathbf{r}}} , \\ \end{gathered} $Как видно, тензоры напряжения $\sigma _{i}^{{\alpha \beta }}\left( {{{{\mathbf{q}}}_{1}},t} \right)$ состоят из кинетической $K_{i}^{{\alpha \beta }}\left( {{{{\mathbf{q}}}_{1}},t} \right)$ = ${{P}_{{ki}}}\left( {{{{\mathbf{q}}}_{1}},t} \right){{\delta }^{{\alpha \beta }}} + $ $ + \,\,k_{i}^{{\alpha \beta }}\left( {{{{\mathbf{q}}}_{1}},t} \right)$ и потенциальной частей. Потенциальная часть (1) определяется функцией неравновесной бинарной плотности ${{n}_{{2i}}}({{{\mathbf{q}}}_{1}},{\mathbf{r}},t),$ описывающей процесс перестройки структуры жидкости. Впервые для функции ${{n}_{2}}({{{\mathbf{q}}}_{1}},{\mathbf{r}},t)$ Кирквудом [24] было получено уравнение Смолуховского. Решение этого уравнения описывает пространственно-временнóе изменение структуры жидкости и, следовательно, процесс структурной релаксации. Однако общее решение этого уравнения Кирквудом с последователями не было найдено, и поэтому они не рассматривали релаксационные процессы.
На основе кинетических уравнений в [17] было получено уравнение Смолуховского для бинарной плотности частиц магнитных жидкостей, которое для i-ой подсистемы записывается в виде
(2)
$\frac{{\partial n_{{2i}}^{'}}}{{\partial t}} + {{\omega }_{{0i}}}{{\hat {L}}_{i}}n_{{2i}}^{'}\left( {{{{\mathbf{q}}}_{1}},{\mathbf{r}},t} \right) = {{R}_{i}}\left( {{{{\mathbf{q}}}_{1}},{\mathbf{r}},t} \right),$(3)
$n_{{2i}}^{'}({{{\mathbf{q}}}_{1}},{\mathbf{r}},t) = \int\limits_0^t {d{{t}_{1}}} \int\limits_{ - \infty }^\infty {{{G}_{i}}(r,{{r}_{1}},t - {{t}_{1}}){{R}_{i}}({{{\mathbf{q}}}_{1}},{{{\mathbf{r}}}_{1}},{{t}_{1}})d{{{\mathbf{r}}}_{1}}} ,$(4)
$\begin{gathered} {{G}_{i}}\left( {r,{{r}_{1}},t - {{t}_{1}}} \right) = 2{{\left( {2\pi } \right)}^{{ - 3}}}{{\left( {r{{r}_{1}}} \right)}^{{ - 1}}}{{\left( {\frac{\pi }{{\omega \left( {t - {{t}_{1}}} \right)}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} \times \\ \times \,\,\left\{ {\exp \left[ { - \frac{{{{{\left( {r - {{r}_{1}}} \right)}}^{2}}}}{{4\omega \left( {t - {{t}_{1}}} \right)}}} \right] - \exp \left[ { - \frac{{{{{\left( {r + {{r}_{1}}} \right)}}^{2}}}}{{4\omega \left( {t - {{t}_{1}}} \right)}}} \right]} \right\}, \\ {{R}_{i}}\left( {{{{\mathbf{q}}}_{1}},{\mathbf{r}},t} \right) = - {\kern 1pt} \left[ {{{\varphi }_{i}}\left( r \right) + \frac{{n_{i}^{2}{{\mu }_{0}}}}{{9{{\beta }_{i}}}}\left( {{\mathbf{m}}\nabla } \right){{{\left( {\frac{{\partial H}}{{\partial \upsilon }}} \right)}}_{{{{n}_{i}},T}}}{\kern 1pt} r\left( {\frac{{\partial {{g}_{i}}(r)}}{{\partial r}}} \right)} \right] \times \\ \times \,\,{\text{div}}{\mathbf{\dot {u}}} - \varphi _{i}^{{\alpha \beta }}\left( r \right)\left[ {1 + \frac{{{{\mu }_{0}}}}{{3{{\beta }_{i}}}}\left( {{\mathbf{m}}\nabla } \right){{{\left( {\frac{{\partial H}}{{\partial \upsilon }}} \right)}}_{{{{n}_{i}},T}}}} \right]\left\{ {\frac{{\partial {{{\dot {u}}}^{\alpha }}}}{{\partial q_{1}^{\beta }}}} \right\}, \\ {{\varphi }_{i}}\left( r \right) = 2n_{i}^{2}{{g}_{i}}\left\{ {1 + \frac{1}{6}\frac{{\partial \ln {{g}_{i}}(r)}}{{\partial \ln r}} - } \right. \\ \left. { - \,\,\frac{1}{2}\left[ {{{n}_{i}}{{{\left( {\frac{{\partial \ln {{g}_{i}}(r)}}{{\partial {{n}_{i}}}}} \right)}}_{T}} + {{\gamma }_{i}}T{{{\left( {\frac{{\partial \ln {{g}_{i}}(r)}}{{\partial T}}} \right)}}_{{{{n}_{i}}}}}} \right]} \right\}, \\ \varphi _{i}^{{\alpha \beta }}\left( r \right) = 2n_{i}^{2}\frac{{\left( {{{r}^{\alpha }}{{r}^{\beta }} - \frac{1}{3}{{r}^{2}}{{\delta }^{{\alpha \beta }}}} \right)}}{r}\frac{{\partial {{g}_{i}}}}{{\partial r}}, \\ {{{\hat {L}}}_{i}} = - \frac{\partial }{{\partial {{r}^{\alpha }}}}\left[ {\frac{\partial }{{\partial {{r}^{\alpha }}}} - \frac{\partial }{{\partial {{r}^{\alpha }}}}\ln {{g}_{i}}\left( r \right)} \right], \\ \end{gathered} $Подставляя (3) в (1) и совершая фурье-преобразование по времени, после его сравнения с фурье-образом макроскопического тензора вязких напряжений [25]
(5)
$\begin{gathered} {{\sigma }^{{\alpha \beta }}}\left( {{{{\mathbf{q}}}_{1}},t} \right) = K{\text{div}}{\mathbf{u}}{{\delta }^{{\alpha \beta }}} + {{{{\eta }}}_{{\text{v}}}}{\text{div}}{\mathbf{\dot {u}}}{{\delta }^{{\alpha \beta }}} + \\ + \,2\mu \left( {{{u}^{{\alpha \beta }}} - \frac{1}{3}{\text{div}}{\mathbf{u}}{{\delta }^{{\alpha \beta }}}} \right) + 2{{\eta }_{s}}\left( {{{{\dot {u}}}^{{\alpha \beta }}} - \frac{1}{3}{\text{div}}{\mathbf{\dot {u}}}{{\delta }^{{\alpha \beta }}}} \right), \\ \end{gathered} $(6)
$\begin{gathered} {{\eta }_{{\text{s}}}}\left( \omega \right) = \sum\limits_{i = f,s} {\frac{{{{n}_{i}}kT{{\tau }_{{1i}}}}}{{1 + {{{(\omega {{\tau }_{{1i}}})}}^{2}}}} + } \sum\limits_{i = f,s} {\frac{{n_{i}^{2}\sigma _{i}^{3}}}{{120\pi }}} \int\limits_0^\infty {\frac{{\partial {{\Phi }_{i}}}}{{\partial r}}} \times \\ \times \,\,\int\limits_0^\infty {{{G}_{i}}(r,{{r}_{1}},\omega )\frac{{\partial {{g}_{i}}({{r}_{1}})}}{{\partial {{r}_{1}}}}d{{{\mathbf{r}}}_{1}}d{\mathbf{r}}} + \frac{{n_{f}^{2}\sigma _{f}^{3}}}{{360\pi }} \times \\ \times \,\,\int\limits_0^\infty {\frac{{\partial {{\Phi }_{f}}}}{{\partial r}}} \int\limits_0^\infty {{{G}_{f}}(r,{{r}_{1}},\omega )\frac{{{{\mu }_{0}}}}{{{{\beta }_{f}}}}\left( {{\mathbf{m}}\nabla } \right)\frac{{\partial H}}{{\partial \upsilon }}\frac{{\partial {{g}_{f}}({{r}_{1}})}}{{\partial {{r}_{1}}}}d{{{\mathbf{r}}}_{1}}d{\mathbf{r}}} , \\ \end{gathered} $(7)
$\begin{gathered} {{\eta }_{{\text{v}}}}\left( \omega \right) = \sum\limits_{i = f,s} {\frac{{n_{i}^{2}\sigma _{i}^{3}}}{{24\pi }}} \int\limits_0^\infty {\frac{{\partial {{\Phi }_{i}}}}{{\partial r}}} \int\limits_0^\infty {{{G}_{i}}(r,{{r}_{1}},\omega ){{\varphi }_{i}}({{r}_{1}})r_{1}^{{ - 1}}d{{{\mathbf{r}}}_{1}}d{\mathbf{r}}} + \\ + \,\,\frac{{n_{f}^{2}\sigma _{f}^{3}}}{{216\pi }}\int\limits_0^\infty {\frac{{\partial {{\Phi }_{f}}}}{{\partial r}}} \int\limits_0^\infty {{{G}_{f}}(r,{{r}_{1}},\omega )\frac{{{{\mu }_{0}}}}{{{{\beta }_{f}}}}\left( {{\mathbf{m}}\nabla } \right)\frac{{\partial H}}{{\partial \upsilon }}\frac{{\partial {{g}_{f}}({{r}_{1}})}}{{\partial {{r}_{1}}}}} d{{{\mathbf{r}}}_{1}}d{\mathbf{r}}, \\ \end{gathered} $Из (4) следует, что при $(t - {{t}_{1}}) \to \infty $ функция ${{G}_{i}}\left( {r,{{r}_{1}},t - {{t}_{1}}} \right)$ имеет асимптотику
(8)
$\begin{gathered} {{\eta }_{s}}(\omega ) = {{\eta }_{s}}(0) + \sum\limits_{i = f,s} {{{{\left( {{{\omega {{\tau }_{{0i}}}} \mathord{\left/ {\vphantom {{\omega {{\tau }_{{0i}}}} 2}} \right. \kern-0em} 2}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} {{A}_{{si}}} + {{\left( {{{\omega {{\tau }_{{0f}}}} \mathord{\left/ {\vphantom {{\omega {{\tau }_{{0f}}}} 2}} \right. \kern-0em} 2}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\frac{{{{A}_{f}}}}{5}, \\ {{\eta }_{{\text{v}}}}(\omega ) = {{\eta }_{{\text{v}}}}(0) + \sum\limits_{i = f,s} {{{{\left( {{{\omega {{\tau }_{{0i}}}} \mathord{\left/ {\vphantom {{\omega {{\tau }_{{0i}}}} 2}} \right. \kern-0em} 2}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} {{A}_{{{\text{v}}i}}} + {{\left( {{{\omega {{\tau }_{{0f}}}} \mathord{\left/ {\vphantom {{\omega {{\tau }_{{0f}}}} 2}} \right. \kern-0em} 2}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\frac{{{{A}_{f}}}}{3}, \\ \end{gathered} $Видно, что в гидродинамическом режиме коэффициенты вязкости имеют асимптотики, пропорциональные ${{(\omega {{\tau }_{0}})}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$ что совпадает с низкочастотными асимптотиками [26–28].
При высоких частотах, когда $\omega {{\tau }_{0}} \gg 1,$ т.е. при $\omega \to \infty ,$ из (6) и (7) для динамических коэффициентов вязкости получим:
(9)
$\begin{gathered} {{{{\eta }}}_{s}}(\omega ) = - \frac{1}{\omega }\left( {\sum\limits_{i = f,s} {{{B}_{{si}}}} + \frac{{{{B}_{f}}}}{5}} \right), \\ {{\eta }_{{\text{v}}}}(\omega ) = \frac{1}{\omega }\left( {\sum\limits_{i = f,s} {\left( {{{K}_{{si}}} - (1 + {{\gamma }_{i}}){{n}_{i}}kT - {{B}_{{{\text{v}}i}}}} \right)} - \frac{{{{B}_{f}}}}{3}} \right), \\ \end{gathered} $Согласно (9), при высоких частотах динамические коэффициенты сдвиговой и объемной вязкости стремятся к нулю по закону ${{\omega }^{{ - 1}}}$ и по виду совпадают с высокочастотными модулями упругости [29, 30].
Теперь рассмотрим случай, когда релаксирующие потоки изменяются по экспоненциальному закону. Как известно, уравнение Больцмана и похожие на него кинетические уравнения позволяют получать уравнения сохранения, а также описывают релаксационные процессы, приводящие к максвелловскому равновесному состоянию. Однако большие трудности возникают при анализе интегралов столкновений в этих уравнениях. Кинетическое уравнение Бхатнагара–Гросса–Крука, обладая всеми этими свойствами, в то же время имеет достаточно простую структуру и позволяет избежать трудного анализа, связанного с больцмановским интегралом столкновений.
Теперь, с целью упрощения структуры уравнения Смолуховского (2), применяем аппроксимацию Бхатнагара–Гросса–Крука, т.е. релаксационный член Смолуховского ${{\omega }_{{0i}}}{{\hat {L}}_{i}}n_{{2i}}^{'}\left( {{{{\mathbf{q}}}_{1}},{\mathbf{r}},t} \right)$ заменяем релаксационным членом типа $\frac{{n_{{2i}}^{0}{\kern 1pt} \left( {\left| {\mathbf{r}} \right|,n,T} \right) - {{n}_{{2i}}}{\kern 1pt} \left( {{{{\mathbf{q}}}_{1}},{\mathbf{r}},t} \right)}}{{{{\tau }_{{0i}}}}}{\kern 1pt} ,$ где ${{n}_{{2i}}}{\kern 1pt} \left( {{{{\mathbf{q}}}_{1}},{\mathbf{r}},t} \right)$ = $n_{{2i}}^{0}{\kern 1pt} \left( {\left| {\mathbf{r}} \right|,n,T} \right){\kern 1pt} {\kern 1pt} + $ + $n_{{2i}}^{'}\left( {{{{\mathbf{q}}}_{1}},{\mathbf{r}},t} \right),$ ${{\tau }_{{0i}}}$ – время релаксации неравновесной бинарной плотности ${{n}_{{2i}}}\left( {{{{\mathbf{q}}}_{1}},{\mathbf{r}},t} \right)$ к ее локально-равновесному значению $n_{{2i}}^{0}\left( {\left| {\mathbf{r}} \right|,n({{{\mathbf{q}}}_{1}},t),T({{{\mathbf{q}}}_{1}},t)} \right)$ = = $n_{{2i}}^{0}(\left| {\mathbf{r}} \right|) + {{\tilde {n}}_{{2i}}}\left( {\left| {\mathbf{r}} \right|,n,T,t)} \right),$ $n_{{2i}}^{0}(\left| {\mathbf{r}} \right|) = n_{i}^{{\text{2}}}{{g}_{i}}(\left| {\mathbf{r}} \right|)$ – равновесная бинарная плотность, ${{\tilde {n}}_{{2i}}}\left( {\left| {\mathbf{r}} \right|,n,T,t)} \right)$ = = ${{\left( {\frac{{\partial n_{{2i}}^{0}(\left| {\mathbf{r}} \right|)}}{{\partial {{n}_{i}}}}} \right)}_{T}}{{n}_{i}}({{{\mathbf{q}}}_{1}},t)$ + ${{\left( {\frac{{\partial n_{{2i}}^{0}(\left| {\mathbf{r}} \right|)}}{{\partial T}}} \right)}_{{{{n}_{i}}}}}T({{{\mathbf{q}}}_{1}},t).$
Подставляя эти выражения в (2) и совершая фурье-преобразование по времени, с учетом уравнения гидродинамики в локально-равновесном приближении для фурье-образа неравновесной функции бинарной плотности получим:
(10)
$\begin{gathered} {{n}_{{2i}}}\left( {{{{\mathbf{q}}}_{1}},{\mathbf{r}},\omega } \right) = n_{i}^{2}{{g}_{i}}(r) - n_{i}^{2}\left[ {{{n}_{i}}{{{\left( {\frac{{\partial {{g}_{i}}(r)}}{{\partial {{n}_{i}}}}} \right)}}_{T}} + } \right. \\ \left. { + \,\,{{\gamma }_{i}}T{{{\left( {\frac{{\partial {{g}_{i}}(r)}}{{\partial T}}} \right)}}_{{{{n}_{i}}}}}} \right]{\text{div}}{\mathbf{u}} + \frac{{i\omega {{\tau }_{{0i}}}}}{{1 - i\omega {{\tau }_{{0i}}}}} \times \\ \times \,\,\left[ {{{\varphi }_{i}}(r) + \frac{{n_{i}^{2}{{\mu }_{0}}}}{{9{{\beta }_{i}}}}\left( {{\mathbf{m}}\nabla } \right){{{\left( {\frac{{\partial H}}{{\partial \upsilon }}} \right)}}_{{{{n}_{i}},T}}}r\left( {\frac{{\partial {{g}_{i}}(r)}}{{\partial r}}} \right)} \right]{\text{div}}{\mathbf{u}} + \\ + \,\,\frac{{i\omega {{\tau }_{{0i}}}}}{{1 - i\omega {{\tau }_{{0i}}}}}\varphi _{i}^{{\alpha \beta }}(r)\left[ {1 + \frac{{{{\mu }_{0}}}}{{3{{\beta }_{i}}}}\left( {{\mathbf{m}}\nabla } \right){{{\left( {\frac{{\partial H}}{{\partial \upsilon }}} \right)}}_{{{{n}_{i}},T}}}} \right]\left\{ {\frac{{\partial {{u}^{\alpha }}}}{{\partial q_{1}^{\beta }}}} \right\}. \\ \end{gathered} $Уравнение для $k_{i}^{{\alpha \beta }}\left( {{{{\mathbf{q}}}_{1}},t} \right),$ как показано в [17], получается из кинетического уравнения для одночастичной функции распределения и в линейном приближении имеет следующее решение:
(11)
$\begin{gathered} {{\eta }_{s}}\left( \omega \right) = \sum\limits_{i = f,s} {\frac{{{{n}_{i}}kT{{\tau }_{{1i}}}}}{{1 + {{{(\omega {{\tau }_{{1i}}})}}^{2}}}}} - \sum\limits_{i = f,s} {\frac{{{{\tau }_{{0i}}}}}{{1 + {{{(\omega {{\tau }_{{0i}}})}}^{2}}}}\frac{{n_{i}^{2}\sigma _{i}^{3}}}{{30}}} \times \\ \times \,\,\int\limits_0^\infty {\frac{{\partial {{\Phi }_{i}}}}{{\partial r}}\frac{{\partial {{g}_{i}}(r)}}{{\partial r}}{{r}^{2}}d{\mathbf{r}}} - \frac{{{{\tau }_{{0f}}}}}{{1 + {{{(\omega {{\tau }_{{0f}}})}}^{2}}}}\frac{{n_{f}^{2}\sigma _{f}^{3}}}{{90}} \times \\ \times \,\,\int\limits_0^\infty {\frac{{\partial {{\Phi }_{f}}}}{{\partial r}}\frac{{\partial {{g}_{f}}(r)}}{{\partial r}}\frac{{{{\mu }_{0}}}}{\beta }\left( {{\mathbf{m}}\nabla } \right)\frac{{\partial H}}{{\partial \upsilon }}{{r}^{2}}d{\mathbf{r}}} , \\ \end{gathered} $(12)
$\begin{gathered} {{\eta }_{{\text{v}}}}\left( \omega \right) = - \sum\limits_{i = f,s} {\frac{{{{\tau }_{{0i}}}}}{{1 + {{{(\omega {{\tau }_{{0i}}})}}^{2}}}}\frac{{n_{i}^{2}\sigma _{i}^{3}}}{6}} \int\limits_0^\infty {\frac{{\partial {{\Phi }_{i}}}}{{\partial r}}{{\varphi }_{i}}(r)rd{\mathbf{r}}} - \\ - \,\,\frac{{{{\tau }_{{0f}}}}}{{1 + {{{(\omega {{\tau }_{{0f}}})}}^{2}}}}\frac{{n_{f}^{2}\sigma _{f}^{3}}}{{54}}\int\limits_0^\infty {\frac{{\partial {{\Phi }_{f}}}}{{\partial r}}\frac{{\partial {{g}_{f}}(r)}}{{\partial r}}\frac{{{{\mu }_{0}}}}{\beta }\left( {{\mathbf{m}}\nabla } \right)\frac{{\partial H}}{{\partial \upsilon }}{{r}^{2}}d{\mathbf{r}}} . \\ \end{gathered} $ВЫБОР МОДЕЛИ И ЧИСЛЕННЫЕ РАСЧЕТЫ
Чтобы на основе выражений (6), (7), (11) и (12) провести численные расчеты, необходимо выбрать явный вид входящих в них потенциалов межчастичного взаимодействия ${{\Phi }_{i}}$ и соответствующие им радиальные функции распределения ${{g}_{i}}.$ В соответствии с [21], для молекулярной подсистемы применяем модель Штокмайера
(13)
${{\Phi }_{s}}({\mathbf{r}}) = \Phi _{s}^{{{\text{L - J}}}}(r) + {{\Phi }^{{pp}}}({\mathbf{r}}),$Считая феррочастицы сферическими однодоменными частицами, покрытыми слоем поверхностно-активного вещества и находящимися под действием внешнего магнитного поля, их взаимодействия для магнитной подсистемы представим в виде
(14)
${{\Phi }_{f}}({\mathbf{r}},{\mathbf{H}}) = \Phi _{f}^{{{\text{L - J}}}}(r) + {{\Phi }^{{mm}}}({\mathbf{r}}) + {{\Phi }^{H}}({\mathbf{H}}),$Электрическое и магнитное диполь-дипольные взаимодействия при переходе к сферической системе координат (рис. 1), представим в виде
(15)
${{\Phi }^{{dd}}}(r,{{\theta }_{a}},{{\theta }_{b}},{{\varphi }_{a}} - {{\varphi }_{b}}) = - {{A}^{d}}\frac{{{{d}^{2}}}}{{{{r}^{3}}}}\chi ({{\theta }_{a}},{{\theta }_{b}},{{\varphi }_{a}} - {{\varphi }_{b}}),$В магнитной подсистеме учет отталкивающей силы, возникающей при наличии слоя поверхностно-активного вещества, обеспечивается потенциалом Леннард-Джонса $\Phi _{f}^{{{\text{L - J}}}}(r).$ Хотя этот потенциал при описании взаимодействия коллоидных частиц широко используется, при определении значения глубины потенциальной ямы ${{\varepsilon }_{f}}$ возникает серьезная проблема. Например, согласно [31], в магнитной жидкости с магнитными частицами диаметром $10\,\,{\text{нм,}}$ покрытыми слоем поверхностно-активного вещества толщиной 2 нм, в отсутствие магнитного поля глубина минимума энергии равна $0.3kT.$ При наличии внешнего магнитного поля глубина минимума составляет $0.9kT.$
Радиальные функции распределения для каждой подсистемы выбираем в виде
(16)
$\begin{gathered} {{g}_{s}}(r,{{n}_{s}},T) = {{y}_{s}}(\rho {\kern 1pt} *)\exp \left[ {{{ - {{\Phi }_{s}}({\mathbf{r}})} \mathord{\left/ {\vphantom {{ - {{\Phi }_{s}}({\mathbf{r}})} {kT}}} \right. \kern-0em} {kT}}} \right], \\ {{g}_{f}}(r,T,H) = \exp \left[ {{{ - {{\Phi }_{f}}({\mathbf{r}},{\mathbf{H}})} \mathord{\left/ {\vphantom {{ - {{\Phi }_{f}}({\mathbf{r}},{\mathbf{H}})} {kT}}} \right. \kern-0em} {kT}}} \right]. \\ \end{gathered} $Необходимо отметить, что непосредственная подстановка потенциалов (13) и (14) в выражения для коэффициентов вязкости приводит к неразрешимым математическим трудностям. Поэтому для упрощения задачи после перехода к сферической системе координат, следуя работам [32, 33], для двух ближайших частиц момент первой частицы принимаем вдоль радиус-вектора, соединяющего ее со второй частицей (рис. 1). Соответственно в (15), положив ${{\theta }_{a}} = 0,$ ${{\theta }_{b}} = \theta $ (рис. 1), энергию взаимодействия двух диполей выражаем в виде
Аналогично, направляя напряженность внешнего магнитного поля ${\mathbf{H}}$ параллельно оси $z$ системы, для потенциальной энергии взаимодействия магнитного диполя с внешним полем получим: Таким образом, подставляя выражения (13)–(16) в (6) и (7), приведем их к виду, удобному для проведения численных расчетов:(17)
${{\eta }_{s}}\left( \omega \right) = \sum\limits_{i = f,s} {\frac{{{{n}_{i}}kT{{\tau }_{{1i}}}}}{{1 + {{{(\omega {{\tau }_{{1i}}})}}^{2}}}}} + \sum\limits_{i = f,s} {\frac{{4{{\varepsilon }_{i}}n_{i}^{2}\sigma _{i}^{3}}}{{kT}}{{J}_{{si}}}} ,$(18)
${{\eta }_{{\text{v}}}}\left( \omega \right) = \sum\limits_{i = f,s} {\frac{{4{{\varepsilon }_{i}}n_{i}^{2}\sigma _{i}^{3}}}{{kT}}{{J}_{{{\text{v}}i}}}} ,$Выражения (13)–(16) подставим в (11) и (12) и приведем их к виду
(19)
${{\eta }_{s}}\left( \omega \right) = \sum\limits_{i = f,s} {\frac{{{{n}_{i}}kT{{\tau }_{{1i}}}}}{{1 + {{{(\omega {{\tau }_{{1i}}})}}^{2}}}}} + \sum\limits_{i = f,s} {\frac{{{{\tau }_{{0i}}}}}{{1 + {{{(\omega {{\tau }_{{0i}}})}}^{2}}}}\frac{{n_{i}^{2}\sigma _{i}^{3}}}{{5kT}}{{I}_{{si}}}} ,$(20)
${{\eta }_{{\text{v}}}}\left( \omega \right) = \sum\limits_{i = f,s} {\frac{{{{\tau }_{{0i}}}}}{{1 + {{{(\omega {{\tau }_{{0i}}})}}^{2}}}}\frac{{n_{i}^{2}\sigma _{i}^{3}}}{{kT}}{{I}_{{{\text{v}}i}}}} ,$Далее на основе выражений (17)–(20) проведен численный расчет динамических коэффициентов вязкости магнитных жидкостей с частицами Fe3O4 при $m = {{10}^{{ - 20}}}\,\,{{{\text{Дж}}} \mathord{\left/ {\vphantom {{{\text{Дж}}} {{\text{Тл}}}}} \right. \kern-0em} {{\text{Тл}}}}{\text{,}}$ ${{\sigma }_{f}} = 5\,\,{\text{нм,}}$ ${{\rho }_{f}} = 5340\,\,{{{\text{кг}}} \mathord{\left/ {\vphantom {{{\text{кг}}} {{{{\text{м}}}^{{\text{3}}}},}}} \right. \kern-0em} {{{{\text{м}}}^{{\text{3}}}},}}$ ${{\varepsilon }_{f}} = 0.37kT,$ приготовленных на основе керосина (${{\sigma }_{s}} = 0.43\,\,{\text{нм,}}$ ${{\rho }_{s}} = 819\,\,{{{\text{кг}}} \mathord{\left/ {\vphantom {{{\text{кг}}} {{{{\text{м}}}^{{\text{3}}}}}}} \right. \kern-0em} {{{{\text{м}}}^{{\text{3}}}}}},$ ${{\varepsilon }_{s}} = 0.6kT,$ $\varepsilon = 2.1,$ $p = 8.3 \times {{10}^{{ - 30}}}$ Кл м) и воды (${{\sigma }_{s}} = 0.27\,{\text{нм,}}$ ${{\rho }_{s}} = 1000\,\,{{{\text{кг}}} \mathord{\left/ {\vphantom {{{\text{кг}}} {{{{\text{м}}}^{{\text{3}}}}}}} \right. \kern-0em} {{{{\text{м}}}^{{\text{3}}}}}},$ ${{\varepsilon }_{s}} = 1.27kT,$ $\varepsilon = 81,$ $p = 6.2 \times {{10}^{{ - 30}}}$ Кл м), в широком диапазоне изменения гидродинамической частоты и при различных значениях внешнего магнитного поля.
На рис. 2–5 представлены результаты численных расчетов частотной зависимости динамических коэффициентов вязкости для магнитных жидкостей, приготовленных на основе керосина или воды и частиц Fe3O4, при $T = 298\,\,{\text{К}}$ и соответствующих значениях физических параметров, приведенных в табл. 1.
Рис. 2.
Зависимости ηs от частоты для магнитной жидкости на основе керосина при $\varphi = 0.05$ (1, 2) и $\varphi = 0.1$ (3, 4).

Рис. 3.
Зависимости ηs от частоты для магнитной жидкости на основе воды при $\varphi = 0.05$ (1, 2) и $\varphi = 0.1$ (3, 4).

Рис. 4.
Зависимости ηv от частоты для магнитной жидкости на основе керосина при $\varphi = 0.05$ (1, 2) и $\varphi = 0.1$ (3, 4).
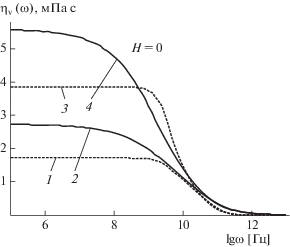
Рис. 5.
Зависимости ηv от частоты для магнитной жидкости на основе воды при $\varphi = 0.05$ (1, 2) и $\varphi = 0.1$ (3, 4).

Таблица 1.
Численные значения времен релаксации для магнитных жидкостей
| Магнитная жидкость | ${{\tau }_{{1s}}} \times {{10}^{{12}}},{\text{ с}}$ | ${{\tau }_{{0s}}} \times {{10}^{{10}}},{\text{ с}}$ | ${{\tau }_{{1f}}} \times {{10}^{{12}}},{\text{ с}}$ | ${{\tau }_{{0f}}} \times {{10}^{{10}}},{\text{ с}}$ | $H,{\text{ }}{{{\text{кА}}} \mathord{\left/ {\vphantom {{{\text{кА}}} {\text{м}}}} \right. \kern-0em} {\text{м}}}$ |
|---|---|---|---|---|---|
| На основе керосина | 1.05 | 0.2 | 5.49 | 2.06 | 0 |
| 1.05 | 0.2 | 2.93 | 3.87 | 200 | |
| На основе воды | 0.37 | 0.05 | 3.49 | 3.25 | 0 |
| 0.37 | 0.05 | 2.11 | 5.37 | 200 |
На всех рисунках сплошные кривые соответствуют выражениям (19), (20), а пунктирные – выражениям (21), (22). На рис. 2 и 3 приведены результаты расчетов коэффициента сдвиговой вязкости при отсутствии внешнего магнитного поля и когда значение напряженности поля равно 200 кА/м. На рис. 4 и 5 приведены результаты численных расчетов коэффициента объемной вязкости в отсутствие внешнего магнитного поля.
Видно, что во всех случаях область частотной дисперсии коэффициентов вязкости, вычисленных по выражениям (21) и (22), является узкой, как и наблюдается в экспериментах [22, 23], и не превышает двух декад. Напротив, результаты вычислений, проведенных на основе выражений (19) и (20), указывают на широкую область частотной дисперсии коэффициентов вязкости, составляющую пять декад и более. Однако для фиксированной частоты значения коэффициентов вязкости, полученные на основе выражений (19), (20), всегда больше, чем полученные на основе выражений (21) и (22). Видимо, это связано с более полным учетом вклада структурной релаксации, происходящей по диффузионным законам.
Как известно, при исследовании частотной зависимости коэффициентов переноса и акустических параметров наибольшее изменение этих величин всегда соответствует тем значениям частоты, которые близки к значению частоты релаксации ${{\omega }_{{\text{r}}}} = {1 \mathord{\left/ {\vphantom {1 \tau }} \right. \kern-0em} \tau }.$ В выражениях (19)–(22) фигурируют два времени: время трансляционной релаксации частиц ${{\tau }_{{1i}}} = {{{{m}_{i}}} \mathord{\left/ {\vphantom {{{{m}_{i}}} {2{{\beta }_{i}}}}} \right. \kern-0em} {2{{\beta }_{i}}}}$ и феноменологическое время структурной релаксации ${{\tau }_{{0i}}} = {{{{\beta }_{i}}\sigma _{i}^{2}} \mathord{\left/ {\vphantom {{{{\beta }_{i}}\sigma _{i}^{2}} {2kT}}} \right. \kern-0em} {2kT}}.$ Оба времени релаксации определяются через коэффициент трения $\beta ,$ который тесно связан с параметрами состояния и межмолекулярными силами в системе. Отметим, что проблема определения коэффициента $\beta $ на основе статистических методов до сих пор остается нерешенной, но для его нахождения исследователями предложены несколько моделей, рассмотренных в [34]. На основе анализа, проведенного в [34], было установлено, что значения, полученные для коэффициента трения магнитной жидкости на основе выражения
(21)
$\begin{gathered} \beta _{i}^{2} = 160\pi {{\rho }_{i}}{{\varepsilon }_{i}}{{\sigma }_{i}}\int\limits_0^\infty {{{g}_{{0i}}}(r)(4.4{{r}^{{ - 12}}} - {{r}^{{ - 6}}})\frac{{{\text{sh}}{{a}_{i}}}}{{{{a}_{i}}}}dr + } \\ + \,\,\frac{{16\pi {{\rho }_{i}}{{\sigma }_{i}}kT}}{3}\int\limits_0^\infty {{{g}_{{0i}}}(r)\left( {{\text{сh}}{{a}_{i}} - \frac{{{\text{sh}}{{a}_{i}}}}{{{{a}_{i}}}}} \right)dr} . \\ \end{gathered} $Согласно [22], если система релаксирует по нескольким механизмам со значительно различающимися временами релаксации, то кривые, описывающие частотные зависимости коэффициентов переноса, имеют ступенчатую форму с явно выраженными областями дисперсии. Поскольку для магнитной жидкости на основе воды ${{\tau }_{{0f}}}$ почти на два порядка больше, чем ${{\tau }_{{0s}}},$ то на кривых рис. 3 и 5, вычисленных на основе (21) и (22), можно наблюдать две отдельные области дисперсии. На рис. 6 в относительно большом масштабе приведены кривые частотной зависимости ${{\eta }_{s}}(\omega )$ для магнитной жидкости на основе воды, которые наглядно свидетельствуют о существовании отдельных областей дисперсии. Для кривых, вычисленных на основе (19) и (20), вследствие медленного изменения функции Грина области дисперсии перекрываются и такое разделение не наблюдается.
Рис. 6.
Зависимости ηs от частоты для магнитной жидкости на основе воды. $H = 0,$ $T = 298\,\,{\text{К}}{\text{.}}$

Для сравнения на рис. 7 приведен график из работы [35], где представлены результаты теоретических расчетов частотной зависимости реальной и мнимой частей комплексной динамической сдвиговой вязкости и их сравнение с экспериментальными результатами [36] для суспензий частиц кремнезема, диспергированных в циклогексане.
Рис. 7.
Результаты работы [35] по зависимости реальной и мнимой частей комплексной динамической сдвиговой вязкости от приведенной частоты.

В теории авторов [35] динамическая вязкость определяется функцией памяти ${{\hat {M}}_{\nu }}(\omega )$ = $ = \int_0^\infty {{{e}^{{i\omega t}}}{{M}_{\nu }}(t)dt} ,$ временнóй спектр ${{\tau }_{M}} = \int_0^\infty {t{{M}_{\nu }}(t)dt} $ которой характеризует скорость ее изменения, имеет длинный хвост, пропорциональный ${{t}^{{{{ - 7} \mathord{\left/ {\vphantom {{ - 7} 2}} \right. \kern-0em} 2}}}}.$ В согласии с этим, при низких частотах функция памяти, а соответственно и динамическая вязкость, имеет асимптотику, пропорциональную ${{\omega }^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$ При высоких частотах динамическая вязкость изменяется по закону ${{\omega }^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}},$ и при $\omega \to \infty $ имеет место закон ${1 \mathord{\left/ {\vphantom {1 \omega }} \right. \kern-0em} \omega }.$
Таким образом, можно заключить, что асимптотическое поведение динамических коэффициентов вязкости, полученных нами на основе диффузионного закона затухания релаксирующих потоков, полностью совпадает с теоретическими результатами [35], описывающими поведение коллоидных суспензий.
ЗАКЛЮЧЕНИЕ
В работе исследована частотная зависимость динамических коэффициентов сдвиговой и объемной вязкости, полученных двумя путями на основе: 1) вывода уравнения Смолуховского в конфигурационном пространстве, полностью описывающего пространственно-временнóе поведение функции бинарной плотности; 2) аппроксимации Бхатнагара–Гросса–Крука, приводящей к экспоненциальному затуханию релаксационных процессов. Показано, что в первом случае область частотной дисперсии коэффициентов вязкости является широкой и составляет пять декад, как для некоторых вязких масел [22]. Во втором случае область частотной дисперсии получается узкой, составляя две декады, что наблюдается в многочисленных экспериментах для разных жидкостей.
Список литературы
Alder B.J., Wainwright T.E. // Phys. Rev. 1970. V. 1. P. 18.
Zwanzig R., Bixon M. // Phys. Rev. 1970. V. 2. P. 2005.
Ernst M.H., Hauge E.H., Van Leeuwen J.M.J. // Phys. Rev. Lett. 1970. V. 25. P. 1254.
Ernst M.H., Hauge E.H., Van Leeuwen J.M.J. // Phys. Rev. A. 1971. V. 4. P. 2055.
Dorfman J.R., Cohen E.G.D. // Phys. Rev. Lett. 1970. V. 25. P. 1257.
Фишер И.З. // ЖЭТФ. 1971. Т. 61. С. 1647.
Pomeau Y., Resibois P. // Phys. Rep. 1975. V. 19C. P. 63.
Резибуа П., Де Ленер М. Классическая кинетическая теория жидкостей и газов. М.: Мир, 1980.
Lokotosh T.V., Malomuzh N.P. // Physica A. 2000. V. 286. P. 474.
Bulavin A., Lokotosh T.V., Malomuzh N.P. // J. Mol. Liq. 2008. V. 137. P. 1.
Волошин В.П., Маленков Г.Г., Наберухин Ю.И. // Журн. структ. химии. 2013. Т. 54. № S2. С. 239.
Лагарьков Л.Н., Сергеев В.М. // УФН. 1978. Т. 125. С. 409.
Levesque D., Ashurst W.T. // Phys. Rev. Lett. 1974. V. 33. P. 277.
Dib R.F.A., Ould-Kaddour F., Levesque D. // Phys. Rev. E. 2006. V. 74. P. 011202-1.
Рудяк В.Я., Харламов Г.В., Белкин А.А. // Письма в ЖТФ. 2000. Т. 26. № 13. С. 29.
Рудяк В.Я., Харламов Г.В., Белкин А.А. // ТВТ. 2001. Т. 39. С. 283.
Одинаев С., Комилов К., Зарифов А. // Журн. физ. химии. 2006. Т. 80. С. 864.
Одинаев С., Комилов К., Зарипов А. // ДАН РТ. 2008. Т. 51. С. 107.
Odinaev S., Komilov K., Zaripov A. // Ukr. J. Phys. 2008. V. 53. P. 234.
Одинаев С., Комилов К., Зарипов А. // Журн. физ. химии. 2008. Т. 82. С. 1120.
Комилов К., Зарипов А., Убайди А. // Журн. физ. химии. 2020. Т. 94. С. 1279.
Михайлов И.Г., Соловьев В.А., Сырников Ю.П. Основы молекулярной акустики. М.: Наука, 1964.
Полунин В.М. Акустические свойства нанодисперсных магнитных жидкостей. М.: Физматлит, 2012.
Kirkwood J.G., Buff F.P., Green M.S. // J. Chem. Phys. 1949. V. 17. P. 988.
Ландау Л.Д., Лифшиц Е.М. Механика сплошных сред. М.: Гостехтеоретиздат, 1953.
Evans D.J. // J. Stat. Phys. 1980. V. 22. P. 81.
Zwanzig R. // Proc. Natl. Acad. Sci. USA. 1981. V. 78. P. 3296.
Эванс Д.Дж., Хенли Г.Дж., Гесс З. // Физика за рубежом. Серия А. Исследования. М.: Мир, 1986. С. 7.
Lemberg H.L., Stillinger F.H. // J. Chem. Phys. 1975. V. 62. P. 1677.
Zwanzig R., Mountain R.D. // J. Chem. Phys. 1965. V. 43. P. 4464.
Берковский Б.М., Медведев В.Ф., Краков М.С. Магнитные жидкости. М.: Химия, 1989.
Литинский Г.Б. // Журн. структ. химии. 2004. Т. 45. С. 86.
Менделев В.С. Магнитные свойства феррожидкостей с цепочечными агрегатами. Дис. … канд. физ.-мат. наук. Екатеринбург: Уральский государственный университет им. А.М. Горького, 2009.
Комилов К., Зарипов А.К. // Вестник фил. МГУ им. М.В. Ломоносова в г. Душанбе. 2018. № 1(2). С. 64.
Cichocki B., Felderhof B.U. // J. Chem. Phys. 1994. V. 101. P. 7850.
Van der Werff J.C., De Kruif C.G. // Phys. Rev. 1989. V. 39. P. 795.
Дополнительные материалы отсутствуют.
Инструменты
Коллоидный журнал



