Коллоидный журнал, 2021, T. 83, № 5, стр. 524-531

ВВЕДЕНИЕ

Недавно [1–3] нами в рамках градиентного приближения метода функционала молекулярной плотности были проведены расчеты равновесных профилей плотности и других локальных и интегральных термодинамических характеристик для плоских и сферических паровых прослоек вблизи лиофобных твердых поверхностей, находящихся в контакте с жидкой фазой. В результате этих расчетов было показано, что наряду с равновесными профилями плотности, отвечающими седловой точке большого термодинамического потенциала всей системы подложка–прослойка–жидкая фаза, в определенном интервале значений химического потенциала флюида существуют и равновесные профили, соответствующие минимуму большого термодинамического потенциала системы.

Равновесные профили плотности флюида, отвечающие седловой точке большого термодинамического потенциала системы, характеризуют неустойчивое равновесие паровых прослоек вокруг лиофобных частиц. Эти паровые оболочки играют роль критических зародышей газовой фазы при заданном значении химического потенциала молекул флюида и имеют малое время жизни. Равновесные профили плотности, отвечающие минимуму большого термодинамического потенциала системы, характеризуют устойчивое равновесие паровых прослоек вокруг лиофобных частиц. Такие прослойки могут существовать как угодно долго, в том числе, и в нерастянутой жидкости. В [1] было показано, что в растянутой жидкости существует предельное значение химического потенциала молекул жидкой фазы, при котором и ниже которого начинается безбарьерная нуклеация пузырьков пара вокруг лиофобных частиц заданного размера.

Полученные в [1–3] результаты для устойчивых и неустойчивых зародышей газовой фазы согласуются с более ранними общими термодинамическими предсказаниями на основе анализа роли расклинивающего давления в тонких неоднородных пленках [4, 5] и теории гетерогенной нуклеации на смачиваемых ядрах конденсации [6–10].

Сам по себе градиентный вариант метода функционала молекулярной плотности является хорошо проверенным инструментом теоретического исследования неоднородных систем с поверхностными слоями между твердой, жидкой и газовой фазами [11–16]. Используемый в [1–3] подход опирался на ранее полученные в рамках такого же метода результаты [17–21] для профилей молекулярной плотности, расклинивающего давления, поверхностного натяжения и большого термодинамического потенциала в случае тонких жидких пленок вокруг лиофильных твердых частиц.

Однако в рамках градиентного метода функционала молекулярной плотности в его приложении к очень тонким паровым прослойкам все же остается ряд принципиальных вопросов. Эти вопросы связаны с граничными условиями на профиль плотности вблизи твердой поверхности [12, 22–27], с погрешностью градиентного метода в зависимости от толщины прослойки, с ролью явного представления для межмолекулярного потенциала. Ответы на эти вопросы были получены в данном сообщении в рамках исследования экстремумов большого термодинамического потенциала системы с помощью метода упругой ленты [28–32] и интегрального метода функционала плотности [33–38].

1. ПРИМЕНЕНИЕ МЕТОДА УПРУГОЙ ЛЕНТЫ К ЗАДАЧЕ О ПАРОВОЙ ОБОЛОЧКЕ ВОКРУГ ЛИОФОБНОЙ ЧАСТИЦЫ

В последнее время эффективно развивается вычислительный метод подталкивания упругой ленты (Nudged Elastic Band, NEB [28–32]) в применении к задачам, где требуется анализ энергетической гиперповерхности в пространстве с большим или бесконечным числом степеней свободы. Этот численный метод позволяет найти путь минимального перепада энергии (ПМПЭ или Minimum Energy Path, MEP в англоязычной литературе), который “проходит” система от исходного нестабильного состояния к конечному, стабильному.

В приложении к задаче нуклеации метод упругой ленты – это способ исследования рельефа большого термодинамического потенциала как функционала на пространстве профилей плотности через оптимизацию цепочек состояний системы, которые характеризуются принимаемыми в них значениями этого потенциала при переходе от состояния исходной метастабильной фазы к конечному состоянию с частицей новой фазы [31, 36, 37]. В этом подходе решения соответствующего уравнения Эйлера не требуются.

Возьмем в качестве функционала молекулярной плотности следующее выражение для большого термодинамического потенциала флюидной системы с паровой оболочкой вокруг лиофобной твердой сферической частицы-ядра:

Это выражение записано в рамках градиентного приближения (см. [1–3]) с использованием модели Карнахана–Старлинга для вклада твердых сфер во взаимодействие молекул флюида. Здесь $\rho \left( {\vec {r}} \right)$ – локальная плотность флюида в точке, задаваемой радиусом $\vec {r}$ в системе координат, центр которой совпадает с центром твердого ядра, ${{k}_{{\text{B}}}}$ – постоянная Больцмана, $T$ – абсолютная температура системы, ${{\lambda }_{{{\text{th}}}}} = \hbar \sqrt {{{2\pi } \mathord{\left/ {\vphantom {{2\pi } {(m{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {(m{{k}_{{\text{B}}}}T}})} $ – тепловая длина волны де Бройля ($\hbar $ – постоянная Планка, $m$ – масса молекулы флюида), $\eta = {{\pi {{d}^{3}}\rho } \mathord{\left/ {\vphantom {{\pi {{d}^{3}}\rho } 6}} \right. \kern-0em} 6}$ – безразмерная молекулярная плотность флюида ($d$ – диаметр молекулы в модели твердых сфер). Коэффициент $a$ – параметр притяжения молекул флюида в приближении среднего поля, который связан с модельным межмолекулярным потенциалом и, в частности, с энергетическим параметром Леннард-Джонса ${{\varepsilon }_{{{\text{ff}}}}}$ для молекул флюида, $C$ – параметр, зависящий от температуры $T$ и связанный с поверхностным натяжением $\gamma _{\infty }^{{{\text{GL}}}}$ на плоской границе жидкой и газовой фаз (может быть приближенно вычислен как $C = 14.00{{\sigma }^{5}}{{k}_{{\text{B}}}}T$), $\mu $ – химический потенциал молекул флюида. Интегрирование в (1) не включает объем частицы. Функция ${{w}_{{{\text{pf}}}}}(r)$ является полным потенциалом взаимодействия ядра с молекулой флюида (интегральная сумма взаимодействий со всеми молекулами ядра) и может быть записана в виде

где ${{\varepsilon }_{{{\text{pf}}}}}$ – энергетический параметр Леннард-Джонса для взаимодействия молекул твердого тела и флюида, ${{\rho }_{{\text{p}}}}$ – средняя молекулярная плотность твердого тела, ${{R}_{{\text{p}}}}$ – радиус ядра. Чтобы учесть лиофобность ядра, возьмем ${{\rho }_{{\text{p}}}} = 1.07 \times {{10}^{{27}}}\,\,{{{\text{м}}}^{{ - 3}}}$ (плотность парафина) и рассмотрим значения отношения энергетических параметров $\frac{{{{\varepsilon }_{{{\text{pf}}}}}}}{{{a \mathord{\left/ {\vphantom {a {{{\sigma }^{3}}}}} \right. \kern-0em} {{{\sigma }^{3}}}}}}$ меньше единицы. Заметим, что $\sigma \,$ в общем случае не совпадает с параметром потенциала Леннард-Джонса для молекул флюида.

В [1] равновесный профиль плотности ${{\rho }^{{\left( {\text{e}} \right)}}}\left( r \right)$ был найден из условия стационарности ${{\left. {{{\delta {{\Omega }^{{{\text{pf}}}}}} \mathord{\left/ {\vphantom {{\delta {{\Omega }^{{{\text{pf}}}}}} {\delta \rho \left( r \right)}}} \right. \kern-0em} {\delta \rho \left( r \right)}}} \right|}_{{{{\rho }^{{\left( {\text{e}} \right)}}}}}} = 0$, которое приводит к дифференциальному уравнению на равновесный профиль плотности:

В качестве краевых условий были взяты равенства ${{\rho }^{{\left( {\text{e}} \right)}}}\left( {{{R}_{{\text{p}}}} + {d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}} \right) = 0$ и ${{\left. {{{\rho }^{{\left( {\text{e}} \right)}}}\left( r \right)} \right|}_{{r \to \infty }}} = {{\rho }^{{\text{L}}}}$, где ${{\rho }^{{\text{L}}}}$ – объемная плотность жидкой фазы при заданном химическом потенциале. Главной задачей этого раздела является сравнение полученных в результате решения уравнения (3) локальных профилей плотности ${{\rho }^{{\left( {\text{e}} \right)}}}\left( r \right)$ из [1] с профилями, отвечающими стационарным точкам ${{\Omega }^{{{\text{pf}}}}}$, определенным с помощью метода упругой ленты.

Итак, найдем ПМПЭ при заданном химическом потенциале $\mu < {{\mu }_{\infty }}$ (здесь ${{\mu }_{\infty }}$ – значение химического потенциала при равновесии в случае плоской межфазной поверхности жидкость–пар). Следуя [32, 37], применим метод упругой ленты в форме [29] с модификацией “восходящей картинки” (climbing image в англоязычной литературе) [28] (для проработки минимума и максимума ПМПЭ, пояснение будет дано ниже) с использованием движка FIRE [30], который отличается простотой и эффективностью в сравнении с другими методами в приложении к методу упругой ленты [31]. В методе упругой ленты требуется задать начальное приближение для ПМПЭ в виде цепочки состояний системы (“картинок”). Это приближение для нашей задачи может быть задано как последовательность профилей вида [32]

где $i = 2...N,$ $N$ – число картинок, ${{\rho }^{{\text{L}}}}$ и ${{\rho }^{{\text{G}}}}$ – объемные плотности жидкой и газовой фазы при заданном химическом потенциале, ${{r}_{i}}$ – примерный радиус пузырька на i-й картинке, который увеличивается с ростом i; первая картинка представляет собой состояние однородной жидкости. Радиусы пузырьков были подобраны в виде ${{r}_{i}} \equiv {{R}_{{\text{p}}}} + 0.75\frac{{i + 1}}{{N - 1}}l$, где $l \equiv 15\sigma $ – достаточно большое расстояние, чтобы все профили выходили на плато ${{\rho }_{i}}(r)\sim {{\rho }^{{\text{L}}}}$ при $r\sim {{R}_{{\text{p}}}} + l$ и в цепочке был хорошо виден максимум $\Omega _{{}}^{{{\text{pf}}}}$.

В методе упругой ленты на  i-ю картинку действует “потенциальная сила” $F_{i}^{{{\text{pot}}}} \equiv $ ${{\left. {{{ - \delta {{\Omega }^{{{\text{pf}}}}}} \mathord{\left/ {\vphantom {{ - \delta {{\Omega }^{{{\text{pf}}}}}} {\delta \rho \left( r \right)}}} \right. \kern-0em} {\delta \rho \left( r \right)}}} \right|}_{{{{\rho }_{i}}}}},$ а также искусственно введенная упругая сила $F_{i}^{{\text{s}}} \equiv k\left( {{{\rho }_{{i + 1}}}\left( r \right) - {{\rho }_{i}}\left( r \right)} \right)$ – $k\left( {{{\rho }_{i}}\left( r \right) - {{\rho }_{{i - 1}}}\left( r \right)} \right)$, которая обеспечивает равномерное распределение картинок вдоль ПМПЭ (здесь $k$ – жесткость “пружинок”, связывающих картинки). Чтобы исключить влияние искусственно введенных пружинок на ПМПЭ и влияние потенциальных сил на распределение картинок вдоль пути, учитываются только параллельная проекция (на путь) упругих сил и перпендикулярная проекция потенциальных сил. В итоге, сила, действующая на i-ю картинку, равна ${{F}_{i}} \equiv {{\left. {F_{i}^{{\text{s}}}} \right|}_{{||}}} + {{\left. {F_{i}^{{{\text{pot}}}}} \right|}_{ \bot }}$. Под действием таких сил цепочка картинок движется к ПМПЭ; выполнение алгоритма прекращается при достижении достаточной малости среднеквадратичной силы ${{\left. {F_{i}^{{{\text{pot}}}}} \right|}_{ \bot }}$. Таким образом, метод дает ПМПЭ, удовлетворяющий уравнениям $\left\| {{{{\left. {{{{\left. {{{\delta {{\Omega }^{{{\text{pf}}}}}} \mathord{\left/ {\vphantom {{\delta {{\Omega }^{{{\text{pf}}}}}} {\delta \rho \left( r \right)}}} \right. \kern-0em} {\delta \rho \left( r \right)}}} \right|}}_{{{{\rho }_{i}}}}}} \right|}}_{ \bot }}} \right\| = 0,$ $i = 1...N$ с заданной точностью (в качестве нормы была выбрана ${{L}^{2}}$-норма). В данной работе использовался улучшенный метод (см. раздел IV в [29]), который позволяет избежать появления изгибов на ПМПЭ.

Упругие силы не определены для первой и последней картинок, поэтому слева на первую картинку и справа на последнюю действовали силы-константы, которые подбирались соразмерными другим упругим силам $F_{i}^{{\text{s}}}$. Можно было бы фиксировать первую картинку (однородная жидкость), но она имеет очень низкое значение ${{\Omega }^{{{\text{pf}}}}}$ вследствие неточности градиентного приближения для ${{\Omega }^{{{\text{pf}}}}},$ которую мы обсудим в разделе 2. В связи с этим лучшие (в смысле нахождения устойчивого профиля) результаты показал метод упругой ленты, в котором первая картинка не была фиксирована, а двигалась в процессе релаксации цепочки состояний к ПМПЭ, как и другие картинки. Последняя картинка тоже не была фиксирована, так как конечное состояние системы – состояние пара – находится бесконечно далеко от остальных картинок цепочки (с пузырьками конечного радиуса) [32].

Чтобы одна из картинок попала точно в максимум ПМПЭ, для нее сила берется в виде ${{F}_{{{{i}_{{\max }}}}}} \equiv - {{\left. {F_{{{{i}_{{\max }}}}}^{{{\text{pot}}}}} \right|}_{{||}}} + {{\left. {F_{{{{i}_{{\max }}}}}^{{{\text{pot}}}}} \right|}_{ \bot }}$; такая картинка называется восходящей [28], она “забирается” на максимум благодаря такому выбору параллельной проекции силы, действующей на нее. Аналогично, для поиска минимума возьмем силу в виде ${{F}_{{{{i}_{{\min }}}}}} \equiv {{\left. {F_{{{{i}_{{\min }}}}}^{{{\text{pot}}}}} \right|}_{{||}}} + {{\left. {F_{{{{i}_{{\min }}}}}^{{{\text{pot}}}}} \right|}_{ \bot }} = F_{{{{i}_{{\min }}}}}^{{{\text{pot}}}}$. Также для лучшей проработки минимума был рассмотрен отрезок пути от однородной фазы до седловой точки (которая уже была получена) с обоими закрепленными концами с большей плотностью картинок.

Как видно на рис. 1, кривая ПМПЭ имеет локальные минимум и максимум, соответствующие минимуму и седловой точке функционала ${{\Omega }^{{{\text{pf}}}}}$. Таким образом, устойчивый пузырек пара вокруг лиофобной частицы существует и в методе упругой ленты.

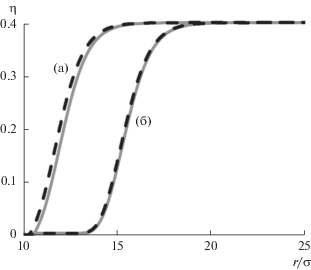
На рис. 2 приведено сравнение равновесных профилей плотности, соответствующих экстремумам на кривой ПМПЭ и полученным в [1] решениям дифференциального уравнения (3) в градиентном методе функционала плотности. Согласие двух методов хорошее, так как относительное различие величин ${{\Omega }^{{{\text{pf}}}}}$ в минимуме и седловой точке, полученных обоими методами, не превосходит 0.001. Отметим, что граничные условия в методе упругой ленты не задаются, но полученные в рамках этого метода профили плотности в результате удовлетворяют граничным условиям ${{\rho }^{{\left( {\text{e}} \right)}}}\left( {{{R}_{{\text{p}}}} + {d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}} \right) = 0$ и ${{\left. {{{\rho }^{{\left( {\text{e}} \right)}}}\left( r \right)} \right|}_{{r \to \infty }}} = {{\rho }^{{\text{L}}}}$.

В работе [39] в рамках метода упругой ленты была рассмотрена более общая задача о нахождении равновесных профилей пузырьков на твердых частицах произвольной лиофобности. В этом исследовании не было обнаружено минимума в виде пузырька на полученной кривой ПМПЭ. Следует, однако, заметить, что в [39] был использован нелокальный интегральный метод функционала плотности совместно с учетом корреляций твердых сфер. Чтобы убедиться, что наличие минимума не является артефактом градиентного метода функционала плотности, найдем в разделе 2 профили плотности для свободного концентрического пузырька вокруг лиофобной частицы с помощью интегрального метода.

2. ПРОФИЛИ ПЛОТНОСТИ В ПАРОВОЙ ОБОЛОЧКЕ ВОКРУГ ЛИОФОБНОЙ ЧАСТИЦЫ В РАМКАХ ИНТЕГРАЛЬНОГО МЕТОДА ФУНКЦИОНАЛА ПЛОТНОСТИ

В приближении случайной фазы (random phase approximation в англоязычной литературе) большой термодинамический потенциал ${{\Omega }^{{{\text{pf}}}}}$ для системы частица–оболочка–жидкость в интегральном методе функционала плотности может быть представлен [33, 34] как

Здесь, в пренебрежении корреляциями твердых сфер, которые не должны быть существенны для образования пузырьков на лиофобных частицах, вклад в свободную энергию ${{F}_{{\text{h}}}}\left[ {\rho \left( {\vec {r}} \right)} \right]$ твердых сфер в модели Карнахана–Старлинга остается, как и в (1), равным ${{F}_{{\text{h}}}}\left[ {\rho \left( {\vec {r}} \right)} \right]$ = = ${{k}_{{\text{B}}}}T\int_V {\rho \left[ {ln(\lambda _{{{\text{th}}}}^{3}\rho ) - 1 + \frac{{4\eta - 3{{\eta }^{2}}}}{{{{{(1 - \eta )}}^{2}}}}} \right]d\vec {r}} $; $w(\left| {\vec {r} - \vec {r}{\kern 1pt} '} \right|)$ – центральный потенциал притяжения между молекулами флюида.

Уравнение ${{\left. {{{\delta {{\Omega }^{{{\text{pf}}}}}\left[ {\rho \left( {\vec {r}} \right)} \right]} \mathord{\left/ {\vphantom {{\delta {{\Omega }^{{{\text{pf}}}}}\left[ {\rho \left( {\vec {r}} \right)} \right]} {\delta \rho \left( {\vec {r}} \right)}}} \right. \kern-0em} {\delta \rho \left( {\vec {r}} \right)}}} \right|}_{{\rho = {{\rho }^{{\left( {\text{e}} \right)}}}}}} = 0$ на равновесный профиль плотности ${{\rho }^{{\left( {\text{e}} \right)}}}\left( r \right)$ приводит к интегральному уравнению

где – химический потенциал системы твердых сфер. Интегральное уравнение (6) можно решать итерациями [34–36].

Из сравнения выражений (1) и (5) видим, что в градиентном методе функционала плотности интеграл $\frac{1}{2}\int d \vec {r}\int d \vec {r}{\kern 1pt} 'w(\left| {\vec {r} - \vec {r}{\kern 1pt} '} \right|)\rho \left( {\vec {r}} \right)\rho \left( {\vec {r}{\kern 1pt} '} \right)$ из (5) заменяется на интеграл $\int {\left( { - a{{\rho }^{2}} + \frac{C}{2}{{{(\nabla \rho )}}^{2}}} \right)} d\vec {r}$. Явный вид потенциала взаимодействия молекул флюида $w$ в градиентном методе не фигурирует, он входит в уравнения только посредством параметров $a$ и $C$. Как следует из сравнения интегралов $\frac{1}{2}\int d \vec {r}\int d \vec {r}{\kern 1pt} 'w(\left| {\vec {r} - \vec {r}{\kern 1pt} '} \right|)\rho \left( {\vec {r}} \right)\rho \left( {\vec {r}{\kern 1pt} '} \right)$ и $\int {\left( { - a{{\rho }^{2}} + \frac{C}{2}{{{(\nabla \rho )}}^{2}}} \right)} d\vec {r}$, для того, чтобы градиентный метод правильно описывал объемную фазу, параметр $a$ должен быть связан с потенциалом $w$ следующим образом:

В [1–3] константы $a\,$ и $d$ были связаны с параметрами флюида в критической точке, а коэффициент $C$ – с поверхностным натяжением на плоской границе жидкость–пар. Таким образом, константы $a$ и $C$ были взяты как независимые параметры. Однако между ними существует известная связь [33] через соотношение

где ${{c}^{{(2)}}}(\rho ;r)$ – прямая двухчастичная корреляционная функция однородного флюида с плотностью $\rho $. Используя вытекающее из определения прямой двухчастичной корреляционной функции выражение где $F[\rho ]$ есть свободная энергия системы, принимая во внимание сферическую симметрию системы и учитывая, что $F[\rho ]$ равна сумме первого, второго и четвертого слагаемых в правой части (5), видим, что из (9) и (10) следует [40]

Таким образом, константы $a$ и $С$ связаны через второй и соответственно четвертый интегральные моменты дальнодействующего центрального потенциала.

Следуя [33, 35, 36], мы рассмотрели два модельных центральных потенциала $w(r)$. Первый потенциал есть потенциал Юкавы

где мы положили $\lambda = {1 \mathord{\left/ {\vphantom {1 d}} \right. \kern-0em} d}$, а параметр $\alpha $ выбрали так, чтобы интегральный метод можно было сравнивать с градиентным. Если в (12) положить $\alpha \equiv 2a$, то в соответствии с (12) находим $ - 2\pi \int_0^\infty {dr{{r}^{2}}{{w}_{{\text{Y}}}}\left( r \right)} = a$. При этом для потенциала Юкавы связь между параметрами $a$ и $С$ имеет совсем простой вид ${С \mathord{\left/ {\vphantom {С 2}} \right. \kern-0em} 2} = {a \mathord{\left/ {\vphantom {a {{{\lambda }^{2}}}}} \right. \kern-0em} {{{\lambda }^{2}}}} = a{{d}^{2}}$.

Как и в [1–3], получим значение $a$ из экспериментальных данных о критических параметрах флюида, но вычислим константу $С$ как $2a{{d}^{2}}$. Этот способ и оценка для $С$ из [1–3] дают близкие результаты: ${{2a{{d}^{2}}} \mathord{\left/ {\vphantom {{2a{{d}^{2}}} C}} \right. \kern-0em} C} \approx 1.07$. Заметим, что профили плотности в градиентном методе функционала плотности заметно зависят от выбора $С$. Для нахождения термодинамических характеристик пузырьков оценки $С$, взятые в [1–3], позволяет связать теорию с экспериментом безотносительно вида межмолекулярного потенциала. Но ниже мы при выбранном $\lambda = {1 \mathord{\left/ {\vphantom {1 d}} \right. \kern-0em} d}$ будем пользоваться “согласованным” значением $C = 2a{{d}^{2}}$.

Второй потенциал – это потенциал Леннард-Джонса в форме Викса–Чендлера–Андерсона [41]:

где ${{r}_{{\min }}} = {{2}^{{1/6}}}{{\sigma }_{{{\text{LJ}}}}}$, $\varepsilon \,$и ${{\sigma }_{{{\text{LJ}}}}}$– параметры потенциала Леннард-Джонса (${{\sigma }_{{{\text{LJ}}}}} \ne \sigma $). Опять-таки, в целях сравнения результатов, выберем [40] эти параметры такими, чтобы второй и четвертый моменты потенциала Леннард-Джонса совпадали с соответствующими моментами потенциала Юкавы

Отсюда получаем $\varepsilon = - {\alpha \mathord{\left/ {\vphantom {\alpha {B\sigma _{{{\text{LJ}}}}^{3}}}} \right. \kern-0em} {B\sigma _{{{\text{LJ}}}}^{3}}} \approx 0.3152{{\lambda }^{3}}\alpha $, ${{\sigma }_{{{\text{LJ}}}}} = {{\lambda }^{{ - 1}}}\sqrt {{{6B} \mathord{\left/ {\vphantom {{6B} A}} \right. \kern-0em} A}} \approx 0.5856{{\lambda }^{{ - 1}}}$. В силу (8) и (11) равенство правых частей (14) и (15) обеспечивают идентичность потенциалов для градиентного приближения метода функционала плотности.

Заметим теперь, что в выражении (8) для параметра $a$ интегрирование ведется по всему объему системы. В случае образования паровой прослойки вокруг лиофобной частицы это вносит ощутимую ошибку, влияние которой мы заметили в разделе 1 при использовании метода упругой ленты. Действительно, используя параметр $a$ в градиентном разложении, мы включаем взаимодействие молекул флюида в точке $\vec {r}$ с молекулами флюида, которые находятся в объеме, занимаемом твердой частицей (поскольку интегрирование межчастичного потенциала $w$ в (8) ведется, в том числе, по объему, занимаемому частицей). При этом взаимодействие с молекулами твердого ядра уже учтено слагаемым $\int_V {\rho {{w}_{{{\text{pf}}}}}(r)d\vec {r}} $ в (1). Это достаточно сильно влияет на величину ${{\Omega }^{{{\text{pf}}}}}$, однако на профиль плотности почти не влияет, так как определяющую роль в уравнении (3) играет факт наличия расходимости при $r = {{R}_{{\text{p}}}}$, т.е. отталкивающая часть потенциала ${{w}_{{{\text{pf}}}}}(r)$, и коэффициент ${{\rho }_{{\text{p}}}}{{\varepsilon }_{{{\text{pf}}}}}$ при ней; на отталкивающую часть ${{w}_{{{\text{pf}}}}}(r)$ такая “лишняя добавка межмолекулярного взаимодействия” не влияет. Притягивающая же часть ${{w}_{{{\text{pf}}}}}(r)$ очень мала в случае лиофобной частицы. Также отметим, что притягивающая часть ${{w}_{{{\text{pf}}}}}(r)$ играет роль на больших расстояниях от частицы, где приближение среднего поля более оправданно, а отталкивающая – на малых расстояниях. Это обстоятельство, во-первых, объясняет “аномальное” значение ${{\Omega }^{{{\text{pf}}}}}$ для первой картинки $\rho (r) = {{\rho }^{{\text{L}}}}$ в методе упругой ленты (где плотность флюида высока вблизи частицы) и, во-вторых, позволяет надеяться на малую погрешность ${{\Omega }^{{{\text{pf}}}}}$ для остальных картинок (где плотность мала вблизи частицы).

Заметим теперь, что в случае нуклеации капельки на лиофильной частице лишнее интегрирование по объему частицы лишь немного увеличило бы и без того большой энергетический параметр ${{\varepsilon }_{{{\text{pf}}}}}$ взаимодействия с лиофильной частицей и поэтому мало повлияло бы на результат. Кроме того, в случае нуклеации капельки на лиофильной частице в методе упругой ленты первой картинкой был бы профиль $\rho (r) = {{\rho }^{{\text{G}}}} \ll {{\rho }^{{\text{L}}}}$ с малой плотностью, поэтому абсолютное значение ошибки в случае нуклеации капельки незаметно по сравнению с погрешностью ${{\Omega }^{{{\text{pf}}}}}$ для профиля $\rho (r) = {{\rho }^{{\text{L}}}}$ в случае нуклеации пузырька вокруг лиофобной частицы.

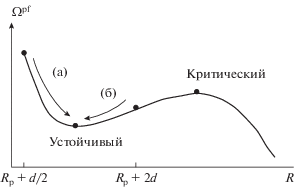
Рассмотрим итерационное решение уравнения (6) для пузырька вокруг лиофобной частицы. При поиске профиля плотности в седловой точке функционала (5) в качестве нулевого приближения брался профиль-ступенька, отвечающий пузырьку с радиусом ${{r}_{{\text{c}}}} = \frac{{2\gamma _{\infty }^{{{\text{GL}}}}}}{{p\left( {{{\mu }_{\infty }}} \right)\left( {{{e}^{{\frac{{\mu - {{\mu }_{\infty }}}}{{{{k}_{{\text{B}}}}T}}}}} - 1} \right) - {{\rho }^{{\text{L}}}}\left( {{{\mu }_{\infty }}} \right)\left( {\mu - {{\mu }_{\infty }}} \right)}}$ (капиллярное приближение по формуле (2.7) из [3]), где $p\left( {{{\mu }_{\infty }}} \right)$ – давление флюида при ${{\mu }_{\infty }}$. Дальнейшая процедура описана в [35, 36]. Поиск минимума ${{\Omega }^{{{\text{pf}}}}}$ проходил намного проще, чем поиск седловой точки, так как система с увеличением числа итераций стремится прийти в искомый минимум. Для поиска профиля плотности устойчивого пузырька, ввиду его небольшого радиуса, был использован анзац в виде однородной жидкости вне сферы радиусом ${{R}_{{\text{p}}}} + {d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}$. Чтобы убедиться, что состояние в минимуме ${{\Omega }^{{{\text{pf}}}}}$ действительно устойчиво, мы использовали также анзац с радиусом ${{R}_{{\text{p}}}} + 2d$. В итоге итерационной процедуры были получены одинаковые профили плотности. Эволюция состояния системы в процессе проведения итераций с такими анзацами схематично показана стрелками на рис. 3.

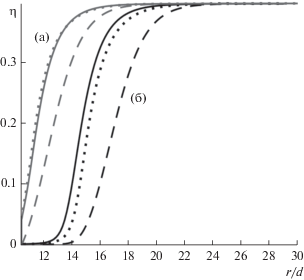
Результаты расчетов в сравнении с профилями, полученными в [1] как решения дифференциального уравнения (3) в градиентном методе функционала плотности, приведены на рис. 4. Видим, что градиентное приближение завышает радиус пузырька и делает его профиль более пологим. Профили критических паровых прослоек практически не отличаются от профилей гомогенных пузырьков. Это объясняется короткодействием потенциала взаимодействия с частицей. Профили устойчивых прослоек из интегрального метода не достигают нуля при $r = {{R}_{{\text{p}}}} + {d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}$, как это происходит в градиентном методе. Такое различие было замечено в [26] при рассмотрении флюида вблизи плоской стенки, обладающей только бесконечно большим отталкивающим потенциалом.

ЗАКЛЮЧЕНИЕ

Большой термодинамический потенциал системы из сферической лиофобной твердой частицы и растянутой жидкости был исследован в рамках градиентного приближения с помощью метода упругой ленты и в рамках интегрального метода функционала молекулярной плотности. Полученные в результате этого исследования равновесные профили плотности флюида вокруг твердой частицы были сравнены с профилями, которые для такой же системы дает решение уравнения Эйлера для градиентного метода функционала плотности.

Форма найденного пути минимального перепада энергии подтверждает наличие минимума большого термодинамического потенциала, то есть существование стабильных паровых прослоек в случае гетерогенной нуклеации. Профили плотности, полученные двумя способами (как численные решения дифференциального уравнения на точки стационарности функционала и как экстремумы пути минимального перепада энергии) практически совпадают, в том числе и на границе с твердой частицей.

Для двух моделей дальнодействующего межмолекулярного потенциала (Юкавы и Леннард-Джонса) были найдены профили плотности системы в рамках интегрального метода функционала плотности. Было обнаружено заметное количественное различие в толщинах пузырьков вокруг лиофобных частиц по сравнению с градиентным методом. Однако устойчивые паровые прослойки, соответствующие минимуму большого термодинамического потенциала системы, были обнаружены в рамках интегрального метода для обеих моделей.

Таким образом, нами были получены ответы на все вопросы, сформулированные во Введении.