Коллоидный журнал, 2021, T. 83, № 5, стр. 512-523
Закономерности протекания процессов коагуляции в полидисперсном нанозоле оксида циркония
А. В. Волкова 1, *, Д. А. Вдовиченко 1, Е. В. Голикова 1, Л. Э. Ермакова 1
1 Санкт-Петербургский государственный университет
199034 Санкт-Петербург, Университетская наб., 7-9, Россия
* E-mail: anna.volkova@spbu.ru
Поступила в редакцию 27.04.2021
После доработки 05.05.2021
Принята к публикации 12.05.2021
Аннотация
Методами турбидиметрии и динамического рассеяния света исследована агрегативная устойчивость полидисперсного золя оксида циркония со средним размером первичных частиц 24 нм и агрегатов 95 нм в широкой области концентраций хлорида натрия (3 × 10−3–1 М). Исследования проводили при значениях pH 4.2 и 5.6, когда частицы золя заряжены положительно, и при pH 11, когда они заряжены отрицательно. Определены и охарактеризованы зоны слабой и интенсивной медленной коагуляции, а также быстрой коагуляции золя. Показано, что пороги интенсивной медленной коагуляции, определенные из концентрационных зависимостей оптической плотности и среднего размера частиц, в большинстве случаев совпадают в пределах погрешности эксперимента. Высказаны предположения о механизме коагуляции и его изменении при переходе из одной зоны в другую, а также о роли соотношения размеров частиц отдельных фракций и их количеств в золе.
ВВЕДЕНИЕ
Реальные природные и промышленные дисперсные системы преимущественно являются полидисперсными. Это обстоятельство в значительной мере проявляется в процессах коагуляции и гетерокоагуляции золей и суспензий. Согласно классическим представлениям при перикинетической коагуляции предельным случаем неустойчивости коллоидного раствора является протекание процесса быстрой коагуляции, при котором каждое столкновение приводит к прочному соединению частиц, а скорость процесса определяется только их броуновским движением [1–3]. После достижения порога быстрой коагуляции, т.е. такой концентрации электролита, при которой энергетический барьер, препятствующий слипанию частиц, отсутствует, дальнейшее увеличение концентрации электролита (если речь не идет о специфически адсорбирующихся ионах в условиях сверхэквивалентной адсорбции, приводящей к изменению знака потенциала в плоскости наибольшего приближения и электрокинетического потенциала) уже не оказывает влияния на скорость коагуляции частиц [1–3]. Теоретический анализ процесса быстрой коагуляции был проведен Смолуховским [1, 2]. Согласно его представлениям, коллоидные частицы, сближаясь на некоторое расстояние R (радиус взаимодействия частиц), необратимо слипаются, т.е. вместо рассмотрения сил Ван-дер-Ваальса вводится представление о бесконечно глубокой потенциальной яме с вертикальной стенкой.
Через несколько лет после создания теории быстрой коагуляции монодисперсных систем Мюллером была предпринята попытка рассмотрения быстрой коагуляции полидисперсных систем. Мюллер учел то, что предположение Смолуховского о равновероятности столкновений между частицами разного и одинакового размеров является не вполне обоснованным [4, 5]. Согласно Мюллеру, для двух частиц различающегося радиуса, в особенности при сильном отличии их формы от сферической, вероятность столкновения значительно выше, чем для частиц одного размера. Это положение теории было подтверждено, в частности, опытами Вигнера и Маршалла по исследованию коагуляции золей пятиокиси ванадия и бензопурпурина [6], в которых наблюдалось пятидесятикратное превышение скорости быстрой коагуляции по сравнению с рассчитанной по Смолуховскому. Из совместного анализа теорий Смолуховского и Мюллера следует, что в двухкомпонентной дисперсной системе, содержащей различающиеся по размеру исходные частицы (с радиусами r01 и r02), скорость коагуляции $v$ должна быть выше рассчитанной по теории Смолуховского ($v$Sm) для монодисперсного золя.
Коагуляция полидисперсных систем исследовалась теоретически и экспериментально в работах Фридлендера [7–9], Регги и Мелика [10] и Ли [11, 12], в которых также было установлено, что скорость коагуляции в полидисперсных системах выше, чем в монодисперсных. В работах Ли было показано [11, 12], что при коагуляции изменение распределения частиц по размеру во времени может быть описано нелинейным интегро-дифференциальным уравнением, которое не имеет строгого аналитического решения. Аналитические решения этого уравнения были получены либо при допущении упрощенных представлений о ядре коагуляции, либо в асимптотическом виде. В работе [11] Ли, исходя из условия, что первоначальное распределение частиц по размеру в золе может быть представлено логнормальной функцией, описал функции распределения частиц некоторого объема по размерам и изменения полного числа частиц полидисперсного золя во времени.
В упомянутых выше теоретических работах авторы полагали, что коагуляция протекает необратимо, т.е. в основе рассмотрения лежала модель диффузионно-контролируемой агрегации (diffusion-limited cluster aggregation). В полидисперсной системе этот механизм коагуляции может иметь место при достаточно высокой концентрации электролита. Однако в области меньших концентраций велика вероятность того, что для относительно крупных частиц будет реализована другая модель – модель кинетически-контролируемой агрегации (reaction limited cluster aggregation). Эти две модели соответствуют разным межчастичным потенциалам: глубокому первичному энергетическому минимуму в отсутствие барьера в первом случае и наличию энергетического барьера перед таким минимумом – во втором. Это, в свою очередь, может обусловливать появление нескольких порогов коагуляции. В реальных полидисперсных системах коагуляция ансамбля частиц может быть осложнена еще и тем, что частицы могут образовывать относительно непрочные (в некоторых случаях легко распадающиеся) агрегаты во вторичном или ограниченном первичном минимумах на зависимостях энергии парного взаимодействия частиц от расстояния между ними.
Исследование и разработка математических методов решения кинетических уравнений, описывающих эволюцию функции распределения частиц по массам при заданной вероятности их столкновения и слипания, входит в круг задач макрокинетической теории коагуляции. В настоящее время имеется большое число теоретических работ, посвященных изучению кинетики агрегации частиц, среди которых особого внимания заслуживают работы [10, 13–22].
Экспериментальные исследования кинетики коагуляции коллоидных систем с относительно низкой исходной полидисперсностью показали, что процесс коагуляции протекает, как правило, ступенчато. С ростом концентрации электролита и времени наблюдения полидисперсность золя заметным образом возрастала [23–26]. Однако следует отметить, что в литературе имеется мало работ, посвященных детальному изучению устойчивости полидисперсных систем, в которых найденные пороговые значения концентрации электролита, т.е. границы различных зон коагуляции, трактовались бы с учетом дискретного спектра размеров частиц. В связи с этим очевидна необходимость развития представлений о коагуляции в реальных полидисперсных системах, в частности, в золях, полученных на основе воздушно-сухих нанопорошков. Это тем более важно, что области практического применения нанодисперсий находятся в стадии активного формирования.
Оксид циркония – это материал, которому уделяется все больше внимания благодаря его выдающимся механическим свойствам. ZrO2 может быть использован как адсорбент, катализатор, ионообменник. Большой интерес к нанокерамике на основе ZrO2 связан с ее высокими эксплуатационными характеристиками – механической прочностью, химической и термической стойкостью, антибактериальной активностью, биосовместимостью и др. [27–31].
Цель настоящей работы заключалась в проведении детального исследования устойчивости и коагуляции золя ZrO2 в растворах NaCl при различных значениях pH методами турбидиметрии и динамического рассеяния света, направленного на выявление влияния исходной полидисперсности золя на особенности его коагуляции.
ОБЪЕКТЫ И МЕТОДЫ ИССЛЕДОВАНИЯ
В качестве объекта исследования был выбран исходно агрегативно и седиментационно устойчивый гидрозоль оксида циркония, приготовленный на основе коммерческого нанопорошка ZrO2 (Вектон, Россия). Величина удельной поверхности Sуд порошка, определенная методом БЭТ по тепловой десорбции азота с хроматографической регистрацией, составила 44 м2/г. Средний размер первичных наночастиц d0, вычисленный по формуле
(1)
${{d}_{0}} = {6 \mathord{\left/ {\vphantom {6 {{{\rho }}{{S}_{{{\text{уд}}}}}}}} \right. \kern-0em} {{{\rho }}{{S}_{{{\text{уд}}}}}}},$Исходный порошок ZrO2 был трижды очищен методом электродиализа с сушкой оксида между циклами (после полного упаривания воды при температуре не выше 80°C оксид циркония сушили в течение 1 ч сначала при температуре 120°C, затем при 200°C). Об эффективности этого процесса судили по изменению положения изоэлектрической точки (ИЭТ) оксида циркония. Последовательная очистка коммерческого порошка ZrO2 методом электродиализа привела к смещению положения ИЭТ на фоне 10–2 М раствора хлорида натрия (рис. 1) от pH 6.5 для однократно очищенного порошка до pH 6.1 для оксида после двукратной очистки. Увеличение числа циклов электродиализа до трех не привело к заметным изменениям как величины электрокинетического потенциала, так и положения ИЭТ, что свидетельствует о полноте очистки поверхности оксида. Таким образом, ИЭТ исследуемого порошка ZrO2 находится при pH 6.1. Это значение попадает в интервал значений, приводимых для этого оксида в литературе [32]. Для дальнейшего исследования устойчивости и коагуляции золя оксида циркония был выбран порошок, подвергнутый трехкратной очистке.
Рис. 1.
Зависимости электрофоретической подвижности (Ue) и электрокинетического потенциала (ζS) частиц оксида циркония, очищенных методом электродиализа, от pH на фоне 10–2 М раствора NaCl.
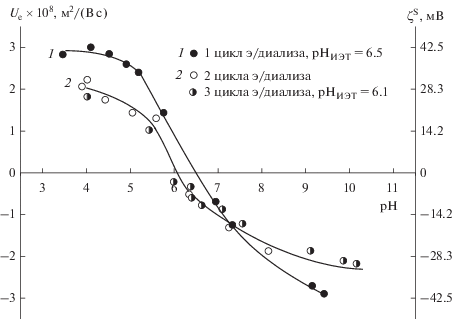
Агрегативно и седиментационно устойчивый гидрозоль оксида циркония был приготовлен из его водной суспензии с концентрацией 0.01 мас. %. Для этого очищенный порошок оксида диспергировали в воде в течение трех часов на ультразвуковой ванне марки “РЭЛТЕК” УЗВ-7/100-ТНМ при частоте 60 кГц, затем полученную 0.01%-ную дисперсию длительно отстаивали (в течение примерно двух недель), отбирали верхнюю (наиболее тонкодисперсную) фракцию и разбавляли ее деионизованной водой. Оптическая плотность полученного таким образом золя составила 0.378 ± 0.005.
В ходе работы изучали влияние pH (при его естественном значении 5.6 без добавок растворов кислоты или щелочи и при значениях pH 4.2 и 11) и концентрации фонового электролита NaCl (3 × 10–3–1 М) на агрегативную устойчивость разбавленного гидрозоля ZrO2. Для изучения агрегативной устойчивости гидрозоля использовались методы турбидиметрии, основанной на измерении зависимости оптической плотности D системы от времени, и динамического рассеяния света (ДРС).
Турбидиметрическое исследование проводили с помощью фотоэлектроколориметра КФК-3-01 в кювете длиной 5 см и шириной 2 см при длине волны 380 нм, соответствующей максимуму поглощения. Раствором сравнения служила деионизированная вода. Для получения дисперсий с необходимой концентрацией коагулянта смешивали равные объемы полученного устойчивого золя и раствора электролита удвоенной концентрации либо (в отсутствие электролита) деионизированной воды при помощи поршневого смесителя. Смешение происходило во встречных потоках в Т-образном канале, из которого смесь подавалась непосредственно в измерительную кювету. За точку отсчета принимали момент смешения золя с электролитом. Измерения проводили в течение 15 мин. На основании полученных данных были построены зависимости оптической плотности D от времени t. Значение pH среды изменяли путем добавления различных объемов 0.1 М растворов HCl или NaOH в воду или в раствор фонового электролита перед их добавлением к дисперсии оксида циркония. При нулевой концентрации соли при всех значениях pH величины оптической плотности были постоянны в течение всего времени эксперимента.
По окончании измерений оптической плотности при фиксированной концентрации электролита, а именно примерно через 20 мин после смешения золя с раствором хлорида натрия, были определены размеры и значения электрокинетического потенциала частиц ZrO2. Распределение частиц по размерам (РЧР) в образцах исследуемого золя, их средний размер и электрофоретическую подвижность (Ue) при различных значениях pH и концентрации электролита определяли на анализаторе Zetasizer Nano ZS (Malvern Instruments, Великобритания) методами ДРС (угол детектирования 173°) и лазерного допплеровского электрофореза соответственно. Образцы золя предварительно термостатировали 2 мин при 20°C в универсальной капиллярной U-образной кювете (DTS1070) с интегрированными позолоченными электродами. Погрешность определения значений Ue составила ±(0.1–0.2) м2/(В с). Электрокинетический потенциал (ζS) рассчитывали по уравнению Смолуховского
(2)
${{\zeta }^{{\text{S}}}} = \frac{{{\eta }}}{{{{\varepsilon }}{{{{\varepsilon }}}_{{\text{0}}}}}}{{U}_{{\text{e}}}},$Из экспериментально найденных значений электрофоретической подвижности для наименьших значений электрокинетического радиуса kа (где k – параметр Дебая, а – радиус первичной частицы, равный 12 нм) с учетом поляризации двойного электрического слоя были также рассчитаны значения электрокинетического потенциала в рамках модели Овербека–Буса–Вирсемы [33] (ζW).
Оптическая плотность исследуемого в работе гидрозоля оксида циркония, полученного разбавлением золя с оптической плотностью 0.378 ± ± 0.005 в два раза, составила 0.189 ± 0.005. Размер и морфология частиц золя ZrO2 были определены также методом сканирующей электронной микроскопии (СЭМ) на приборе Zeiss Merlin. Представленные на рис. 2 микрофотографии свидетельствуют о том, что золь является полидисперсным и в нем содержатся как отдельные (первичные) частицы с наиболее вероятным размером, близким к величине d0 = 24 нм, так и их (первичные) агрегаты с формой, близкой к сферической, и размером преимущественно 40–120 нм.
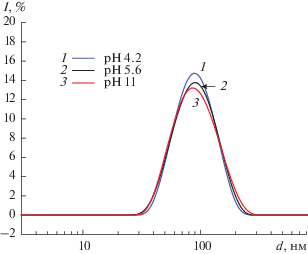
Результаты, полученные методом ДРС, согласуются с данными СЭМ. Исходный седиментационно и агрегативно устойчивый золь ZrO2 характеризуется достаточно узким РЧР (рис. 3): индекс полидисперсности PdI = 0.13, средний размер первичных агрегатов $d_{{{\text{0I}}}}^{{{\text{агр}}}}$, определенный из распределения интенсивности по размеру составил 95 нм, диапазон размеров частиц 32–220 нм. Однако следует отметить, что метод ДРС в нашем случае не дает информации о частицах размером меньше 30 нм, т.е. о первичных частицах, согласно данным СЭМ содержащихся в золе в достаточно большом количестве (рис. 2). Отметим также, что РЧР, полученные при исследуемых значениях pH, близки между собой.
Рис. 3.
Зависимости интенсивности рассеянного света от размера частиц в исходном седиментационно и агрегативно устойчивом золе ZrO2 при значениях pH 4.2 (1), 5.6 (2) и 11 (3).
С помощью лазерной поточной ультрамикроскопии [34] была определена численная концентрация регистрируемых данным методом частиц золя, т.е. относительно крупных агрегатов, которая составила 1.2 × 108 см–3.
Для приготовления растворов и дисперсий использовали деионизированную воду, удельная электропроводность которой не превышала 1.5 × 10–6 Ом–1 см–1 (система очистки воды Аквалаб AL Plus). pH среды определяли на pH-метре SevenMulti (Mettler Toledo).
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Результаты турбидиметрического изучения агрегативной устойчивости золя ZrO2 в растворах NaCl при pH 5.6, когда его частицы заряжены положительно, приведены на рис. 4. Анализ зависимостей оптической плотности золя от времени при его естественном значении pH показал, что ход кривых D(t) в интервале концентраций электролита 3 × 10–3 М < CNaCl ≤ 2 × 10–2 М характерен для медленной коагуляции (МК), а при CNaCl > 2 × × 10–2 М – для быстрой коагуляции (БК).
Рис. 4.
Зависимости оптической плотности гидрозоля ZrO2 с положительно заряженными частицами от времени наблюдения при естественном значении pH 5.6 и разной концентрации NaCl.
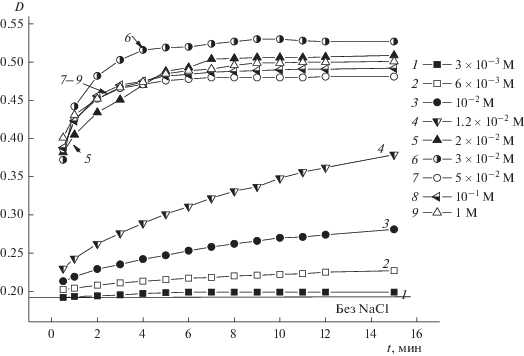
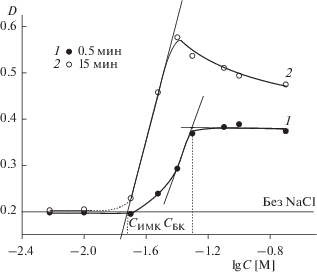
Как было показано в работе [24], для полидисперсных золей оксидов интенсивность процесса МК в зависимости от концентрации электролита может различаться, что обуславливает появление зон слабой и интенсивной МК. С учетом этого факта точные значения порогов коагуляции были определены путем построения зависимостей оптической плотности гидрозоля от концентрации раствора соли при фиксированном времени наблюдения (рис. 5). Порог быстрой коагуляции (CБК) находился при малом времени наблюдения (t = 0.5 мин, рис. 5, кривая 1) путем экстраполяции линейного участка зависимости D–lgC, для которого характерны максимальные значения dD/dC, на линию, соответствующую постоянным значениям оптической плотности при высоких концентрациях фонового электролита. При максимальном времени наблюдения (t = 15 мин, рис. 5, кривая 2) экстраполяция линейного участка зависимости D–lgC на линию устойчивости золя позволила точно определить порог интенсивной МК (CИМК).
Рис. 5.
Зависимости оптической плотности гидрозоля ZrO2 с положительно заряженными частицами от концентрации NaCl при 0.5 (1) и 15 мин (2) наблюдения и естественном значении pH 5.6. I – зона устойчивости, II – зона слабой медленной коагуляции, III – зона интенсивной медленной коагуляции, IV – зона быстрой коагуляции.
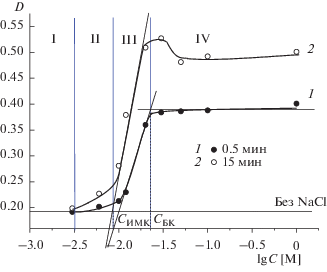
Графически определенные при pH 5.6 пороги интенсивной медленной и быстрой коагуляции составили 8.5 × 10–3 М и 2.3 × 10–2 М соответственно (рис. 5, табл. 1). Для порога слабой МК (CСМК) по имеющимся экспериментальным данным достоверно удалось определить лишь область возможных концентраций электролита: 3 × 10–3 М < CСМК ≤ 6 × 10–3 М. Следует отметить, что при естественном значении pH золя пороговые значения концентрации NaCl являются достаточно малыми. Пороги коагуляции золя ZrO2 при значениях pH 4.2 и 11 были определены аналогичным образом, и результаты представлены в табл. 1.
Таблица 1.
Результаты определения экспериментальных порогов коагуляции золя ZrO2 при различных значениях pH дисперсионной среды
| pH | Знак заряда частиц |
ССМК и СИМК (М) из кривых D–lgC |
СИМК, М | СБК, М | ||
|---|---|---|---|---|---|---|
| из кривых dI–lgC |
из кривых dV–lgC |
из кривых dN–lgC |
из кривых D–lgC |
|||
| 4.2 | + | 3 × 10–2 < ССМК ≤ 5 × 10−2, СИМК = 6.8 × 10–2 |
6.9 × 10–2 | 6.9 × 10–2 | 8.1 × 10–2 | >10–1 |
| 5.6 | + | 3 × 10–3 < ССМК ≤ 6 × 10–3, СИМК = 8.5 × 10–3 |
9.3 × 10–3 | 9.5 × 10–3 | 9.7 × 10–3 | 2.3 × 10–2 |
| 11 | – | СИМК = 2 × 10−2 | 2.0 × 10–2 | 2.2 × 10–2 | 2.7 × 10–2 | 5.0 × 10–2 |
Анализ зависимостей оптической плотности золя ZrO2 от времени при pH 4.2, когда его частицы также заряжены положительно, показал (рис. 6), что система устойчива при CNaCl ≤ 3 × 10–2 М, в интервале концентраций 3 × 10–2 М < CNaCl ≤ ≤ 1 × 10–1 М протекает МК, а при концентрации раствора электролита > 10–1 М – БК. Графически определенное значение порога интенсивной МК (CИМК) составило 6.8 × 10–2 М (табл. 1).
Рис. 6.
Зависимости оптической плотности гидрозоля ZrO2 с положительно заряженными частицами от времени наблюдения при pH 4.2 и концентрации N-aCl 10–2 (1), 2 × 10–2 (2), 3 × 10–2 (3), 5 × 10–2 (4), 8 × 10–2 (5), 10–2 М (6).

Пороги БК и слабой МК по имеющимся экспериментальным данным точно определить не удалось: CБК > 10–1 М и 3 × 10–2 М < CСМК ≤ 5 × 10–2 М. Следует отметить, что пороговые значения концентрации NaCl при pH 4.2 практически на порядок выше соответствующих значений при естественном значении pH золя. Это, по-видимому, связано с ростом вклада сил ионно-электростатического отталкивания в суммарную энергию парного взаимодействия частиц за счет более высоких значений их электрокинетического потенциала при кислом значении pH. Действительно, анализ результатов определения дзета-потенциала частиц оксида циркония свидетельствует о том, что при постоянной концентрации раствора электролита значения электрокинетического потенциала при pH 4.2 выше, чем при pH 5.6 (рис. 7).
Рис. 7.
Зависимости электрокинетического потенциала (ζW) частиц оксида циркония от концентрации растворов NaCl при значениях pH 4.2 (1), 5.6 (2) и 11 (3).

Анализ зависимостей оптической плотности золя ZrO2 от времени при pH 11, когда его частицы заряжены отрицательно, показал (рис. 8), что система устойчива при CNaCl ≤ 10–2 М, при концентрации хлорида натрия 2 × 10–2 М уже наблюдается МК, а при CNaCl ≥ 5 × 10–2 М – БК.
Рис. 8.
Зависимости оптической плотности гидрозоля ZrO2 с отрицательно заряженными частицами от времени наблюдения при pH 11 и концентрации NaCl 6 × 10–3 (1), 10–2 (2), 2 × 10–2 (3), 3 × 10–2 (4), 4 × 10–2 (5), 5 × 10–2 (6), 8 × 10–2 (7), 10–1 (8), 2 × 10–1 М (9).
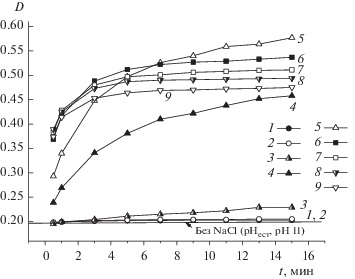
Как видно на рис. 9 (кривая 2), для золя отрицательно заряженных частиц зона слабой МК либо отсутствует, либо характеризуется очень узким концентрационным интервалом: 10–2 < CСМК < < 2 × 10–2 М. Графически определенные пороги интенсивной МК и БК составили 2 × 10–2 М и 5.0 × 10–2 М соответственно (рис. 9, табл. 1). Пороговые концентрации NaCl при pH 11 выше таковых при естественном значении pH золя (см. табл. 1), что обусловлено различием в абсолютных значениях дзета-потенциала частиц оксида циркония. Следует отметить, что, несмотря на более высокие абсолютные значения ζW-потенциала частиц в щелочной области pH по сравнению с кислой областью практически во всем концентрационном интервале (рис. 7), при pH 4.2 золь ZrO2 значительно более устойчив.
Рис. 9.
Зависимости оптической плотности гидрозоля ZrO2 с отрицательно заряженными частицами от концентрации NaCl при pH 11 и времени наблюдения 0.5 (1) и 15 мин (2).
Зависимости среднего размера частиц ZrO2, определенного методом ДРС через 20 мин после добавления к золю раствора электролита, от концентрации хлорида натрия представлены на рис. 10−12. Отметим, что в ряде случаев, что особенно характерно для области интенсивной МК, наблюдалось появление двух пиков на кривых РЧР. На графиках соответствующие им значения соединены пунктирными линиями и приведены процентные доли соответствующего параметра для частиц данного размера.
Рис. 10.
Зависимости среднего размера частиц dI гидрозоля ZrO2, определенного из распределения интенсивности рассеянного света по размеру частиц, от концентрации NaCl при значениях pH 5.6 (1), 11 (2) и 4.2 (3) и времени наблюдения 20 мин.
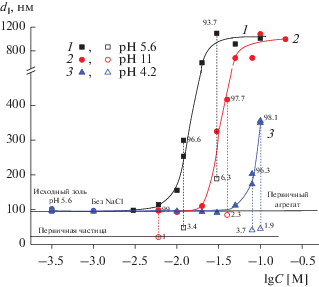
Из рис. 10−12 следует, что по мере увеличения концентрации NaCl и нарушения агрегативной устойчивости золя возрастает средний размер частиц ZrO2, причем в случае pH 5.6 и 11 вплоть до близких значений d, в среднем в 10–20 раз превышающих размер первичных агрегатов в исходном золе.
По полученным зависимостям, проведенным через точки, соответствующие большему значению среднего размера частиц в случае бимодального РЧР, методом экстраполяции, аналогичным описанному выше для зависимостей D–lgC при t = 15 мин, были также графически определены пороги интенсивной МК. Результаты представлены в табл. 1. Отметим, что анализ концентрационных зависимостей среднего размера частиц ZrO2 при pH 11 (рис. 10−12, кривые 2) показал, что, по-видимому, во всей области МК скорость изменения размера частиц практически постоянна, и, следовательно, в ней протекает только интенсивная МК, что согласуется с данными турбидиметрии (рис. 9, кривая 2).
Как следует из данных, приведенных в табл. 1, значения CИМК, найденные из концентрационных зависимостей оптической плотности и среднего размера частиц, совпадают в пределах погрешности, за исключением таковых, полученных из зависимостей dN–lgC при pH 4.2 и 11. В последнем случае область слабой МК практически отсутствует, и при pH 4.2 (рис. 12, кривая 3) величины CИМК несколько превышают таковые, определенные из зависимостей D(dI, dV)–lgC, особенно в кислой области pH. Возможно, это связано с тем, что при добавлении растворов кислоты или щелочи вследствие возрастания абсолютной величины дзета-потенциала происходит распад части агрегатов, содержащихся в исходно устойчивом гидрозоле при естественном значении pH. Это приводит, наряду с уменьшением содержания достаточно крупных агрегатов, к увеличению численной концентрации мелких частиц (первичных частиц или агрегатов с размером меньше среднего при pH 5.6), а, следовательно, и к уменьшению доли медленно коагулирующих мелких частиц от их общего количества в дисперсии. Это, вероятно, и обуславливает близкие численные РЧР в области слабой МК и в начале области интенсивной МК. Изменением соотношений количеств и размеров частиц в системе можно объяснить и проявление второго пика с максимумом вблизи 20 нм (первичные частицы), который становится “видимым” на распределении интенсивности рассеяния по размеру (рис. 13а, кривая 1) для устойчивого гидрозоля при pH 11 и концентрации NaCl 6 × 10–3 М на фоне пика первичных агрегатов. При этом если вклад “мелких” частиц в интенсивность рассеянного света составляет 1% (рис. 13а, кривая 1), то их численная концентрация – 90.9% (рис. 13в, кривая 1). Это доказывает то, что в исходных золях с мономодальным РЧР помимо агрегатов первичных частиц присутствуют и они сами, что подтверждают и данные СЭМ (рис. 2), причем концентрация этих частиц, которые чаще всего “не видны” методом ДРС, весьма значительна и зависит от pH дисперсии. Этот факт, по-видимому, и обуславливает практическое отсутствие зоны слабой МК при значении pH 11, при котором абсолютное значение дзета-потенциала максимально (рис. 7), а, следовательно, максимальна и доля первичных частиц в исходном золе. Наличие в исходном устойчивом гидрозоле “мелких” частиц, несомненно, обуславливает необходимость учета их роли в устойчивости и коагуляции полидисперсных систем при их теоретическом описании.
Рис. 11.
Зависимости среднего размера частиц dV гидрозоля ZrO2, определенного из объемного распределения частиц по размеру, от концентрации NaCl при различных значениях pH и времени наблюдения 20 мин.
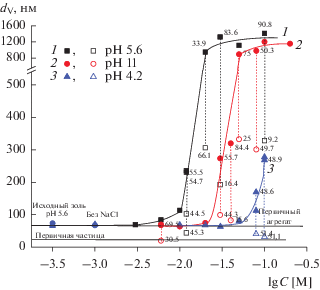
Рис. 12.
Зависимости среднего размера частиц dN гидрозоля ZrO2, определенного из распределения числа частиц по их размеру, от концентрации NaCl при различных значениях pH и времени наблюдения 20 мин.
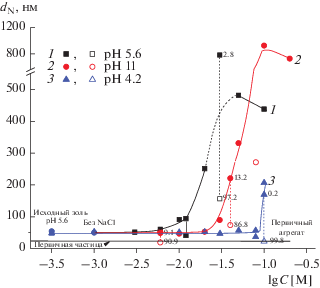
Рис. 13.
Зависимости (а) интенсивности рассеянного света, (б) объема и (в) числа частиц от их размера в золе ZrO2 при значениях pH 11 (1, 1') и 5.6 (2–8) и различной концентрации NaCl; t = 20 мин.

Полученные экспериментальные результаты позволяют сделать предположение о возможном ходе коагуляции в полидисперсном золе, содержащем как первичные частицы, так и агрегаты этих частиц. Для наглядности эволюции размеров частиц гидрозоля ZrO2 с увеличением концентрации раствора хлорида натрия на рис. 13 приведены распределения частиц по размерам при естественном значении pH.
Зона слабой МК характеризуется невысокой скоростью процесса (dD/dt), небольшим по сравнению с устойчивой дисперсией увеличением D даже при максимальном времени наблюдения, значений PdI (в пределах 0.01–0.02) и среднего размера частиц, сопровождающегося соответственно небольшим сдвигом РЧР в область бóльших размеров с ростом концентрации электролита (рис. 13, кривая 3). Это, по-видимому, свидетельствует о начале коагуляции “мелких” (первичных) частиц или их небольших агрегатов (соответствующих нижнему пределу на кривой РЧР).
Для зоны интенсивной МК характерно резкое по сравнению с областью слабой МК увеличение значений PdI (на 0.04–0.13), оптической плотности и среднего размера частиц (существенное смещение РЧР в область бóльших размеров (рис. 13, кривые 4, 5)), появление бимодального РЧР, а также практически линейный рост величин D и d, соответствующих крупной фракции частиц при бимодальном РЧР, с увеличением концентрации электролита (при t = const). Это может свидетельствовать о коагуляции всего ансамбля частиц золя, скорость и механизм протекания которой зависят как от концентрации раствора соли, так и от размеров частиц и содержания конкретных фракций в исходной дисперсии. При этом надо иметь в виду, что коагуляция крупных первичных агрегатов даже при незначительной их численной концентрации в золе может обуславливать достаточно выраженные изменения исследуемых параметров системы в связи с их высокой рассеивающей способностью (намного большей по сравнению с мелкими частицами). Обращает также на себя внимание тот факт, что в ряде случаев при больших временах наблюдения оптическая плотность золя в зоне интенсивной МК превышает таковую в зоне БК (рис. 4, 8). Это, возможно, связано с различием в структуре формирующихся агрегатов: для быстрой коагуляции характерно образование менее плотно упакованных агрегатов, обладающих, вследствие этого, меньшей рассеивающей способностью, что приводит, в свою очередь, к меньшим значениям D при концентрациях электролита выше порога БК.
Следует также отметить, что в области интенсивной МК в ряде случаев для золей с бимодальным РЧР наблюдалось, помимо увеличения среднего размера агрегатов по сравнению с устойчивой дисперсией, появление пика с максимумом при $d_{{}}^{{{\text{агр}}}}$ < $d_{{\text{0}}}^{{{\text{агр}}}}$ (рис. 10–12, кривые 1, 3) вплоть до размеров, близких к размеру первичных частиц (рис. 12, кривая 3). По-видимому, в условиях, когда скорость МК уже достаточно велика и средний размер частиц крупной фракции растет с одновременным уменьшением их числовой концентрации, происходит резкое изменение соотношений размеров количеств рассеивающих частиц в системе, и становятся “видимыми” и более мелкие частицы. Это свидетельствует о том, что, вероятнее всего, скорость коагуляции крупных частиц в указанных системах выше, чем небольших по размеру агрегатов или первичных частиц, и, следовательно, коагуляция протекает по безбарьерному механизму (в дальнем потенциальном минимуме). Однако для подтверждения этого предположения необходимо провести расчет энергии взаимодействия частиц в рамках теории ДЛФО. Отметим, что в области МК нельзя также исключать вероятность коагуляции первичных частиц и агрегатов между собой.
Для области БК при различных концентрациях NaCl в основном характерны близкие мономодальные РЧР (рис. 13, кривые 7, 8), близкие и существенно бóльшие значения PdI (в нашем случае примерно в 2 раза) и среднего размера частиц по сравнению с устойчивым золем. Следствием этого является постоянство оптической плотности при изменении концентрации электролита (рис. 5, кривая 2). Однако при концентрациях раствора соли, близких к пороговым значениям CБК, зона БК может также характеризоваться как мономодальным РЧР с максимумом, сдвинутым в область меньших размеров по сравнению с таковым при CNaCl$ \gg $ CБК, так и бимодальным РЧР, причем пик, характеризующий крупную фракцию, близок по положению к пику при СNaCl$ \gg $ CБК (рис. 13а, 13б, кривые 6–8 и рис. 10, 11, кривые 1, 2). По-видимому, это обстоятельство может обуславливать несколько бóльшие значения оптической плотности системы при концентрациях электролита, близких к CБК, чем при СNaCl$ \gg $ CБК, в случае далеко зашедшей коагуляции (рис. 5, кривая 2), тогда как при малых t величина D во всей области БК постоянна (рис. 5, кривая 1). Анализ наблюдаемых закономерностей позволяет предположить, что в начальной области БК частицы золя в зависимости от их размера, по-видимому, быстро коагулируют по различным механизмам – как по барьерному, так и безбарьерному. Следует отметить, что высказанные предположения, основанные на анализе экспериментальных данных, несомненно, могут стать более обоснованными после сопоставления полученных результатов с расчетами в рамках современных теорий устойчивости коллоидов.
ЗАКЛЮЧЕНИЕ
Агрегативная устойчивость полидисперсного золя диоксида циркония, содержащего как первичные частицы, так и их агрегаты, изучена методами турбидиметрии и динамического рассеяния света в растворах хлорида натрия с концентрацией 3 × 10–3–1 М при различных значениях pH (4.2, 5.6, 11). Графически определены пороги интенсивной медленной и быстрой коагуляции, обозначен диапазон концентраций начала слабой медленной коагуляции. Показано, что наибольшей устойчивостью золь обладает при pH 4.2, несмотря на более высокие абсолютные значения ζW-потенциала частиц при pH 11, а наименьшей – при естественном значении pH 5.6, что согласуется с результатами определения электрокинетического потенциала частиц ZrO2. Установлено также, что в исходном золе ZrO2 с мономодальным РЧР помимо агрегатов частиц присутствуют и сами первичные частицы, причем концентрация этих частиц, которые чаще всего “не видны” в спектрометре ДРС, весьма значительна и зависит от pH дисперсии.
Выявлены общие закономерности постадийной (ступенчатой) коагуляции полидисперсного золя ZrO2: обобщены основные характерные черты каждой из зон коагуляции, подчеркнута роль соотношения как размеров, так и численных концентраций частиц исходного полидисперсного золя в реализующемся механизме коагуляционного процесса и его влияния на тип формирующихся агрегатов. Высказано предположение, что в области слабой МК с наибольшей вероятностью коагулируют “мелкие” частицы ZrO2 – первичные частицы или небольшие их агрегаты (соответствующие нижнему пределу размеров на кривой РЧР для исходного золя), тогда как в области интенсивной МК, для которой характерно появление бимодального РЧР, по-видимому, коагулирует уже весь ансамбль частиц.
На основании анализа экспериментальных данных выдвинуто предположение о том, что как в области интенсивной МК, так и в начальной области БК частицы золя в зависимости от их размера могут коагулировать по различным механизмам – как по барьерному, так и безбарьерному, причем в области интенсивной МК как медленно, так и быстро, что находит свое отражение в характере РЧР. В области БК при концентрациях NaCl существенно выше пороговой весь ансамбль частиц золя быстро коагулирует по барьерному механизму.
Список литературы
Smoluchowski M. // Z. Phys. Chem. 1917. V. 92. P. 129.
Эйнштейн А., Смолуховский М. Броуновское движение. М.–Л.: ОНТИ, 1936.
Кройт Г.Р. Наука о коллоидах. Т. 1. М.: Изд-во иностр. лит-ры, 1955.
Müller H. // Kolloid-Z. 1926. V. 38. P. 1.
Müller H. // Kolloid Beihefte. 1928. V. 26. P. 257.
Wiegner G., Marshall C.E. // Z. Phys. Chem. 1929. A. V. 140. P. 39.
Wang C.S., Friedlander S.K. // J. Colloid Interface. Sci. 1967. V. 24. P. 170.
Swift D.L., Friedlander S.K // J. Colloid Interface. Sci. 1964. V. 19. P. 621.
Friedlander S.K. Smoke, Dust and Haze: Fundamentals of Aerosol Behavior. New York: Wiley, 1977.
Reggy S.R., Melik D.H., Fogler H.S. // J. Colloid Interface. Sci. 1981. V. 82. P. 116.
Lee K.W. // J. Colloid Interface. Sci. 1983. V. 92. P. 315.
Lee K.W., Chen H. // Aerosol Sci. Technol. 1984. V. 3. P. 327.
Hunt J.R. Coagulation in continuous particle size distribution; Theory and experimental verification. Report No. AC-5-80. California Institute of Technology, 1980.
Пеньков Н.В. Коагуляционные процессы в дисперсных системах. Екатеринбург: Издательство “Сократ”, 2006.
Волощук В.М., Седунов Ю.С. Процессы коагуляции в дисперсных системах. Л.: Гидрометеоиздат, 1975.
Elimelech M., Gregory J., Jia X., Williams R.A. Particle Deposition and Aggregation: Measurement, Modelling and Simulation. London: Butterworth-Heinemann, 2013.
Dubovski P.B. Mathematical Theory of Coagulation. Lecture Notes Series. V. 23. Seoul: Seoul National University, 1994.
Dubovski P.B. // J. Phys. A: Math. 1999. V. 32. P. 781.
Дубовский П.Б. // ЖЭТФ. 1999. Т. 116. С. 717.
Wu K.L., Lai S.K. // Langmuir. 2005. V. 21. P. 3238.
Wattis J.A.D. // Physica D: Nonlinear Phenomena. 2006. V. 222. P. 1.
Kinetic Aggregation and Gelation. Ed. by Family F., Landau D.P. Amsterdam: Elsevier, 1984.
Molina-Bolıvar J.A., Galisteo-Gonzalez F., Hidalgo-Alvarez R. // J. Colloid Interface Sci. 1997. V. 195. P. 289.
Volkova A.V., Ermakova L.E., Golikova E.V. // Colloids Surf. A. 2017. V. 516. P. 129.
Чернобережский Ю.М., Голикова Е.В. // Коллоид. журн. 1974. Т. 36. С. 115
Молодкина Л.М., Голикова Е.В., Бареева Р.С., Чусов А.Н., Богданова Н.Ф. // Коллоид. журн. 2016. Т. 78. С. 578.
Stevens R. Zirconia and Zirconia Ceramics. Magnesium Elektron Ltd. Pub. № 113, 1986.
Jia Y., Duran C., Hotta Y., Sato K., Watari K. // J. Colloid Interface Sci. 2005. V. 291. P. 292.
Danelska A., Ulkowska U., Socha R.P., Szafran M. // J. Eur. Ceram. Soc. 2013. V. 33. P. 1875.
Bowen P., Carry C. // Powder Technol. 2002. V. 128. P. 248.
Duran C., Jia Y., Hotta Y., Sato K., Watari K. // J. Mater. Res. 2005. V. 20. P. 1348.
Lyklema J. Fundamentals of Interface and Colloid Science. V. 2. San Diego: Academic Press, 2001.
Wiersema P.H., Loeb A.L., Overbeek J.Th.G. // J. Colloid Interface Sci. 1966. V. 22. P. 78.
Molodkina L.M., Golikova E.V., Chernoberezhsky Yu.M., Kolikov V.M. // Colloids Surf. A. 1995. V. 98. P. 1.
Дополнительные материалы отсутствуют.
Инструменты
Коллоидный журнал



